Wissen / Können

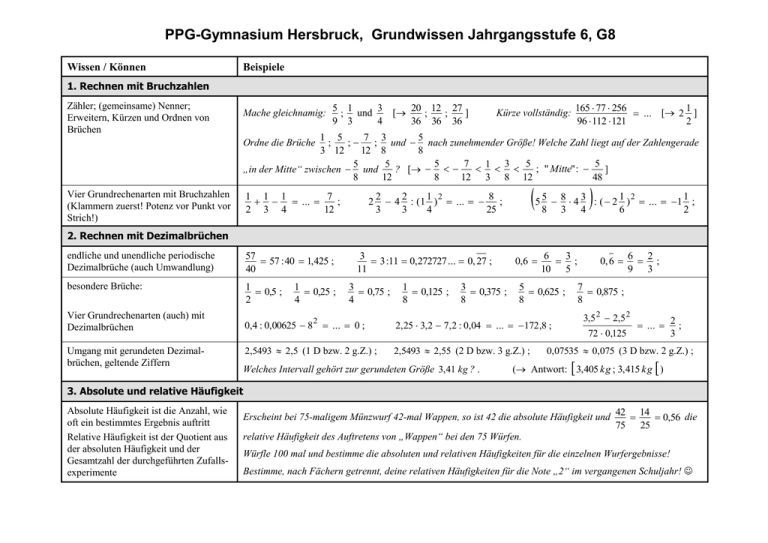
PPG-Gymnasium Hersbruck, Grundwissen Jahrgangsstufe 6, G8
Wissen / Können
Beispiele
1. Rechnen mit Bruchzahlen
Zähler; (gemeinsame) Nenner;
Erweitern, Kürzen und Ordnen von
Brüchen
Mache gleichnamig:
5 1 und 3 [ 20 12 27 ]
;
;
;
4
36 36 36
9 3
Kürze vollständig:
165  77  256
1
 ... [ 2 ]
96  112  121
2
1 5
7 3
5
;
;  ; und  nach zunehmender Größe! Welche Zahl liegt auf der Zahlengerade
3 12
12 8
8
5
7
5
5
1 3
5
5
  
; " Mitte" : 
„in der Mitte“ zwischen  und
? [   
]
8
12
8
12 3 8 12
48
Ordne die Brüche
Vier Grundrechenarten mit Bruchzahlen
(Klammern zuerst! Potenz vor Punkt vor
Strich!)
1 1 1
7
   ... 
;
2 3 4
12
2

2
2
1 2
8
 4 : (1 )  ...   ;
3
3
4
25

1 2
1
5 5  8  4 3 : (  2 )  ...  1 ;
8 3 4
6
2
2. Rechnen mit Dezimalbrüchen
endliche und unendliche periodische
Dezimalbrüche (auch Umwandlung)
57
 57 : 40  1,425 ;
40
besondere Brüche:
1  0,5 ;
2
Vier Grundrechenarten (auch) mit
Dezimalbrüchen
Umgang mit gerundeten Dezimalbrüchen, geltende Ziffern
1  0,25 ;
4
3
 3 :11  0,272727 ...  0, 27 ;
11
3  0,75 ;
4
2
1  0,125 ;
8
3  0,375 ;
8
0,6 
6
3
 ;
10 5
5  0,625 ;
8
0,4 : 0,00625  8  ...  0 ;
2,25  3,2  7,2 : 0,04  ...   172 ,8 ;
2,5493  2,5 (1 D bzw. 2 g.Z.) ;
2,5493  2,55 (2 D bzw. 3 g.Z.) ;
Welches Intervall gehört zur gerundeten Größe 3, 41 kg ? .
0, 6 
6 2
 ;
9 3
7  0,875 ;
8
3,5 2  2,5 2
72  0,125
 ...  2 ;
3
0,07535  0,075 (3 D bzw. 2 g.Z.) ;
( Antwort:  3,405 kg ; 3,415 kg  )
3. Absolute und relative Häufigkeit
Absolute Häufigkeit ist die Anzahl, wie
oft ein bestimmtes Ergebnis auftritt
Relative Häufigkeit ist der Quotient aus
der absoluten Häufigkeit und der
Gesamtzahl der durchgeführten Zufallsexperimente
Erscheint bei 75-maligem Münzwurf 42-mal Wappen, so ist 42 die absolute Häufigkeit und 42  14  0,56 die
75 25
relative Häufigkeit des Auftretens von „Wappen“ bei den 75 Würfen.
Würfle 100 mal und bestimme die absoluten und relativen Häufigkeiten für die einzelnen Wurfergebnisse!
Bestimme, nach Fächern getrennt, deine relativen Häufigkeiten für die Note „2“ im vergangenen Schuljahr! 
4. Prozentrechnung
1  100 %  33 1 %  33, 3 % ;
3
3
3
0,025  2,5 % ;
3,75  375 % ;
Darstellung beliebiger Anteile in
Prozent
3
75

 75 % ;
4 100
Berechnung von Prozentsätzen, Prozentwerten und Grundwerten:
„Prozentwert ist Prozentsatz mal
Grundwert “: P  p %  G
Diagrammdarstellungen
o
14 % von 250 € sind 14  250 €  35 € ; stelle den Anteil an einem Kreisdiagramm dar!
[ 50 , 4 ]
100
Die Verlängerung einer Strecke von 40 m Länge um 25 % führt zu einer Gesamtlänge von 1, 25  40 m  50 m .
Sachaufgaben
Das Gehalt eines Angestellten wurde zunächst um 20 % und das Folgegehalt im nächsten Jahr um weitere 10 %
auf nunmehr 2640 € aufgebessert. Wie hoch war es vor der ersten Erhöhung?
[ 2000 € ]
Entsprechen 35 % eines Grundwertes 1400 g, so beträgt dieser 1400 g : 35 %  1400 g  100  4000 g .
35
Eine Dose Kondensmilch von 10 % Fettgehalt hat 200 g Inhalt. Wie viel Gramm Wasser muss man hinzufügen,
um Milch von 4 % Fettgehalt zu bekommen?
[ 300 g ]
Wie hoch ist der gesamte Zinsertrag, wenn man 4000 € drei Jahre lang zu 5 % Zins bei der Bank anlegt und die
Zinsgutschrift a) jährlich ausbezahlt bzw. b) auf dem Konto belassen wird?
[ a) 600 € b) 630 ,50 € ]
5. Flächeninhalt von Dreiecken und Vierecken
Flächeninhalt eines Dreiecks:
A  1 a  h  1 b  h  1 c  h
a
b
c
2
2
2
(„halbe Seite  zugehörige Höhe“)
Im Dreieck ABC ist a  8,0 cm ; b  6,0 cm ; h a  6,0 cm und h c  4,8 cm .
Bestimme seinen Flächeninhalt, berechne die Längen der fehlenden Seite und Höhe und vergleiche deren Werte
Flächeninhalt von Parallelogramm
(Raute) und Trapez:
ac
A P  a  h  b  h ; AT 
h
a
b
a
2
Bestimme den Flächeninhalt einer Raute ABCD mit A ( 1,5 /  2) , B ( 4 /  3) , C (1,5 / 2) und D (4 / 3) .
mit den Maßen in einer sauberen und genauen Zeichnung des Dreieck!
2
[ 24 cm ]
Zeichne ein Parallelogramm von gleich großer Fläche, dessen eine Seite a  10 cm lang ist.
[ h  2,5 cm ]
In einem trapezförmigen Beet von A  0, 253 a Flächeninhalt sind die beiden parallelen Seiten a  7,8 m und
c  3,7 m lang. Wie groß ist ihr Abstand? Zeichne ein solches Trapez im Maßstab 1:100!
[ h  4, 4 cm ]
6. Rauminhalte
Maßeinheiten und Umrechnungen
1 m  1 000 dm  1 000 000 cm  1 000 000 000 mm ;
Rauminhalte von Würfel und Quader:
Ein Würfel hat den Rauminhalt 125 dm . Berechne seinen Oberflächeninhalt!
3
VW  a („Kantenlänge hoch 3“)
VQ  l  b  h („Länge  Breite  Höhe“)
3
3
3
3
3
3
3
3
1 l  1 dm ; 1 ml  1 cm ; 1 hl  100 l  0,1 m ;
[ 150 dm 2 ]
Ein Schwimmbecken ist 25 m lang, 12,5 m breit und 2,0 m tief. Wie viel Liter befinden sich im Becken, wenn es
bis 20 cm unterhalb des Randes gefüllt ist?
[ 562 500 l ]