Laserspektroskopie T..

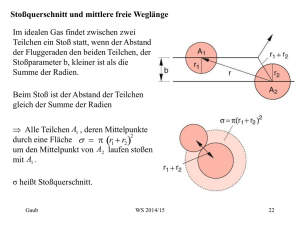
5. Dopplerfreie Zweiphotonenabsorption:
bei großen Laserintensitäten (da verbotene Übergänge
wesentlich seltener) kann das Atom zwei Photonen
absorbieren
 Drehimpulsänderung von l = 0,+2,-2 möglich
für |i> nach |f> gilt für ein bewegtes Molekül:
Ef-Ei = h(1+2)/2 + hv(k1+k2)/2
sind Photonen aus zwei antikollinearen Lichtwellen mit
 => k1 = -k2 => Dopplerverbreiterung zu 0
durch die Fluoreszenzemission vom Niveau Ef wird
Absorption nachgewiesen
1
6. Laserspektroskopie in Molekularstrahlen:
6.1 Reduktion der Doppler-Breite in
kollimierten Strahlen:
Moleküle strömen aus dem Reservoir R durch A in ein
Vakuum und die Dichte sei so gering, daß Stöße
vernachlässigbar sind => große freie Weglänge
Ziel: vx in x-Richtung verringern
Man erkennt: vx/vz  b/2d = tan 
kollimierter Molekularstrahl wird in x-Richtung vom
Laser durchkreuzt, so folgt: -kvx
 Doppler-Breite um den Faktor sin reduziert
 D*= Dsin
mit sin = vx/v b/2d
Beispiel: b = 1mm ; d = 100mm => tan  = 510-3
D*  5106Hz, wenn D  109Hz
 im Bereich der natürl. Linienbreite vieler Übergänge
Absorption wird mit LIF registriert
2
6.2 Adiabatische Abkühlung von Molekülen:
nun sei in R der Druck hoch, so daß Moleküle bei
Expansion durch A viele Stöße untereinander erfahren
adiabatisch, da Expansion zu schnell, als daß Wärme an
die Umgebung abgegeben werden kann
- in R sei Druck po, Temperatur To, Volumen Vo und
Gesamtenergie eines Mols der Masse M beträgt:
U = Utrans+ Urot+ Uvib
- Mu2/2 Strömungsenergie; Kompressionsenergie pV
 Energieerhaltung: Uo+poVo+Muo2/2 = U+pV+Mu2/2
geringes Ausströmen => uo=0; p=0
 Uo+poVo = U+Mu2/2
geht meiste Energie in Strömungsenergie über, so gilt
Mu2/2 >> U => kalter Molekularstrahl
3
durch zentrale Stöße wird Relativgeschwindigkeit v|| um
die Strömungsgeschwindigkeit u stark eingeengt und
man erhält statt der Maxwellverteilung die eingeengte
Verteilung mit charakteristischer Temperatur T|| für die
Einengung um die Strömungsgeschwindigkeit u
nicht zentrale Stöße werden durch Blenden
ausgesondert, denn vx,vy werden ausgeblendet
Beispiel:
bei Argonstrahl mit po = 1 Bar mit 3% NO2 und einem
Düsendurchmesser von 100m erhält man:
Ttrans  1K ; Trot  5-10K ; Tvib  50-100K
Zusammenfassung:
- kollimierte Molekularstrahlen reduzieren
Dopplerbreite um einige Größenordnungen
- Molekularstrahlen geringer Dichte fast stoßfrei
 Untersuchung der Wechselwirkung von Molekülen
sowie Rydbergzustände mit sehr großen
Streuquerschnitten werden möglich
- bei adiabatischer Expansion erreicht man
Temperaturen 1K
 tiefste Energieniveaus werden besetzt
 wesentliche Vereinfachung der Spektren
4
7. Optisches Kühlen durch Photonenstoß:
mit kollimierten Molekularstrahlen ließ sich thermische
Bewegung in zwei Dimensionen begrenzen (senkrecht
zum Strahl) und in Strahlrichtung einengen
optisches Kühlen erreicht „Translationstemperaturen“
T  nK
Atom A befinde sich die Zeit T im Laserfeld, welches
mit der Frequenz  auf den Übergang Ei nach Ek
abgestimmt sei und A sei echtes Zwei-Niveau-System
=> ständiges Absorbieren / Reemittieren möglich
bei hohen Intensitäten kann AbsorptionsEmissionszyklus q den Sättigungswert q=T/2
erreichen, mit  Lebensdauer vom Zustand |k>
spontane Emission statistisch in alle Raumrichtungen
 Rückstoßimpuls vernachlässigbar
Rückstoßimpuls der Laserphotonen addiert sich zu:
p = qhk/2 => ERückstoß = qh22/82Mc2
mit M = Masse des Atoms
5
vi sei Anfangsgeschwindigkeit der Atome, so ändert
sich die Geschwindigkeit pro Absorptionszyklus:
v = h/2Mc => Abbremsen
Problem:
Doppler-Verschiebung ändert sich mit der
Geschwindigkeit
 = o+kv => (t) = o+kv(t)n
 entweder Laserfrequenz  muß sich synchron mit
v(t) ändern oder Absorptionfrequenzen o ändert
sich
- durch den Zeeman-Verschiebung läßt sich o
anpassen
- Laserfrequenz läßt sich durch Amplitudenmodulation
(Erzeugung von Seitenbändern) anpassen
mit einem schwachen Laser läßt sich wieder LIF
betreiben
Erweiterung: bei guter Strahlkollimation lassen sich
Atome ablenken und somit die Absorption einzelner
Photonen nachweisen
Problem:
- ohne zusätzliche Erweiterungen ist dieses Verfahren
auf echte Zwei-Niveaus beschränkt
- nicht für Moleküle geeignet, da diese nach Anregung
in andere Schwingungs-Rotations-Niveaus übergehen,
somit für folgenden Pumpvorgang verloren gehen
6
8. Speicherung langsamer Teilchen im
Lichtfeld:
Beispiel: Rückstoßkraft im 3 dimensionalen Lichtfeld
hier müssen die Atome stark vorgekühlt (einige mK)
werden, um sie im Lichtfeld speichern zu können, da
Stabilisierungsenergie Epot sehr gering
 kT < Epot
Laserfrequenz  < o , so wirkt auf das Atom mit der
Geschwindigkeit v immer eine rücktreibende Nettokraft
7
Grund:
- läuft die Laserwelle dem Atom entgegen
 durch Doppler-Effekt zur Resonanz hin verschoben
- läuft die Laserwelle in gleicher Richtung wie das
Atom
 durch Doppler-Effekt von der Resonanz weg
verschoben
rücktreibende Kraft hemmt die Bewegung des Atoms
und v  0
 „optical molasses“
untere Grenze der Kühlung folgt aus der natürlichen
Linienbreite : kTmin = h/4
Beispiel:
Ca-Atome mit  = 20kHz => Tmin = 240nK
8
9. Ionenfallen:
zwei verschiedene Anordnungen:
magn. Penning-Falle und elektr. HF-Quadrupolfalle
zwischen den hyperbolischen Kappen und der
Ringelektrode liegt eine Wechselspannung
U = Uo+Vo cosot
Potential:  = U(r2-2z2)/2ro2
 Bewegungsgl.: mr = F = -grad 
mit Masse m und Ladung q des Teilchen
man erhält folgende Matthieu‘schen
Differenzialgleichungen:
d2x/dt2 + o2(a-2bcosot)/4 mit den Parametern
a = 4qUo/mro2o2
und b = 2qVo/mro2o2
 nur für bestimmten Wertebereich der Parameter a
und b gibt es stabile Lösungen
9
Ionen beschreiben harmonische Schwingung in der x-yEbene mit r und in der z-Richtung mit z = 2r
gespeicherte Ionen können wieder mit LIF analysiert
werden
10