Elektrotechnik I MAVT
Werbung

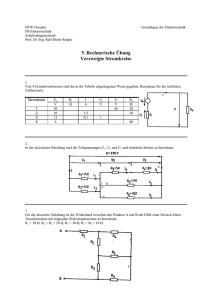
Prof. Dr. Q. Huang Elektrotechnik I MAVT Prüfung H07 BSc 23.08.2007 Elektrotechnik I MAVT Prüfung H07 BSc 23.08.2007 1. [30P] DC-Aufgaben (a) [9P] Betrachten Sie die Schaltung in Abbildung 1 und lösen Sie die nachfolgenden Aufgaben. Vereinfachen Sie die Resultate so weit wie möglich (keine Doppelbrüche, -Zeichen auflösen). I2 R1 R2 Ix I R3 R4 V 4 R5 Abbildung 1: Schaltung zu Aufgabe 1a. i. [3P] Berechnen Sie die Spannung V4 . ii. [3P] Wie gross ist der Strom I2 ? iii. [3P] Wie gross ist der Strom Ix ? (b) [4P] Berechnen Sie die Thévenin-äquivalente Ersatzschaltung für die Schaltung in Abbildung 2, indem sie die nachfolgenden Fragen beantworten. Vereinfachen Sie die Resultate so weit wie möglich (keine Doppelbrüche, -Zeichen auflösen). a R2 E I R1 b Abbildung 2: Schaltung zu Aufgabe 1b. i. [2P] Wie gross ist der äquivalente Widerstand RTh ? ii. [2P] Was ist der Wert der äquivalenten Spannungsquelle ETh ? Seite 1 von 6 Elektrotechnik I MAVT Prüfung H07 BSc 23.08.2007 (c) [7P] Berechnen Sie die Norton-äquivalente Ersatzschaltung für die Schaltung in Abbildung 3, indem sie die nachfolgenden Fragen beantworten. Vereinfachen Sie die Resultate so weit wie möglich (keine Doppelbrüche, -Zeichen auflösen). a I R2 R1 E R3 b Abbildung 3: Schaltung zu Aufgabe 1c. i. [3P] Wie gross ist der äquivalente Widerstand RN ? ii. [4P] Was ist der Wert der äquivalenten Stromquelle IN ? (d) [10P] Analysieren Sie die Schaltung in Abbildung 4 mit dem Maschenstromverfahren. R2 R3 E1 Vx I M1 M2 E2 R4 R1 Abbildung 4: Schaltung zu Aufgabe 1d. i. [2P] Welcher Strom M1 fliesst in der ersten Masche? ii. [3P] Schreiben Sie eine Gleichung für die Spannung entlang der zweiten Masche mit Hilfe des KVL (Kirchhoff’s Voltage Law) auf. iii. [2P] Wie gross ist der Maschenstrom M2 in der zweiten Masche? iv. [3P] Wie gross ist die Spannung Vx ? Seite 2 von 6 Elektrotechnik I MAVT Prüfung H07 BSc 23.08.2007 2. [30P] AC-Aufgaben (a) [9P] RCL-Vereinfachung Betrachten Sie die Schaltung in Abbildung 5 und lösen Sie dazu die folgenden Aufgaben. 3R a 2C 6L 3C 2R 2L C Ea 3R 2L L b 2C 2R R 3L 3C R Eb Abbildung 5: Schaltung zu Aufgabe 2a. i. [6P] Vereinfachen Sie die Schaltung zwischen den Klemmen a und b, d. h. ohne die Spannungsquellen zu beachten. ii. [2P] Welcher Strom fliesst durch die Schaltung, falls die Spannungsquellen berücksichtigt werden? iii. [1P] Die Schaltung zwischen den zwei Klemmen stelle einen Schwingkreis dar. Handelt es sich um einen Serien- oder Parallelschwingkreis? (b) [8P] Kondensator und Spule i. [2P] Ein Plattenkondensator bestehe aus zwei Platten mit je einer Fläche von 100 mm2 und einem Dielektrikum mit einer Dicke von 0.4 mm dazwischen. Die Kapazität des Kondensators betrage 16.6 pF. Wie gross ist die relative Permittivität des Dielektrikums (die Permittivität im Vakuum ist F 0 = 8.85 · 10−12 m )? ii. [3P] Mit welchen Mitteln kann die Kapazität eines Plattenkondensators erhöht werden (3 aufzählen)? iii. [3P] Welche Ladung befindet sich auf den Platten, falls die gespeicherte Energie 48.21 pJ beträgt? Seite 3 von 6 Elektrotechnik I MAVT Prüfung H07 BSc 23.08.2007 (c) [13P] Transientes Verhalten Betrachten Sie die Schaltung in Abbildung 6. Die Schalter φ1 seien seit unendlich langer Zeit geschlossen und werden zum Zeitpunkt t = 0 geöffnet. φ2 ist nur im Interval 0 < t ≤ t1 geschlossen, und φ3 sind im Interval t1 < t ≤ ∞ geschlossen. Beantworten Sie die nachfolgenden Fragen. φ2 φ3 φ1 I C φ3 φ1 R Abbildung 6: Schaltung zu Aufgabe 2c. i. [3P] Drücken Sie die Spannung VC (t), die über dem Kondensator C abfällt, und die Energie EC (t), die im elektrischen Feld des Kondensators C gespeichert ist, für den Zeitraum 0 < t ≤ t1 als Funktion der Zeit aus. ii. [2P] Wie gross ist die Spannung VC nach unendlich langer Zeit für t > t1 ? Was ist mit der gespeicherten Energie passiert? iii. [4P] Geben Sie eine Formel für den Strom IC (t) und die Spannung VC (t) für den Zeitbereich t ≥ t1 an. iv. [4P] Geben Sie die Instantanleistung PR (t) im Widerstand R für t > t1 als Funktion der Zeit an, und berechnen Sie das Integral der Instantanleistung im Interval t1 ≤ t ≤ ∞. Was stellt das Integral dar? Seite 4 von 6 Elektrotechnik I MAVT Prüfung H07 BSc 23.08.2007 3. [30P] Vermischte Aufgaben (a) [18P] Betrachten Sie die Verstärkerschaltung in Abbildung 7 und beantworten Sie dazu folgende Fragen: φ1 R1 E C A vo Abbildung 7: Schaltung zu Aufgabe 3a. Ignorieren Sie zunächst den Schalter, d. h. betrachten Sie ihn als nicht leitend (offen). i. [2P] Berechnen Sie die Übertragungsfunktion H (jω) = vo . E ii. [1P] Was ist die Funktion der Schaltung (in Worten)? Schliessen Sie nun den Schalter wieder in Ihre Betrachtungen mit ein. Er sei geschlossen (leitend) bis zum Zeitpunkt t = 0, danach geöffnet (nicht leitend). iii. [3P] Berechnen Sie vo (t) im Zeitbereich. iv. [3P] Sie haben nun weitere Schaltungselemente wie Widerstände, Spulen, Kondensatoren und OpAmps zur freien Verfügung. Ergänzen Sie die Schaltung am Ausgang so, dass das Vorzeichen der Übertragungsfunktion H invertiert wird (Zeichnung). v. [2P] Wie wird der Phasengang durch das Ausführen der vorherigen Teilaufgabe beeinflusst? vi. [2P] Wo befindet sich die Polstelle der Übertragungsfunktion? vii. [4P] Die Polstelle soll nun zu höheren Frequenzen (im Bodeplot) geschoben werden. Wie muss die Schaltung dazu (durch Hinzufügen eines Schaltungselements) modifiziert werden? Berechnen Sie die neue Übertragungsfunktion Hpshift (jω). Vernachlässigen Sie dazu den Einfluss von Teilaufgabe iv. viii. [1P] Was ist die Funktion der neuen Schaltung? Seite 5 von 6 Elektrotechnik I MAVT Prüfung H07 BSc 23.08.2007 (b) [12P] In Abbildung 9 ist ein komplexer Widerstand mit einer Spannungsquelle zu sehen. Die Spannungsquelle liefert eine sinusförmige Spannung u (t) = û sin (ωt + φ0 ), die Frequenz beträgt f = 2 kHz. iZ(t) u(t) Z uZ(t) Abbildung 9: Schaltung zu Aufgabe 2b. Über dem komplexen Widerstand Z wird eine Spannung UZ = 36 V (−20◦ ) und ein Strom IZ = 120 mA (40◦ ) gemessen. i. [3P] Wie gross sind der Phasenwinkel φ0 , der Scheitelwert û der Spannungsquelle und der Leistungsfaktor cos (φ)? ii. [2P] Berechnen Sie den Wert des komplexen Widerstandes Z. Der komplexe Widerstand Z besteht aus einem reellen Widerstand R und einem reaktiven Element (Spule oder Kondensator). iii. [1P] Ist das reaktive Element eine Spule oder ein Kondensator? iv. [1P] Wie gross ist R? v. [3P] Wie gross ist der Wert der Spule L bzw. des Kondensators C? vi. [2P] Wie gross ist die verbrauchte Wirkleistung? Seite 6 von 6