Ubungsaufgaben Technische und Wirtschaftwissenschaftliche Universität Budapest

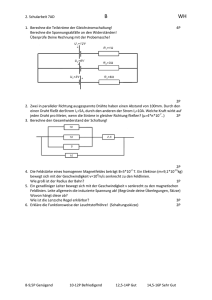
Technische und Wirtschaftwissenschaftliche Universität Budapest
Lehrstuhl für Strömungslehre
2003
Dr. Miklós Blahó
Strömungslehre
Übungsaufgaben
1
Hydrostatik.............................................................................. 3
2
Kinematik................................................................................ 8
3
Bernoullische Gleichung....................................................... 10
4
Impulssatz ............................................................................. 15
5
Hydraulik .............................................................................. 20
6
Gasdynamik .......................................................................... 24
Lösungen..................................................................................... 27
1
Hydrostatik............................................................................ 27
2
Kinematik.............................................................................. 30
3
Bernoullische Gleichung....................................................... 32
4
Impulssatz ............................................................................. 35
5
Hydraulik .............................................................................. 38
6
Gasdynamik .......................................................................... 41
1
Hydrostatik
Allgemeine Konstanten für jede Aufgabe: R
1/1
pA
p0
? Pa
1/2
p1
p2
? Pa
1/3
Strecke 1-2:
12
1.3 kg / m3
Strecke 3-4:
34
1.1 kg / m3
1/4
p4
p1
? Pa
p0
105 Pa (für die Kalkulation von
Umgebung (Luft):
Im Schornstein (Rauchgas):
p1
p2
? Pa
)
T1 0 C
p2 760 mmHg
T2
250 C
287 J / kg K , g
9.81 N / kg
Hydrostatik
1/5
4
Der Überdruck in einer Gasleitung (siehe Abbildung) am
Erdgeschoss beträgt 500 Pa. Man berechne den Überdruck in der
Höhe von 20m! In der Gasleitung findet kein Materialtransport
statt.
Luft
1.2 kg / m 3
Gas
0.7 kg / m 3
1/6
z
p0 105 N / m 2
0
1.2 kg / m
0
a.) T0
1/7
0
288 J / kgK
? Pa , wenn die Temperatur im Bereich
z
2000m konstant ist.
p0 105 N / m 2
1.25 kg / m3
0
zA
R
0.5 105 N / m 2
pA
z
Luft
? K
b.) p A
0
3
Luft
R
288 J / kgK
? m wenn die Temperatur im Bereich 0
ist.
1/8
Der Behälter ist mit Öl gefüllt.
Öl
950 kg / m 3
a 3 m / s2
pA
p0
? Pa
z
z A konstant
Hydrostatik
1/9
5
Der Behälter ist mit Öl gefüllt.
Öl
pA
950 kg / m 3
p0
0 Pa
a ? m / s2
1/10
Der Kesselwagen bewegt sich in einer Kurve
mit der zentripetaler Beschleuningung von
3 m / s2 .
a
Der Tank ist mit Wasser gefüllt.
Wie groß ist die Erhöhung der
Wasseroberfläche an der A-B Seite?
Wie groß ist die an die A-B Wand
angreifende
Kraft,
wenn
der
Tankwagen 1.6m lang ist?
a.)
b.)
1/11
Man berechne den Gleichgewichtszustand
der Flüssigkeitsoberflächen, wenn sich das
U-Rohr mit einer Beschleunigung von
g
bewegt!
2
a
1/12
n 1000 1 / min
Wasser
pA
p0
1000 kg / m 3
? Pa
Hydrostatik
1/13
6
Das Rohr ist mit Wasser gefüllt. Der
Umgebungsdruck ist p0 105 Pa .
Bei welcher Winkelgeschwindigkeit wird
pA
1/14
0.8 105 Pa sein?
Die Auswirkung der Gravitation ist vernachlässigbar.
800 kg / m3
n
6000 1 / min
pA
1/15
p0
Die Auswirkung der Gravitation ist vernachlässigbar.
100 1 / s
Wasser
Öl
pA
1/16
?
1000 kg / m 3
800 kg / m 3
p0
? Pa
Wie groß ist die Oberfläche deren Eisscholle, die ein Mensch mit dem Gewicht von 75kg
tragen kann, wenn die Dicke der Eisscholle 10cm und die Dichte des Eises 900 kg/m3 ist?
Hydrostatik
1/17
7
Das Seil ist gewichtlos.
Würfel
2300 kg / m 3
Wasser
1000 kg / m 3
rKugel
300 mm
GKugel
200 N
a ? m/s2
1/18
Man berechne die Antriebskraft von einem mit heißen
Luft (60°C) gefüllten Ballon, wo der Durchmesser des Ballons 10m, die
Umgebungstemperatur 0 C ist! Der Druck im Ballon und draußen beträgt 105 Pa. Das
Gewicht des Ballons kann vernachlässigt werden.
1/19
p1
p2
20 N / m 2
800 kg / m 3
Flüssigkeit
wenn der Ablesefehler der Flüssigkeitssäule
?
von
1mm einen Relativfehler von
verursacht.
1/20
Nach der Auffüllung des U-Rohrs
werden beide Kugelhähne geschlossen.
Während der Rotation sinkt die
Wasseroberfläche in dem linken Rohr
bis Punkt B (s Abb.).
p0
105 Pa
p Sättigungsdruck
T
konst
? 1/ s
2 10 4 Pa
2% in p1
p2
2
2/1
Kinematik
Die Druckerhöhung ist vernachlässigbar klein.
40 m3 / s
qv
t1 15 C
2/2
t2
80 C
v1
? m/s
v2
? m/s
Zweidimensionale Strömung:
v
10 r
rot v
2/3
z A
Rotationsymmetrische Strömung.
vdurchschn.
vmax
2/4
? 1/ s
?
Zweidimensionale instationäre Strömung.
vy
0
vx
5 yt 2
Man
berechne
die
lokale
Beschleunigung im Punkt 'A' bei t
und
0.5 s !
konvektive
Kinematik
2/5
9
Man berechne die Zirkulation entlang der punktgestrichelte
Linie!
v
2
r2
? m2 / s
2/6
Man berechne die konvektive Beschleunigung!
v1 20 m / s
const.
akonv
A
? m / s2
3
3/1
Bernoullische Gleichung
pt
3 105 Pa
p0
105 Pa
v
3/2
? m/s
v 10 m / s
u
4 m/s
103 kg / m3
p A p0 ? Pa
3/3
Die Reibungsverluste sind vernachlässigbar.
1.2 kg / m3
v2
3/4
? m/s
Stationäre Strömung.
qV
0.1 m3 / min .
h ? m
Bernoullische Gleichung
3/5
3/6
3/7
p1 1.6 105 Pa
p2
1.2 105 Pa
qV
? m3 / s
a 12 m s
2
p0
105 Pa
pt
0.5 105 Pa
qV
? m3 / s
25 1 / s
w ? m/ s
(w: Relativgeschwindigkeit)
3/8
w 3 m/ s
? 1/ s
(w: Relativgeschwindigkeit)
11
Bernoullische Gleichung
3/9
3/10
p0
105 N / m 2
pA
0
vA
4 m/s
aA
? m / s2
p0
105 Pa
p1
0.9 105 Pa
Die Reibungsverluste sind
vernachlässigbar.
berechne
die
a.) Man
Anfangsbeschleunigung 'a' beim Öffnen des Hahnes!
b.) H
? m im stationären Fall?
3/11
Man
berechne
die
Anfangsbeschleunigung 'a' im
Punkt 'B' beim Öffnen des Hahnes!
3/12
Man berechne die Anfangsbeschleunigung
'a' beim Austritt!
pt
2 104 N / m 2 (Überdruck )
v2
0 m/ s
12
Bernoullische Gleichung
3/13
13
v 1m/ s
a 1 m / s2
Die
Reibungsverluste
sind
vernachlässigbar. Man berechne
die
Schubkraft,
die
die
Kolbenstange bewegt!
3/14
u
72 km / h
v
4 m/s
Die Reibungsverluste sind vernachlässigbar.
a.) qV
? m3 / s
b.) Man berechne die Leistung der Schubkraft, die
das Rohr in Bewegung hält!
3/15
alk
800 kg / m3
Luft
1.2 kg / m3
v
3/16
? m/s
Der Innendurchmesser einer Messblende ist d
Kompressibilitätsfaktor
1.3 kg / m3 .
qV
? m3 / s
1.
Das
gemessene
200 mm . Kontraktionsziffer
Druckabfall
ist
p
0 .7
600 N / m 2 .
Bernoullische Gleichung
3/17
14
Die Breite der Strömung ist 1m.
a.) Man bestimme die vertikale Geschwindigkeitsverteilung am Ausfluss! (Diagram)
b.) Man bestimme der Volemenstrom qV m3 / s !
3/18
Horizontale, zweidimensionale Potentialströmung.
r1
0.5 m
r2
0.8 m
v0
5 m/s
a.) Man bestimme die Geschwindigkeitsverteilung in dem Bogen!
b.) p A
pB
pA
pB
c.)
2
v0
2
? Pa
f
Diagramm!)
r2
? (Man zeichne ein
r1
4
4/1
Impulssatz
Man bestimme die auf dem kegelförmigen
Rohrstück wirkende, horizontale Kraft!
qV
3.5 m3 / min
Die Reibungsverluste sind vernachlässigbar.
4/2
v1
30 m / s
u 13 m / s
Die Reibungsverluste sind vernachlässigbar.
a)
v2
? m/s
b) Man bestimme den Ablenkungswinkel
(Winkel zwischen v1 und v 2 )!
c) Man berechne die auf die Schaufel wirkende Kraft!
d) Wie verändert sich die kinetische Energie von 1kg Wasser während der Ablenkung?
4/3
v 10 m / s
Die Reibungsverluste und die Auswirkung der
Gravitation sind vernachlässigbar.
Man berechne die auf die Krümmung wirkende
Kraft!
4/4
v 10 m / s
u
2 m/ s
Die Reibungsverluste und die Auswirkung der
Gravitation sind vernachlässigbar.
Man berechne die auf den bewegenden,
kegelförmigen Körper wirkende Kraft!
Impulssatz
4/5
16
v 10 m / s
Hg
13600 kg / m 3
Die Reibungsverluste und die Auswirkung der
Gravitation sind vernachlässigbar.
Man berechne die auf den kegelförmigen Körper
wirkende Kraft!
4/6
A 10 4 m 2
v 10 m / s
Die Reibungsverluste und die Auswirkung der Gravitation
sind vernachlässigbar.
Man berechne das Gewicht des Kegels (’G’ [N])!
4/7
Die Reibungsverluste sind vernachlässigbar.
G 1N
v0
4/8
? m/ s
Zweidimensionale Strömung.
v 30 m / s
a) F
? N
b) A1 A2
?
Impulssatz
4/9
17
Zweidimensionale Strömung.
Die Reibungsverluste und die Auswirkung
der Gravitation sind vernachlässigbar.
?
4/10
Zweidimensionale Strömung.Die Reibungsverluste und die
Auswirkung der Gravitation sind vernachlässigbar.
v 10 m / s
15
G ? N
4/11
Die Reibungsverluste sind vernachlässigbar.
Der Zylinder wird mit der Hilfe des
Wasserstrahles in seiner Position (s. Abb.)
gehalten.
G 10 N
h ? m
4/12
v 10 m / s
u
6 m/s
Die Reibungsverluste sind vernachlässigbar.
Man berechne die durch den Wasserstrahl auf das
Schaufelrad übertragene Kraft!
Impulssatz
4/13
18
v
20 m / s
u
6 m/s
Die Reibungsverluste sind vernachlässigbar.
Man berechne die x und y Komponenten der auf das
Schaufelrad wirkenden Kraft!
4/14
v1
1
2 m/s
1.2 kg / m 3
t1
20 C
t 1'
t2
300 C
Die Reibungsverluste, die Auswirkung der Gravitation und die
aus der Druckveränderung stammende Dichteveränderung sind
vernachlässigbar.
4/15
p1
p2
v1
2 m/s
0
? Pa
1.29 kg / m3
t0
0C
t2
273 C
Die Reibungsverluste und die aus der Druckveränderung
stammende Dichteveränderung sind vernachlässigbar.
4/16
qV
? m3 / s
v1
20 m / s
h
1 kg / m3
? m
Impulssatz
19
4/17
Die Reibungsverluste im Rohr sind vernachlässigbar.
p1 p0 ? Pa
4/18
Die Volumenströme durch die Röhrchen sollen
gleich sein. Der Verlust infolge der
Durchmesseränderung
muss
in
Betracht
genommen werden.
h ? m
4/19
Stationäre Strömung.
h ? m
4/20
Man bestimme die wegen des Entfernens der
Zwischenplatte auftretende Volumenstromzunahme!
qV
ohne Zwischenplatte
qV
mit Zwischenplatte
?
5
5/1
5/2
Hydraulik
Die Breite des Spaltes ist 100 mm (senkrecht auf die
Zeichnungsebene).
v
0.5 m / s
F
0.1 kg / ms
? N
Die Reibungsverluste im Konfusor sind
vernachlässigbar.
v1
0.5 m / s
850 kg / m3
10 5 m 2 / s
p1
5/3
p0
? Pa
Die Reibungsverluste im Zwischenstück
sind vernachlässigbar.
v1 10 m / s
1.2 kg / m3
14 10 6 m 2 / s
p1
p0
? Pa
5/4
Man bestimme den Zusammenhang zwischen dem Durchmesser und der Reynoldssche Zahl
sowie zwischen dem Durchmesser und dem Rohrreibungsverlust in einem glatten Rohr im
laminären und turbulenten Fall, wenn der Volumenstrom konstant ist!
5/5
Man bestimme den Zusammenhang zwischen dem
Rohrreibungsverlust im laminären und turbulenten Fall!
5/6
Man bestimme den Durchmesser dessen Rohres, durch das Öl mit dem Volumenstrom von
qV 2 10 4 m3 / s fließt ( Öl 800 kg / m3 , Öl 10 4 m 2 / s ). Das Rohr ist 10m lang, und
Volumenstrom
der maximale zur Verfügung stehende Druckabfall ist 2 10 5 Pa .
und
dem
Hydraulik
5/7
qV
21
8000 m3 / h
1.2 kg / m3
0.025
D
5/8
0.8
p1
p0
qV
1200 l / min
13.6 103 kg / m3
Hg
h
5/9
? Pa
? m
Die Schmiervorrichtung muss Öl mit dem Volumenstrom
0.05 10 3 m 3 / s fördern. Bei der Kalkulation der
von q V
Reibungsverluste kann das Rohr als gerade betrachtet
werden.
800 kg / m3
Öl
Öl
d
5/10
10 4 m 2 / s
? mm
Die Reibungsverluste der Bögen sind vernachlässigbar.
Wasser
qV
1.3 10 6 m 2 / s
? m3 / s
Hydraulik
5/11
Wasser
qV
5/12
22
? m3 / s
Hidraulisch glatte Rohrinnenwand.
Wasser
5/13
1.3 10 6 m 2 / s
qV
5l/s
p1
p0
? Pa
Hidraulisch glatte Rohrinnenwand.
Wasser
5/14
1.3 10 6 m 2 / s
1.3 10 6 m 2 / s
qV
180 l / min
p1
p0
? Pa
Hidraulisch glatte Rohrinnenwand, stationäre Strömung.
Wasser
1.3 10 6 m 2 / s
v1 1 m / s
a) H
? m
b) p1
p0
? Pa
Hydraulik
5/15
23
Ein Zapfen dreht sich in einer Bohrung mit der Drehzahl von 2880 1/min. Die
geometrischen Daten sind: Zapfenlänge 100mm, Zapfendurchmesser 60mm, Spaltenbreite
zwischen Zapfen und Bohrung 0,2mm, Viskosität des Öles
Öl
0.01 kg / ms . Man
berechne die benötigte Drehleistung. Wie kann diese Leistung reduziert werden?
5/16
a) Man
berechne
Auslassdurchmesser
den
des
Konfusors
d 2 , wenn die
Höhe des
12m ist!
Wasserstrahles
b) Man
berechne
Volumenstrom
den
q V m3 / s
durch das Rohr! Die
Reibungsverluste der Bögen,
des
Konfusors
sowie
zwischen Luft und Wasser
sind vernachlässigbar.
5/17
Mit der Hilfe der Rohrleitung (s. Abb.) wird Wasser mit dem Volumenstrom von
qV 18 m3 / h gefördert.
a) Man berechne den minimalen Durchmesser des Rohres!
b) Man gebe die maximale Dammhöhe an, über dem der Transport noch möglich ist!
(Prinzipielle Atwort)
6
6/1
Gasdynamik
p1 1.5 bar , p2
1 bar
T1
300 K
cp
1000 J / kg K
1 .4
Izentropische Zustandsänderung.
v2
6/2
? m/s
p1 1.3 105 Pa, p2
T1
273 K
R
287 J / kg K
1.4
105 Pa
Izentropische Zustandsänderung.
qm
6/3
? kg / s
p1 1.4 bar , p2
t1
1 bar
20 C
1 .4
Izentropische Zustandsänderung.
a)
t2 stat
? C
b)
t2 total
? C
(Die Temperatur wird mit Hilfe eines Staupunktthermometers gemessen)
6/4
p1
4 bar , p2
T1
300 K
R
287 J / kg K
1.4
1 bar
Izentropische Zustandsänderung.
qm
? kg / s
Gasdynamik
6/5
p1
25
4 bar , p2
t1
70 C
R
287 J / kg K
1.4
1 bar
Izentropische Zustandsänderung.
d min
6/6
? mm
Man gebe die Formel an, mit dem v 2 bestimmbar ist!
a)
p2
p1
0.99
b)
p2
p1
0.6
c)
p2
p1
0.4
Izentropische Zustandsänderung.
6/7
Lufttemperatur
R
t
40 C ,
Strömungsgeschwindigkeit
v 180 m / s ,
1 .4 ,
287 J / kg K .
Man berechne die Machsche Zahl (Ma)!
6/8
Die Temperatur von Karbon-dioxide t
20 C , Machsche Zahl Ma
0 .3 .
1 .3 ,
R 189 J / kg K .
Man bestimme Strömungsgeschwindigkeit! v m / s
6/9
Eine Rakete fliegt in der Atmosphäre ( tUmgebung
u
400 m / s .
cp
1000 J / kg K
tA
? C
23 C ) mit der Geschwindigkeit
Gasdynamik
6/10
Ein Flugzeug fliegt in der Atmosphäre tUmgebung
u
R
0 C mit der Geschwindigkeit von
200 m / s . Die relative Geschwindigkeit w 2 ist 250 m / s in einem bestimmten Punkt
des Flügels. R
6/11
26
287 J / kg K ,
287 J / kg K , c p
1.4 . Man berechne die Machsche Zahl in dem Punkt!
1000 J / kg K ,
1 .4 .
a) Man berechne den zu izentropischen
Aussfluss benötigten Durchmesser d 2 !
b) Man bestimme die Schubkraft des
Raketentriebwerkes F N !
Lösungen
1
Hydrostatik
1/1
pA
p0
6200 N / m 2
1/2
p1
p2
12360 N / m 2
1/3
p4
p1
392 N / m 2
1/4
p1
p2
486 N / m 2
1/5
Der Überdruck beträgt am
oberen Ventil 600 Pa.
1/6
a.)
T0
b.)
dp
dz
pA
p0
ln
p0
0R
h
p
p0
g
dp
p
pA
p0
pA
1/7
290 K
5650 m
0g
p0
0g
p0
0g
zA
zA
0.788 105 N / m 2
Lösungen
28
7.23 103 N / m 2
1/8
pA
1/9
a
1/10
a)
h
0.422 m
b)
F
1400 N
p0
2.45 m / s 2
1/11
Die Oberfläche im linken Rohr befindet sich genau in der Krümmung des Rohres, die Höhe
der Wassersäule im rechten Rohr ist 100 mm.
1/12
Das Volumen im Stillstand und bei Rotation ist gleich.
1 2
r z1
2
Für die Punkte mit gleichem Potenzial:
R 2 z0
r2 2
2 gz1
0 ; r2
2
2
Aus den zwei Gleichungen folgt:
g z1
1 2 gz1
z1 z1
2 2
R 2 z0
pA
1/13
p0
z0
g
R
R2
2
g zA
2
0.236 m
14300 N / m 2
Man wende die Gleichung:
p
gz
r2
2
2
const .
für die Punkte mit bekanntem Druck an! (Punkt A und ein Punkt der freien Oberfläche im
rechten Rohr) Für die Winkelgeschwindigkeit erhält man
1/14
Man wende die Gleichung p
gz
an!
const.
r0 2
2
p0
2
pA
p0
2
rA2
2
r02
19.7 105 N / m 2
r2
2
21.4 1 / s .
2
const für die Oberfläche der Flüssigkeit
Lösungen
1/15
29
Man wende die Glechung p
gz
r2
2
2
const erstens für die Ölsäule und danach
für die Wassersäule an! Mit der Substraktion der Gleichungen erhält man den folgenden
Ausdruck:
2
pA
p0
2
1/16
A 7.5 m 2
1/17
a
0.3 m
1/18
F
1200 N
1/19
h
20
800 9.81
l
sin
1/20
1mm
0.02
Öl
0.12
0.052
2.55 mm
50 mm
2.55
50
81.8 1 / s
0.051
2.9
Wasser
0.152
0.12
9.25 104 Pa
Lösungen
30
2
Kinematik
2/1
v1 10 m / s ; v2
2/2
Lösung im karteschischen Koordinatensystem:
vx
c
vx
10 r
4
vy
y
x
v
; v y v cos
r
r
y
y
10
10
2
4
r
x
y2
v
sin
y
r
10 r
vy
6 .9 m / s
x
r
x
r
10
x2
10
y2
4
vy
x2
y2
rot v
vy
z A
y2
1 2
x
y2
4
2
x
y2
3
1 2
x
y2
4
x2 y2
3
vx
y
x
x
4
2x
im Punkt A : x, y
x
10
x
4
x
10
x
x
2
4
2x
vx
y
im Punkt A
50 100 0.1
vy
(0.1, 0)
x
50 0.1
100 0.1
47.5 1 / s
Lösung mit Polarkoordinaten:
rot c
dc
dr
z A
c
r
10
A
1
2 r
10
r
15
r
15
0 .1
47.5 1 / s
2/3
v
r
r0
vmax 1
7
Man teile den Querschnitt in elementaren Ringen mit der Breite 'dr' auf und integriere die
elementare Volumenströme für den ganzen Querschnitt!
vDurchschn.
1
r02
1 r
2 vmax
2 r0
r0
1
2r v(r ) dr
0
2
1 r
2 vmax
9 r0
r
r
2 v
r0 r0
0
9 1
vmax 1
0
r
d
r0
2
9
1
r
vmax 1
2
r
0
0
7
vmax
9
r
r0
vdurchschn.
vmax
7
d
7
9
r
r0
0.778
Lösungen
31
Für eine beliebige Potenz:
v
2/4
vmax 1
alokale
2
v1r12
v
x
n
n 2
2.61 m 2 / s
r2 v
r1 v1
v
vdurchschn.
vmax
0
v ds
2/5
n
5 m / s2
y 1
t 0.5
akonvektive
2/6
r
r0
1
r2
v r
r x
akonvektive
akonvektive
v1r12
v
A
v
x
r
x
2
r3
2v12 r14 r
x
r5
2
4
2 20 0.05 0.05
5
0.075
0.8
132 m / s 2
Lösungen
32
3
3/1
Bernoullische Gleichung
v2
2
pt
p0
g h
v 19.8 m / s
3/2
pA
3/3
Wasser
qV
A
2 g
3/4
h
3/5
qV
3/6
pt
qv
3/7
p0
2
v u
g h
2
2
v2
1.8 104 Pa
100
50
4
1
v
7.4 m / s
0.141 m
0.793 m3 / s
g a h
p0
v2
2
0.00589 m3 / s
In einem absoluten Koordinatensystem ist die Strömung rotationsfrei ( rot v
0 ). Für die
Rotation des Geschwindigkeitsfeldes in einem mitrotierenden Koordinatensystem kann man
schreiben: rot w
2w
2 . Das kann man in den Term
w rot w d s einsetzen, so erhält man
d s für die Coriolis Kraft. ( w – Relativgeschwindigkeit) Mit den Umformungen
kann man die Bernoullischen Gleichung in folgenden Form schreiben:
r1 2 r12 2 v22
r2 2
g h 2
2
2
2
2
Sei Punkt 1 auf der Wasseroberfläche auf dem Radius r1, Punkt 2 am Ausflussquerschnitt
auf der oberen Ende des Rohres.
v2
10.8 m / s
Lösungen
24 1 / s
3/8
3/9
33
A
0
v
ds
t
g h
0
aA l
a.) a t
0
b.) H
1.52 m
B
3/11
A
v
ds
t
a A 3m
24.1 m / s 2
aA
3/10
A
v A2
2
p0
v
ds
t
6.55 m / s
aB 10
5
5
20
7 .5 a B
aB
t 0
1.31 m / s 2
3/12
a2
t 0
7.94 m / s 2
3/13
F
3/14
a)
Man schreibe die Bernoullische-Gleichung in einem zum Rohr befestigten, relativen
Koordinatensystem zwischen einem Punkt der Oberfläche (Punkt 1) und einem Punkt des
Ausflussquerschnittes (Punkt 2). In diesem System wird die Relativgeschwindigkeit
451 N
w1
24 m / s . Aus der Bernoullische-Gleichung:
w2
23.4 m / s
qV
0.116 m3 / s
b)
Mit der Leistung der Schubkraft wird die potenzielle und die kinetische Energie der
Flüssigkeit vergrößert. Die Veränderung der kinetischen Energie muss aus den
Absolutgeschwindigkeit 'v' gerechnet werden.
v2
P
w22
w12
qV g h
w22
w12
2
8.85 kW
.
Lösungen
3/15
34
2
v
p
36 m / s
Luft
d2
4
2
p
0.67 m3 / s
3/16
qV
3/17
Infolge der geraden und paralellen Stromlinien im
Auslassquerschnitt
tritt
nur
eine
hidrostatische
Druckveränderung in vertikalen Richtung auf. Aus dieser
hidrostatischen Druckveränderung folgt eine konstante
Auslassgeschwindigkeitsverteilung.
3.15 m 3 / s .
qV
3/18
a) In der Krümmung v
b) vdurchschn.
r2 r1
vdurchschn. r2
r
ln 2
r1
K
K
r2
vA
r2
1
r1
K
, infolge rot v
r
K
dr
r
r1
K
r2 r1
ln
K
r1
6.4 m / s
Aus der Bernoullischen Gleichung:
pA
pB
2
vB 2
vA2
1.25 104 Pa
c.)
pA
2
pB
v0
vB
v0
2
3
2
n 1 n 1
...
ln 2 n n 2
r
mit n 2
r1
vA
v0
r2
infolge der Kontinuität: vdurchschn.
r1
3.2
4 m / s , vB
2
...
0.
v0
Lösungen
35
4
Impulssatz
4/1
Fx
4/2
Man wende die Bernoullische-Gleichung zwischen den Ein- und Austrittspunkt an, daraus:
w2
a.)
12100 N
w1
v2
15,6 m/s
b.)
73 nach rechts ab v1
c.)
F
d.)
E2
5000N, nach links 30 ab v1
E1
329
m2
s2
4/3
F
510 N , Winkel zwischen F und v ist 45° (’Richtung Nordost’)
4/4
F
109 N
4/5
F
57 N
4/6
G
14 N
4/7
Man schreibe den Impulssatz für die Kontrolloberfläche, die nur die Platte und die obere
Teil des Strahles enthält:
G
A v2
A0 v0 v
für v Eintrittgeschwindigkeit an der Kontrolloberfläche erhält man mit der Anwendung der
Bernoullischen Gleichung:
v
v0 2
v0
4.55 m / s
2 g h
4/8
Mit der Anwendung des Impulssatzes in x und y
Richtung erhält man:
a)
F 636 N
b)
A1 / A2
5.8
Lösungen
36
Geometrische Lösung:
A0 v 2
(infolge von
1 a
52 N
4/10
G
4/11
h 1m
4/12
P
4/13
Fx
Fy
4/14
p1
p1'
p1'
p2
p1
p2
2
123 Pa
p1
p2
(
p1
p2
qV
51 m3 / s
4/15
4/16
4/17
u
A v (v u )
A2 ( p1
h
A2 v 2 )
a
arcsin
4/9
A1 v 2
302 W
280 N
v1 (v1'
1
2
( v2
2)
1
1
2
v1 (v2
p2 )
v1 )
2
v1' )
g h
1
2
v12
v1 )
A2v2 (v2 v1 )
6.5 mm
Die Bernoullische Gleichung zwischen Punkt 1 und 2 liefert (Punkt 2 ist in dem
Ausflussquerschnitt):
v12
2
p1
v2 2
2
p0
g h
, der Querschnitt des Rohres ist konstant, v2
strömende Masse ist inkompressibel,
=konst
v1 , die
Lösungen
37
Eine andere Zusammenhang wäre die Bernoullische Gleichung zwischen Punkt 1 und Punkt
3, (Punkt 3 liegt auf dem Wasserspiegel):
v12
2
v2
p1
p0
v1 und v 3
4/18
h 0.8 m
4/19
h 1m
4/20
v22
2
qV
ohne Platte
qV
mit Platte
0.
2
g h
pB
C
wo
pB
C
2
v2
v3
2
(Borda-Carnotsche-Verlust)
Lösungen
38
5
Hydraulik
dv
dy
5/1
F
A
5/2
p1
p0
72400 Pa
5/3
p1
p0
1500 Pa
5/4
Re
plam
pturb
5/5
plam
pturb
qv d
d2
4
7.5 N
konst
d
qv 2 L 64
2 d 4 2 d konst
d
16
qv 2 L
2 d4 2 d
16
0.316
konst
4
d
qv 2 L 64
2 A2 d qv d
A
qv 2 L 0.316
2 A2 d 4 qv d
A
konst
d4
konst
d5
konst qV
konst qV 1.75
Lösungen
5/6
39
Mit der Voraussetzung der laminaren Strömung, mit
d
64 / Re , erhält man für
13.4 mm . Die Reynoldssche-Zahl ist 189, die unter 2300 liegt, also die Strömung ist
tatsächlich laminar.
5/7
p1
5/8
h 17 mm
5/9
p0
143 Pa
v2
L
1
2
d
g h
Mit der Voraussetzung der laminaren Strömung, die Lösung ist
d 19.3 mm .
Re 33 2300 , also die Strömung ist tatsächlich laminar.
5/10
qv
0.23 m3 / s
5/11
qv
0.0817 m3 / s
5/12
p1
p0
10900 Pa
5/13
p1
p0
28500 Pa
5/14
a)
H
2m
b)
p1
p0
P
77 W
5/15
40000 Pa
Die Drehleistung kann mit der Reduzierung der Ölviskosität oder Erhöhung der Spaltbreite
reduziert werden.
5/16
Die nützliche Höhenunterschied ist hnutz
g hnutz
v2 L
2 d
15 m 12 m
2
Man nehme einen Reibungsfaktor auf,
Re
0.827 .05
1.3 10 6
3.2 10 4
0.02 , vRohr
3m 2 9.81m / s 2
200m
0.02 6
0.05m
0.827 m / s
0.024
Die nächste Iterationschritt liefert vRohr
werden.
3m.
0.755 m / s , und die Iteration kann beendet
Lösungen
40
Um h 12 m zu erreichen, muss die Austrittsgeschwindigkeit des Konfusors minimal:
v2
5/17
2 g h
a)
d2
b)
qv
15.3 m / s sein.
0.755 m / s
50 mm 11 mm
15.3 m / s
1.47 10 3 m3 / s
a) Als erster Schritt kann die reibungsfreie Geschwindigkeit kalkuliert werden:
7 .7 m / s ,
videal
2 g 3m
und A
18
m3 / s
3600
7.7 m / s
6.5 10 4 m 2 .
Also der Rohrdurchmesser ist im reibungsfreien Fall 29 mm. Wegen der Rohrreibung muss
das Rohr einen größeren Durchmesser haben. Man nehme einen Reibungsfaktor und einen
Durchmesser auf:
v
0.02 und d 50 mm :
3m 2 9.81m / s 2
14m
0.02 4 1
0.05m
2.36 m / s
A
21.2 10 4 m 2
d
52 mm
2.36 0.052
9.45 104
0.018
6
1.3 10
(Bei dieser Reynolds-Zahl kann das Rohr als hydraulisch glatt betrachtet werden). Der
Re
nächste Iterationsschritt liefert
0.018 und d 52 mm , man erhält den neuen
Durchmesser von 51.2 mm . Die Iteration kann beendet werden.
b) Wenn der Damm höher ist, kann der Druck im Rohr den Sattdampfdruck erreichen. In
diesem Fall kann die Wassersäule zerreißen. Den niedrigsten Druck nach dem Ventil findet
man in der oberen, rechten Krümmung des Rohres. Aus der Gleichung
pmin
p0
g hmax
2
v2 1
kann hmax berechnet werden.
L1 L2
d
Lösungen
41
6
Gasdynamik
6/1
v2
6/2
qm
6/3
a)
t2 statisch
42 C
b)
t2 gesamt
20 C
T*
T1
2
6/4
260 m / s
A2
10 3 m 2 1.37 kg / m3 200
2v2
0.833
1
a1
R T1
346 m / s
T*
a1
T1
a*
v*
316 m / s
1
*
T
T1
*
6/5
2.9 kg / m3
1
qm
v*
*
A*
0.018 kg / s
qm
A2
2
v2
0.25 kg / s
A*
*
qm
v
d min
6/6
1
a) v2
*
2.34 10 4 m 2
d * 17.3 mm
2
p1
p2
1
2
b) v2
1
Ma
6/8
v
1
0.59
80 m / s
1
1
p1
2
c) v2
6/7
p1
1
1
p2
p1
2
1
0.274 kg / s
Lösungen
42
6/9
tA
56 C
6/10
T2
262 K , Ma2
6/11
a)
d
b)
F
0.77
138 mm
2
A2 v2
2
9.8 103 N