Übungen zur EDV und Biometrie

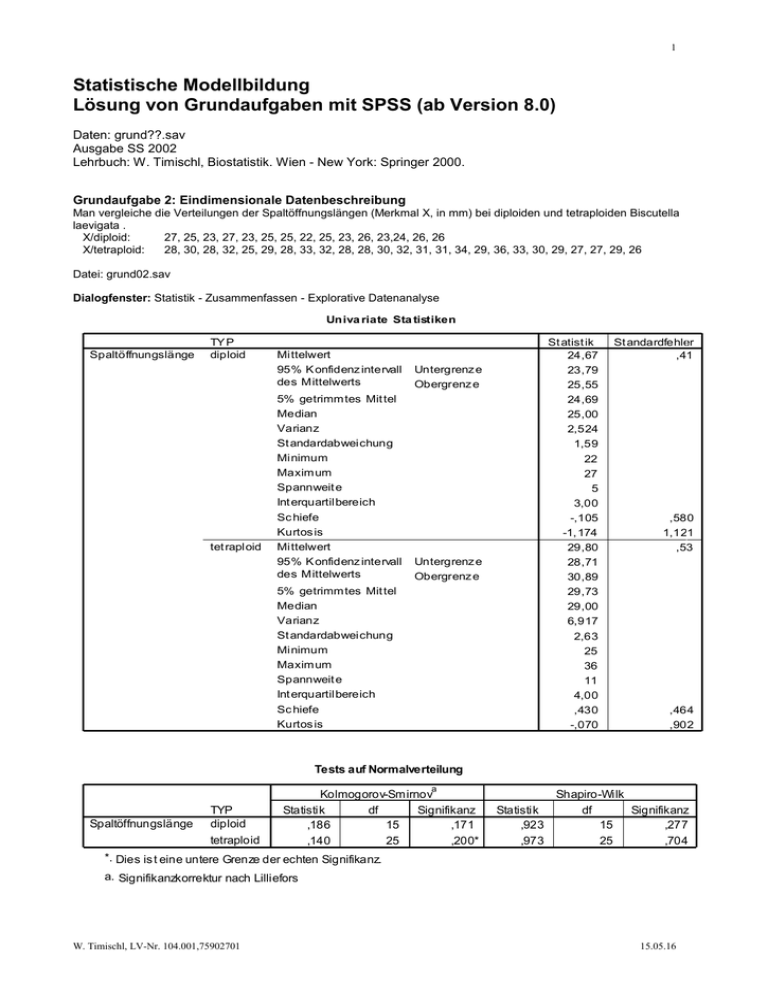
1
Statistische Modellbildung
Lösung von Grundaufgaben mit SPSS (ab Version 8.0)
Daten: grund??.sav
Ausgabe SS 2002
Lehrbuch: W. Timischl, Biostatistik. Wien - New York: Springer 2000.
Grundaufgabe 2: Eindimensionale Datenbeschreibung
Man vergleiche die Verteilungen der Spaltöffnungslängen (Merkmal X, in mm) bei diploiden und tetraploiden Biscutella
laevigata .
X/diploid:
27, 25, 23, 27, 23, 25, 25, 22, 25, 23, 26, 23,24, 26, 26
X/tetraploid:
28, 30, 28, 32, 25, 29, 28, 33, 32, 28, 28, 30, 32, 31, 31, 34, 29, 36, 33, 30, 29, 27, 27, 29, 26
Datei: grund02.sav
Dialogfenster: Statistik - Zusammenfassen - Explorative Datenanalyse
Univa riate Sta tistiken
Spaltöffnungslänge
TY P
diploid
tet raploid
Mittelwert
95% K onfidenz intervall
des Mittelwerts
5% getrimmtes Mit tel
Median
Varianz
St andardabweichung
Minimum
Maximum
Spannweit e
Int erquartilbereich
Sc hiefe
Kurtos is
Mittelwert
95% K onfidenz intervall
des Mittelwerts
St atist ik
24,67
23,79
25,55
24,69
25,00
2,524
1,59
22
27
5
3,00
-,105
-1, 174
29,80
28,71
30,89
29,73
29,00
6,917
2,63
25
36
11
4,00
,430
-,070
Untergrenz e
Obergrenz e
Untergrenz e
Obergrenz e
5% getrimmtes Mit tel
Median
Varianz
St andardabweichung
Minimum
Maximum
Spannweit e
Int erquartilbereich
Sc hiefe
Kurtos is
St andardfehler
,41
,580
1,121
,53
,464
,902
Tests auf Normalverteilung
a
Spaltöffnungslänge
TYP
diploid
tetraploid
Kolmogorov-Smirnov
Statistik
df
Signifikanz
,186
15
,171
,140
25
,200*
Statistik
,923
,973
Shapiro-Wilk
df
Signifikanz
15
,277
25
,704
*. Dies is t eine untere Grenze der echten Signifikanz.
a. Signifikanzkorrektur nach Lilliefors
W. Timischl, LV-Nr. 104.001,75902701
15.05.16
2
38
36
34
32
Spaltöffnungslänge
30
28
26
24
22
20
N=
15
25
di pl oi d
tetra plo id
TYP
Grundaufgabe 3: Vergleich einer Wahrscheinlichkeit mit einem Sollwert (Binomialtest)
Bei einer Blumenzwiebelsorte wird eine Keimfähigkeit von mindestens 75% garantiert. In einer Stichprobe von n=60
keimten 35 Zwiebeln.
(i) Liegt eine signifikante Abweichung vom garantierten Prozentsatz vor? Man prüfe diese Frage auf dem
Signifikanzniveau =5%.
(ii) Welche Fallzahl ist notwendig, um eine Unterschreitung des garantierten Anteils um 0.1 mit einer Sicherheit von
90% feststellen zu können?
a) Daten
Datei: grund3.sav (Gewichtung beachten!)
Anzeige der Daten mit: Statistik -Zusammenfassen - Häufigkeiten
Keimfähigkeit
Gültig
1 (ja)
2 (nein)
Gesamt
Häufigkeit
35
25
60
Prozent
58,3
41,7
100,0
Gültige
Prozente
58,3
41,7
100,0
Kumulierte
Prozente
58,3
100,0
b) H0: p>=0.75, H1: p<0.75
Dialogfenster: Statistik - Nichtparametrische Tests - Binomial
Ergebnis:
1-seit.Sign. = P-Wert = Risiko für irrtümliche Ablehnung von H0 (=0,002) --> H0 ablehnen.
c) Fallzahlenschätzung
z_0.95 = IDF.NORMAL(0.95,0,1) = 1.65 (Transformieren - Berechnen)
z_0.90 = IDF.NORMAL(0.90,0,1) = 1.28
p_0=0.75, delta = 0.1
n = 1/delta**2 *(z_095*SQRT(p*(1-p)) + z_090*SQRT((p+delta)*(1-p-delta)))**2 = 137
W. Timischl, LV-Nr. 104.001,75902701
15.05.16
3
Test auf Binomialverteilung
Keimfähigkeit
Gruppe 1
Gruppe 2
Gesamt
Kategorie
ja
nein
N
35
25
60
Beobachteter
Anteil
,583333
,42
1,00
Testanteil
,75
As ymptotische
Signifikanz
(1-seitig)
,002a,b
a. Nach der alternativen Hypothese ist der Anteil der Fälle in der ersten Gruppe < ,75.
b. Basiert auf der Z-Approximation.
Grundaufgabe 4: Vergleich eines Mittelwerts mit einem Sollwert
In einer Zufallsstichprobe von 24 Probanden wurden die folgenden IQ-Werte bestimmt:
115, 119, 119, 134, 121, 128, 128, 152, 97, 108, 98, 130, 108, 110, 111, 122, 106, 142, 143, 140, 141, 151, 125, 126.
(i) Man erstelle eine geeignete Häufigkeitsverteilung (grafisch) und beschreibe die Verteilung durch die üblichen
deskriptiven Statistiken.
(ii) Man prüfe, ob der durchschnittliche IQ signifikant (= 5%) größer als 130 ist.
a) Häufigkeitsverteilung
Daten: grund04.sav
Dialogfenster: Statistik - Zusammenfassn - Häufigkeiten
Statistiken
IQ
N
Gültig
Fehlend
Mittelwert
Standardfehler des Mittelwertes
Median
Modus
Standardabweichung
Varianz
Schiefe
Standardfehler der Schiefe
Kurtos is
Standardfehler der Kurtosis
Spannweite
Minimum
Maximum
Summe
24
0
123,92
3,20
123,50
108a
15,70
246,34
,109
,472
-,788
,918
55
97
152
2974
a. Mehrere Modi vorhanden. Der kleinste Wert wird angezeigt.
W. Timischl, LV-Nr. 104.001,75902701
15.05.16
4
IQ
10
8
6
Häufigkeit
4
2
Std.abw. = 15,70
Mittel = 123,9
N = 24,00
0
98,5
110,5
122,5
134,5
146,5
IQ
b) Sollwertvergleich
H0: Im Mittel gilt: IQ <= Sollwert = 130
H1: Im Mittel gilt: IQ > Sollwert = 130
Dialogfenster: Statistik - Mittelwerte vergleichen - t-Test bei einer Stichprobe
Statistik bei einer Stichprobe
N
IQ
Mittelwert
123,92
24
Standardfehler
des
Mittelwertes
3,20
Standardabweichung
15,70
Test bei einer Sichprobe
Testwert = 130
IQ
T
-1,899
df
23
Sig.
(2-seitig)
,070
Mittlere
Differenz
-6,08
95% Konfidenzintervall
der Differenz
Untere
Obere
-12,71
,54
Ergebnis:
Wenn - wie in diesem Beispiel - der Stichprobenmittelwert und der Sollwert im Sinne von H0 zueinander stehen: Risiko
für irrtümliche Ablehnung von H0 = 1-(2-seit.Sig)/2 = 96,5% --> H0 nicht ablehnen.
Grundaufgabe 5: Mittelwertvergleich (Parallelversuch - Paarvergleich)
An Hand der Datentabelle sollen folgende Fragen untersucht werden ( = 5%):
(i) Bewirkt das Testpräparat (Präparat=1) eine mittlere Abnahme Fe1-Fe2 der Zielvariablen (Serumeisen) vom
Zeitpunkt 1 (Variable Fe1) bis zum Zeitpunkt 2 (Variable Fe2), die von der durch das Kontrollpräparat (Präparat=2)
verursachten abweicht?
(ii) Zeigt die Zielvariable Serumeisen vom Zeitpunkt 1 (Variable Fe1) bis zum Zeitpunkt 2 (Variable Fe2) im Mittel
innerhalb jeder Präparatgruppe eine signifikante Änderung?
a) Daten
Datei: grund05.sav
Berechnung der Zielvariablen abnahme=Fe1 - Fe2
mit Hilfe von: Transformieren - Berechnen ...
Auflisten der Datentabelle mit Hilfe von: Statistik - Zusammenfassen - Fälle zusammenfassen
W. Timischl, LV-Nr. 104.001,75902701
15.05.16
5
Zusammenfassung von Fällen
Präparat
Test
Kontrolle
1
2
3
4
5
6
7
8
Ins ges amt
1
2
3
4
5
6
7
8
Ins ges amt
N
Mi ttelwert
Standardabweichung
Standardfehler des
Mi ttelwertes
Schiefe
Standardfehler der
Schiefe
Kurtos is
Standardfehler der
Kurtos is
N
Mi ttelwert
Standardabweichung
Standardfehler des
Mi ttelwertes
Schiefe
Standardfehler der
Schiefe
Kurtos is
Standardfehler der
Kurtos is
Fe Zeitp.1
141
137
88
139
54
78
122
62
8
102,62
36,23
Fe Zeitp.2
102
71
90
68
70
64
84
56
8
75,63
15,14
ABNAHME
39
66
-2
71
-16
14
38
6
8
27,00
31,67
12,81
5,35
11,20
-,190
,662
,193
,752
,752
,752
-2,077
-,309
-1,341
1,481
1,481
1,481
123
139
112
115
122
105
105
68
8
111,13
20,66
45
107
91
57
68
47
102
60
8
72,12
24,57
78
32
21
58
54
58
3
8
8
39,00
26,99
7,30
8,69
9,54
-1,210
,445
-,060
,752
,752
,752
2,820
-1,684
-1,451
1,481
1,481
1,481
b) Parallelversuch
b1) Normalitätsprüfung
H0: Daten stammen aus normalverteilter Grundgesamtheit
Datei aufteilen (Daten -Datei aufteilen), um den K-S-Test auf die Zielvariable abnahme in jeder Präparatgruppe
anzuwenden.
Dialogfenster für K-S-Test:
Statistik - Nichtparametrische Tests - K-S bei einer Stichprobe
W. Timischl, LV-Nr. 104.001,75902701
15.05.16
6
Kolmogorov-Smirnov-Anpassungstestc
N
Parameter der Normalverteilunga,b
Extremste Differenzen
Mittelwert
Standardabweichung
Absolut
Positiv
Negativ
Kolmogorov-Smirnov-Z
As ymptotische Signifikanz (2-seitig)
ABNAHME
8
27,00
31,67
,159
,159
-,141
,450
,987
a. Die zu testende Verteilung ist eine Normalverteilung.
b. Aus den Daten berechnet.
c. Präparat = Test
Kolmogorov-Smirnov-Anpassungstestc
N
Parameter der Normalverteilunga,b
Extremste Differenzen
Mittelwert
Standardabweichung
Absolut
Positiv
Negativ
Kolmogorov-Smirnov-Z
As ymptotische Signifikanz (2-seitig)
ABNAHME
8
39,00
26,99
,211
,125
-,211
,596
,869
a. Die zu testende Verteilung ist eine Normalverteilung.
b. Aus den Daten berechnet.
c. Präparat = Kontrolle
b2) t-Test für unabhängige Stichproben
H0: mittl.abnahme/Test = mittl.abnahme/Kontrolle
H1: mittl.abnahme/Test <> mittl.abnahme/Kontrolle
Wichtig: vor Anwendung des t-Tests Aufteilung der Datei aufheben!
(Daten - Datei aufteilen/alle Fälle analysieren)
Dialogfenster für t-Test:
Statistik - Mittelwerte vergleichen - t-Test bei unabhängigen Stichproben
Gruppenstatistike n
Präparat
ABNAHME Test
Kontrolle
W. Timischl, LV-Nr. 104.001,75902701
N
8
8
Mittelwert
27,00
39,00
St andardabweichung
31,67
26,99
St andardfehler
des
Mittelwertes
11,20
9,54
15.05.16
7
Te st bei unabhängige n Stichproben
SE Diff .
14
13,656
,428
,429
-12,00
-12,00
14,71
14,71
O
Mittl. Diff.
-,816
-,816
95% Konf. Int.
Diff.
U
Sign. (2-seit.)
,591
df
,302
T-Test für die Mittelwert gleic hheit
T
Sign.
ABNAHME Varianz. gleich
Varianz. n. gleich
F
Levene-Tes t
-43,55
-43,63
19,55
19,63
Ergebnis:
Risiko für eine irrtümliche Ablehnung von H0 ist
P=2-seit.Sig = 42.8% > 5% --> H0 kann nicht abgelehnt werden!
b3) Bestimmung der Power
Dialogfenster:
Statistik - Allgemeines lineares Modell - GLM-Allgemein mehrfaktoriell (Hinweis: "Power=Beobachtete Schärfe" in
Optionen aktivieren)
Te sts der Zwische nsubjekteffekte
Abhängige Variable: ABNAHME
Quelle
Korr.Modell
Konst. Term
PRAEP
Fehler
Gesamt
Korrigierte
Gesamtvariation
SQ Ty p III
576,000b
17424, 000
576,000
12120, 000
30120, 000
12696, 000
df
1
1
1
14
16
MQ
576,000
17424, 000
576,000
865,714
F
,665
20,127
,665
Sign.
,428
,001
,428
NZP
,665
20,127
,665
a
Power
,119
,986
,119
15
a. Unter Verwendung von Alpha = ,05 berechnet
b. R-Quadrat = ,045 (korrigiert es R-Quadrat = -,023)
Ergebnis: Power (=Schärfe) = 11,9%, d.h.
Sicherheit, mit dem gewählten Versuchsansatz die Differenz der Mittelwerte 27 (Test) und 39 (Kontrolle) der
Zielvariablen "abnahme" als signikant zu erkennen, ist zu klein, um eine Entscheidung für H0 zuzulassen.
--> Versuchsplanung
c) Paarvergleich für das Testpräparat (Vergleich der Zielvariablen Fe1 und Fe2)
Präparatgruppe 1 (Test) auswählen mit:
Daten - Fälle auswählen - Falls Bedingung praep=1 zutrifft
Hypothese:
H0; im Mittel gilt Fe1 = Fe2 gegen H1: im Mittel gilt: Fe1 <> Fe2
Dialogfenster für den t-Test bei gepaarten Stichproben:
Statistik - Mittelwerte vergleichen - t-Test bei gepaarten Stichproben
Statistik bei gepa arte n Stichproben
Paaren
FE, Zeitp.1
FE, Zeitp.2
W. Timischl, LV-Nr. 104.001,75902701
Mittelwert
102,63
75,63
N
8
8
STD
36,23
15,14
SEM
12,81
5,35
15.05.16
8
Te st bei gepa arte n Stichproben
Mittelwert
Paaren
FE
Zeitp.1 FE
Zeitp.2
27,00
Gepaarte Differenz en
95% Konf. int. Diff.
STD
SEM
U
O
31,67
11,20
,52
53,48
T
2,411
Sign.
(2-seit .)
df
7
,047
Ergebnis: P-Wert = 2-seit.Sig = 4.7% < 5% --> H0 ablehnen.
Grundaufgabe 6: Wirksamkeits- u. Äquivalenzprüfung im Rahmen eines Paarvergleichs
In einem als randomisierte Versuchsanlage geplanten Experiment wurden 7 Probanden zeitlich hintereinander zwei
Präparate (1=Test, 2=Kontrolle) verabreicht, wobei die Zuordnung der Probanden zu den Präparatsequenzen 12 bzw. 21
zufällig erfolgte. Die Zielvariable ist die Halbwertszeit HWZ für die Elimination des jeweiligen Präparates aus dem Blut.
Man prüfe (=5%):
(i) Gibt es im Mittel einen Unterschied bezüglich der Zielvariablen (Wirksamkeitsprüfung)?
(ii) Sind die Halbwertszeiten im Mittel gleich? (Äquivalenzprüfung, Gleichheit besteht, wenn sich die Halbwertszeiten um
weniger als 20% des Kontrollpräparates unterscheiden.)
a) Daten
Datei: grund06.sav
Auflisten mit: Statistik - Zusammenfassen - Fälle zusammenfassen
Zusammenfassung von Fällena
1
2
3
4
5
6
7
Ins ges amt
N
Standardabweichung
Standardfehler des
Mittelwertes
Schiefe
Standardfehler der
Schiefe
Kurtosis
Standardfehler der
Kurtosis
Proband-Nr.
1
2
3
4
5
6
7
7
2,16
HWZ -Testpräp.
1,50
1,92
1,43
1,68
1,97
2,01
1,85
7
,2320
HWZ-Kontrolle
,82
8,769E-02
,1459
,000
-,558
,670
,794
,794
,794
-1,200
-1,589
-,713
1,587
1,587
1,587
1,95
2,05
2,46
2,88
2,52
1,80
2,03
7
,3861
a. Begrenzt auf die ersten 100 Fälle.
b) Wirksamkeitsprüfung mit dem t-Test für abhängige Stichproben
H0: Die Halbwertszeiten der Präparate stimmen im Mittel überein
H1: Die Halbwertszeiten der Präparate sind im Mittel verschieden
Dialogfenster: Statistik - Mittelwerte vergleichen - t-Test bei gepaarten Stichproben
W. Timischl, LV-Nr. 104.001,75902701
15.05.16
9
Statistik bei gepa arte n Stichproben
Mittelwert
Paaren
Halbw. zeit
-Testp.
Halbw. zeit Kontr.
N
STD
SEM
1,7657
7
,2320
8,769E-02
2,2414
7
,3861
,1459
Test bei gepaarten Stichproben
Gepaarte Differenzen
Mittel
w.
Paaren
Halbw.zeit
-Testp.
Halbw.zeit
- Kontr.
STD
-,4757
95% CI Differenz
Untere
Obere
SEM
,5025
,1899
-,9405
-1,E-02
T
df
-2,505
Sig.
(2-seitig)
6
,046
Ergebnis: P = 2-seit.Sig. = 4,6% < 5% --> Die beobachtete Mittelwertdifferenz (Test-Kontrolle) von -0.4757 ist
signifikant.
c) Äquivalenzprüfung
H0: absolute Differenz der mittleren Halbwertszeiten >= vorgegebener relevanter Unterschied D (z.B. 20% des Mittels
des Kontrollpräparates)
ind die Präparate äquivalent)
Westlake-Verfahren:
H0 wird auf dem Niveau  abgelehnt (d.h. für die Äquivalenz der Präparate entschieden), wenn das (1-2)Konfidenzintervall der Mittelwertdifferenz im Toleranzintervall (-D, +D) liegt.
Dialogfenster: Statistik - Mittelwerte vergleichen - t-Test bei gepaarten Stichproben
(Konfidenzintervall auf 90% einstellen!)
Te st bei gepa arte n Stichproben
Gepaarte Differenzen
Mittelwert
Paaren
Halbwertsz eit
- Testpräp. Halbwertsz eit
- Kontrollpräp.
-,4757
STD
,5025
SEM
,1899
90% CI der
Differenz
Untere
Obere
-,8448
-,1066
T
-2, 505
Sig.
(2-seit ig)
df
6
,046
Ergebnis:
Stichprobenmittel des Kontrollpräperat ist 2,414; D (=20% von 2,414) = 0,448;
Toleranzintervall für die Äquivalenz = (-0,448, +0,448);
90%-Konfidenzintervall für die Mittelwertdifferenz ist nicht im Toleranzintervall enthalten. --> keine Äquivalenz
Grundaufgabe 7: Chiquadrat-Test für diskrete Verteilungen
Bei einem seiner Kreuzungsversuche mit Erbsen erhielt Mendel 315 runde gelbe Samen, 108 runde grüne, 101 kantige
gelbe und 32 kantige grüne. Sprechen die Beobachtungswerte gegen das theoretische Aufspaltungsverhältnis von
9 : 3 : 3 : 1? ( = 5%)
W. Timischl, LV-Nr. 104.001,75902701
15.05.16
10
a) Daten
Datei: grund07.sav (Gewichtung der Fälle mit freq beachten!)
b) Anpassungstest
H0: die Phänotypen treten mit den Wahrscheinlichkeiten 9/16, 3/16, 3/16, 1/16 auf.
Dialogfenster: Statistik - Nichtparametrische Tests - Chi-quadrat
Phänotyp
rund/gelb
rund/grün
kantig/gelb
kantig/grün
Gesamt
Beobachtetes
N
315
108
101
32
556
Erwartete
Anzahl
312,8
104,3
104,3
34,8
Residuum
2,3
3,8
-3,3
-2,8
Statistik für Test
Chi-Quadrata
df
As ymptotis che Signifikanz
Phänotyp
,470
3
,925
a. Bei 0 Zellen (,0%) werden weniger als 5 Häufigkeiten
erwartet. Die kleinste erwartete Zellenhäufigkeit ist
34,8.
Ergebnis: P = 92,5% --> H0 kann nicht abgelehnt werden.
Grundaufgabe 8: Vergleich von 2 Wahrscheinlichkeiten (unabhängige Stichproben)
Es ist zu untersuchen, ob die Düngung (Mineral- bzw. Tresterkompostdüngung) einen Einfluss auf den Pilzbefall
(Falscher Mehltau) von Weinstöcken (Vitis vinifera) hat oder nicht. Dazu werden 39 mineralgedüngte Weinstöcke
beobachtet, und es wird dabei festgestelltet, dass in 6 Fällen ein starker Befall (Ausprägung 1) zu verzeichnen ist, in den
restlichen 33 Fällen nur ein schwacher bzw. überhaupt keiner (Ausprägung 0). Parallel dazu werden 39
tresterkompostgedüngte Weinstöcke untersucht mit dem Ergebnis, dass in 23 Fällen ein starker Befall (Ausprägung 1)
und in 16 Fällen ein schwacher bis nicht erkennbarer Befall (Ausprägung 0) vorhanden war. ( = 5%)
a) Daten
Datei: grund08.sav (Gewichtung der Fälle mit den beobachteten Häufigkeiten beachten!)
b) Test
H_0: Befallrisiko ist unabhängig von der Düngung
Dialogfenster: Statistik - Zusammenfassen - Kreuztabellen
Pilzbefall * Düngung Kreuztabelle
Pilzbefall
nein
ja
Gesamt
W. Timischl, LV-Nr. 104.001,75902701
Anzahl
Erwartete Anzahl
Anzahl
Erwartete Anzahl
Anzahl
Erwartete Anzahl
Düngung
Mineral
Trester
33
16
24,5
24,5
6
23
14,5
14,5
39
39
39,0
39,0
Gesamt
49
49,0
29
29,0
78
78,0
15.05.16
11
Chi-Quadrat-Tests
W ert
Chi-Quadrat nach
Pearson
a
Kontinuität skorrekt ur
Lik elihood-Quotient
Ex akter Test nach Fisher
Zusammenhang
linear-mit-linear
Anzahl der gült igen Fälle
As ymptotis che
Signifik anz
(2-seitig)
df
15,863
b
14,052
16,656
15,660
1
,000
1
1
,000
,000
1
Ex akte
Signifik anz
(2-seitig)
Ex akte
Signifik anz
(1-seitig)
,000
,000
,000
78
a. W ird nur für eine 2x 2-Tabelle berechnet
b. 0 Zellen (,0%) haben eine erwartete Häufigkeit kleiner 5. Die minimale erwartet e Häufigkeit
ist 14,50.
Symmetrische Maße
Nominal- bzgl.
Nominalmaß
Wert
,451
,451
78
Phi
Cramer-V
Anzahl der gültigen Fälle
Näherungs weis e
Signifikanz
,000
,000
a. Die Null-Hyphothese wird nicht angenommen.
b. Unter Annahme der Null-Hyphothese wird der asymptotische Standardfehler
verwendet.
Grundaufgabe 9: McNemar-Test zum Vergleich von 2 Wahrscheinlichkeiten (abhängige Stichproben)
Bei einer Studie wurde u.a. das Ges.Eiweiß i.S. zu Beginn und am Ende bestimmt. Es ergab sich, dass bei 22
Probanden der Eiweißwert vor und nach Ende der Studie im Normbereich lag, bei 12 Probanden lag der Wert vorher im
Normbereich und nachher außerhalb, bei 7 Probanden vorher außerhalb und nachher im Normbereich und bei 4 vorher
und nachher außerhalb des Normbereichs. Hat sich während der Studie eine signifikante Änderung hinsichtlich des
Normbereichs ergeben? ( = 5%)
a) Daten
Datei: grund09.sav (Gewichtung der Fälle beachten!)
b) Test
H0: p(im Normbereich/vorher-->ausßerhalb/nachher) = p(außerhalb/vorher--> im Normbereich(nachher)
Dialogfenster: Statistik - Nichtparametrische Tests - 2 verbundene Stichproben - McNemar
1& 2
Behandlungsbeginn
1
2
W. Timischl, LV-Nr. 104.001,75902701
Behandlungsende
1
2
22
12
7
4
15.05.16
12
Statistik für Testb
1&2
45
N
Exakte Signifikanz
(2-seitig)
a
,359
a. Verwendetete Binomialverteilung.
b. McNemar-Test
Ergebnis: P = 35,9% --> H0 kann nicht abgelehnt werden.
Grundaufgabe 10: Prüfung auf Abhängigkeit (nominale Daten)
Die Wirksamkeit einer Behandlung wurde einerseits durch den Probanden und andererseits durch den Prüfarzt beurteilt.
Man beschreibe den Zusammenhang zwischen den Beurteilungen mit einem geeigneten Korrelationsmaß. Wie groß sind
die bei einer angenommenen Unabhängigkeit zu erwartenden absoluten Häufigkeiten? Ist die Korrelation signifikant von
Null verschieden? ( = 5%)
a) Daten
Datei: grund10.sav (Gewichtung beachten!)
b) Kreuztabelle mit Abhängigkeitsprüfung
H_0: die Beurteilungen durch den Probanden und durch den Prüfarzt sind unabhängig
Dialogfenster: Statistik - Zusammenfassen - Kreuztabellen
Be urte ilung d. Prüfarz t * Beurteilung d. Proband Kre uzta bell e
Beurteilung
d. Prüfarzt
sehr gut
gut
mäßig
Gesamt
Anzahl
Erwart ete Anzahl
Anzahl
Erwart ete Anzahl
Anzahl
Erwart ete Anzahl
Anzahl
Erwart ete Anzahl
Beurteilung d. Proband
sehr gut
gut
mäßig
23
5
4
14,1
9,4
8,5
7
13
6
11,4
7,6
6,9
3
4
10
7,5
5,0
4,5
33
22
20
33,0
22,0
20,0
Gesamt
32
32,0
26
26,0
17
17,0
75
75,0
Chi-Quadrat-Tests
Wert
Chi-Quadrat nach
Pearson
Likelihood-Quotient
Zusammenhang
linear-mit-linear
Anzahl der gültigen Fälle
As ymptotis che
Signifikanz
(2-seitig)
df
25,215
a
4
,000
24,045
4
,000
17,358
1
,000
75
a. 2 Zellen (22,2%) haben eine erwartete Häufigkeit kleiner 5. Die
minimale erwartete Häufigkeit is t 4,53.
W. Timischl, LV-Nr. 104.001,75902701
15.05.16
13
Symmetrische Maße
Nominal- bzgl.
Nominalmaß
Wert
,580
,410
75
Phi
Cramer-V
Anzahl der gültigen Fälle
Näherungs weis e
Signifikanz
,000
,000
a. Die Null-Hyphothese wird nicht angenommen.
b. Unter Annahme der Null-Hyphothese wird der asymptotische Standardfehler
verwendet.
Grundaufgabe 11: Prüfung auf Abhängigkeit bei metrischen Variablen; lineare Regression
In einer Stichprobe von 10 Frauen wurden der Blutdruck (mm Hg)und das Alter registriert (Daten siehe folgende
Tabelle). Kann man vom Alter im Rahmen eines linearen Regressionsmodells auf den Blutdruck schließen? ( = 5%)
a) Daten
Datei: grund11.sav
Auflisten der Fälle mit: Statistik - Zusammenfassen - Fälle zusammenfassen
Zusammenfassung von Fällena
1
2
3
4
5
6
7
8
9
10
Alter/Jahre
36
57
61
42
46
31
49
27
35
58
Blutdruck
(mm Hg)
123
137
139
127
125
120
125
118
125
140
a. Begrenzt auf die ers ten 100 Fälle.
b) Darstellung der Abhängigkeit im Streudiagramm
Dialogfenster: Grafiken - Streudiagramm
W. Timischl, LV-Nr. 104.001,75902701
15.05.16
14
150
140
Blutdruck (mm Hg)
130
120
110
R-Qu. = 0,8689
20
30
40
50
60
70
A lter/Jahre
Ergebnis:
Beschreibung der Abhängigkeit durch lineares Modell adäquat; Anstieg der Regressionsgerade von Null verschieden.
Frage:
Ist der Anstieg signifikant ungleich Null? (Nur dann hängt der Blutdruck vom Alter ab.)
c) Abhängigkeitsprüfung
c1) Korrelationstest (Pearson)
H0: (Pearson-)Korrelation = 0
Dialogfenster: Statistik - Korrelation - Bivariat ...
Korrelationen
Alter/Jahre
Blutdruck (mm Hg)
Korrelation nach Pearson
Signifikanz (2-s eitig)
N
Korrelation nach Pearson
Signifikanz (2-s eitig)
N
Alter/Jahre
1,000
,
10
,932**
,000
10
Blutdruck
(mm Hg)
,932**
,000
10
1,000
,
10
**. Die Korrelation ist auf dem Niveau von 0,01 (2-seitig) signifikant.
c2) Abhängigkeitsprüfung im Rahmen des Regressionsmodells
H0: Geradenanstieg = 0
Dialogfenster: Statistik - Regression - Linear ...
De skriptive Statistike n
Blutdruck (mm Hg)
Alter/Jahre
W. Timischl, LV-Nr. 104.001,75902701
Mittelwert
127,90
44,20
St andardabweichung
7,91
11,97
N
10
10
15.05.16
15
Koeffizientena
Modell
1
Nicht s tandardis ierte
Koeffizienten
B
Standardfehler
100,679
3,860
,616
,085
(Konstante)
Alter/Jahre
Standardi
sierte
Koeffizien
ten
Beta
,932
T
26,086
7,282
Signifikanz
,000
,000
a. Abhängige Variable: Blutdruck (mm Hg)
Ergebnis: Geradenanstieg (=0.616) signifikant ungleich Null (P = 0,000)
Regressionsgleichung: Blutdruck = 100,679 + 0,616 * Alter
Grundaufgabe 12: 1-faktorielle Varianzanalyse
Globaltest, Homogenitätsprüfung, multiple Mittelwertvergleiche)
Man vergleiche an Hand der Beobachtungsreihen in der folgenden Tabelle die Mg-Konzentration zwischen den
Lösungen 1, 2 und 3. Bestehen zwischen den Lösungen signifikante Mittelwertunterschiede? Man führe die Aufgabe
auch mit den K- und Ca-Konzentrationen durch. ( = 5%)
a) Daten
Datei: grund12.sav
Auflisten der Daten mit: Statistik - Zusammenfassen - Fälle zusammenfassen ...
Zusammenfassung von Fällena
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Ins ges amt
N
Mittelwert
Standardabweichung
Standardfehler des
Mittelwertes
Varianz
Schiefe
Standardfehler der
Schiefe
Kurtos is
Standardfehler der
Kurtos is
Nährlösung
1.5K, 0.75Ca
1.5K, 0.75Ca
1.5K, 0.75Ca
1.5K, 0.75Ca
1.5K, 0.75Ca
1.5K, 0.75Ca
1.5K, 3.75Ca
1.5K, 3.75Ca
1.5K, 3.75Ca
1.5K, 3.75Ca
1.5K, 3.75Ca
1.5K, 3.75Ca
7.5K, 0.75Ca
7.5K, 0.75Ca
7.5K, 0.75Ca
7.5K, 0.75Ca
7.5K, 0.75Ca
7.5K, 0.75Ca
18
2,00
,84
Magnesium
218
185
256
251
241
246
184
161
155
185
203
166
182
216
186
145
125
121
18
190,33
41,49
Kalium
712
716
742
715
910
831
712
698
552
855
659
585
1970
1649
1843
2057
1714
2027
18
1108,17
572,73
Calzium
356
431
619
472
555
564
1121
1031
1148
1045
1073
904
398
415
345
253
222
256
18
622,67
333,63
,20
9,78
134,99
78,64
,706
,000
1721,176
,055
328021,0
,786
111310,2
,517
,536
,536
,536
,536
-1,594
-,851
-1,312
-1,416
1,038
1,038
1,038
1,038
a. Begrenzt auf die ers ten 100 Fälle.
W. Timischl, LV-Nr. 104.001,75902701
15.05.16
16
b) Abhängigkeitsprüfung (Nährlösung --> Zielvariable Mg)
(Deskriptive Statistiken, Globaltest, Homogenitätsprüfung, a priori-Vergleiche, Scheffe-Test)
Deskriptive Statistik
Magnesium
Mittelwe
rt
232,83
175,67
162,50
190,33
N
1.5K, 0.75Ca
1.5K, 3.75Ca
7.5K, 0.75Ca
Gesamt
6
6
6
18
STD
26,89
18,11
38,02
41,49
95%-CI für den
Mittelwert
U
O
204,62
261,05
156,66
194,67
122,60
202,40
169,70
210,96
SEM
10,98
7,39
15,52
9,78
Min
185
155
121
121
Max
256
203
216
256
Te st der Homogenität der Varianz en
Magnesium
Levene-Statistik
2,968
df1
df2
2
15
Signifik anz
,082
Ergebnis: Sign. =0,082  Varianzinhomogenität: nicht signifikant.
ANOVA
Magnesium
Zwischen den
Gruppen
(Kombiniert)
Linearer
Term
Kontrast
Abweic hung
Innerhalb der Gruppen
Gesamt
2
1
1
Mittel der
Quadrate
8388,167
14840, 333
1936,000
12483, 667
15
832,244
29260, 000
17
Quadratsumme
16776, 333
14840, 333
1936,000
df
F
10,079
17,832
2,326
Ergebnis: Sign. (Zwischen den Gruppen)= 0,002  Faktorwirkung ist signifikant.
Kontrast-Koeffizienten
Kontras t
1
2
1.5K,
0.75Ca
1
1
Nährlös ung
1.5K,
3.75Ca
-1
0
7.5K,
0.75Ca
0
-1
Kontra st-Tests
Magnesium
Varianzen sind gleich
Varianzen sind nicht
gleich
W. Timischl, LV-Nr. 104.001,75902701
Kontrast
1
2
1
2
Kontrast
wert
57,17
70,33
57,17
70,33
STF
16,66
16,66
13,23
19,01
T
3,432
4,223
4,320
3,699
df
15
15
8,761
9,000
Sign
(2-seit ig)
,004
,001
,002
,005
15.05.16
Sign
,002
,001
,148
17
Mehrfachvergleiche
Abhängige Variable: Magnes ium
Scheffé-Prozedur
(I) Nährlösung
1.5K, 0.75Ca
1.5K, 3.75Ca
7.5K, 0.75Ca
(J) Nährlös ung
1.5K, 3.75Ca
7.5K, 0.75Ca
1.5K, 0.75Ca
7.5K, 0.75Ca
1.5K, 0.75Ca
1.5K, 3.75Ca
Mittlere
Differenz
(I-J)
Standardfehler
57,17*
16,656
70,33*
16,656
-57,17*
16,656
13,17
16,656
-70,33*
16,656
-13,17
16,656
Signifikanz
,013
,003
,013
,736
,003
,736
95%-Konfidenzintervall
Untergrenze
Obergrenze
11,97
102,37
25,13
115,53
-102,37
-11,97
-32,03
58,37
-115,53
-25,13
-58,37
32,03
*. Die mittlere Differenz ist auf der Stufe .05 signifikant.
Magnesium - Homogene Untergruppen
a
Scheffé-Prozedur
Nährlösung
7.5K, 0.75Ca
1.5K, 3.75Ca
1.5K, 0.75Ca
Signifikanz
N
6
6
6
Untergruppe für Alpha
= .05.
1
2
162,50
175,67
232,83
,736
1,000
Die Mittelwerte für die in homogenen Untergruppen
befindlichen Gruppen werden angezeigt.
a. Verwendet ein harmonis ches Mittel für
Stichprobengröße = 6,000.
Ergebnis (Mittelwertvergleiche): Der Mittelwert auf der Faktorstufe "1.5K, 0.75Ca" weicht signifikant von den anderen
Faktorstufenmitelwerten ab.
Mittelwert-Diagramm
240
220
Mittelwert von Magnesium
200
180
160
140
1.5K, 0.75Ca
1.5K, 3.75Ca
7.5K, 0.75Ca
Nährlösung
W. Timischl, LV-Nr. 104.001,75902701
15.05.16