(SPSS): Kruskal-Wallis-Test Von Personen aus insgesamt 6
Werbung
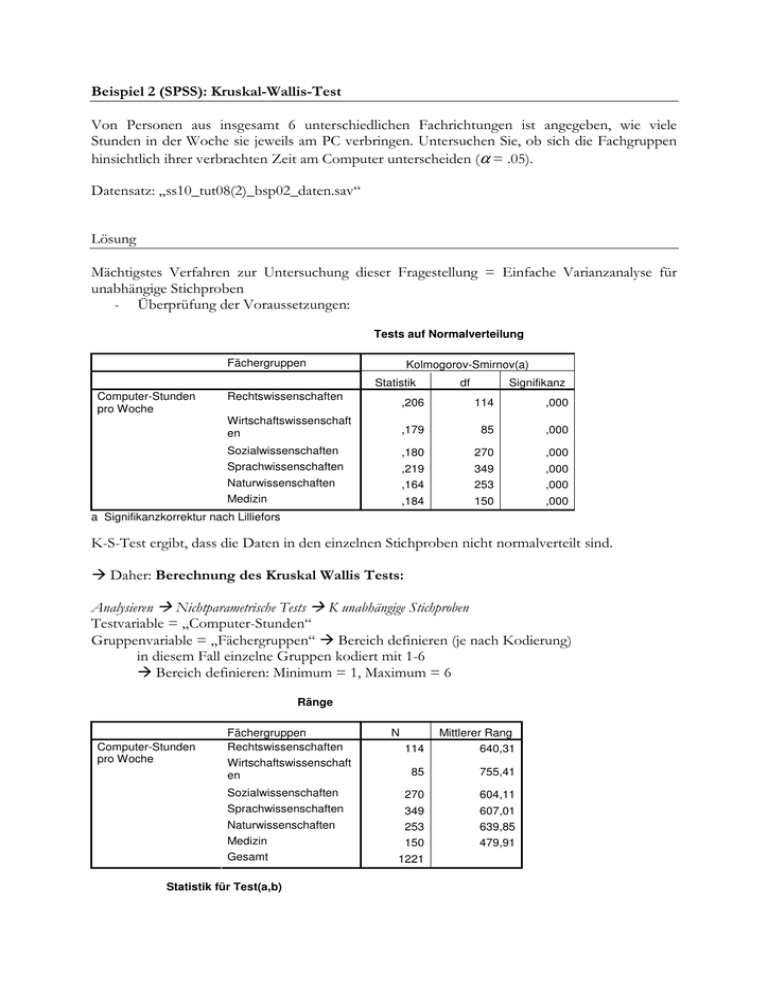
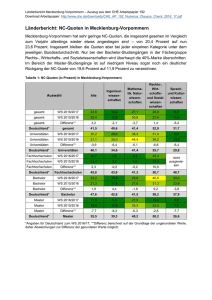
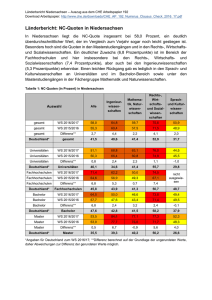
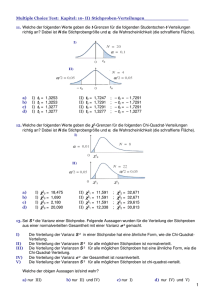
Beispiel 2 (SPSS): Kruskal-Wallis-Test Von Personen aus insgesamt 6 unterschiedlichen Fachrichtungen ist angegeben, wie viele Stunden in der Woche sie jeweils am PC verbringen. Untersuchen Sie, ob sich die Fachgruppen hinsichtlich ihrer verbrachten Zeit am Computer unterscheiden (α = .05). Datensatz: „ss10_tut08(2)_bsp02_daten.sav“ Lösung Mächtigstes Verfahren zur Untersuchung dieser Fragestellung = Einfache Varianzanalyse für unabhängige Stichproben - Überprüfung der Voraussetzungen: Tests auf Normalverteilung Fächergruppen Kolmogorov-Smirnov(a) Statistik Computer-Stunden pro Woche Rechtswissenschaften df Signifikanz ,206 114 ,000 Wirtschaftswissenschaft en ,179 85 ,000 Sozialwissenschaften ,180 270 ,000 Sprachwissenschaften ,219 349 ,000 Naturwissenschaften ,164 253 ,000 Medizin ,184 150 ,000 a Signifikanzkorrektur nach Lilliefors K-S-Test ergibt, dass die Daten in den einzelnen Stichproben nicht normalverteilt sind. Daher: Berechnung des Kruskal Wallis Tests: Analysieren Nichtparametrische Tests K unabhängige Stichproben Testvariable = „Computer-Stunden“ Gruppenvariable = „Fächergruppen“ Bereich definieren (je nach Kodierung) in diesem Fall einzelne Gruppen kodiert mit 1-6 Bereich definieren: Minimum = 1, Maximum = 6 Ränge Computer-Stunden pro Woche Fächergruppen Rechtswissenschaften 114 Mittlerer Rang 640,31 85 755,41 Sozialwissenschaften 270 604,11 Sprachwissenschaften 349 607,01 Naturwissenschaften 253 639,85 Medizin 150 479,91 Gesamt 1221 Wirtschaftswissenschaft en Statistik für Test(a,b) N Chi-Quadrat ComputerStunden pro Woche 37,835 df Asymptotische Signifikanz 5 ,000 a Kruskal-Wallis-Test b Gruppenvariable: Fächergruppen Das Ergebnis ist signifikant Es gibt einen Unterschied zwischen den Fachgruppen hinsichtlich der am Computer verbrachten Zeit.