Multiple Choice Test: Kapitel: 10

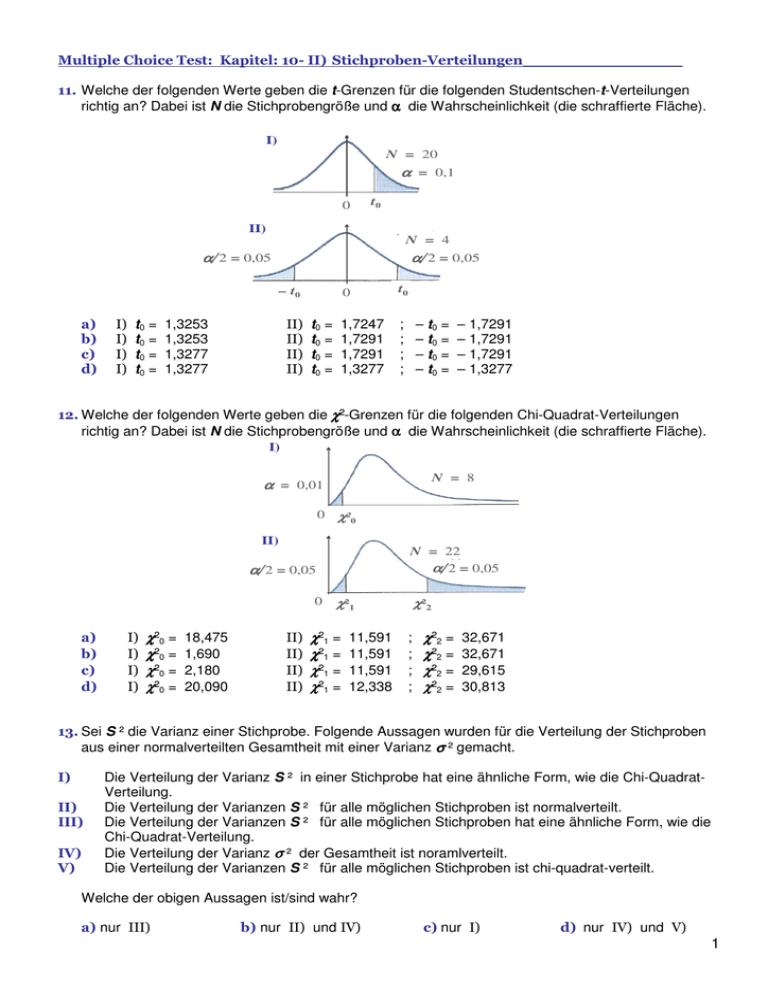
Welche der folgenden Werte geben die t-Grenzen für die folgenden Studentschen-t-Verteilungen
richtig an? Dabei ist N die Stichprobengröße und α die Wahrscheinlichkeit (die schraffierte Fläche).
I)
N = 20
α = 0,1
0
t0
II)
N = 4
α 2 = 0,05
α 2 = 0,05
0
t0
1,7247
1,7291
1,7291
1,3277
;
;
;
;
– t0
t0 =
t0 =
t0 =
t0 =
1,3253
1,3253
1,3277
1,3277
t0 =
t0 =
t0 =
t0 =
– t0 =
– t0 =
– t0 =
– t0 =
– 1,7291
– 1,7291
– 1,7291
– 1,3277
Welche der folgenden Werte geben die χ²-Grenzen für die folgenden Chi-Quadrat-Verteilungen
richtig an? Dabei ist N die Stichprobengröße und α die Wahrscheinlichkeit (die schraffierte Fläche).
I)
N = 8
α = 0,01
0
χ²0
II)
N = 22
α 2 = 0,05
α 2 = 0,05
0
χ²0 =
χ²0 =
χ²0 =
χ²0 =
χ²1
χ²1 =
χ²1 =
χ²1 =
χ²1 =
18,475
1,690
2,180
20,090
11,591
11,591
11,591
12,338
χ²2
;
;
;
;
χ²2 =
χ²2 =
χ²2 =
χ²2 =
32,671
32,671
29,615
30,813
! Sei S ² die Varianz einer Stichprobe. Folgende Aussagen wurden für die Verteilung der Stichproben
aus einer normalverteilten Gesamtheit mit einer Varianz σ ² gemacht.
Die Verteilung der Varianz S ² in einer Stichprobe hat eine ähnliche Form, wie die Chi-QuadratVerteilung.
Die Verteilung der Varianzen S ² für alle möglichen Stichproben ist normalverteilt.
Die Verteilung der Varianzen S ² für alle möglichen Stichproben hat eine ähnliche Form, wie die
Chi-Quadrat-Verteilung.
Die Verteilung der Varianz σ ² der Gesamtheit ist noramlverteilt.
Die Verteilung der Varianzen S ² für alle möglichen Stichproben ist chi-quadrat-verteilt.
Welche der obigen Aussagen ist/sind wahr?
nur
nur
und
nur
nur
und
1
" Sei X die Anzahl der Treffer in einer Stichprobe. Folgende Aussagen wurden für die Verteilung der
Stichproben aus einer Gesamtheit mit einem Anteilswert p gemacht.
Die Verteilung der Treffer X in einer Stichprobe ist binomialverteilt.
Die Verteilung der Treffer X für alle möglichen Stichproben ist binomialverteilt.
Die Verteilung der Anteilswerte für alle möglichen Stichproben ist binomialverteilt.
Welche der obigen Aussagen ist/sind wahr?
nur
nur
alle drei
nur
und
# Sind die Angaben und
wahr oder nur eine oder keine von den beiden?
Sei X die Anzahl der Treffer in einer Stichprobe. Wenn man aus einer Gesamtheit mit einem
Anteilswert p für Treffer Stichproben vom jeweiligen Umfang N zieht, dann ist
I)
II)
der Erwartungswert (Mittelwert) der Verteilung aller möglichen Stichproben für den Treffer X
µ = N ·p.
der Erwartungswert (Mittelwert) der Verteilung aller möglichen Stichproben für den Anteilswert
µp = p.
nur
nur
beide
und
keine von den beiden
$ Sei X die Anzahl der Treffer in einer Stichprobe. Wenn man aus einer sehr großen Gesamtheit mit
einem Anteilswert p für Treffer eine Stichprobe vom Umfang 100 zieht, bei welchem p-Wert ist die
Verteilung der Stichproben-Anteilswerte annähernd normalverteilt?
0,01
0,975
0,15
0,999
% Eine homogene und symmetrische Münze wird 60 mal geworfen. Wie groß ist die Wahrscheinlichkeit,
dass in weniger als 1/3 aller Fälle „Wappen“ erscheint?
0,9957
0,33
0,09
0,0049
& '
()
2