Ergänzungen, Beispiele

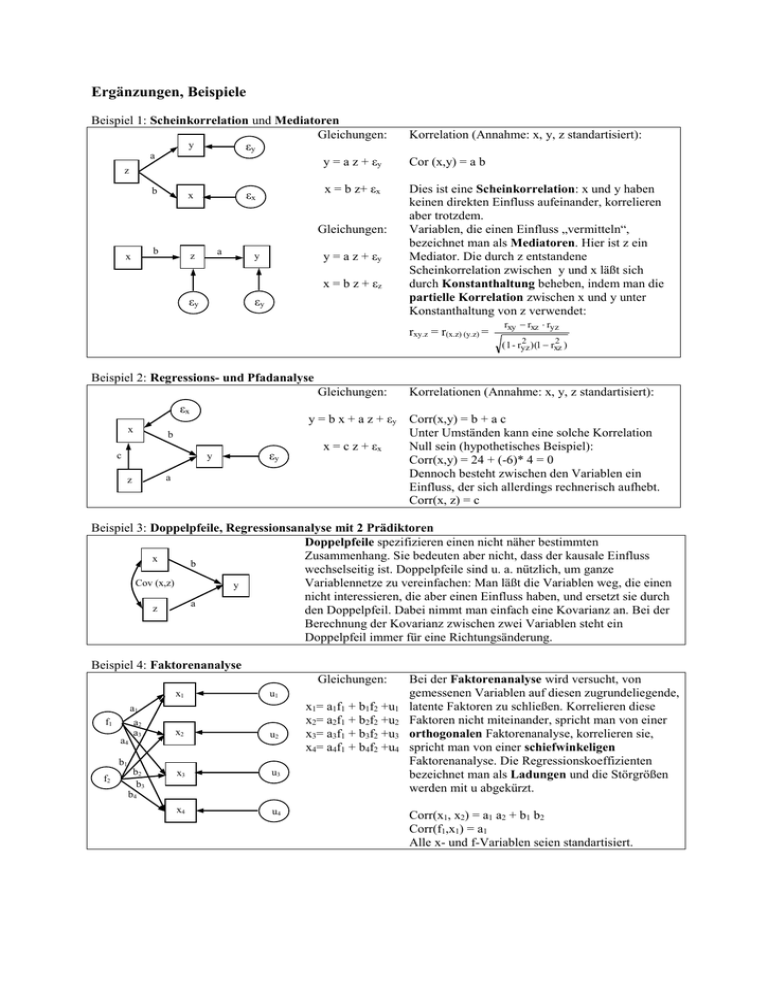
Ergänzungen, Beispiele
Beispiel 1: Scheinkorrelation und Mediatoren
Gleichungen:
y
εy
a
y = a z + εy
z
b
x = b z+ εx
εx
x
Gleichungen:
x
b
a
z
y = a z + εy
y
x = b z + εz
εy
εy
Korrelation (Annahme: x, y, z standartisiert):
Cor (x,y) = a b
Dies ist eine Scheinkorrelation: x und y haben
keinen direkten Einfluss aufeinander, korrelieren
aber trotzdem.
Variablen, die einen Einfluss „vermitteln“,
bezeichnet man als Mediatoren. Hier ist z ein
Mediator. Die durch z entstandene
Scheinkorrelation zwischen y und x läßt sich
durch Konstanthaltung beheben, indem man die
partielle Korrelation zwischen x und y unter
Konstanthaltung von z verwendet:
rxy.z = r(x.z) (y.z) =
rxy  rxz  ryz
2
2
(1 - ryz
)(1  rxz
)
Beispiel 2: Regressions- und Pfadanalyse
Gleichungen:
εx
x
b
c
y
z
εy
a
Korrelationen (Annahme: x, y, z standartisiert):
y = b x + a z + εy Corr(x,y) = b + a c
Unter Umständen kann eine solche Korrelation
x = c z + εx
Null sein (hypothetisches Beispiel):
Corr(x,y) = 24 + (-6)* 4 = 0
Dennoch besteht zwischen den Variablen ein
Einfluss, der sich allerdings rechnerisch aufhebt.
Corr(x, z) = c
Beispiel 3: Doppelpfeile, Regressionsanalyse mit 2 Prädiktoren
Doppelpfeile spezifizieren einen nicht näher bestimmten
Zusammenhang. Sie bedeuten aber nicht, dass der kausale Einfluss
x
b
wechselseitig ist. Doppelpfeile sind u. a. nützlich, um ganze
Cov (x,z)
Variablennetze zu vereinfachen: Man läßt die Variablen weg, die einen
y
nicht interessieren, die aber einen Einfluss haben, und ersetzt sie durch
a
z
den Doppelpfeil. Dabei nimmt man einfach eine Kovarianz an. Bei der
Berechnung der Kovarianz zwischen zwei Variablen steht ein
Doppelpfeil immer für eine Richtungsänderung.
Beispiel 4: Faktorenanalyse
Gleichungen:
x1
f1
a4
a1
a2
a3
u1
x2
u2
x3
u3
x4
u4
b1
f2
b2
b3
b4
x1= a1f1 + b1f2 +u1
x2= a2f1 + b2f2 +u2
x3= a3f1 + b3f2 +u3
x4= a4f1 + b4f2 +u4
Bei der Faktorenanalyse wird versucht, von
gemessenen Variablen auf diesen zugrundeliegende,
latente Faktoren zu schließen. Korrelieren diese
Faktoren nicht miteinander, spricht man von einer
orthogonalen Faktorenanalyse, korrelieren sie,
spricht man von einer schiefwinkeligen
Faktorenanalyse. Die Regressionskoeffizienten
bezeichnet man als Ladungen und die Störgrößen
werden mit u abgekürzt.
Corr(x1, x2) = a1 a2 + b1 b2
Corr(f1,x1) = a1
Alle x- und f-Variablen seien standartisiert.