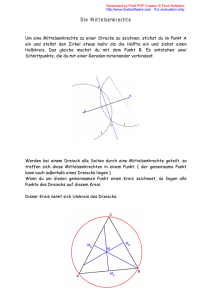
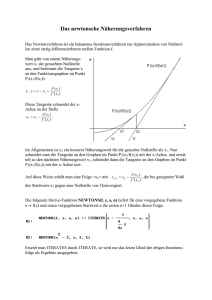
DOC long

Los geht´s (Einführungsbeispiel)
Schriftliche Lösung - lange Version
Öffnen Sie zunächst die Anwendung Graphen &
Geometrie. Drücken Sie
Bildschirm zu erhalten.
, um den dargestellten
Wählen Sie drei Punkte auf der x-Achse.
Die Koordinaten der drei Punkte können dargestellt
werden. Drücken Sie dazu erneut
.
In dem Sie nun die Punkte anklicken, erscheinen
deren Koordinaten
Eine Polynomfunktion oder rationale Funktion, die
diese drei Punkte beinhaltet, soll nun konstruiert
werden.
Zunächst erstellen Sie dafür ein Textfeld (
– 1:
Aktionen, 6: Text). Dies soll die Definition der
Funktion mit den Faktoren enthalten.
Die Buchstaben a, b und c stellen die Nullstellen der
Funktion dar und sind nun Werten zuzuordnen.
Wählen Sie
– Actions – Calculate) und klicken
Sie auf das eben erstellte Textfeld.
Wenn Sie nach der Variablen a gefragt werden,
klicken Sie auf die Koordinaten des ersten Punktes.
Wiederholen Sie diesen Vorgang für die Variablen b
und c.
Wenn Sie nach x gefragt werden, klicken Sie auf die
x-Achse.
Als Resultat erhalten Sie die Funktion, die alle drei
Punkte enthält.
Nun können Sie einen Punkt nehmen
(länger
gedrückt halten) und ihn bewegen. Sie werden
sehen, dass die Funktion sich direkt neu berechnet.
Für einen besseren Überblick lassen wir die
Koordinaten und das Textfeld verschwinden
(Koordinaten und Textfeld jeweils anklicken (rechte
Maus) 2: Auswahl).
Konstruieren Sie die Mittelsenkrechte der beiden
Schnittpunkte des Graphen mit der x- Achse.
Verwenden Sie dafür:
, A: Konstruktion, 3:
Mittelsenkrechte. Klicken Sie nacheinander die
Punkte auf der x Achse an. Vergessen Sie nicht,
diesen Modus mit
zu verlassen.
Greifen Sie das Ende der Mittelsenkrechte (länger
gedrückt halten) und bewegen Sie dieses solange
bis der Schnittpunkt des Graphen mit der
Mittelsenkrechten sichtbar wird.
Konstruieren Sie die Tangente im Schnittpunkt von
Graph und Mittelsenkrechte. Verwenden Sie dafür
, 7: Punkte & Geraden, 7: Tangente. Klicken Sie
zunächst auf den Graphen, dann auf den
Schnittpunkt von Graph und Mittelsenkrechte.
Greifen Sie das Ende der Tangente und verlängern
Sie es. Versichern Sie sich, dass sie den Tangenten
Modus zuvor mit
verlassen haben.
Nun verschieben Sie die Schnittpunkte auf der xAchse.
Die Tangente scheint immer durch den dritten Punkt
zu verlaufen
Wir werden diese Vermutung nun mit CAS
überprüfen.
Fügen Sie die Calculator-Applikation [+page] hinzu.
Die gegebene Funktion f und ihre Ableitung werden
nun definiert (
, 1: Aktionen, 1: Definiere).
Nun benötigen wir den Mittelwert von a und b. Wir
nennen ihn m. Als nächstes wird die Funktion der
Tangente T (x) berechnet.
Nun schauen wir uns die Gleichung der Tangente
an.
Erfüllt der dritte Schnittpunkt die Gleichung?
Tatsächlich, so ist es!