ÜbungszettelSA3_12

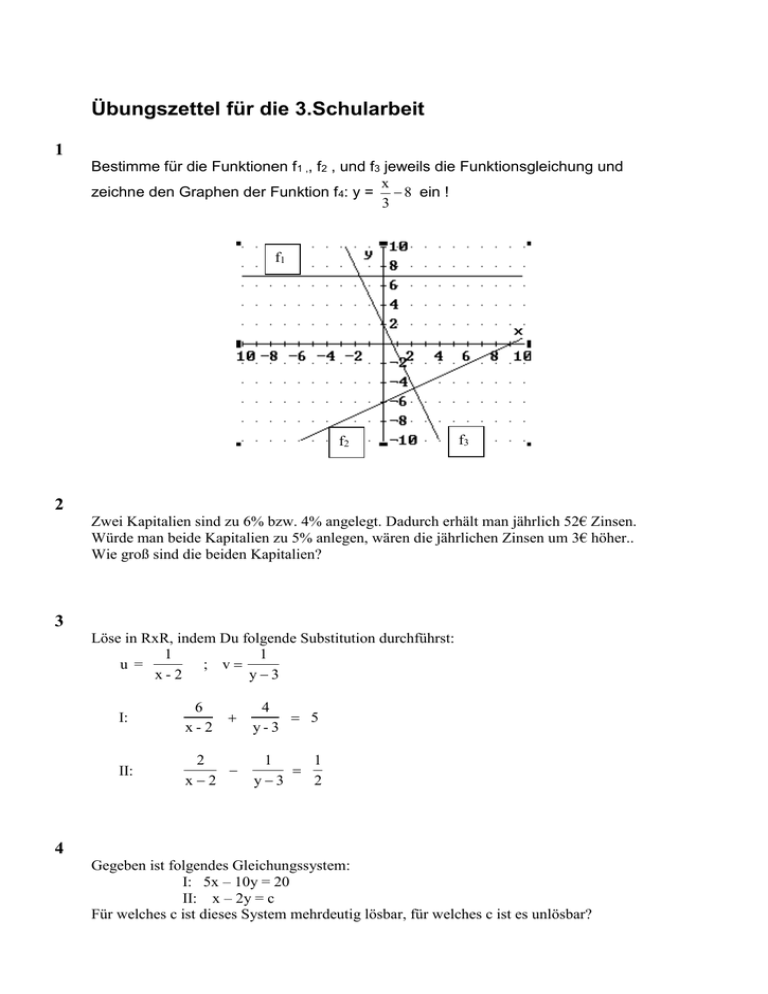
Übungszettel für die 3.Schularbeit
1
Bestimme für die Funktionen f1 ,, f2 , und f3 jeweils die Funktionsgleichung und
x
zeichne den Graphen der Funktion f4: y =  8 ein !
3
f1
f2
f3
2
Zwei Kapitalien sind zu 6% bzw. 4% angelegt. Dadurch erhält man jährlich 52€ Zinsen.
Würde man beide Kapitalien zu 5% anlegen, wären die jährlichen Zinsen um 3€ höher..
Wie groß sind die beiden Kapitalien?
3
Löse in RxR, indem Du folgende Substitution durchführst:
1
1
u =
; v
x-2
y3
I:
6

x-2
4
 5
y-3
II:
2

x2
1
1

y3
2
4
Gegeben ist folgendes Gleichungssystem:
I: 5x – 10y = 20
II: x – 2y = c
Für welches c ist dieses System mehrdeutig lösbar, für welches c ist es unlösbar?
5
Zeichne den Graphen der durch y=
3
x-1 festgelegten Funktion!
2
6
Eine lineare Funktion ist durch ihre Wertetabelle gegeben. Gib ihre Funktionsgleichung an!
x
y
-1 -1,5
0
-1
2
0
7
Löse durch quadratisches Ergänzen: 4x² - 4x - 3 = 0
8
Zerlege die Zahl 55 so in 2 Summanden, dass deren Produkt 666 ergibt!
9
Bestimme Definitions- und Lösungsmenge in R:
5x  3 5x - 3
468


5x - 3 5x  3 25x² - 9
10
Zerlege in Linearfaktoren:
3x² - 14x - 5
11
Löse die Gleichung (x+a)²-b-2=0 nach x auf!
Welche Zahl muss man für b wählen, dass diese Gleichung nur eine Lösung hat?
Welche Zahlen muss man für a und b wählen, damit die Gleichung die Lösungen 1 und -1
hat?
12
Welche quadratische Gleichung hat als Lösungsmenge L = { 1+2 ; 1-2] ?
13
g
t².
2
Wie groß muss v0 sein, dass der Stein genau eine Höhe von 50m erreicht? (g=10 m/s²)
Für den lotrechten Wurf gilt: a=v0.t -
14
Löse in R:
4x2 + 12x + 9 = (3-x)2 + 6
15
lineare Funktionen: entscheide jeweils, ob die Aussage wahr oder falsch ist!
wahr
falsch
wahr
falsch
Es gibt lineare Funktionen, die mehrere Nullstellen besitzen.
Alle Punkte einer linearen Funktion liegen auf einer Geraden.
Jede Gerade der Ebene lässt sich durch eine lineare Funktion beschreiben.
Lineare Funktionen besitzen immer mindestens eine Nullstelle
Direkt proportionale Zusammenhänge lassen sich durch homogene
lineare Funktionen beschreiben.
Für lineare Funktionen gilt stets f(2.x) = 2.f(x.)
Lineare Funktionen f(x) = k.x + d mit d<0 sind streng monoton fallend.
Lineare Funktionen f(x) = k.x + d mit k>0 sind streng monoton steigend.
Lineare Funktionen f(x) = k.x + d mit k>0 und d<0 besitzen eine
Nullstelle mit positiver x-Koordinate.
Für lineare Funktionen f(x) = k.x + d gilt: f(x + Δx) = f(x) + k Δx.
16
quadratische Gleichungen:
Gegeben sind quadratische Gleichungen ax²+bx+c=0 mit a,b,c ε R und a≠0.
Entscheide jeweils, ob die Aussage wahr oder falsch ist!
Jede dieser Gleichungen hat genau zwei reelle Lösungen.
Jede dieser Gleichungen hat maximal zwei reelle Lösungen.
Jede dieser Gleichungen hat maximal zwei verschiedene Lösungen.
Jede dieser Gleichungen hat mindestens eine reelle Lösung.
Es gibt Gleichungen dieser Art, die genau eine Lösung besitzen
Es gibt keine Gleichungen ohne reelle Lösungen
Jede dieser Gleichungen ist immer in folgender Form mit x1,x2 ε R
faktorisierbar: ax²+bx+c=a.(x-x1).(x-x2)
Jede dieser Gleichungen ist immer in folgender Form mit x0,y0 ε R
darstellbar: ax²+bx+c=a.(x-x0)²+y0
17
quadratische Gleichungen:
Welche der folgenden Gleichungen sind auch ohne Lösungsformel lösbar?
Kreuze jeweils an und beschreibe, wie du diese Gleichung ohne Lösungsformel lösen kannst!
x² = 0,81
5x² + 2x . 135 = 0
3x² - 867 = 0
3x² - x = 24
9x² = 25
-14x² + 71x + 33 = 0
x² - 4x + 4 = 0
5x² + 12x = 0
x² = 5x
2x² + 6x = 0
x - 6x + 18 = 0
2x² - 3x = 2