MSA-Vorbereitung

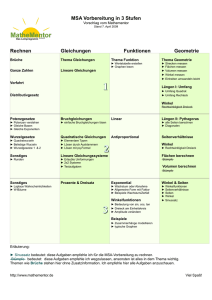
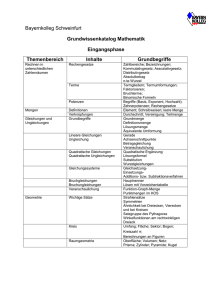
MSA-Vorbereitung
Lineare Funktionen- Lineare Gleichungssysteme
Funktionen


Definition
Darstellungsformen
Lineare Funktion (y=mx+n)


Graph zeichnen
o 2-Punkte
o Achsenabschnitt + Steigungsdreieck
m < 0; m > 0; m = 0; n = 0
Lineare Gleichungssysteme





ax+by=c
(Lineare Gleichung)
y=mx+n
(Funktionsgleichung)
grafisches Lösungsverfahren
rechnerische Verfahren
o Additionsverfahren
o Einsetzungsverfahren
o Gleichsetzungsverfahren
Anzahl der Lösungen eines linearen Gleichungssystems
Textgleichungen mit zwei Unbekannten

Fünf-Schritt-Anleitung
o Festlegung der Variablen
o Gleichungen aufstellen
o Gleichungssystem lösen
o Probe am Text
o Antwortsatz
MSA-Vorbereitung
Quadratische Funktionen und Gleichungen
Quadratische Funktionen


Definition
Darstellungsformen
o Allgemeine Form
o Normalform
o Scheitelpunktform
Graph


Vergleich zur Normalparabel
o Streckfaktor
 verschoben, gestreckt, gestaucht, gespiegelt
o Symmetrieeigenschaften
Punkte auf dem Graph
o Scheitelpunkt
o Nullstellen
o beliebiger Punkt
Umformungen


Scheitelpunktform -> allgemeine Form
Allgemeine Form -> Scheitelpunktform
Quadratische Gleichungen




Lösen/Nullstellenberechnung
Reinquadratische Gleichungen (x²-q=0)
o Wurzelziehen
Quadratische Gleichungen (x²+px=0)
o ausklammern
Allgemeine quadratische Gleichungen (x²+px+q=0)
o Lösungsformel (p-q-Formel)
Der Satz des Vieta

x1+x2 =-p und x1*x2=q
MSA-Vorbereitung
Ähnlichkeit - zentrische Streckung - Strahlensätze
Ähnliche Figuren


Definition
o Winkeltreu
o Gleiche Seitenverhältnisse
o Parallelität bleibt erhalten
Maßstab
o Berechnung
Zentrische Streckung



Streckzentrum und Streckfaktor
Verfahren (Erzeugung ähnlicher Figuren)
o Verkleinern / Vergrößern
o Negativer Streckfaktor
Flächeninhalt (Formel)
Strahlensatz


Strahlensatzfigur
Strahlensätze
o Schenkel
o Abschnitte
o Parallele Abschnitte
Satz des Pythagoras




Rechtwinkliges Dreieck
Kehrsatz des Pythagoras
Berechnung in der Ebene
Berechnung im Raum
MSA-Vorbereitung
Trigonometrie
Berechnung am rechtwinkligen Dreieck


Sinus, Kosinus, Tangens (GAGA-Regel)
Skizze
Berechnung an beliebigen Dreiecken



Sinussatz
Kosinussatz
Merkregel
o Kosinussatz
 SSS (3 Seiten gegeben)
 SWS (2 Seiten und der eingeschlossene Winkel gegeben)
o Sinussatz
 Sonst
Sinus und Kosinus am Einheitskreis




Skizze
Vorzeichen der Sinus und Kosinuswerte
o Winkel zwischen 0° und 90°
o Winkel zwischen 90° und 180°
o Winkel zwischen 180° und 270°
o Winkel zwischen 270° und 360°
Winkel mit negativem Vorzeichen
Winkel mit gleichen Funktionswerten
Bogenmaß

Verhältnis: =
Aufgabe
Bogenmaß b
Winkel α
=
Umfang u
360°
(u = 2π)