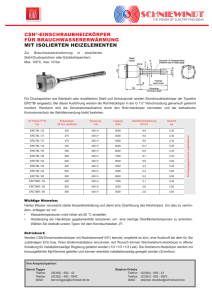
Die zwei Lösungswege haben zu zwei unterschiedlichen

Kopiervorlage
Wo steckt der Fehler?
Das Problem:
Ein Öltank mit 6000 l Fassungsvermögen wird gleichmäßig mit Heizöl gefüllt.
Nach 6 Minuten sind 2100
Liter im Tank, eine Viertelstunde später 4350 Liter.
Wie lange dauert es, bis
der Tank voll ist?
Claras Lösung:
Achims Lösung:
Wegen der Gleichmäßigkeit kann das Phänomen mit
einer linearen Funktion beschrieben werden: y = mx + c.
y bezeichnet das Fassungsvermögen (in l), x die Zeit
(in Minuten). Wegen der Angaben geht das Schaubild
durch die Punkte (6 | 2100) und (21 | 4350). Es gilt:
2100 = 6m + c  c = 2100 – 6 m
4350 = 21m + c  c = 4350 – 21 m
Durch Gleichsetzen folgt:
Nach 6 Minuten sind 2100 l im Tank.
Pro Minute fließen 2100 l : 6 = 350 l in den Tank
In 2 Minuten fließen 2  350 l, in 3 Minuten 3  350 l,
in 4 Minuten 4  350 l, in x Minuten fließen 350x Liter.
2100 – 6m = 4350 – 21m  m = 150
Die gesuchte lineare Funktion ist also g(x) = 350x.
Der Tank ist voll, wenn die 6000 l erreicht worden sind,
d.h. g(x) = 6000.
350x = 6000

Eingesetzt in (1) bekomme ich c = 1200.
Damit ist f(x) = 150x + 1200 die gesuchte lineare Funktion.
Im Tank fehlen noch 6000 l – 4350 l = 1650 l . Ich bestimme nun x , so dass f(x) und 1650 gleich werden:
x=
120
7
oder, anders geschrieben:
x = 17
1
 17,1428
7
150x + 1200 = 1650  150x = 450  x = 3
Sinnvoll gerundet: 17,1
Die Gesamtzeit beträgt damit 6 + 15 + 3 = 24 Minuten.
Die Gesamtzeit beträgt etwa 17,1 Minuten.
Clara und Achim haben zwei unterschiedliche Ergebnisse bestimmt, das kann nicht sein!
Was ist richtig? Was ist falsch? Warum?
PM Heft 2 | April 2005 | 47. Jg., S. 43
© Aulis Verlag Deubner, Köln