21. Januar 2003
Werbung
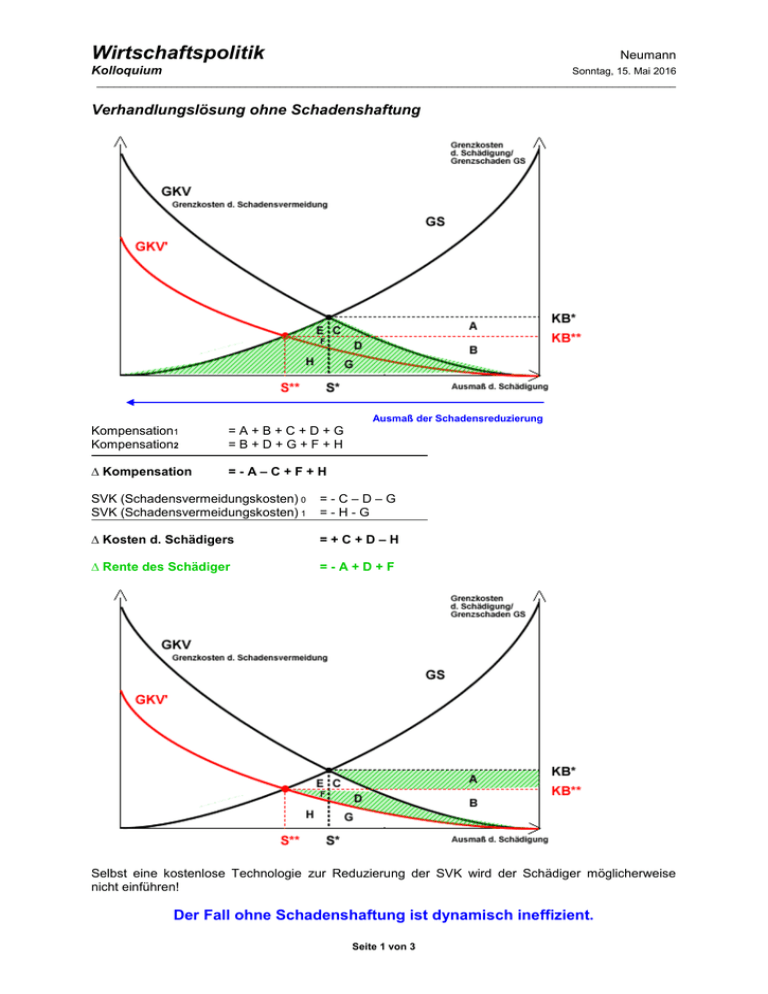
Wirtschaftspolitik Neumann Kolloquium Sonntag, 15. Mai 2016 _____________________________________________________________________________________________________ Verhandlungslösung ohne Schadenshaftung Ausmaß der Schadensreduzierung Kompensation1 Kompensation2 =A+B+C+D+G =B+D+G+F+H ∆ Kompensation =-A–C+F+H SVK (Schadensvermeidungskosten) 0 SVK (Schadensvermeidungskosten) 1 =-C–D–G =-H-G ∆ Kosten d. Schädigers =+C+D–H ∆ Rente des Schädiger =-A+D+F Selbst eine kostenlose Technologie zur Reduzierung der SVK wird der Schädiger möglicherweise nicht einführen! Der Fall ohne Schadenshaftung ist dynamisch ineffizient. Seite 1 von 3 Wirtschaftspolitik Neumann Kolloquium Sonntag, 15. Mai 2016 _____________________________________________________________________________________________________ Problem: ● ● ● ● Zuordnung von Eigentumsrechten Transaktionskosten bei einer Mehrzahl von Geschädigten Verschleierung der Präferenz: Nichtausschließbarkeit => Free – Rider- Verhalten oder bei nur 2 Beteiligten => Monopolproblem Zertifikatslösung (basierend auf dem Coase-Theorem) Faktoren L,A Produktion X,Y Konsumenten A,B 3 Marginalbedingungen: Die wohlfahrtsökonomischen Marginalbedingungen zur Erreichung des Wohlfahrtsoptimums. 1. Marginalbedingung: Die Allokation der Produktionsfaktoren auf die Produktion der Güter soll paretooptimal sein. (effizienter Faktorallokation) 2 exogen gegebene Mengen an Produktionsfaktoren 2 Güter X,Y Produktionsfunktion mit: ● Faktorsubstitution ● abnehmenden Grenzerträgen B ist ineffizient, da mit der selben Menge an Faktoren mehr von X bei gleicher Menge an Y produziert werden könnte. C ist eine paretosuperior zu B. D ist eine paretooptimale Lösung. Auch E ist als Tangentialpunkt paretooptimal! Verbindet man die Kurve paretooptimaler Gütermengenkombinationen, so erhält man die „Kurve effizienter Produktion“ Die Allokation der Faktoren ist genau dann optimal, wenn: Seite 2 von 3 GRSXF GRSYF Wirtschaftspolitik Neumann Kolloquium Sonntag, 15. Mai 2016 _____________________________________________________________________________________________________ 2. Marginalbedingung: Die Aufteilung der Güter auf die Konsumenten soll paretooptimal sein (effiziente Güterallokation) 2 Güter X,Y 2 Konsumenten A,B D ist paretosuperior zu C. E ist effizient Die Verteilung ist dort effizient, wo sich die Indifferenzkurven tangieren. Hier gilt: GRS A GRS B (2. Marginalbedingung erfüllt..!) Die Kurve aller Paretooptima heißt: „Kontraktkurve“. Literaturhinweis: Fritsch/ Wein/ Ewers „Marktversagen und Wirtschaftspolitik“ 3. Marginalbedingung: Es soll ein simultanes Tausch- und Produktionsoptimum vorliegen. Diejenigen Güter sollen produziert werden, die den Präferenzen der Konsumenten entsprechen. Produktionsmöglichkeitskurve/ Transformationskurve Die Punkte auf der Kurve zeigen effizient produzierte Gütermengenkombinationen Seite 3 von 3