Kapitel 9 Anwendungen der Haushaltstheorie Normale, superiore

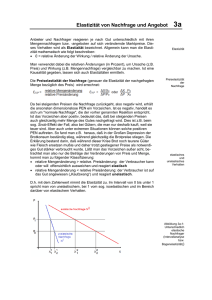
Kapitel 9 Anwendungen der
Haushaltstheorie
Normale, superiore und inferiore
Güter
Zuerst etwas Mathematik: Der Begriff der
Elastizität. Sei y = f(x) eine differenzierbare
Funktion. Sei y´= f´(x)= dy/dx deren erste
Ableitung. Wir unterstellen x>0 und y>0. Dann
lässt sich die Elastizität ε von y bezüglich x
definieren als ε = (dy/y)/(dx/x) = xdy/ydx
=dlogy/dlogx. Die Elastizität ist dimensionslos
und daher von den Maßeinheiten unabhängig.
Einkommenselastizität der Nachfrage nach
einem Gut. Allgemeine Nachfragefunktion:
X = F(Y, P),
wobei P der Preisvektor und X der
Gütervektor ist. Nachfrage nach dem Gut xi:
xi= f (Y;P). Wir untersuchen jetzt xi = f(Y),
wobei die Preise als konstant gedacht sind:
Expansionspfad von xi
Klassifizierung von Gütern nach
ihrer Einkommenselastizität
• Normale Güter
Einkommenselastizität der
Nachfrage nach dem Gut i: ηi
ηi= (dxi/dY)/(xi/Y)
– wenn 0 < ηi <1 Anteil am Einkommen sinkt
• Inferiore Güter
– wenn 0 > ηi Nachfrage geht absolut zurück
• Superiore Güter
– wenn ηi > 1 Anteil am Einkommen steigt
Elastische und unelastische
Nachfragekurve
p
Preiselastizität der Nachfrage
Menge x, Preis p
ε = (dx/dp)/ (x/p) oder dlogx/dlogp
Elastische Nachfrage, wenn |ε| > 1
Unelastische Nachfrage, wenn | ε| < 1
x
1
Kreuzpreiselastizität der
Nachfrage
εij= (∂xi/∂pj)/ (xi/ pj) =
= dlog xi/dlogpj
Ist der Kreuzpreiseffekt negativ,
spricht man von komplementären
Gütern (z.B. Benzin und Autos).
Ist er positiv, spricht man von
Substituten (z.B. Butter und
Margarine)
Einkommens- und Substitutionseffekt einer Preisänderung
x2
.
.
.
x1
Konsum und Freizeit
Freizeit
x2
.. .
Konsum
x1
2