Fragen_Aufgaben_2B

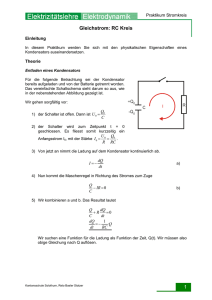
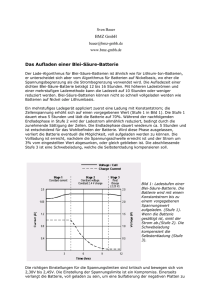
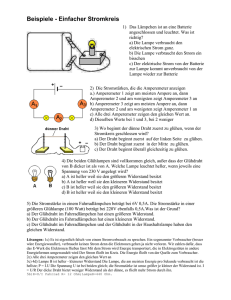
Fragen/Aufgaben 2B
Elektrizität: Leiter, Kondensatoren, Batterien
Fragen
1. Zwischen welchen Grössen erwartet man bei einem Leiter (Widerstand) einen
Zusammenhang? Wie kann man diesen Zusammenhang graphisch darstellen?
2. Was ist eine resistive Charakteristik?
3. Wie sieht eine resistive Charakteristik aus, wenn Stromstärke und Spannung
proportional zueinander sind? Wie kann man den Zusammenhang mathematisch darstellen?
4. Was bedeutet die Steigung der Geraden in einem charakteristischen Diagramm
für ein Widerstandselement, bei dem Strom und Spannung proportional zueinander sind? Wie sieht man den Widerstand des Elementes im Diagramm?
Welche Einheit hat die Steigung der Geraden?
5. Wie sieht die resistive Charakteristik für eine Glühlampe aus (warum ist sie
von der linearen Charakteristik verschieden)? Wie sieht die Charakteristik
einer Diode aus?
6. Wieso ist die über einer Batterie gemessene Spannung nur dann gleich der
„Nennspannung“ (aufgedruckte Spannung), wenn kein Element an die Batterie
angeschlossen ist (wenn wie also keinen geschlossenen Stromkreis haben)?
7. Warum ist die Charakteristik einer Batterie linear (wie im Diagramm von
Aufgabe 6 sichtbar)?
8. Bei der Ausmessung der Charakteristik in Aufgabe 6 wurden die Spannungen
über der Batterie und über dem Lastwiderstand gemessen. Zusätzlich wurde
zwischen Batterie und Lastwiderstand ein Amperemeter geschaltet. Die
Spannungen über Batterie und Lastwiderstand waren bei einer bestimmten
Messung nicht gleich (sie waren 1.257 V und 1.149 V). Wie ist das möglich?
9. Zwischen welchen Grössen erwartet man bei einem Kondensator einen
Zusammenhang?
10. Wie sieht eine kapazitive Charakteristik aus, wenn Spannung und Ladung
proportional zueinander sind? Wie kann man den Zusammenhang mathematisch darstellen?
11. Ein tapischer Kondensator in einer Schaltung ist ein Element mit zwei voneinander getrennten Platten, die entgegengesetzt gleich geladen sind. Also hat
ein Kondensator in einer Schaltung immer die Ladung Null. Trotzdem redet
man (und rechnet man) mit „der Ladung“ eines Kondensators. Was kann
damit gemeint sein?
12. Zwischen welchen Stellen in einem Kondensator tritt die „Kondensatorspannung“ auf?
Aufgaben
1. Zeichnen Sie (mit richtigen Werten) die Charakteristiken von Widerstandselementen mit konstanten Widerstandswerten von 10 , 20  und 40 . Wie
sieht die Charakteristik für negative Spannungen aus?
2. In der Figur ist die gemessene IU-Characteristik einer Glühlampe zu sehen. (a)
Bestimmen Sie den Widerstand in Schritten von 5 V. (b) Man nähert das Temperaturverhalten des elektrischen Widerstands durch die quadratische Formel
(
R(T ) = R20° 1+ a (T - T20° ) + b (T - T20° )
2
)
a = 4.11×10 -3 K -1 , b = 9.62 ×10 -7 K -2
an (R_20° = 1.67 ). Skizzieren Sie den Widerstand als Funktion der
Temperatur (bis etwa 3000 °C). Bestimmen Sie die Temperatur des
Glühdrahtes.
3. Die Charakteristik in Aufgabe 2 kann man ungefähr durch die Funktion
I_Q(U_R) = a·U_R^b annähern (a = 0.258 und b = 0.44). (a) Bestimmen Sie
ein paar Werte der Funktion (z.B. für 2, 4, 8, 16 V). (b) Welche Einheit haben
a und b?
4. Die Lampe von Aufgabe 2 wird an eine Spannungsquelle (Speisegerät mit
fixer Spannung) angeschlossen. Zusätzlich hat es im Stromkreis ein 10 
Widerstandselement (in Serie mit der Lampe). Welche Spannung muss man an
der Quelle einstellen, damit ein Strom der Stärke 0.7 A durch den Stromkreis
fliesst?
5. Das Widerstandselement aus Aufgabe 4 ist parallel zur Lampe geschaltet. Die
Stromstärke durch die Lampe beträgt 0.7 A. Wie gross sind alle Spannungen
und Stromstärken im Stromkreis?
6. Die Charakteristik einer Batterie wurde ausgemessen (wie macht man das?).
Die Daten sind im Diagramm angegeben. Bestimmen Sie die
Leerlaufspannung, den Kurzschlussstrom und den Innenwiderstand der
Batterie.
7. Wenn man 4 der Batterien aus Aufgabe 6 in Serie an die Lampe aus Aufgabe
2 schaltet, wie gross werden dann Spannung über und Strom durch die
Lampe? Bestimmen Sie zuerst die Leerlaufspannung, den Kurzschlusstrom
und den Innenwiderstand der Anordnung der Batterien.
8. Im Stromkreis im Bild befindet sich die Spannungsquelle mit 4.5 V. Anfangs
is das Amperemeter nicht im Stromkreis (später wird es dazugenommen). (a)
Wie gross ist die Spannung über R1? (b) Wie gross ist der Strom durch R4?
(c) Wie gross ist der Strom durch die Spannungsquelle? (d) Nun wird das
Amperemeter dazugeschaltet (Innenwiderstand: 0.50 ). Welche Stromstärke
misst es?
9. Wie gross ist die elektrische Ladung eines 10 µF Kondensators, der auf 100 V
aufgeladen wurde?
10. Ein Kondensator mit Kapazität C wird über einen Widerstand R durch eine
Batterie mit Spannung UB aufgeladen. Wie gross ist die Spannung über dem
Kondensator in dem Moment, wo der Strom die Hälfte des Anfangswertes
beträgt?
11. Ein 1.0 mF Kondensator wird über ein 1000  Widerstandselement entladen.
(a) Wie lange dauert es, bis die Ladung des Kondensators auf 1/e des
Anfangswertes gesunken ist? (b) Wie lange dauert das für die Spannung des
Kondensators und die Stromstärke im Stromkreis? (c) Wie lange dauert es, bis
nur noch die halbe Ladung im Kondensator ist?
Antworten
1. Zwischen Spannung über dem Element und Ladungsstrom durch das Element.
In einem Stromstärke-Spannungs (UR) Diagramm.
2. Der Zusammenhang von Spannung über einem Leiter (Widerstand) und
Ladungsstrom durch den Leiter (Widerstand).
3. Steigende Gerade durch den Ursprung im IQ-UR-Diagramm. IQ = G·UR oder
IQ = 1/R·UR.
4. Steigung entspricht dem Leitwert des Widerstandselementes. Widerstand
entspricht dem Kehrwert der Steigung der Geraden. Einheit der Steigung:
A/V.
5. …
6. Dann fliesst keine Ladung (durch die Batterie). Da die Batterie einen „Innenwiderstand“ hat, fällt das Potential in der Batterie ab, wenn Ladung fliesst, und
dann ist die an den Polen gemessene Spannung kleiner als die „Nennspannung“.
7. Der Abfall des Potentials wegen des „Innenwiderstandes“ is proportional zur
Stromstärke durch die Batterie.
8. Das Amperemeter hat einen (Innen)Widerstand, also fällt das Potential über
dem Element ab (d.h., es hat eine Spannung über dem Element).
9. Zwischen der Ladung des Kondensators und der Spannung über dem Kondensator.
10. Steigende Gerade durch den Ursprung im UC-Q-Diagramm. UC = a·Q oder Q
= C·UC (C = 1/a; a nennt man die Elastanz des Kondensators).
11. Wenn man von „der Ladung“ eines Kondensators spricht, meint man die
Ladung einer der beiden Platten.
12. Die „Kondensatorspannung“ ist die Spannung zwischen den beiden Platten
eines Kondensators.
Lösungen
1. …
2. (a) R(5V) = 10 , etc; (b) T(5V) = 1008°C.
3. A/V^0.44, keine.
4. 10.5 V + 7.0 V = 17.5 V.
5. U = 10 V, I_QL = 0.7 A, I_QR = 1.0 A, I_Q_tot = 1.7 A.
6. Einfacher Stromkreis mit Batterie und (Last)Widerstand; Amperemeter im
Stormkreis und Voltmeter über der Batterie. 4.33 V, 3.46 A, 1.25 .
7. 17.23 V, 3.46 A, 5.0 ; 13.5 V und 0.80 A.
8. (a) 1.83 V. (b) 0.534 A. (c) 0.915 A. (d) 0.496 A.
9. Q = 10^–3 C.
10. UC = 0.5·UB.
11. (a) 1.0 s. (b) Gleich lang. (c) t = tau·ln(2) = 0.693 s.