3_kommentierter_Kompetenzkatalog_Teil_A_und_Cluster_3

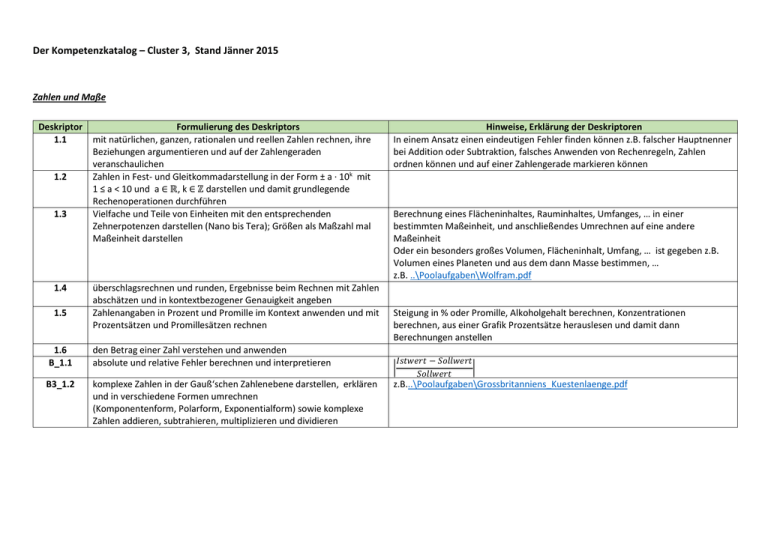
Der Kompetenzkatalog – Cluster 3, Stand Jänner 2015
Zahlen und Maße
Deskriptor
1.1
1.2
1.3
1.4
1.5
Formulierung des Deskriptors
mit natürlichen, ganzen, rationalen und reellen Zahlen rechnen, ihre
Beziehungen argumentieren und auf der Zahlengeraden
veranschaulichen
Zahlen in Fest- und Gleitkommadarstellung in der Form ± a ∙ 10k mit
1 ≤ a < 10 und a ∈ ℝ, k ∈ ℤ darstellen und damit grundlegende
Rechenoperationen durchführen
Vielfache und Teile von Einheiten mit den entsprechenden
Zehnerpotenzen darstellen (Nano bis Tera); Größen als Maßzahl mal
Maßeinheit darstellen
überschlagsrechnen und runden, Ergebnisse beim Rechnen mit Zahlen
abschätzen und in kontextbezogener Genauigkeit angeben
Zahlenangaben in Prozent und Promille im Kontext anwenden und mit
Prozentsätzen und Promillesätzen rechnen
1.6
B_1.1
den Betrag einer Zahl verstehen und anwenden
absolute und relative Fehler berechnen und interpretieren
B3_1.2
komplexe Zahlen in der Gauß‘schen Zahlenebene darstellen, erklären
und in verschiedene Formen umrechnen
(Komponentenform, Polarform, Exponentialform) sowie komplexe
Zahlen addieren, subtrahieren, multiplizieren und dividieren
Hinweise, Erklärung der Deskriptoren
In einem Ansatz einen eindeutigen Fehler finden können z.B. falscher Hauptnenner
bei Addition oder Subtraktion, falsches Anwenden von Rechenregeln, Zahlen
ordnen können und auf einer Zahlengerade markieren können
Berechnung eines Flächeninhaltes, Rauminhaltes, Umfanges, … in einer
bestimmten Maßeinheit, und anschließendes Umrechnen auf eine andere
Maßeinheit
Oder ein besonders großes Volumen, Flächeninhalt, Umfang, … ist gegeben z.B.
Volumen eines Planeten und aus dem dann Masse bestimmen, …
z.B. ..\Poolaufgaben\Wolfram.pdf
Steigung in % oder Promille, Alkoholgehalt berechnen, Konzentrationen
berechnen, aus einer Grafik Prozentsätze herauslesen und damit dann
Berechnungen anstellen
|
𝐼𝑠𝑡𝑤𝑒𝑟𝑡 − 𝑆𝑜𝑙𝑙𝑤𝑒𝑟𝑡
|
𝑆𝑜𝑙𝑙𝑤𝑒𝑟𝑡
z.B...\Poolaufgaben\Grossbritanniens_Kuestenlaenge.pdf
Algebra und Geometrie
Deskriptor
2.1
Formulierung des Deskriptors
rechnen mit Termen
2.2
Rechenregeln für Potenzen mit ganzzahligen und mit rationalen
Exponenten anwenden; Potenz- und Wurzelschreibweise ineinander
überführen
2.3
2.4
Rechengesetze für Logarithmen anwenden
lineare Gleichungen in einer Variablen anwendungsbezogen
aufstellen, lösen, die Lösungen interpretieren und argumentieren
Formeln aus der elementaren Geometrie anwenden, erstellen,
begründen und interpretieren.
2.5
2.6
eine Formel nach einer der variablen Größen umformen und die
gegenseitige Abhängigkeit der Größen in einer Formel interpretieren
und erklären siehe Kommentar
2.7
lineare Gleichungssysteme mit zwei Variablen anwendungsbezogen
aufstellen, lösen und die verschiedenen möglichen Lösungsfälle
argumentieren, interpretieren und grafisch veranschaulichen
lineare Gleichungssysteme mit mehreren Variablen
anwendungsbezogen aufstellen, mithilfe von Technologieeinsatz lösen
und das Ergebnis in Bezug auf die Problemstellung interpretieren und
argumentieren
quadratische Gleichungen in einer Variablen anwendungsbezogen
aufstellen, lösen und die verschiedenen möglichen Lösungsfälle
interpretieren und argumentieren
Exponentialgleichungen vom Typ 𝑎𝑘∙𝑥 = 𝑏 nach der Variablen x
auflösen
Exponentialgleichungen oder Gleichungen mit trigonometrischen
Funktionen in einer Variablen mit Technologieeinsatz auflösen und
das Ergebnis interpretieren
2.8
2.9
2.10
2.11
Hinweise, Erklärung der Deskriptoren z.B
keine Polynomdivision und keine Partialbruchzerlegung
Lineare Gleichung muss in den Grundzügen auch händisch gelöst werden können.
E s werden die Inhalte der elementaren Geometrie vorausgesetzt: Ähnlichkeit, der
Lehrsatz des Pythagoras, Dreiecke, Vierecke, Kreis, Würfel, Quader, gerade
Prismen, gerade Pyramiden, Zylinder, Kegel, Kugel, Längen, Flächen- und
Rauminhalte in anwendungsbezogenen Problemen.
In diesem Deskriptor spiegelt sich auch das Bestimmen der Definitionsmenge, der
Wertemenge wieder.
Formeln können aus allen Gebieten vorkommen, z. B. aus Technik, Wirtschaft und
Naturwissenschaft. Sie müssen nicht im Fachzusammenhang verstanden werden,
dennoch soll die Abhängigkeit der variablen Größen voneinander interpretiert
werden können.
Lineare Gleichungssysteme mit zwei Variablen muss der Schüler auch händisch
lösen können. Eine Möglichkeit das händische Lösen abzufragen, wäre das
Zuordnungsformat 2 aus4, Fehler finden, Multiple Choice 1 aus 5.
Vgl. B_2.1.
2.12
B_2.1
B_2.2
B_2.3
B_2.4
B3_2.5
B3_2.6
Seitenverhältnisse im rechtwinkeligen Dreieck durch Sinus, Cosinus
und Tangens eines Winkels angeben; Seiten und Winkel
anwendungsbezogen berechnen
quadratische Gleichungen in einer Variablen lösen und die
verschiedenen möglichen Lösungsfälle inklusive komplexer Lösungen
interpretieren
Sinus, Cosinus und Tangens eines Winkels 0° ≤ α ≤ 360° (bzw. 0 ≤ α ≤
2π) interpretieren und anhand des Einheitskreises erklären
rechtwinkelige und schiefwinkelige Dreiecke im
anwendungsbezogenen Kontext: modellieren, berechnen,
interpretieren und argumentieren
anwendungsbezogene Exponential- und Logarithmusgleichungen
lösen
Vektoren im ℝ2 und ℝ3: modellieren, berechnen, interpretieren und
argumentieren (Addition, Multiplikation mit einem Skalar,
Skalarprodukt, Vektorprodukt)
lineare Gleichungssysteme in Matrizenform übertragen und diese
Darstellungsform mithilfe der Matrizenmultiplikation begründen
Der Unterschied zu 2.9 ist hier, dass auch das Erkennen komplexer Lösungsfälle
hinzukommt.
z.B. als kontextloses Item, pro Aufgabe darf ein Item kontextlos sein.
Die rechtwinkeligen Dreiecke sind bereits im Teil A abgedeckt. Als Erweiterung ist
hier das schiefwinkelige Dreieck mit den Winkelsätzen zu sehen, sowie
Vermessungsaufgaben (entweder mit einer vorhandenen Skizze rechnen, oder
Skizze selbstständig erstellen, Begriffekatalog beachten).
z.B.: ..\Poolaufgaben\Wuerfel.pdf (Anwendung der Stereometrie, Bezug zu 2.5)
Ist als Erweiterung von 2.10. zu verstehen, bedeutet, dass die Gleichung gegeben
sein muss und damit werden im Anschluss Aufgabenstellungen bearbeitet.
z. B. Gleichgewichtsbedingungen der Statik mit Hilfe von Vektoren angeben und
berechnen.
Resultierende von vektoriellen Größen (Kräfte und Geschwindigkeiten),
Richtungsvektor,
Normalvektor, Betrag, Einheitsvektor, Winkel zwischen Vektoren;
Geradengleichung*, Ebenendarstellung*
Fachbezogene Anwendungen werden in der Aufgabenstellung erklärt.
* wird erst fünf Jahre nach der Einführung des neuen modularen Lehrplans tragend
z.B.: ..\Poolaufgaben,Motoryacht.pdf (Vektordarstellung, Inetrpretation)
Gemeint ist Multiplikation einer Matrix mit einem Spaltenvektor
Funktionale Zusammenhänge
Deskriptor
3.1
3.2.
3.3
3.4
3.5
3.6
3.7
3.8
Formulierung des Deskriptors
eine Funktion als eindeutige Zuordnung erklären und als Modell zur
Beschreibung der Abhängigkeit zwischen Größen interpretieren; den
Graphen einer gegebenen Funktion mit Technologieeinsatz
darstellen, Funktionswerte ermitteln und den Verlauf des Graphen
im Kontext interpretieren
lineare Funktionen anwendungsbezogen modellieren, damit
Berechnungen durchführen, die Ergebnisse interpretieren und damit
argumentieren; den Graphen einer linearen Funktion im
Koordinatensystem darstellen und die Bedeutung der Parameter für
Steigung und Ordinatenabschnitt kontextbezogen interpretieren;
eine lineare Gleichung in zwei Variablen als Beschreibung einer
linearen Funktion interpretieren
Potenzfunktionen (𝑦 = 𝑐 ∙ 𝑥 𝑛 mit n ∈ ℤ, c ∈ ℝ sowie 𝑦 = √𝑥 )
grafisch darstellen und ihre Eigenschaften (Definitions- und
Wertemenge, Symmetrie, Polstelle, asymptotisches Verhalten)
anhand ihres Graphen interpretieren und damit argumentieren
Polynomfunktionen grafisch darstellen und ihre Eigenschaften bis
zum Grad 3 (Null-, Extrem- und Wendestellen, Monotonieverhalten)
interpretieren und damit argumentieren
Exponentialfunktionen grafisch darstellen, als Wachstums- und
Abnahmemodelle interpretieren, die Verdoppelungszeit und die
Halbwertszeit berechnen und im Kontext deuten sowie den Einfluss
der Parameter von Exponentialfunktionen interpretieren
lineare Funktionen und Exponentialfunktionen strukturell
vergleichen, die Angemessenheit einer Beschreibung mittels linearer
Funktionen oder mittels Exponentialfunktionen argumentieren
die Nullstelle(n) einer Funktion gegebenenfalls mit
Technologieeinsatz bestimmen und als Lösung(en) einer Gleichung
interpretieren
Schnittpunkte zweier Funktionsgraphen gegebenenfalls mit
Technologieeinsatz bestimmen und diese im Kontext interpretieren
Hinweise, Erklärung der Deskriptoren z.B
Eine Möglichkeit ist, dass die Funktion mit Technologie erstellt wird (3.1), aber es
ist auch möglich, dass im „Konstruktionsformat“ eine Funktion „händisch“
eingezeichnet werden muss.
die prototypischen Verlaufe der Graphen von f(x) = abx + c mit b ∈ ℝ+ und mit
a, c ∈ ℝ sowie der Graphen von f(x) = a ∙ ℯx + c mit a, c, λ ∈ ℝ kennen; die
Parameter a, b und λ in unterschiedlichen Kontexten deuten
3.9
3.10
B_3.1
B_3.2
B3_3.3
B3_3.41
anwendungsbezogene Problemstellungen mit geeigneten
Funktionstypen (lineare Funktion, quadratische Funktion und
Exponentialfunktion) modellieren
Sinus-, Cosinus- und Tangensfunktionen mit Winkeln im Bogenmaß
grafisch darstellen und die Eigenschaften dieser Funktionen
interpretieren und argumentieren siehe Kommentar
den Zusammenhang zwischen Funktion und Umkehrfunktion
erklären und grafisch als Spiegelung an der 1. Mediane
interpretieren
folgende Funktionen skizzieren, interpretieren und erklären: lineare
Funktion, quadratische Funktion, 1/x, 1/x2, Wurzelfunktion,
Winkelfunktionen, Exponentialfunktion (Wachstums-, Sättigungsund Abklingfunktionen), Logarithmusfunktion; den Einfluss der
Parameter a, b und c interpretieren und erklären (Verschiebung im
Koordinatensystem und Skalierung gemäß a · f(x + b) + c)
die in B3_3.2 genannten Funktionen, Polynomfunktionen sowie die
allgemeine Sinusfunktion (y = a ・ sin(b ・ x + c)) zur
anwendungsbezogenen Modellierung verwenden, mit
Technologieeinsatz berechnen, die Ergebnisse interpretieren und
damit argumentieren
logarithmische Skalierung: modellieren, interpretieren und
argumentieren (Darstellung über mehrere Zehnerpotenzen;
Darstellung von Potenz-, Exponential- und Logarithmusfunktion
als Gerade)
Einfache lineare, quadratische bzw. exponentielle Funktionen müssen auch per
Hand erstellt werden können. Gerade bei den exponentiellen Funktionen auch den
Fall mit zwei beliebigen Punkten (Divisionstrick) beachten.
Einschränkung auf die folgenden Funktionen:
f mit f(x)=sin(x); f mit f(x)=cos(x); f mit f(x)=tan(x)
Das Berechnen der Umkehrfunktion ist hier nicht enthalten, grafisches Ermitteln ja
– eventuell danach daraus Funktionsgleichung ermitteln.
Hier ist eine Funktion vorgegeben und diese wird im Anschluss skizziert,
interpretiert oder erklärt. Es ist aber nicht mit diesem Deskriptor gemeint, dass die
entsprechenden Funktionsgleichungen aus Punkten berechnet werden sollen
Ist allgemein zu verstehen, also auch gültig für z.B. Wurzelfunktion,
Logarithmusfunktion.
z.B.:..\Poolaufgaben\Schwimmstabilitaet.pdf (Funktionsinterpretation)
z. B.: ..\Poolaufgaben\Raketenstart.pdf (quadratische Funktion)
..\Poolaufgaben\Wasserstand_in_einem_Hafenbecken.pdf (allg. Sinusfunktion)
Keine selbstständige Erstellung einer logarithmischen Skala, sondern nur
Herauslesen aus Graphen; begründen, warum Exponential- und
Logaritmenfunktion im logarithmischer Skala lineare Funktionen sind.
z.B.: ..\Poolaufgaben\Der_Schall.pdf (log. Skalierung)
1
Dieser Deskriptor gilt ab dem Maturajahrgang 2017/2018 fur den Cluster 3.
Analysis
Deskriptor
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
B_4.1
B_4.2
B_4.3
B3_4.4
Formulierung des Deskriptors
Grenzwert und Stetigkeit von Funktionen auf der Basis eines
intuitiven Begriffsverständnisses argumentieren
Differenzen- und Differenzialquotient als Änderungsraten
interpretieren, damit anwendungsbezogen modellieren, rechnen
und damit argumentieren
die Ableitungsfunktionen von Potenz-, Polynom- und
Exponentialfunktionen und Funktionen, die aus diesen
zusammengesetzt sind, berechnen siehe Kommentar
Monotonieverhalten, Steigung der Tangente und Steigungswinkel,
lokale Extrema, Krümmungsverhalten, Wendepunkte von
Funktionen am Graphen ablesen, mithilfe der Ableitungen
modellieren, berechnen, interpretieren und argumentieren
den Zusammenhang zwischen Funktion und ihrer Ableitungsfunktion
bzw. einer Stammfunktion beschreiben; in ihrer grafischen
Darstellung interpretieren und argumentieren
Stammfunktionen von Potenz- und Polynomfunktionen berechnen
das bestimmte Integral auf der Grundlage eines intuitiven
Grenzwertbegriffes als Grenzwert einer Summe von Produkten
interpretieren und damit argumentieren
das bestimmte Integral als orientierten Flächeninhalt interpretieren
und berechnen
Ableitungsfunktionen von Winkel- und Logarithmusfunktionen sowie
von zusammengesetzten Funktionen berechnen; Quotientenregel
anwenden
Stammfunktionen von elementaren Winkel- und
Exponentialfunktionen berechnen; Methode der linearen
Substitution anwenden
Eigenschaften von Funktionen: asymptotisches Verhalten bei
Sättigungs- und Abklingfunktionen beschreiben; Unstetigkeitsstellen
interpretieren
Differenzialrechnung im anwendungsbezogenen Kontext anwenden:
modellieren, berechnen, interpretieren und damit argumentieren
siehe Kommentar
Hinweise, Erklärung der Deskriptoren z.B
Weg – Geschwindigkeit – Beschleunigung … dieser Zusammenhang muss bekannt
sein,
Faktorregel, Summenregel, Produktregel, Kettenregel müssen bekannt sein, um
beispielsweise Fehler finden zu können, oder „1 aus 5“, …
Krümmungsverhalten … Bedeutung des Vorzeichens der 2. Ableitung
Es wird nur der Zusammenhang ∫ 𝑣(𝑡)𝑑𝑡 = 𝑠(𝑡) vorausgesetzt; Größe als Integral
ihrer Änderungsrate interpretieren können
das händische Bestimmen der Stammfunktion ist hier auch gemeint für
Fehlersuche etc.
Grundsätzliche Idee: Obersumme, Untersumme
Wird in weiterer Folge in B3_4.5 behandelt
Die Rechenregeln vom Differenzieren werden verglichen mit Teil A noch um die
Quotientenregel erweitert. Die Schüler müssen die Regel händisch anwenden
können, z.B. für Fehlersuche etc.
Können in Form von vorgegebenen fehlerbehafteten Rechenwegen mit
Fehlersuche abgefragt werden.
Hier wird "nur" die Handlungsdimension C abgefragt, nicht das rechnernische
Bestimmen von Unstetigkeitsstellen.
Anwendung der Differenzialrechnung auf die in B_3.2 und B3_3.3 genannten
Funktionstypen;
Linearisierung von Funktionen in einem Punkt;
aus dem Bereich der Physik wird die Kenntnis folgender Zusammenhange
𝑑𝑠
B3_4.5
B3_4.6
Integralrechnung im anwendungsbezogenen Kontext anwenden:
modellieren, berechnen, interpretieren und damit argumentieren
siehe Kommentar
lineare Differenzialgleichungen 1. Ordnung mit konstanten
Koeffizienten anwendungsbezogen aufstellen und lösen; Methode
Trennen der Variablen anwenden; homogene und inhomogene
Differenzialgleichung unterscheiden, allgemeine und spezielle
Losung bestimmen, die Lösungsteile und die Losung darstellen und
interpretieren
𝑑𝑣
𝑑2 𝑠
vorausgesetzt: 𝑠̇ = 𝑑𝑡 , 𝑠̈ = 𝑑𝑡 = 𝑑𝑡 2
z.B.: ..\Poolaufgaben\Harmonische_Schwingung.pdf (alles von oben)
𝑊 = ∫ 𝐹𝑑𝑠, Zusammenhang s-v-a, Ermittlung einer Größe aus ihrer Änderungsrate
durch Integration unter Berücksichtigung einer Anfangsbedingung, Weg als Fläche
der Geschwindigkeitsfunktion erkennen, berechnen und interpretieren.
Anwendung der Integralrechnung auf die in B_3.2 und B3_3.3 genannten
Funktionstypen;
Ermittlung einer Größe aus ihrer Änderungsrate durch Integration unter
Berücksichtigung von Anfangsbedingungen;
das bestimmte Integral (orientierter Flächeninhalt) interpretieren;
aus dem Bereich der Physik wird die Kenntnis folgender Zusammenhange
vorausgesetzt:
𝑠 = ∫ 𝑣𝑑𝑡 und 𝑣 = ∫ 𝑎𝑑𝑡
rotationssymmetrische Volumina
Integralmittelwert: linearer Mittelwert
z.B.: ..\Poolaufgaben\Biegeversuch.pdf (Integration)
Das Aufstellen von Differenzialgleichungen beschränkt sich auf das Übertragen
von angegebenen Zusammenhangen in mathematische Formelsprache.
z.B.: ..\Poolaufgaben\Luftdruck_2.pdf (DGL 1. Ordnung, Polynom 2. Grades B3_3.3)
Stochastik
Deskriptor
5.1
5.2
5.3
5.4
5.5
5.6
B_5.1
B_5.2
B_5.3
Formulierung des Deskriptors
Daten statistisch aufbereiten, Häufigkeitsverteilungen (absolute und
relative Häufigkeiten) grafisch darstellen und interpretieren sowie
die Auswahl einer bestimmten Darstellungsweise
anwendungsbezogen argumentieren
Mittelwerte und Streuungsmaße empirischer Daten berechnen,
interpretieren und argumentieren
die Wahrscheinlichkeit als intuitiven Grenzwert relativer Häufigkeit
interpretieren
die Additionsregel auf einander ausschließende Ereignisse und die
Multiplikationsregel auf unabhängige Ereignisse anwenden;
Zufallsexperimente als Baumdiagramm darstellen
mit der Binomialverteilung modellieren, ihre Anwendung
begründen, Wahrscheinlichkeiten berechnen und die Ergebnisse
kontextbezogen interpretieren
mit der Wahrscheinlichkeitsdichte und der Verteilungsfunktion der
Normalverteilung modellieren, Wahrscheinlichkeiten berechnen*
und die Ergebnisse kontextbezogen interpretieren, Erwartungswert
μ und Standardabweichung σ interpretieren und Auswirkungen auf
die Wahrscheinlichkeitsdichte argumentieren.
den Zusammenhang zwischen der Dichte- und der
Verteilungsfunktion der Normalverteilung beschreiben und erklären
Verteilung der Mittelwerte 𝑥̅ von Stichproben normalverteilter
Merkmalswerte: modellieren, berechnen, interpretieren und
erklären
Schätzwerte für Verteilungsparameter ( μ , σ ) bestimmen;
zweiseitige Konfidenzintervalle für den Erwartungswert μ einer
normalverteilten Zufallsvariablen: modellieren, berechnen,
interpretieren und erklären
Hinweise, Erklärung der Deskriptoren z.B
* Hier sind folgende Varianten gemeint:
– die Wahrscheinlichkeiten für X < k; X > k; k1 < X < k2 bei bekanntem
Erwartungswert und bekannter Standardabweichung berechnen
– aus einer vorgegebenen Wahrscheinlichkeit die Intervallgrenzen für das
Passende Ereignis ermitteln
..\Poolaufgaben\Drehteile_2.pdf (Zusammenhang: 𝜎𝑠 =
𝜎
)
√𝑛
1
𝑛
Schätzwert aus einer Stichprobe vom Umfang n für μ: 𝑥̅ = ∑ 𝑥𝑖 und σ: 𝑠 =
√
1
∑(𝑥𝑖
𝑛−1
− 𝑥̅ )2
Zu unterscheiden sind die Fälle bei unbekannter und bekannter
Standardabweichung:
Die Anwendung der t-Verteilung (im Vergleich zur Normalverteilung) ist bei
unbekannter Standardabweichung σ zur Bestimmung des Vertrauensbereiches für
μ erforderlich (die t-Verteilung wird nur in diesem Zusammenhang benützt).
B_5.4
B3_5.5
lineare Regression und Korrelation: Zusammenhangsanalysen für
anwendungsbezogene Problemstellungen beschreiben und
relevante Größen (Parameter der Funktionsgleichung,
Korrelationskoeffizient nach Pearson) mit Technologieeinsatz
berechnen und interpretieren sowie die Methode der kleinsten
Quadrate erklären.
Ausgleichsfunktionen (linear, quadratisch, kubisch, exponentiell)
modellieren, mit Technologieeinsatz berechnen und die Ergebnisse
interpretieren sowie die Methode der kleinsten Quadrate erklären.
Die Methode der kleinsten Quadrate begrifflich erklären, jedoch keine Berechnung
der Parameter über die partiellen Ableitungen.
z.B.: ..\Poolaufgaben\Fahrzeugtest.pdf (Interpretation von r)
Es ist nur an Technologieeinsatz gedacht, keine Berechnungen von Hand.
z.B.: ..\Poolaufgaben\Fliessgeschwindigkeiten.pdf (quadratisches
Näherungspolynom)