Elementargeometrie Übungsaufgaben, Serie 2 Beweisen Sie die

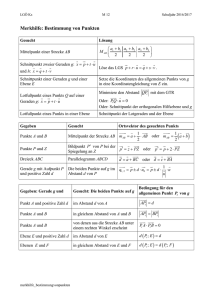
Elementargeometrie
Übungsaufgaben, Serie 2
Beweisen Sie die folgenden Sätze:
Satz 2.1:
Bei einer Bewegung 𝛽 wird
a) jede Gerade auf eine Gerade,
b) jede Strecke auf eine Strecke, deren Endpunkte die Bilder der Endpunkte der
Originalstrecke sind, sowie
c) jede Halbgerade mit einem Anfangspunkt 𝑂 auf eine Halbgerade mit dem Anfangspunkt
𝛽(𝑂) abgebildet.
d) Falls zwei Geraden, Strecken, Halbgeraden oder zwei verschiedene dieser Figuren einen
Punkt 𝑃 gemeinsam haben, so haben die Bildfiguren den Punkt 𝛽(𝑃) gemeinsam.
Satz 2.2:
Bei jeder Bewegung β wird
a) jede Halbebene mit einer Randgeraden 𝑔 auf eine Halbebene mit der Randgeraden 𝛽(𝑔)
und
b) jeder Winkel auf einen kongruenten Winkel sowie das Innere eines beliebigen Winkels
auf das Innere des zugehörigen Bildwinkels abgebildet.
Lösungen:
Satz 2.1:
Es sei 𝛽 eine Bewegung.
a)
Wir gehen von einer Geraden 𝑔 aus. zu zeigen ist, dass das Bild von 𝑔 bei 𝛽 ebenfalls eine Gerade
ist. Hierzu betrachten wir drei paarweise verschiedene Punkte 𝐴, 𝐵 und 𝐶, die alle zu 𝑔 gehören.
Zunächst bestimmen die Bilder von 𝐴 und von 𝐶, also 𝐴′ und 𝐶′ eindeutig eine Gerade. Wenn wir
zeigen können, dass auch der beliebige Punkt 𝐵 auf dieser Geraden liegt, sind wir fertig.
Von drei paarweise verschiedenen Punkten liegt genau einer zwischen den anderen beiden. Es
sei dieses o.B.d.A. der Punkt 𝐵: 𝑍𝑤(𝐴, 𝐵, 𝐶). (ansonsten umbenennen)
Wegen 𝑍𝑤(𝐴, 𝐵, 𝐶) gilt: |𝐴𝐵| + |𝐵𝐶| = |𝐴𝐶|. Wegen der Abstandserhaltung von 𝛽 gilt nun auch
für die Bilder von 𝐴, 𝐵 und 𝐶: |𝐴′𝐵′| + |𝐵′𝐶′| = |𝐴′𝐶′|.
Nach einem bekannten Abstandsaxiom folgt aus der letzten Gleichung die Kollinearität der drei
Punkte 𝐴′ , 𝐵′ und 𝐶′.1 Damit haben wir gezeigt, dass Geraden auf Geraden abgebildet werden.
1
II/3 Für drei beliebige Punkte A, B und C gilt |AB| + |BC| ≥ |AC|.
Falls A, B und C auf einer Geraden liegen, so gilt eine der drei Gleichungen
|AB| + |BC| = |AC|, |AC| + |CB| = |AB|, |BA| + |AC| = |BC|;
ist umgekehrt eine dieser Gleichungen erfüllt, so liegen A, B und C auf einer Geraden.
b)
Wir gehen von einer beliebigen Strecke ̅̅̅̅
𝐴𝐵 aus. Im Beweis von a) haben wir praktisch nebenbei
gezeigt, dass die Zwischenrelation eine Invariante von Bewegungen ist. Hieraus folgt unmittelbar,
dass alle Punkte, die zwischen 𝐴 und 𝐵 liegen, also alle Punkte der offenen Strecke ̅̅̅̅
𝐴𝐵, auf
Punkte, die zwischen den Bildern von 𝐴 und 𝐵 liegen abgebildet werden. Damit wir ̅̅̅̅
𝐴𝐵 auf eine
Strecke abgebildet, wobei die Bilder von 𝐴 und 𝐵 die Endpunkte dieser Bildstrecke sind.
c)
Der Beweis wird ebenfalls mittels der Invarianz der Zwischenrelation geführt.
d)
Es seien 𝑔 und ℎ zwei Geraden, die den Punkt 𝑆 gemeinsam haben.
Fall 1: 𝑔 ≡ ℎ, trivial.
Fall 2: 𝑔 ≢ ℎ
Zunächst können die Bilder von 𝑔 und ℎ nicht parallel sein.
Wäre 𝑔′ ∥ ℎ′, so könnten die beiden Geraden 𝑔′ und ℎ′ zunächst nicht identisch sein. Wären sie
nämlich identisch, so hätten wir unter Beachtung von 𝑔 ≢ ℎ eine Verletzung der Eindeutigkeit
von 𝛽 zu konstatieren.
Somit hätten alle Punkte von 𝑔′ zu ℎ′ einen konstanten positiven Abstand. Diesen positiven
Abstand hätte auch das Bild von 𝑆 auf 𝑔′ zu ℎ′. Im Original wäre dieser Abstand jedoch wegen
𝑆𝜖ℎ gleich 0. Die Abstandserhaltung von 𝛽 wäre damit verletzt.
Die Bildgeraden 𝑔′ und ℎ′ müssen damit genau einen gemeinsamen Punkt haben. Dieser muss
wiederum das Bild von 𝑆 sein.
Unmittelbar einsichtig ist nach dieser Beweisführung auch: 𝑔 ∥ ℎ ⇒ 𝑔′ ∥ ℎ′.
Strecken, Halbgeraden etc. analog unter Beachtung der Invarianz der Zwischenrelation.
Satz 2.2:
a)
Wir betrachten eine beliebige Halbebene 𝑔𝑃+ . Ferner sei 𝑄 ein weiterer Punkt dieser Halbebene.
Da Bild von 𝑔 bei 𝛽wäre die Gerade 𝑔′, 𝑃 würde auf 𝑃′ abgebildet werden. Weil 𝑃 kein Punkt der
Geraden 𝑔 ist, kann 𝑃′ auch kein Punkt der Geraden 𝑔‘ sein. Durch 𝑔‘ und 𝑃′ wird damit
eindeutig eine Halbebene bestimmt: 𝑔′𝑃′+ .
Wenn wir zeigen könnten, dass 𝑄′𝜖𝑔′𝑃′+ gilt, wären wir fertig.
Wir nehmen hierzu an, dass 𝑄′ ∉ 𝑔′𝑃′+ gilt. Aus dieser Annahme würde folgen, dass die Strecke
̅̅̅̅̅̅
𝑄′𝑃′ mit 𝑔′ einen gemeinsamen Punkt hätte. Weil ̅̅̅̅
𝑄𝑃 jedoch keinen Schnittpunkt mit 𝑔 hat.
wäre das nicht möglich.
b)
Wir gehen von dem Winkel ∡𝐴𝑆𝐵 aus. Wegen Strahl auf Strahl und Schnittpunkt auf
Schnittpunkt wird ∡𝐴𝑆𝐵 auf den Winkel ∡𝐴′𝑆′𝐵′ abgebildet.
̅̅̅̅̅̅̅̅ nach SSS
̅̅̅̅̅̅ und 𝐴′𝑆′𝐵′
Wegen der Abstandserhaltung von 𝛽 sind die beiden Dreiecke 𝐴𝑆𝐵
kongruent zueinander. Demzufolge ist ∡𝐴𝑆𝐵 zu seinem Bildwinkel kongruent.
Sei nun 𝑄 ein Punkt aus dem Inneren von ∡𝐴𝑆𝐵. Wir nehmen an, dass 𝑄′ nicht im Inneren von
∡𝐴′𝑆′𝐵′ liegt. Das Innere von ∡𝐴′𝑆′𝐵′ besteht aus allen Punkten, die sowohl zu 𝑆 ′ 𝐴′ , 𝐵′+ als auch
zu 𝑆 ′ 𝐵′ , 𝐴′+ gehören. Unsere Annahme, dass 𝑄′ nicht zum Inneren von ∡𝐴′𝑆′𝐵′ gehört, würde
bedeuten: 𝑄′ gehört nicht zu 𝑆 ′ 𝐵′ , 𝐴′+ oder 𝑄′ gehört nicht zu 𝑆 ′ 𝐴′ , 𝐵′+ . Beides ist wegen
𝑄𝜖𝑆𝐴, 𝐵+ und 𝑄𝜖𝑆𝐵, 𝐴+ entsprechend des bereits bewiesenen Teils a) nicht möglich.