ANWEN_2 - Strahlensatz

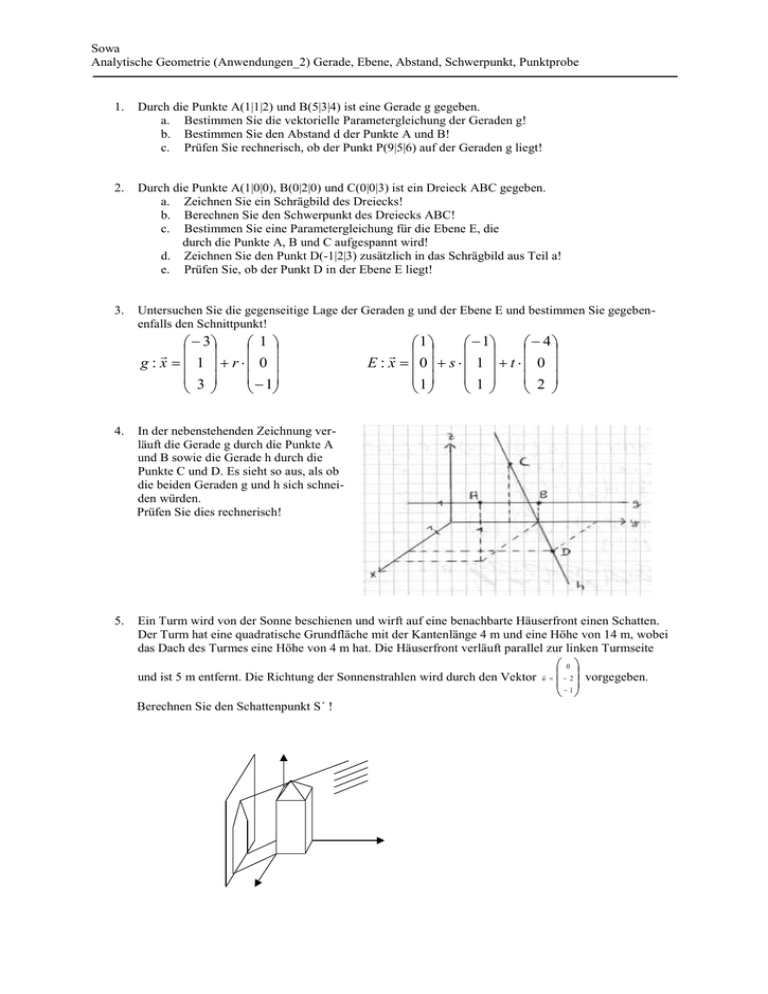
Sowa
Analytische Geometrie (Anwendungen_2) Gerade, Ebene, Abstand, Schwerpunkt, Punktprobe
1.
Durch die Punkte A(1|1|2) und B(5|3|4) ist eine Gerade g gegeben.
a. Bestimmen Sie die vektorielle Parametergleichung der Geraden g!
b. Bestimmen Sie den Abstand d der Punkte A und B!
c. Prüfen Sie rechnerisch, ob der Punkt P(9|5|6) auf der Geraden g liegt!
2.
Durch die Punkte A(1|0|0), B(0|2|0) und C(0|0|3) ist ein Dreieck ABC gegeben.
a. Zeichnen Sie ein Schrägbild des Dreiecks!
b. Berechnen Sie den Schwerpunkt des Dreiecks ABC!
c. Bestimmen Sie eine Parametergleichung für die Ebene E, die
durch die Punkte A, B und C aufgespannt wird!
d. Zeichnen Sie den Punkt D(-1|2|3) zusätzlich in das Schrägbild aus Teil a!
e. Prüfen Sie, ob der Punkt D in der Ebene E liegt!
3.
Untersuchen Sie die gegenseitige Lage der Geraden g und der Ebene E und bestimmen Sie gegebenenfalls den Schnittpunkt!
  3
1
 
  
g : x   1   r  0 
 3
  1
 
 
 1
  1
  4
 
 
  
E : x   0  s   1   t   0 
 1
1
 2 
 
 
 
4.
In der nebenstehenden Zeichnung verläuft die Gerade g durch die Punkte A
und B sowie die Gerade h durch die
Punkte C und D. Es sieht so aus, als ob
die beiden Geraden g und h sich schneiden würden.
Prüfen Sie dies rechnerisch!
5.
Ein Turm wird von der Sonne beschienen und wirft auf eine benachbarte Häuserfront einen Schatten.
Der Turm hat eine quadratische Grundfläche mit der Kantenlänge 4 m und eine Höhe von 14 m, wobei
das Dach des Turmes eine Höhe von 4 m hat. Die Häuserfront verläuft parallel zur linken Turmseite
und ist 5 m entfernt. Die Richtung der Sonnenstrahlen wird durch den Vektor
Berechnen Sie den Schattenpunkt S´ !

u 
0
  2  vorgegeben.
  1
Sowa
Analytische Geometrie (Anwendungen_2) Gerade, Ebene, Abstand, Schwerpunkt, Punktprobe
Lösungen:
1.a
2.b
 1
 4
 
  
g : x   1   r 2 
 2
 2
 
 
S ( 13 | 23 | 1)
2.c
1.b
d  24  4,9
1.c P liegt auf g für r = 2
1
  1
  1




  
E : x   0   s 2   t  0 
 0
 0 
 3 
 




2.d
D liegt in der Ebene E
3.
r = -1; s = 1; t = 1; S (4 | 1 | 4)
4.
A( 4 | 3 | 3); B(0 | 3 | 1); C (0 | 2 | 3); D(3 | 5 | 0)
 4
  4
 



g : x   3   r 0 
 3
  2
 


 0
 3 
 



h : x   2   s 3 
 3
  3
 


g und h schneiden sich nicht
5. A(4/0/0), B(4/4/0), C(0/4/0), E(4/0/10), F(4/4/10), G(0/4/10), S(2/2/14)
 2
 0 


  
gs : x   2   s   2
14 
 1
 


 0 
1
 0

 
 
 
E : x    5  t  0   u  0 
 0 
 0
1


 
 
 2
 0   0 
1
 0



 

 
 
 2   s   2     5  t  0   u  0 
14 
 1  0 
 0
1



 

 
 
Schnittpunkt:
S´ (2 /-5 / 10,5)