1.SA (6C)

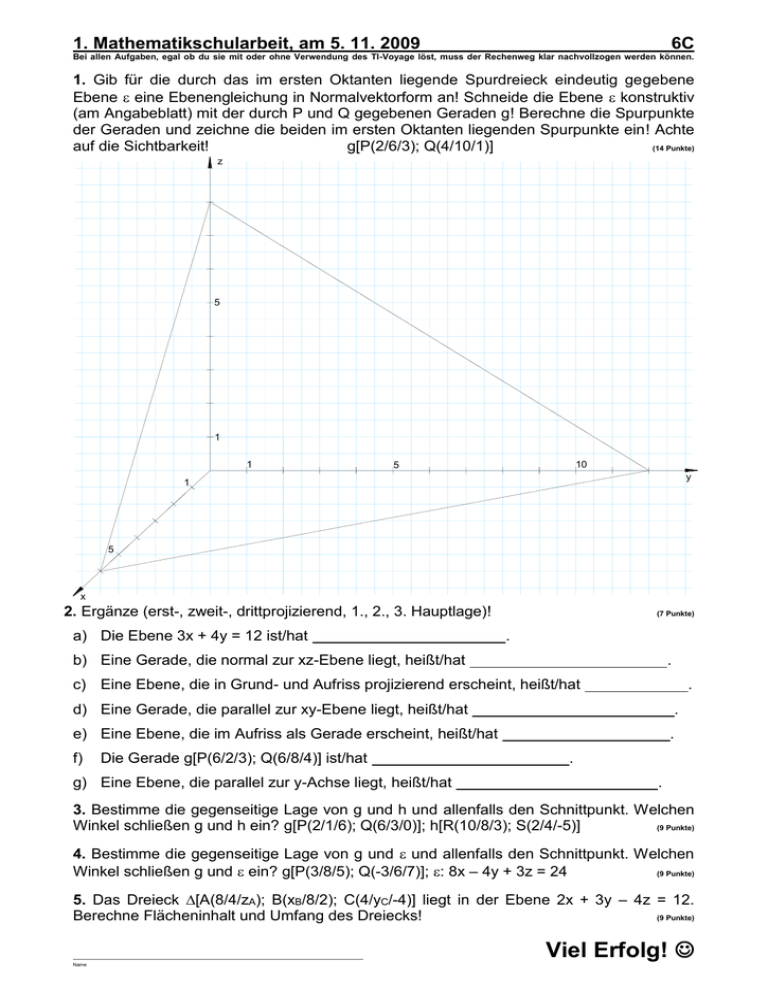
1. Mathematikschularbeit, am 5. 11. 2009
6C
Bei allen Aufgaben, egal ob du sie mit oder ohne Verwendung des TI-Voyage löst, muss der Rechenweg klar nachvollzogen werden können.
1. Gib für die durch das im ersten Oktanten liegende Spurdreieck eindeutig gegebene
Ebene  eine Ebenengleichung in Normalvektorform an! Schneide die Ebene  konstruktiv
(am Angabeblatt) mit der durch P und Q gegebenen Geraden g! Berechne die Spurpunkte
der Geraden und zeichne die beiden im ersten Oktanten liegenden Spurpunkte ein! Achte
auf die Sichtbarkeit!
g[P(2/6/3); Q(4/10/1)]
(14 Punkte)
z
5
1
1
10
5
y
1
5
x
2. Ergänze (erst-, zweit-, drittprojizierend, 1., 2., 3. Hauptlage)!
a) Die Ebene 3x + 4y = 12 ist/hat
(7 Punkte)
.
b) Eine Gerade, die normal zur xz-Ebene liegt, heißt/hat
.
c) Eine Ebene, die in Grund- und Aufriss projizierend erscheint, heißt/hat
.
d) Eine Gerade, die parallel zur xy-Ebene liegt, heißt/hat
.
e) Eine Ebene, die im Aufriss als Gerade erscheint, heißt/hat
f)
Die Gerade g[P(6/2/3); Q(6/8/4)] ist/hat
g) Eine Ebene, die parallel zur y-Achse liegt, heißt/hat
.
.
.
3. Bestimme die gegenseitige Lage von g und h und allenfalls den Schnittpunkt. Welchen
Winkel schließen g und h ein? g[P(2/1/6); Q(6/3/0)]; h[R(10/8/3); S(2/4/-5)]
(9 Punkte)
4. Bestimme die gegenseitige Lage von g und  und allenfalls den Schnittpunkt. Welchen
Winkel schließen g und  ein? g[P(3/8/5); Q(-3/6/7)]; : 8x – 4y + 3z = 24
(9 Punkte)
5. Das Dreieck [A(8/4/zA); B(xB/8/2); C(4/yC/-4)] liegt in der Ebene 2x + 3y – 4z = 12.
Berechne Flächeninhalt und Umfang des Dreiecks!
(9 Punkte)
Viel Erfolg! 
Name