TEP Hall-Effekt in p-Germanium mit dem Cobra4 Mobile

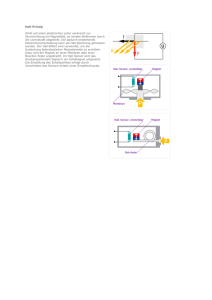
Hall-Effekt in p-Germanium mit dem Cobra4 MobileLink
TEP
Verwandte Begriffe
Halbleiter, Bandtheorie, verbotene Zone, Eigenleitfähigkeit, Störstellenleitfähigkeit, Valenzband,
Leitungsband, Lorentzkraft, magnetischer Widerstand, Mobilität, Leitfähigkeit, Bandlücke, HallKoeffizient.
Prinzip
An einer quaderförmigen Germaniumprobe werden Widerstand und Hall-Spannung in Abhängigkeit von
der Temperatur und vom Magnetfeld gemessen. Aus den Messwerten werden die Bandlücke, die
spezifische Leitfähigkeit sowie die Art und Beweglichkeit der Ladungsträger bestimmt.
Material
1
1
1
1
2
1
1
1
1
1
1
1
3
2
2
1
Cobra4 Mobile-Link, inkl. Akkus, SD-Speicherkarte, USB-Kabel und
„measure“ Software
Cobra4 Sensor Tesla, magnetische Feldstärke, Auflösung max. ±
0,01 mT
Hall-Effekt-Modul
Hall-Effekt, p-Ge, Trägerplatine
Spule, 600 Windungen
Eisenkern, U-förmig, geblättert
Polschuhe, plan, 30 x 30 x 48 mm, 2
Hall-Sonde, tangential, mit Schutzkappe
Netzgerät 0-12 V DC/6 V, 12 V AC
Dreifuß PHYWE
Stativstange PHYWE, 4 Kanten, l = 250 mm
Doppelmuffe PHYWE
Verbindungsleitung, l = 500 mm, rot
Verbindungsleitung, l = 500 mm, blau
Verbindungsleitung, l = 750 mm, schwarz
Digitalmultimeter 2010
12620-55
12652-00
11801-00
11805-01
06514-01
06501-00
06489-00
13610-02
13505-93
02002-55
02025-55
02040-55
07361-01
07361-04
07362-05
07128-00
Abb. 1: Versuchsaufbau
www.phywe.com
P2530162
PHYWE Systeme GmbH & Co. KG © All rights reserved
1
TEP
Hall-Effekt in p-Germanium mit dem Cobra4 MobileLink
Aufgaben
1. Die
Hall-Spannung
wird
bei
Raumtemperatur
und
konstantem
Magnetfeld
in
Abhängigkeit
vom
Steuerstrom gemessen und in einem
Diagramm dargestellt (Messung ohne
Kompensation der Fehlspannung).
2. Die Hall-Spannung über der Probe wird bei
Raumtemperatur
und
konstantem
Steuerstrom in Abhängigkeit von der
magnetischen Flussdichte B gemessen.
3. Die Spannung über der Probe wird bei Abb. 2: Hall-Effekt in einer quaderförmigen Probe. Das
konstantem Steuerstrom in Abhängigkeit Vorzeichen der angezeigten Hall-Spannung gilt, wenn
von der Temperatur gemessen. Basierend die Ladungsträger negativ geladen sind.
auf den Messungen wird die Bandlücke von
Germanium berechnet.
4. Die Hall-Spannung UH wird in Abhängigkeit von der magnetischen Flussdichte B bei
Raumtemperatur gemessen. Das Vorzeichen der Ladungsträger und die Hall-Konstante RH, die
Hall-Beweglichkeit der Ladungsträger μH und die Ladungsträgerkonzentration p werden
basierend auf den Messungen berechnet.
5. Die Hall-Spannung UH wird in Abhängigkeit von der Temperatur bei konstanter magnetischer
Flussdichte B gemessen und die Werte werden in einem Diagramm dargestellt.
Aufbau und Durchführung
Der Versuchsaufbau ist in Abb. 1 dargestellt. Führen Sie die Probe auf der Trägerplatine über die
Führungsnut in das Hall-Effekt-Modul ein. Schließen Sie das Modul über den AC-Eingang auf der
Modulrückseite direkt an den 12 V~-Ausgang des Netzgeräts an.
Führen Sie die Trägerplatine sehr vorsichtig an den Magneten heran, um den Kristall nicht zu
beschädigen. Vermeiden Sie es, die Trägerplatine zu biegen.
Die Hall-Spannung und die Spannung über der Probe werden mit einem Multimeter gemessen.
Verwenden Sie dazu die Buchsen auf der Vorderseite des Moduls. Stromstärke und Temperatur lassen
sich problemlos von dem integrierten Display des Moduls ablesen.
Verwenden Sie zur Messung des Magnetfelds die Cobra4 Sensor-Unit Tesla und die Hall-Sonde, die wie
in Abb. 1 dargestellt direkt in die Nut des Moduls eingesetzt werden kann. Sie können so sicherstellen,
dass der Magnetfluss direkt an der Ge-Probe gemessen wird.
Aufgabe 1
Stellen Sie für das Magnetfeld einen Wert von 250 mT ein, indem Sie die Spannung und Stromstärke
des Netzgeräts ändern. Verbinden Sie das Multimeter mit den Buchsen für die Hall-Spannung (UH) auf
der Vorderseite des Moduls. Schalten Sie das Display des Moduls auf den Stromstärkemodus um.
Bestimmen Sie die Hall-Spannung in Abhängigkeit von der Stromstärke in einem Bereich von -30 mA bis
30 mA in Schritten von ca. 5 mA. Als Ergebnis erhalten Sie eine typische Messung wie in Abb. 3.
Aufgabe 2
Stellen Sie einen Steuerstrom von 30 mA ein. Verbinden Sie das Multimeter mit den Buchsen für die
Probenspannung auf der Vorderseite des Moduls. Bestimmen Sie die Probenspannung in Abhängigkeit
von der positiven magnetischen Flussdichte B bis zu einem Wert von 300 mT. Als Ergebnis erhalten Sie
einen typischen Graphen wie in Abb. 4.
2
PHYWE Systeme GmbH & Co. KG © All rights reserved
P2530162
Hall-Effekt in p-Germanium mit dem Cobra4 MobileLink
TEP
www.phywe.com
P2530162
PHYWE Systeme GmbH & Co. KG © All rights reserved
3
TEP
Hall-Effekt in p-Germanium mit dem Cobra4 MobileLink
Aufgabe 3
Achten Sie darauf, dass die Anzeige während der Messung im Temperaturmodus ist. Stellen Sie
zunächst eine Stromstärke von 30 mA ein. Das Magnetfeld ist ausgeschaltet. Die Stromstärke bleibt
während der Messung nahezu konstant, während sich die Spannung in Abhängigkeit von der
Temperatur ändert. Schalten Sie die Anzeige nun auf den Temperaturmodus um. Starten Sie die
Messung, indem Sie die Heizspule mit Hilfe des EIN/AUS-Schalters auf der Rückseite des Moduls
aktivieren. Bestimmen Sie die Spannungsänderung in Abhängigkeit von der Temperaturänderung für
einen Temperaturbereich von Raumtemperatur bis maximal 140°C. Sie erhalten einen typischen
Kurvenverlauf, wie er in Abb. 5 dargestellt ist.
Aufgabe 4
Stellen Sie eine Stromstärke von 30 mA ein. Verbinden Sie das Multimeter mit den Buchsen für die HallSpannung (UH) auf der Vorderseite des Moduls. Bestimmen Sie die Hall-Spannung in Abhängigkeit von
der magnetischen Flussdichte. Beginnen Sie mit -300 mT, indem Sie die Polarität des Spulenstroms
umkehren, und erhöhen Sie die magnetische Flussdichte in Schritten von ca. 20 mT. Im Nullpunkt
müssen Sie die Polarität ändern. In Abb. 6 ist eine Beispielmessung dargestellt.
Aufgabe 5:
Stellen Sie die Stromstärke auf 30 mA und die magnetische Flussdichte auf 300 mT. Bestimmen Sie die
Hall-Spannung in Abhängigkeit von der Temperatur. Schalten Sie die Anzeige auf den
Temperaturmodus um. Starten Sie die Messung, indem Sie die Heizspule mit Hilfe des EIN/AUSSchalters auf der Rückseite des Moduls aktivieren. Als Ergebnis erhalten Sie eine Kurve wie in Abb. 7.
Theorie und Auswertung
Wenn ein Strom I durch einen leitenden Streifen mit rechteckigem Querschnitt fließt und durch den
Streifen im rechten Winkel zur Stromrichtung ein Magnetfeld verläuft, wird zwischen zwei Punkten auf
gegenüberliegenden Seiten des Streifens eine Spannung, die sogenannte Hall-Spannung, erzeugt.
Dieses Phänomen lässt sich auf die Lorentzkraft zurückführen: die Ladungsträger, die den Strom durch
die Probe hervorrufen, werden im Magnetfeld B in Abhängigkeit von ihrem Vorzeichen und ihrer
Geschwindigkeit v abgelenkt:
(F = auf die Ladungsträger wirkende Kraft, e = Elementarladung).
Da sich negative und positive Ladungsträger in Halbleitern in entgegengesetzter Richtung bewegen,
werden sie in dieselbe Richtung abgelenkt.
Die Art der Ladungsträger, die den Stromfluss bewirken,
kann daher basierende auf der Polarität der HallSpannung bestimmt werden, wenn die Richtung des
Stromflusses und die Richtung des Magnetfelds bekannt
sind.
Aufgabe 1
Abb. 3 zeigt, dass zwischen der Stromstärke I und der
Hall-Spannung UH eine lineare Beziehung besteht:
mit α = Proportionalitätsfaktor.
4
Abb. 3: Hall-Spannung in Abhängigkeit von der
Stromstärke
PHYWE Systeme GmbH & Co. KG © All rights reserved
P2530162
Hall-Effekt in p-Germanium mit dem Cobra4 MobileLink
TEP
Aufgabe 2
Die Widerstandsänderung der Probe aufgrund
des Magnetfelds hängt mit einer Verringerung
der
mittleren
freien
Weglänge
der
Ladungsträger zusammen. In Abb. 4 ist die
nicht-lineare,
eindeutig
quadratische
Widerstandsänderung
bei
steigender
Feldstärke dargestellt.
Aufgabe 3
Im Bereich der Eigenleitfähigkeit haben wir
Abb. 4: Änderung des Widerstands in Abhängigkeit von
der magnetischen Flussdichte
mit σ = Leitfähigkeit, Eg = Energie der
Bandlücke, k = Boltzmann-Konstante, T =
absolute Temperatur.
Wenn der Logarithmus der Leitfähigkeit gegen
T-1 aufgetragen wird, ergibt sich eine Gerade mit
einer Steigung, über die Eg bestimmt werden
kann. Basierend auf den Messwerten in Abb. 5
hat die Steigung der Regressionsgeraden
den folgenden Wert:
mit einer Standardabweichung sb = •±0,07 ・
103 K. (Da die Messung bei konstanter
Stromstärke erfolgten, können wir s ~ U–1 Abb. 5: Kehrwert der Probenspannung in
setzen, wobei U die Spannung über der Probe Abhängigkeit vom Kehrwert der absoluten
ist.)
Temperatur (Da I während der Messung konstant
war, gilt U–1~σ und der Graph entspricht daher
einer Darstellung der Leitfähigkeit als Funktion des
Da
Kehrwerts der Temperatur).
erhalten wir
Aufgabe 4
Mit den in Abb. 2 dargestellten Richtungen des Steuerstroms und des Magnetfelds werden die
Ladungsträger, die den Strom in der Probe hervorrufen, zur Vorderseite der Probe hin abgelenkt. Wenn
also (in einer n-dotierten Probe) Elektronen die vorherrschenden Ladungsträger sind, wird die
Vorderseite negativ, während sie bei der Defektelektronenleitung in einer p-dotierten Probe positiv wird.
Die Leitfähigkeit s0, die Beweglichkeit der Ladungsträger μH und die Ladungsträgerkonzentration p sind
www.phywe.com
P2530162
PHYWE Systeme GmbH & Co. KG © All rights reserved
5
TEP
Hall-Effekt in p-Germanium mit dem Cobra4 MobileLink
über die Hall-Konstante RH miteinander verbunden:
Abb. 6 zeigt eine lineare Beziehung zwischen der HallSpannung und dem B-Feld. Basierend auf den Werten
aus Abb. 6 hat die Regressionsgerade mit der Formel
eine Steigung b = 0,125 VT–1,
Standardabweichung sb •± 0,003 VT–1.
mit
einer
Die Hall-Konstante RH wird daher gemäß
Abb. 6: Hall-Spannung in Abhängigkeit von der
magnetischen Flussdichte
mit der Probendicke d = 1 ・ 10–3m und I = 0,030 A zu
mit der Standardabweichung
Die Leitfähigkeit bei Raumtemperatur berechnet sich aus der Probenlänge l, dem Probenquerschnitt A
und dem Probenwiderstand R0 (vergleiche 2) wie folgt:
Basierend auf den Messwerten
erhalten wir
σ0 = 57,14 Ω–1 m–1.
Die Hall-Beweglichkeit μH der Ladungsträger kann nun bestimmt werden mit
Basierend auf den oben angegebenen Messwerten erhalten wir:
Die Defektelektronenkonzentration p von p-dotierten Proben errechnet sich aus
6
PHYWE Systeme GmbH & Co. KG © All rights reserved
P2530162
Hall-Effekt in p-Germanium mit dem Cobra4 MobileLink
TEP
Unter Verwendung des Werts der Elementarladung
e = 1,602 ・10–19 As
erhalten wir
p = 14,9 ・1020 m–3.
Aufgabe 5
Abb. 7 zeigt zunächst eine Verringerung der
Hall-Spannung bei steigender Temperatur. Da
die Messungen bei konstanter Stromstärke
erfolgten, ist anzunehmen, dass dies auf eine
Erhöhung der Anzahl der Ladungsträger
(Übergang von Störstellenleitfähigkeit zur
Eigenleitfähigkeit)
und
der
damit
einhergehenden
Verringerung
der
Driftgeschwindigkeit ν zurückzuführen ist.
(Identische Stromstärken mit einer erhöhten
Anzahl von Ladungsträgern implizieren eine
Verringerung der Driftgeschwindigkeit.) Die
Driftgeschwindigkeit ist wiederum über die Abb. 7: Hall-Spannung in Abhängigkeit von der
Temperatur
Lorentzkraft mit der Hall-Spannung verknüpft.
Der Strom im Kristall entsteht gleichermaßen
durch Elektronenstrom und Löcherstrom.
Da die Konzentration von Löchern p und Elektronen n im Eigengeschwindigkeitsbereich ungefähr gleich
ist, tragen letztendlich jene Ladungsträger hauptsächlich zum Hall-Effekt bei, welche die größere
Geschwindigkeit oder
(da ν = μ ・E) die größere Beweglichkeit haben.
Abb. 7 zeigt entsprechend die für p-leitende Materialien typische Vorzeichenumkehr der Hall-Spannung
oberhalb einer bestimmten Temperatur.
www.phywe.com
P2530162
PHYWE Systeme GmbH & Co. KG © All rights reserved
7