Vorbereitungsaufgaben für die dritte Klausur am 20.3.14

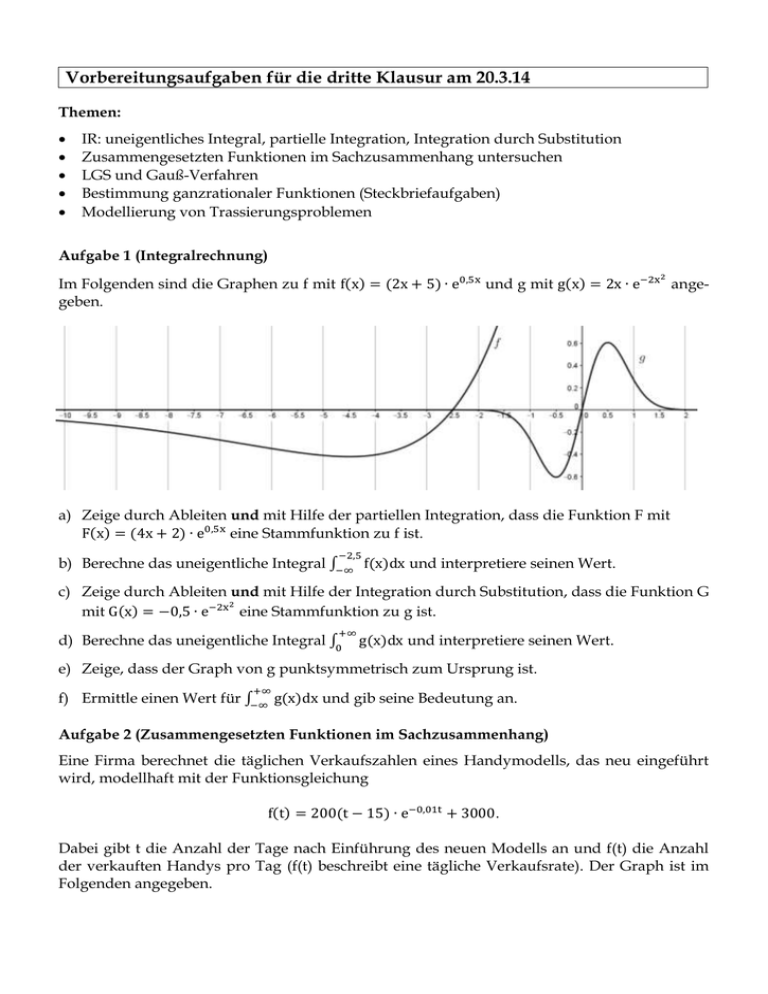
Vorbereitungsaufgaben für die dritte Klausur am 20.3.14
Themen:





IR: uneigentliches Integral, partielle Integration, Integration durch Substitution
Zusammengesetzten Funktionen im Sachzusammenhang untersuchen
LGS und Gauß-Verfahren
Bestimmung ganzrationaler Funktionen (Steckbriefaufgaben)
Modellierung von Trassierungsproblemen
Aufgabe 1 (Integralrechnung)
2
Im Folgenden sind die Graphen zu f mit f(x) = (2x + 5) ∙ e0,5x und g mit g(x) = 2x ∙ e−2x angegeben.
a) Zeige durch Ableiten und mit Hilfe der partiellen Integration, dass die Funktion F mit
F(x) = (4x + 2) ∙ e0,5x eine Stammfunktion zu f ist.
−2,5
b) Berechne das uneigentliche Integral ∫−∞ f(x)dx und interpretiere seinen Wert.
c) Zeige durch Ableiten und mit Hilfe der Integration durch Substitution, dass die Funktion G
2
mit G(x) = −0,5 ∙ e−2x eine Stammfunktion zu g ist.
+∞
d) Berechne das uneigentliche Integral ∫0
g(x)dx und interpretiere seinen Wert.
e) Zeige, dass der Graph von g punktsymmetrisch zum Ursprung ist.
+∞
f) Ermittle einen Wert für ∫−∞ g(x)dx und gib seine Bedeutung an.
Aufgabe 2 (Zusammengesetzten Funktionen im Sachzusammenhang)
Eine Firma berechnet die täglichen Verkaufszahlen eines Handymodells, das neu eingeführt
wird, modellhaft mit der Funktionsgleichung
f(t) = 200(t − 15) ∙ e−0,01t + 3000.
Dabei gibt t die Anzahl der Tage nach Einführung des neuen Modells an und f(t) die Anzahl
der verkauften Handys pro Tag (f(t) beschreibt eine tägliche Verkaufsrate). Der Graph ist im
Folgenden angegeben.
a) Beschreibe den Verlauf des Graphen im Sachzusammenhang.
b) Bestimme f(9) und interpretiere den Wert.
c) Untersuche rechnerisch, wie sich die täglichen Verkaufszahlen langfristig entwickeln.
d) Ermittle den Zeitpunkt, an dem die tägliche Verkaufszahl maximal ist, und berechne die
maximale tägliche Verkaufszahl.
[Hinweis: f´(t) = (230 − 2t) ∙ e−0,01∙t , f´´(t) = (−4,3 + 0,02t) ∙ e−0,01∙t ]
e) Zeige mithilfe von f´(t), dass der Modellfunktion f zufolge die täglichen Verkaufszahlen
ständig sinken, nachdem sie ihr Maximum erreicht haben.
f) Markiere in der obigen Abbildung den einzigen Wendepunkt. Überprüfe dies rechnerisch
und interpretiere die Bedeutung des Wendepunktes.
g) Zeige durch Ableiten und mit Hilfe des Verfahrens der partiellen Integration, dass die
Funktion F mit F(t) = (−20000t − 1700000) ∙ e−0,01∙t + 3000t Stammfunktion von f ist.
115
h) Berechne ∫0 f(t)dt mithilfe des Hauptsatzes der Differential- und Integralrechnung und
gib seine Bedeutung im Sachzusammenhang an.
i) Berechne
1
115−0
115
⋅ ∫0
f(t)dt und interpretiere seinen Wert.
Aufgabe 3 (Lineare Gleichungssysteme und der Gauß-Algorithmus)
Lösen die Gleichungssysteme zu a) und b) systematisch mit dem Gauß-Algorithmus. Führe
mit den TR die Probe durch.
a) I
3x + 6y - 2z = - 4
II 3x + 2y + z = 0
III 1,5x + 5y – 5z = - 9
b)
I
II
III
x+y– z =0
x+
z=2
x - 2y + z = 2
c) Bestimme alle ganzrationalen Funktionen vom
Grad 2, deren Graphen
durch A(0/2) und B(6/8)
verlaufen.
Aufgabe 4 (Steckbriefaufgaben)
Formuliere die Bedingungen und das Gleichungssystem. Lösen dann das GLS mit dem TR
und gib die gesuchte Funktionsgleichung an.
a) Der Graph einer ganzrationalen Funktion 4. Grades ist zur y-Achse symmetrisch und hat in
W(1/3) einen Wendepunkt. Die Steigung an der Stelle x = 1 hat den Wert –2.
b) Der Graph einer ganzrationalen Funktion f vom Grad 3 ist punktsymmetrisch zum Ursprung, verläuft durch A(1/2) und hat für x = 1 eine waagerechte Tangente.
Aufgabe 5 Modellierung eines Straßenverlaufs
Die Abbildung zeigt zwei geradlinig verlaufende Straßenstücke AC und BD. Es soll nun eine
Kurve gefunden werden, welche die Straßenstücke miteinander verbindet. Die Übergänge von
A und B sollen sprungfrei und knickfrei sein.

Bestimme Gleichungen der Geraden durch die Punkte A und C bzw. B und D.

Erkläre, was ein sprung- und knickfreier Übergang anschaulich bedeutet.

Ermittle eine Funktion dritten Grades, welche die vorgegebene Situation modelliert.

Untersuche, unter welcher Bedingung, das Kurvenstück durch eine Parabel modelliert
werden könnte.

Zeige, dass f in beiden Übergängen nicht krümmungssprungfrei ist und begründe, welchen
Grad eine Funktionen haben müsste, damit die Übergänge krümmungssprungfrei sind.
Vorbereitungsaufgaben für die dritte Klausur am 20.3.14 - Lösungen
Aufgabe 1 (Integralrechnung)
f(x) = (2x + 5) ∙ e0,5x und g mit g(x) = 2x ∙ e−2x
2
a)
 F´(x) = 4 ∙ e0,5x + (4x + 2) ∙ 0,5 ∙ e0,5x = (4 + 2x + 1) ∙ e0,5x = f(x)
 ∫(2x + 5) ∙ e0,5x dx =
⏟ (2x + 5) ∙ 2e0,5x − ∫ 2 ∙ 2e0,5x dx = (4x + 10) ∙ e0,5x − 8e0,5x = F(x)
u=2x+5
u´=2
v´=e0,5x
v=2e0,5x
b)
−2,5
 ∫L f(x)dx = F(−2,5) − F(L) = −8 ∙ e−1,25 − (4L + 2)e0,5L →

−8 ∙ e−1,25 = ∫−∞ f(x)dx
Der Wert des Integrals beschreibt den negativen Flächeninhalt der unbeschränkten Fläche,
den der Graph von f über dem Intervall [-; -2,5] mit der x-Achse einschließt.
c)
2
2
 G´(x) = −0,5 ∙ e−2x ∙ (−4x) = 2x ∙ e−2x = g(x)
2
 ∫ 2x ∙ e−2x dx
=
⏟
∫ −0,5ez dz = −0,5ez + c
z=−2x2
z´=−4x
dz=−4x dx
−0,5 dz=2x dx
=
⏟
2
− 0,5e−2x + c
z=−2x2
d)
2
R
 ∫0 g(x)dx = G(R) − G(0) = −0,5e−2R − (−0,5) →

−2,5
L→−∞
R→+∞
+∞
0,5 = ∫0
g(x)dx
Der Wert des Integrals beschreibt den Flächeninhalt der unbeschränkten Fläche, den der
Graph von g mit der positiven x-Achse einschließt.
e)
2
2
 g(−x) = 2(−x) ∙ e−2(−x) = −2x ∙ e−2x = −g(x)
f)
2
2
R
+∞
 ∫L g(x)dx = G(R) − G(L) = −0,5e−2R − (−0,5e−2L ) →
0
=
g(x)dx
∫
−∞
R→+∞
L→−∞

+∞
Alternativ: Wegen der Punktsymmetrie des Graphen von g gilt: ∫0
+∞
also: 0 = ∫0
0
+∞
g(x)dx + ∫−∞ g(x)dx = ∫−∞ g(x)dx.
0
g(x)dx = − ∫−∞ g(x)dx,

Bedeutung: Das Integral beschreibt die Flächenbilanz der unbegrenzten Fläche, die der
Graph von g mit der gesamten x-Achse einschließt.
Aufgabe 2 (Zusammengesetzten Funktionen im Sachzusammenhang)
f(t) = 200(t − 15) ∙ e−0,01t + 3000
a)
 Graph stellt die Verkaufsrate in Handys pro Tag dar.
 Zu Beginn: Verkaufsrate ist mit 0 global am kleinsten.
 Nach ca. 125 Tagen ist die Zahl der täglich verkauften Handys mit ca. 9300 Handys pro Tag
global am größten.
 Die Verkaufsrate nimmt zu Beginn global am schnellsten zu und nach ca. 250 Tagen lokal
am schnellsten ab.
 Langfristig werden 3000 Handys pro Tag verkauft.
b)
 f(9) = 200 ∙ (9 − 15) ∙ e−0,01∙t + 3000 ≈ 1903 Handys pro Tag
 f(9) beschreibt die Verkaufsrate am 9 Tag in Handys pro Tag
c)
 f(t) = 200 ∙ (t − 15) ∙ e−0,01∙t + 3000 →

𝑡⟶+∞
3000
Denn: 200 ∙ (t − 15) ∙ e−0,01∙t strebt gegen Null für große Werte für t, da der e-Term (er
strebt gegen Null) das Verhalten dominiert.
d)
 f´(t) = (230 − 2t) ∙ e−0,01∙t (Produkt-, Ketten-, Summenregel)
 f´(t) = (230 − 2t) ∙ e−0,01∙t = 0 ⟺ 230 − 2t = 0 ⇔ t = 115
 f´´(115) =< 0, f(115) ≈ 9333: Nach 115 Tagen wird eine maximale Verkaufsrate von 9233
Handys pro Tag erreicht.
e)
 f´(t) = (230 − 2t) ∙ e−0,01∙t < 0 für t > 115, da 230 − 2t < 0 und e−0,01∙t > 0. Daher fällt der
Graph von f für t > 115.
f)




Einzeichnen des WP (siehe oben)
f´´(t) = (−4,3 + 0,02t) ∙ e−0,01∙t = 0 ⟺ −4,3 + 0,02t = 0 ⇔ t = 215
f´´´(215) > 0 und f(215) ≈ 7659: W(215/7659) ist lokaler WP.
WP beschreibt den Zeitpunkt, an dem die Verkaufsrate am stärksten abnimmt.
g)
 F´(t) = −20000 ∙ e−0,01∙t + (−20000t − 1700000) ∙ (−0,01) ∙ e−0,01∙t + 3000
= (−20000 + 200t + 17000) ∙ e−0,01∙t + 3000 = (200t − 3000) ∙ e−0,01∙t + 3000
= 200(t − 15) ∙ e−0,01∙t + 3000 = f(t)
 ∫ 200(t − 15) ∙ e−0,01t dt
=
⏟
− 20000 (𝑡 − 15) ∙ e−0,01t − ∫ −20000e−0,01t dt
u=200(t−15)
u´=200
v´=e−0,01t
v=−100e−0,01t
= (−20000t + 300000) ∙ e−0,01t − 2000000 ∙ e−0,01t = (−20000t − 1700000) ∙ e−0,01t
h)
115
 ∫0 f(t)dt = F(115) − F(0) = (−20000 ∙ 115 − 1700000) ∙ e−1,15 + 1700000 ≈ 433453
 Bedeutung: Anzahl der verkauften Handys in den ersten 115 Tagen.
i)


1
115−0
115
⋅ ∫0
f(t)dt ≈ 3769 Handys pro Tag
Der Wert beschreibt die durchschnittliche tägliche Verkaufsrate der ersten 115 Tage.
Aufgabe 3 (Lineare Gleichungssysteme und der Gauß-Algorithmus)
a)
 Lösung: x = -1, y = 0,5 z = 2 (vgl. AB1)
b)
 Lösung: x= 1, y = 0, z = 1
c)
 f(x) = ax 2 + bx + c
 f(0) = 2: c = 2 und (II) f(6) = 8: 36a + 6b + c = 8  6a + b = 1  b = 1 – 6a
 Das LGS bzw. die Steckbriefaufgabe ist unterbestimmt. Man erhält die Schar von Funktionen: f(x) = ax 2 + (1 − 6a)x + 2 für eine beliebige Zahl a  0.
Aufgabe 4 (Steckbriefaufgaben)
a)




f(x) = ax 4 + bx 2 + c (Funktion ist wegen der Achsensymmetrie des Graphen gerade)
f´(x) = 4ax 3 + 2bx, f´´(x) = 12ax 2 + 2b,
f(1) = 3: a + b + c = 3, (II) f´´(1) = 0: 12a + 2b = 0 (III) f´(1)= -2: 4a + 2b = -2  2a + b = -1.
Man erhält das LGS:
1 1 1
3
12 2 0 | 0. Mit dem TR erhält man die Lösung: a = 0,25, b = -1,5 und c = 4,25.
2 1 0 −1
b)




f(x) = ax 3 + bx (Funktion ist wegen der Punktsymmetrie des Graphen ungerade)
f´(x) = 3ax 2 + b,
(I) f(1) = 2: a + b = 2, (II) f´(1) = 0: 3a + b = 0.
(II) – (I) ergibt 2a = -2 bzw. a = -1 und damit b = 3.
Aufgabe 5 Modellierung eines Straßenverlaufs
a)
 g(x) = gAC(x) = 5x
 h(x) = gBD(x) = -2x +12
b)
 Ein sprungfreier Übergang bedeutet, dass eine
Straße ohne Lücke in die andere Straße übergeht.
 Ein knickfreier Übergang bedeutet, dass die beiden
Straßen im Übergangspunkt die gleiche Steigung
haben.
c)
 f(x) = ax 3 + bx 2 + cx + d, f´(x) = 3ax 2 + 2bx + c
 Bedingungen aufstellen:
(I) f(0) = g(0) = 0, (II) f´(0) = g´(0) = 5
(III) f(4) = h(4) = 4, (IV) f´(4) = h´(4) = -2
 Aus (I) folgt d = 0 und aus (II) unmittelbar c = 5. (III) und (IV) ergeben folgendes LGS:
(III) 64a + 16b + 4c + d = 4 und (IV) 48a + 8b + c = -2. Setzt man c und d ein, ergibt sich:
 (III) 64a + 16b = -16 und (IV) 48a + 8b = -7. Mit dem TR erhält man: a = 0,0625 und b = -1,25
 f(x) = 0,0625x 3 − 1,25x 2 + 5x und f´(x) = 0,1875x 2 − 2,5x + 5
d)
 Es müsste eine Parabel mit einer Funktionsgleichung der Form p(x) = ax 2 + 5x sein, da der
Punkt A als Koordinatenursprung ein knick- und sprungfreier Übergang ist. Mit f(4) = 4
ergibt sich 16a + 20 = 4 oder a = -1. Damit gilt für die Funktionsgleichungen von p und p´
p(x) = −x 2 + 5x und p´(x) = −2x + 5. Wegen p´(4) = −2 ∙ 4 + 5 = −3 ist der Übergang
nicht knickfrei. Eine Parabel hat in der obigen Situation mindestens einen Übergang der
nicht knickfrei ist.
e)
 f´´(x) = 0,375x − 2,5
 f´´(0) = −2,5 ≠ g´´(0) = 0 und f´´(4) = -1 ≠ h´´(0) = 0
 Ein Graph mit krümmungssprungfreien Übergängen A und B kann durch eine GRF vom
Grad fünf modelliert werden (es kommen zwei Bedingungen dazu).
 Wenn es einen Graphen einer GRF vierten Grades gäbe, für den an den knick- und
sprungfreien Übergangsstellen die zweite Ableitung den Wert Null annimmt, könnte das
Problem auch durch eine Funktion vierten Grades beschrieben werden (denn dann würde
f´´(0) = g´´(0) = 0 und f´´(4) = h´´(4) = 0 gelten).