121 200607 LK Math Ue7 - Helmholtz

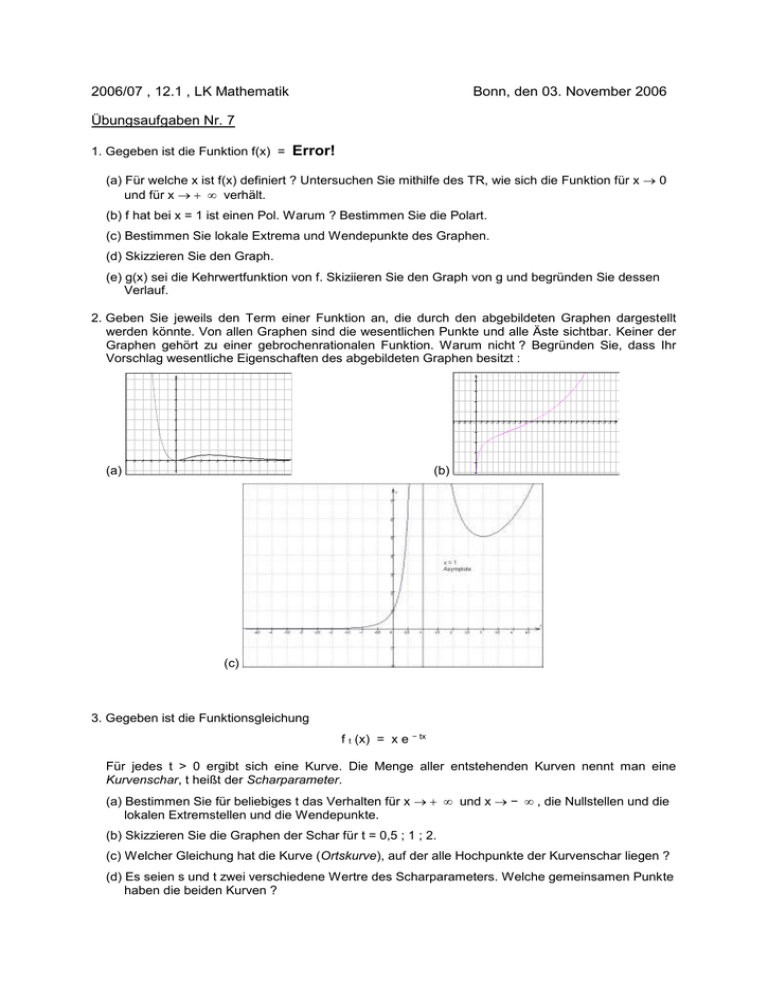
2006/07 , 12.1 , LK Mathematik
Bonn, den 03. November 2006
Übungsaufgaben Nr. 7
Error!
1. Gegeben ist die Funktion f(x) =
(a) Für welche x ist f(x) definiert ? Untersuchen Sie mithilfe des TR, wie sich die Funktion für x  0
und für x  verhält.
(b) f hat bei x = 1 ist einen Pol. Warum ? Bestimmen Sie die Polart.
(c) Bestimmen Sie lokale Extrema und Wendepunkte des Graphen.
(d) Skizzieren Sie den Graph.
(e) g(x) sei die Kehrwertfunktion von f. Skiziieren Sie den Graph von g und begründen Sie dessen
Verlauf.
2. Geben Sie jeweils den Term einer Funktion an, die durch den abgebildeten Graphen dargestellt
werden könnte. Von allen Graphen sind die wesentlichen Punkte und alle Äste sichtbar. Keiner der
Graphen gehört zu einer gebrochenrationalen Funktion. Warum nicht ? Begründen Sie, dass Ihr
Vorschlag wesentliche Eigenschaften des abgebildeten Graphen besitzt :
y
y
8
4
7
3
6
2
5
1
x
4
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2
2.1
2.2
2.3
2.4
2.5
3
-1
2
-2
1
-3
x
-3
(a)
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
-4
(b)
-1
-5
(c)
3. Gegeben ist die Funktionsgleichung
f t (x) = x e − tx
Für jedes t > 0 ergibt sich eine Kurve. Die Menge aller entstehenden Kurven nennt man eine
Kurvenschar, t heißt der Scharparameter.
(a) Bestimmen Sie für beliebiges t das Verhalten für x  und x − , die Nullstellen und die
lokalen Extremstellen und die Wendepunkte.
(b) Skizzieren Sie die Graphen der Schar für t = 0,5 ; 1 ; 2.
(c) Welcher Gleichung hat die Kurve (Ortskurve), auf der alle Hochpunkte der Kurvenschar liegen ?
(d) Es seien s und t zwei verschiedene Wertre des Scharparameters. Welche gemeinsamen Punkte
haben die beiden Kurven ?