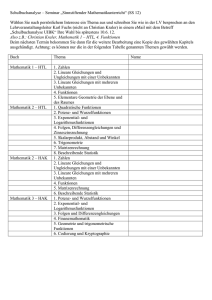
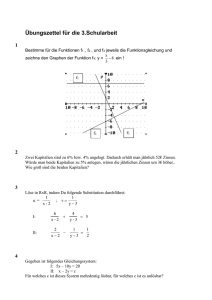
II: x

Mathematik
4. Klasse AHS
Foto: linkset.de
Zusammenfassung des Stoffs
Mattias Fabian
Für den Inhalt wird keine Haftung übernommen. © 2010
Wurzeln & Pythagoras
a = √𝑥
 Radikant
Es gilt außerdem: √45 = √9 . 5 = √9 . √5 = 3 . √5
RATIONALE ZAHLEN
Können als Bruch angeschrieben werden
IRRATIONALE ZAHLEN
können nicht als Bruch…
N … Menge der NATÜRLICHEN ZAHLEN {0, 1, 2, 3 …}
Z … Menge der GANZEN ZAHLEN {…, -3, -2, -1, 0, 1, 2, 3 …}
Q … Menge der RATIONALEN ZAHLEN (Bruchzahlen)
R … Menge der REELEN ZAHLEN (rationale und irrationale Zahlen)
Steigungsdreieck:
Steigung =
h
𝑤
=
p
100
h
.
w
Die Hypotenuse c eines rechtwinkeligen Dreiecks wird durch die Höhe in zwei
Abschnitte p und q geteilt. Diese werden als HYPOTENUSENABSCHNITTE
C
bezeichnet.
b
KATHETENSÄTZE: a² = c . p
b² = c . q
HÖHENSATZ:
h² = p . q
a
h
∝
𝛽
A
B
q
F
p
c
Funktionen
Einem Wert einer Größe wird ein Wert einer andren Größe zugeordnet. Die
Kurve in einem Diagramm wird als GRAPH bezeichnet. Es gibt
 Homogene lineare Funktionen
 Inhomogene lineare Funktionen
 Nichtlineare Funktionen
Homogene lineare Funktion: Der Graph ist eine Gerade (linear), die
Funktionsgleichung hat die Form: y = k . x
Der Graph geht (homogen) durch den Koordinatenursprung.
Inhomogene lineare Funktion: Der Graph ist eine Gerade und geht nicht durch
den Koordinatenursprung 0. Die Funktionsgleichung hat die Form: y = k . x + d
wobei d ≠ 0. D ist eine konstante reelle Zahl (ungleich Null) und wird als
Achsenabschnitt bezeichnet.
Nichtlineare Funktion: Der Graph ist keine Gerade, die Funktionsgleichung hat
die Form: y = k . x + d (wobei k und d beliebige reelle Zahlen sind).
Funktionen mit der Gleichung y = a . x² nennt man Quadratfunktionen.
Der Graph wird als Parabel bezeichnet.
𝒌
Funktionen mit der Gleichung der Form y = , wobei k eine konstante reelle
𝒙
Zahl (außer Null) ist, beschreiben indirekt proportionale Zusammenhänge.
Der Graph wird als Hyperbel bezeichnet.
Lineare Gleichungen mit zwei Unbekannten
Eine Gleichung mit zwei Unbekannten hat die Form: a . x + b . y = c (a, b ≠ 0)
Die Lösung einer solchen Gleichung besteht aus zwei Zahlen – einer Zahl für x
und einer dazu gehörenden Zahl y –
also aus einem geordneten Zahlenpaar (x|y)
Eine Gleichung mit zwei Unbekannten kann beliebig viele solcher Zahlenpaare,
die die Gleichung erfüllen, als Lösungen haben. Man kann die Zahlenpaare auch
als Punkte in einem Koordinatensystem darstellen. Diese Punkte liegen auf
einer Geraden, weil man die Gleichung auf die Form y = k . x + d, die Gleichung
einer linearen Funktion, bringen kann.
z.B: 2x – y = 1
Wählt man für x eine beliebige Zahl, lässt sich y berechnen (und umgekehrt):
x=0y=-1
x=2y=3
z.B: Es gibt Abteile mit 3 und 4 Liegeplätzen. 36 Personen benötigen einen
Platz. Wie viele Abteile werden benötigt (Vollbesetzung)?
x … Anzahl der Dreierabteile, y … Anzahl der Viererabteile
Gleichung: 3x + 4y = 36
Lösungen: (12|0), (8|3), (4|6), (0|9)
Um ein Gleichungssystem zu lösen gibt es zwei Möglichkeiten:
a) Grafische Lösung
b) Rechnerische Lösung
Grafische Lösung:
Zwei lineare Gleichungen mit zwei Unbekannten bilden ein LINEARES
GLEICHUNGSSYTEM. Die Lösung eines solchen Gleichungssystems besteht aus
einem geordneten Zahlenpaar (x|y), das beide Gleichungen erfüllt.
In der Zeichnung erhält man dieses Zahlenpaar als Schnittpunkt (S) der
Graphen.
z.B:
I: y = -x + 2
Sonderfälle: die Geraden sind parallel (keine Lösung)
II: y = x
die Geraden fallen zusammen (∞ Lösungen)
S (1|1), daher x = 1, y = 1
Rechnerische Lösung:
Zum Ermitteln der Lösung gibt es einige rechnerisches Verfahren, die zu einer
(linearen) Gleichung mit zwei Unbekannten führen. Mit Hilfe des Einsetzens
des Ergebnisses dieser Gleichung kann die zweite Unbekannte gefunden
werden. Die Lösung erfüllt beide Gleichungen, daher müssen bei der Probe
beide Gleichungen überprüft werden.
1) Gleichsetzungsverfahren
Beide Gleichungen werden nach derselben Variablen aufgelöst und die
enthaltenen Terme gleichgesetzt.
z.B: I: x + 2y = 7
II: x – 3y = 1
I: x = 7 – 2y
Gleichsetzten: 7 – 2y = 1 + 3y
𝟔
II: x = 1 + 3y
y=
𝟓
6
𝟐𝟑
5
𝟓
II: x = 1 + 3 . =
2) Einsetzungsverfahren
Aus einer der beiden Gleichungen wird eine Variable ausgedrückt. Der
enthaltene Term wird in die andere Gleichung eingesetzt.
z.B: I: x + 2y = 7
II: x – 3y = 1
Einsetzten für x: II: (7 – 2y) – 3y = 1
𝟔
I: x = 7 – 2y
y=
𝟓
6
𝟐𝟑
5
𝟓
I: x = 7 - 2 . =
3) Additionsverfahren
Die beiden Gleichungen werden so umgeformt, dass bei einer
Unbekannten die Gegenzahlen als Koeffizienten auftreten. Danach
werden die Gleichungen addiert.
z.B: I: x + 2y = 7 |. (-1)
II: x – 3y = 1
6
I: -x – 2y = -7
I: x + 2 . = 7
II: x – 3y = 1
-5y = -6
𝟔
y=
x=
𝟐𝟑
5
𝟓
𝟓
Kreis
Flächeninhalt: A = r² . 𝝅
| Kreisumfang: u = 2r . 𝝅
r
Länge Kreisbogen: b =
𝐫 . 𝛑 .𝛂
𝟏𝟖𝟎
Flächeninhalt Sektor: A =
(𝛼 in Grad)
M
𝐫² . 𝛑 .𝛂
𝟑𝟔𝟎
=
𝛼
b
b. r
2
r
Binomische Lehrsätze:
(a + b) . (a – b) = a² - b²
(a + b)²
= a² + 2ab + b²
(a – b)²
= a² - 2ab + b²
(a + b)³
= a³ + 3a²b + 3ab² + b³
(a – b)³
= a³ - 3a²b + 3ab² - b³
Binomischer Lehrsatz:
𝑛
𝑛
(𝑥 + 𝑎) = ∑ ( ) 𝑥 𝑘 𝑎𝑛−𝑘
𝑘
𝑛
𝑘=0
Pythagoräischer Lehrsatz
A² + b² = c² (wenn: a, b  Katheten, c  Hypotenuse)
Oberflächen & Rauminhalte
Quadratische Pyramide:
O = M + G = a² + 4 . Dreieck
1
V = . G. h
3
Kegel:
O = G + M = r²𝜋 +
r² . π .α
1
360
V = . G. h
3
Gleichschenkeliges Dreieck:
a .ha
A=
2
Gleichseitiges Dreieck:
h=
𝑎 .√3
2
| A=
𝑎² .√3
4