x(t)

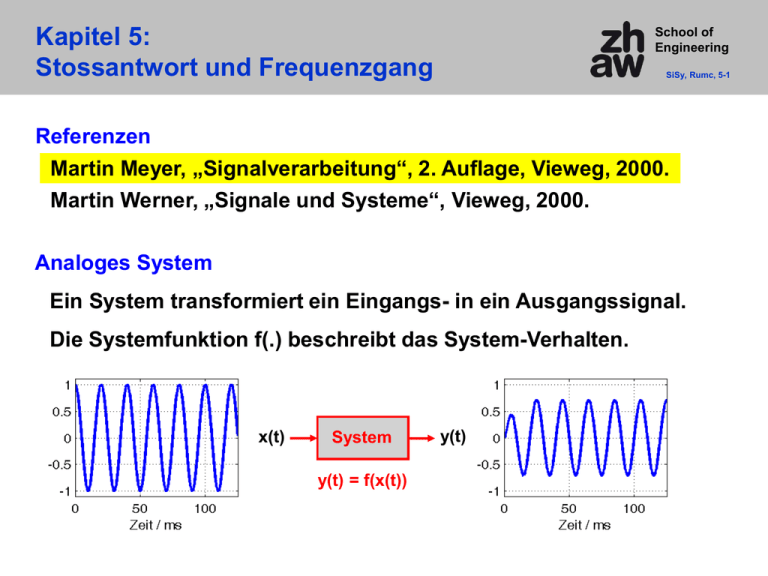
Kapitel 5:
Stossantwort und Frequenzgang
School of
Engineering
SiSy, Rumc, 5-1
Referenzen
Martin Meyer, „Signalverarbeitung“, 2. Auflage, Vieweg, 2000.
Martin Werner, „Signale und Systeme“, Vieweg, 2000.
Analoges System
Ein System transformiert ein Eingangs- in ein Ausgangssignal.
Die Systemfunktion f(.) beschreibt das System-Verhalten.
x(t)
System
y(t) = f(x(t))
y(t)
School of
Engineering
System-Klassifizierung
SiSy, Rumc, 5-2
Linearität / Superpositionsprinzip
x(t) = k1·x1(t) + k2·x2(t) => y(t) = k1·f(x1(t)) + k2·f(x2(t)) = k1·y1(t) + k2·y2(t)
Linearkombination von
Eingangssignalen
Linearkombination von
zugehörigen Ausgangssignalen
t
Beispiel 1:
t
y(t)   (x 1 (u)  x 2 (u))  du 

Beispiel 2:
x(t)
y(t) 
lineares
System
x(t)
 x(u)  du

t
t
 x (u) du   x
1

nicht-lineares
System
2
(u) du = y1(t) + y2(t)

y(t)  x 2 (t)
y(t)  x 1 (t)  x 2 (t)   x 12 (t)  x 22 (t)  2  x 1 (t)  x 2 (t)
2
„Kunstgriff“ Linearisierung im Arbeitspunkt
(Beispiel: Kleinsignal-Ersatzschaltbild)
neue Frequenzen !
≠ y1(t) + y2(t)
School of
Engineering
System-Klassifizierung
SiSy, Rumc, 5-3
Zeitinvarianz
Systemeigenschaften ändern sich zeitlich nicht
x(t)
x(t-t0)
lineares
System
x(t) = ε(t)
y(t)
y(t-t0)
y(t)
x(t-t0) = ε(t-t0)
t
t0
LTI-Systeme
linear, time-invariant systems
wichtige Unterklasse der linearen Systeme
wir fokussieren uns auf LTI-Systeme und lernen
mächtiges mathematisches Instrumentarium kennen
y(t-t0)
t
t0
School of
Engineering
System-Klassifizierung
SiSy, Rumc, 5-4
Kausalität
Ein kausales System reagiert erst dann mit einem
Ausgangssignal, wenn ein Eingangssignal anliegt.
Die Stossantwort von kausalen Systemen verschwindet für t<0.
δ(t)
h(t)
kausales
System
t
t
Technisch realisierbare Systeme sind kausal !
Stabilität
zweckmässige Definition: Bounded Input => Bounded Output
Ix(t)I ≤ A < ∞ => Iy(t)I ≤ B < ∞ für A und B > 0
School of
Engineering
Stoss- bzw. Impulsantwort
SiSy, Rumc, 5-5
Definition Stoss- bzw. Impulsantwort h(t)
x(t) = δ(t)
y(t) = h(t)
LTISystem
t
t
System-Antwort auf Anregung mit allen Frequenzkomponenten
Die Stossantwort h(t) beschreibt ein LTI-System vollständig
Ausgangssignal = Faltung von Eingangssignal mit der Stossantwort
Beweis siehe nächste Folie
x(t)
LTISystem
t
y(t) = x(t) * h(t)
School of
Engineering
Herleitung der Faltung
SiSy, Rumc, 5-6
x(t)
LTISystem
y(t) = x(t) * h(t)
= h(t) * x(t)
t
Faltungsintegral

x(t) = Superposition von ∞-vielen,
zeitverschobenen und gewichteten
Dirac-Stössen
y(t) 
 x( )  h(t  τ) dτ

x(0)·h(t)
LTISystem
x(0)·δ(t)
t
x(t0)·h(t-t0)
x(t0)·δ(t-t0)
t0
t
Definition
t
LTISystem
Zeitinvarianz
t0
t
School of
Engineering
Beispiel 1: Faltung
SiSy, Rumc, 5-7
Schrittantwort eines RC-Tiefpass-Filters 1. Ordnung
x(t)
y(t) = x(t) * h(t)
t
1
LTISystem
y(t0)
1
t0
t0
„Stossantwort“
„Faltung“
y(t 0 )   x( )  h(t 0  τ) dτ
0
x(τ)·h(t0-τ)
h(t)
x(τ)
1
t
t0
t
τ
1. Verschiebung von h(τ) um t0 => h(τ-t0)
2. Zeitumkehr bzw. Faltung => h(-(τ-t0)) = h(t0-τ)
3. Integration des Produkts x(τ)·h(t0-τ) => y(t0) = gelbe Fläche
School of
Engineering
Beispiel 2: Faltung
SiSy, Rumc, 5-8
Stossantwort eines stabilen Systems
BIBO-stabiles System
Ix(t)I ≤ A < ∞ => Iy(t)I ≤ B < ∞ für A und B > 0
Bestimmung des Ausgangssignals mit der Faltung
y(t) 






 x(τ)  h(t  τ) dτ   x(τ)  h(t  τ) dτ  A   h(τ) dτ  B  
Die Stossantwort eines stabilen Systems ist absolut integrierbar.

 h(τ) dτ  

Frequenzgang H(f) und Übertragungsfunktion H(s) existieren.
School of
Engineering
Frequenzgang
SiSy, Rumc, 5-9
Faltungstheorem der Fouriertransformation
x(t)*h(t) ○-● X(f)·H(f)

Zeitbereich
x(t)
LTISystem
Stossantwort
h(t)
y(t) 
 x( )  h(t  τ) dτ

y(t) = x(t) * h(t)
○-●
Frequenzgang
H(f)
Frequenzbereich
X(f)
Y(f) = X(f) · H(f)
h(t) und H(f) bzw. H(s) sind ein Fourier- bzw. Laplace-Paar.
h(t): Stossantwort, H(f): Frequenzgang, H(s): Übertragungsfunktion
School of
Engineering
Frequenzgang
SiSy, Rumc, 5-10
Amplitudengang
IY(f)I = IX(f)I · IH(f)I
Phasengang
φY(f) = φX(f) + φH(f)
f0-Komponente X(f0) des Eingangssignals x(t)
LTI-System multipliziert Amplitude IH(f0)I
LTI-System dreht Phase um φH(f0)
Ein LTI-System generiert keine neuen Frequenzen
die nicht schon im Eingangssignal vorhanden sind
im Gegensatz zu einem nicht-linearen System (neue Frequenzen!)
cos(2π·f0·t)
LTISystem
IH(f0)I·cos(2π·f0·t + φ(f0))
School of
Engineering
Frequenzgang
SiSy, Rumc, 5-11
Beispiel RC-Tiefpass-Filter 1. Ordnung
Amplitudengang IH(f)I
τ = RC = 10-3 / (2π)
C
x(t)
y(t)
dB
R
-3dB
Stossantwort
1
h(t)  u(t)   e  t/τ

Phasengang φH(f)
- 6°
Frequenzgang
H(f) 
1
1  j  2π  f  τ
- 45°
- 6 dB / Oktave
- 20 dB / Dekade
School of
Engineering
Schrittantwort
SiSy, Rumc, 5-12
Stossantwort
δ(t)
h(t)
LTISystem
t
t
Schrittantwort
ε(t)
y(t)
1
LTISystem
1
t
t
t
t
ε(t) 
 δ(τ) dτ

E(s) = 1/s
y(t) 
 h(τ)  dτ
bzw. h(t) = dy(t) / dt

Y(s) = (1/s)·H(s)