E1-12Fo1 - Bionik TU
Werbung

Ingo Rechenberg
PowerPoint-Folien zur 1. Vorlesung „Evolutionsstrategie I“
Von der „Insel der Krebse“ zum ES-Kalkül
Geschichte, Gegenwart und Zukunft der Evolutionsstrategie
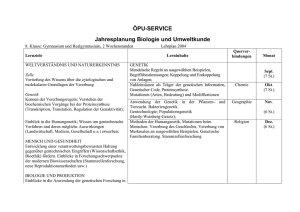
Biologische Evolution
in Kurzform
1
Schleimklumpen in der
Ursuppe der Erde
2
Im Urozean entwickeln
sich die Fische
3
Vorsichtig erobert
das Leben das Land
4
Unsere Vorfahren
erklettern die Bäume
5
Die Krönung der
Evolution denkt über
seine Entstehung nach
Evolutionsstreit
und worum es dabei geht
Die Annahme, dass das Auge mit all seinen
unnachahmlichen Einrichtungen, die Linse den
verschiedenen Entfernungen anzupassen,
wechselnde Lichtmengen zuzulassen und
sphärische wie chromatische Abweichungen zu
verbessern, durch die natürliche Zuchtwahl
entstanden sei, erscheint, wie ich offen bekenne,
in höchstem Grade absurd.
Aus Charles Darwin: „Die Entstehung der Arten“
Evolution einer Augenlinse
Computersimulation der Evolution
einer Sammellinse
Verformbarer Glaskörper
dk
F
qk
qk2 Minimum
Von den Anfängen
der Evolutionsstrategie
Wissenschaftler als Autoren von Science-Fiction
Johannes Alfven
Isaac Asimov
Wernher von Braun
Konrad Fialkowski
Stanislav Lem
Konstantin Ziolkowski
Fred Hoyle
Carl Sagan
Michael Crichton
Frank Schätzing
Bob Shaw
Andere Tage, andere Augen
Text
d = 20 mm
= 10 8 Atomlagen
C
C
10 Bilder/s Austritt nach 115 Tagen
Speicherzeit = 1/10 s pro Atomschicht
Science-Fiction:
Langsamglas (Retardit)
Meldung vom 19. 3. 2005
Ausgebremstes Licht
Siliziumchip verlangsamt Lichtpulse
um ein Hundertfaches
Wissenschaftler der Stanford-Universität in Kalifornien
haben einen photonischen Kristall hergestellt, der die
Ausbreitungsgeschwindigkeit von Lichtpulsen um den Faktor
Hundert herabsetzen kann.
Meldung vom 9. 9. 2010
Lichverzögerung im Chip
In einer gasgefüllten hohlen Glasfaser wurde Infrarotlicht
auf ein 1200-stel der Lichtgeschwindigkeit abgebremst.
Anatolij Dnjeprow
Anatolij Dnjeprow
Insel der Krebse:
Eine Science-Fiction-Erzählung über
künstliche Evolution. Die Geschichte
ist Ausgangspunkt für die Entwicklung
der Evolutionsstrategie 1964.
http://www.bionik.tu-berlin.de/institut/skript/inskreb.htm
Der Versuch von
Ingenieur Cookling
Selbstreproduktion
mit Fehlern
Exponentielle
Vermehrung
Kampf ums
Dasein
Evolution á la
DARWIN
U. Berg
Insel der Krebse
Experiment „künstliche Evolution“
Gesucht ist ein einfaches technisches System mit den Eigenschaften:
1. Das System soll manuell mit geringstem Aufwand bei
vorgegebener Fehlerhäufigkeit reproduziert werden können.
2. Das System soll eine Qualität (Tauglichkeit) besitzen,
die besonders einfach gemessen werden kann.
Insel
Windkanal
Stahlhautprofil
Krebs
Verstellbarkeit anstelle
der Selbstreproduktion
Zufällige
Verstellung
anstelle der fehlerhaften
Selbstreproduktion
Idee für ein mechanisches Evolutionsexperiment
„Darwin“ im Windkanal
Schlüsselexperiment mit der Evolutionsstrategie
1964
Text
Zahl der Einstellmöglichkeiten:
515 = 345 025 251
Analogien
- Evolutionsstrategie
Biologie
Technik
Erbanlagen, niedergeschrieben
im DNA-Molekül (Genotyp)
Winkelgrade, notiert auf
einem Protokollblatt
Sichtbares Erscheinungsbild
eines Lebewesens (Phänotyp)
Eingestellte Form der
Gelenkplatte im Windkanal
Zunehmende Tauglichkeit des
Lebewesens in der Umwelt
Abnehmender Widerstand der
Gelenkplatte im Windkanal
xi
2 3
1
4
5
x1
x2
x3
x5
x4
Senkrecht aus der
Wand ragende Nägel
5 4 3 2 1 0
+1 + 2 +3 + 4 + 5
Fiktive Mutationsmaschine
GALTONsches Nagelbrett
W id e rs ta n d
6
E rg e b n is
4
2
0
0
40
80
120
160
200
240
280
M u ta tio n e n
320
Künstliche Evolution: Gelenkplatte im Windkanal
Ändern
der
Umwelt
W id e rs ta n d
6
5
E rg e b n is
4
3
2
1
0
20
40
60
80
100
120
140 160 180
M u ta tio n e n
200
Künstliche Evolution: Gelenkplatte im Windkanal
18. November 1964
Evolution eines
90° Rohrbogens
1965
6 Hand bewegte Stangen mutieren
einen Rohrkrümmer
Start
Ergebnis
Text
Evolution eines
180° Rohrbogens
1980
10 Roboter betätigte Seilzüge mutieren
einen Rohrbogen
Start
Ergebnis
10% verminderte Strömungsverluste gegenüber der Kreisform
Start
Ergebnis
Optimaler 90°-Strömungskrümmer
Start
Ergebnis
Optimaler 180°-Strömungskrümmer
Heißwasserdampfdüse für das
Evolutionsexperiment mutierbar gemacht
Text
0
1
16
31
2
17
32
3
18
33
4
19
34
5
20
35
6
21
36
7
22
37
8
23
38
9
24
39
10
25
40
11
26
41
12
27
42
13
28
43
14
29
44
15
30
45
SCHWEFELs
Evolutionsexperiment
mit einer
Heißwasserdampfdüse
Evolution des Pferdefußes
Vom Eohippus zum Equus (60 Millionen Jahre)
Pinebrook, US Navy
Evolution eines Rotationskörpers minimalen Widerstands
(Querschnitt und Länge des Rotationskörpers fest)
Rabengeier mit
aufgespreizten Flügelenden
Nachkommen
realisieren
ca- cw- Messung
Flexible
Bleistreifen
Neue
Generation
Eltern
eingeben
Nachkommen
bewerten
Künstliche Evolution im Windkanal
cw2
ca3
Text
Generation
0
3
6
9
15
12
18
21
24
Evolution eines
Spreizflügels im Windkanal
27
Diplomarbeit: Michael Stache
Auftriebsbeiwert ca
1,2
Spreizflügel
versus
Normalflügel
0,8
cw2
= 0,0216
c3
a min
0,4
0
Streckung =3,8
0
0,1
0,2
0,3
Widerstandsbeiwert cw
cw2
= 0,0188
c3
a min
Was gewinnt der Vogel
durch aufgespreizte Flügelenden ?
1000 m
a
Zeit: ?
b
Zeit: ?
EvolutionsWettkampf
Text
Daten für Bussard
Formel für die Sinkgeschwindigkeit
vsink
2 g G cw2
=
F ca3
G = 0,8 kg
F = 0,2 m2
g = 9,81 m/s2
= 1,1 kg/m3
Wir erhalten aus dem Polardiagramm
Für den Vogel ohne Spreizung
Für den Vogel mit Spreizung
cw2
= 0,0216
c3
a min
cw2
= 0,0188
c3
a min
vsink = 1,23 m/s
vsink = 1,15 m/s
1000 m
a
Zeit: 13 min 33 sec
b
Zeit: 14 min 30 sec
EvolutionsWettkampf
Text
Es gibt viele Evolutionsstrategien
(1 + 1)-ES
(1 , l)-ES
(m , l)-ES
(m / , l)-ES
(1 + 1)-ES
DARWINs Theorie in
maximaler Abstraktion
(1 , l)-ES
l=6
Evolutionsstrategie mit mehr
als einem Nachkommen
(m , l)-ES
m=2
l=7
Evolutionsstrategie mit
mehreren Eltern und Nachkommen
(m / , l)-ES
m=2
=2
l=8
Evolutionsstrategie mit
Mischung der Variablen (Erbanlagen)
Entwicklung der Evolutionsstrategie
Darwin
Mendel
Populationsgegentiker
Wright Haldane Fisher
[ m / , l ( m / , l ) ] - ES
m' = Zahl der Eltern-Populationen
' = Mischungszahl Populationen
l' = Zahl der Nachkommen-Populationen
' = Zahl der Populations-Generationen
m = Zahl der Eltern-Individuen
= Mischungszahl Individuen
l = Zahl der Nachkommen-Individuen
= Generationen der Isolation
Auf dem Weg zu einer
evolutionsstrategischen
Algebra
Auf dem Weg zu einer evolutionsstrategischen Algebra
(1
ES
Wettkampfsituation
m +,+l12) - gliedrige
Auf dem Weg zu einer evolutionsstrategischen Algebra
( m /+,l) - ES
Beispiel = 2
(m / 2 +, l) - ES
Elter liefert nur die Hälfte der Erbinformation
Auf dem Weg zu einer evolutionsstrategischen Algebra
( m , l) - ES
+
Beispiel:
(1+ 6)4 = (1+ 6) (1+ 6) (1+ 6) (1+ 6)
Auf dem Weg zu einer evolutionsstrategischen Algebra
l ( m , l) - ES
+
Beispiel:
2 , 4(1, 6)
8 = (1, 6)8 + (1, 6)8 + (1
, 6)8 + (1, 6)8
Auf dem Weg zur geschachtelten Evolutionsstrategie
[ m , l ( m , l) -] ES
+
+
m' = Zahl der Eltern-Populationen
l' = Zahl der Nachkommen-Populationen
' = Zahl der Populations-Generationen
m = Zahl der Eltern-Individuen
l = Zahl der Nachkommen-Individuen
= Generationen der Isolation
Biologische Entsprechung der Strategie-Schachtelung
| FamilieGattung{Art[Varietät(Individuum)] }|
Vier Bergsteiger, vier Kletterstile
Verschiedene
Mutationsschrittweiten
Verschiedene
Strategien
In kompakter Notation
Geschachtelte Evolutionsstrategie
Angsthase
Kolumbus
N
Amundsen
Heißsporn
Vier Bergsteiger, vier Kletterstile
[ m , l ( m , l ) ] ES
m=1
l = 2
m =1
l =5
=4
Geschachtelte Evolutionsstrategie
(Gruppenevolution)
Neue Gründerpopulationen
Evolutionsstrategische Optimierung eines
Biegebalkens mit minimalem Gewicht
Evolutionsstrategische Optimierung eines
Fachwerk-Krans mit minimalem Gewicht
Evolutionsstrategische Optimierung einer
Fachwerkbrücke mit minimalem Gewicht
Brücken
Konstruktionen
Fischbauchbrücke
Bogenbrücke
Melancholie, Kupferstich von
Albrecht Dürer aus dem Jahr
1514
Magisches Quadrat
2012
Text
n2 n3
n4 n5 n6
n7 n8 n9
1
Qualitätsfunktion für ein 3 3-Quadrat
Q = (n1 n2 n3 15 )2 (n4 n5 n6 15 )2 (n7 n8 n9 15 )2
(n1 n4 n7 15 )2 (n2 n5 n8 15 )2 (n3 n6 n9 15 )2
(n1 n5 n9 15 )2 (n3 n5 n7 15 )2 Min
Hermann von Helmholtz 1821-1874
„Einen Naturvorgang verstehen heißt,
ihn in die Mechanik zu übersetzen“
Streitfall Evolution
Ende
www.bionik.tu-berlin.de
Zu Bob Shaws Erzählung „Andere Welten, andere Augen“
Was zunächst nur ein kurioser Nebeneffekt war, der einige Verkehrsunfälle und den Absturz
eines Testflugzeuges verursachte, wird zu einer Revolution, die die Welt ähnlich grundlegend
verändert wie die Erfindung der Dampfmaschine. Die Rede ist vom so genannten Langsamglas, Retardit genannt, das die Fähigkeit besitzt, Licht zu verlangsamen. Lichtstrahlen, die auf
diese Kristalle treffen, brauchen, je nach Typ des Retardits zwischen Sekundenbruchteilen bis
hin zu einigen Jahren, um es zu durchqueren. Ihren Erfinder machen diese Retardit-Scheiben
zu einem schwerreichen, doch unglücklichen Mann; denn bei dem Versuch, die Emission des
Lichts zu beschleunigen, um die gespeicherten Bilder früher abzurufen, kommt es zu einem
Blitz, der seiner Frau das Augenlicht nimmt. Da wird zum ersten Mal deutlich, dass Retardit
mehr kann, als nur Fenster mit Meerblick in die Großstadt zu bringen. Ärzten gelingt es, Retardit-Linsen anzufertigen, die eingefangenes Licht unter Umgehung der Netzhaut mit 24-stündiger Verspätung sichtbar machen. Das heißt, ein Mensch "lädt" die Linsen einen Tag lang auf,
dann werden sie eingesetzt und geben ihre Bilder frei. Verkehrsbeleuchtung, Spionagetechnik,
Verbrechensbekämpfung, bald ist Retardit nicht mehr wegzudenken aus der Welt…
Es sind die Winkeleinstellungen gesucht, bei der das Plattensystem im
Luftstrom des Windkanals den geringsten Widerstand aufweist. Die Lösung
der Aufgabe ist selbstverständlich im voraus bekannt. Die ebene parallel
angeströmte Platte (alle Winkel 180°) besitzt den geringsten Widerstand.
Es geht in dem Experiment darum, zu beweisen, dass diese Lösung nach
dem DARWINschen Prinzip auch gefunden wird (experimentum crucis).
Gesucht ist die Form einer rechtwinkligen Rohrumlenkung mit minimalen Strömungsverlusten. – Zum Versuchsaufbau: Ein flexibler Plastikschlauch wird
zunächst in der Anlaufstrecke der Strömung in einem geraden Rohr geführt,
dann in der Umlenkstrecke durch sechs verschiebbare Stangen gehalten und
schließlich in der nachfolgenden Beruhigungsstrecke wieder in einem geraden
Rohr geführt. Die sechs manuell verschiebbaren Stangen bilden die Variablen
des Systems. Die Rohrstrecke ist doppelt ausgeführt. Beide Rohre werden vom
selben Druckkessel gespeist. Ein Rohr ist der Elter, das andere Rohr der mutierte Nachkomme. Am Ende der Versuchsstrecke sind im Zentrum der Beruhigungsrohre zwei Pitotrohre platziert. Ihre Druckdifferenz zeigt an, ob sich der
mutierte Krümmer gegenüber dem Elter verbessert oder verschlechtert.
Es stehen 350 Segmente mit konischen Bohrungen zur Verfügung. Der
Durchmesser der Düse wird an einer Stelle mutativ verändert, indem jeweils
zwei Ringe ausgetauscht werden. Bei richtiger Wahl der Ringe kann erreicht
werden, dass die Anschlussdurchmesser links und rechts von der Mutationsstelle keinen Sprung erzeugen, während sich an der Berührungsstelle der
beiden neuen Segmente beidseitig der mutierte Durchmesser befindet.
Neue Generation
Der Computer gibt die Protokollblätter aus, auf denen die von dem Programm berechneten Anstell- und den
Staffelungswinkel der 5 Flügelohren von 12 Nachkommen ausgedruckt sind.
Nachkommen realisieren
Der Experimentator realisiert die Anstell- und Staffelwinkel an den Modelltragflügeln von 12 Nachkommen. Die
Verstellbarkeit ergibt sich durch der Verwendung von Bleistreifen an den Wurzeln der Flügelohren.
Auftriebs und Widerstand messen
Der Experimentator misst für jede Tragflügel den Auftrieb und den Widerstand. Er errechnet daraus den
dimensionslosen Auftriebs- und Widerstandsbeiwert (ca und cw).
Nachkommen bewerten
Der Experimentator berechnet für jeden im Windkanal vermessenen Tragflügel das Verhältnis cw2 / ca3
Je kleiner dieses Verhältnis ist, um so geringer ist die Sinkgeschwindigkeit des Flügels im Fluge.
Eltern eingeben
Der Experimentator sucht die 4 besten Tragflügeleinstellungen heraus. Er gibt die Nummern der Protokollblätter der 4 besten Nachkommen über die Tastatur in den Computer ein. Das Computerprogramm mischt
und mutiert die Werte der Anstell- und Staffelwinkel.
Zwei Vögel sind in der Tagesthermik 1000 Meter hoch gestiegen. Sie sind
müde und gleiten nun ohne Flügelschlag zu Boden. Vogel a (er könnte aus
den Anfängen der Vogelevolution stammen) besitzt noch keine Flügelspreizung. Vogel b ist „durchevolutioniert“. Seine Schwungfederkonfiguration ist
für geringstes Sinken optimiert. Wie viel mehr Zeit ist Vogel b länger in der
Luft als Vogel a?
Mit den Daten aus dem Polardiagramm errechnet sich für den Vogel b eine gegenüber dem Vogel a verlängerte Gleitzeit von 57 Sekunden. Das ist energetisch
ein Vorteil. Vielleicht entdeckt Vogel b gerade in dieser ihm von der Evolution
geschenkten Zeit noch eine Maus, die er zum Abend verspeist, während Vogel b
leer ausgeht.
Es soll ein Magische Quadrat mit 21 21 Feldern entwickelt werden. Die Summe der Zeilen, der Spalten und der Hauptdiagonalen soll jeweils 2009 betragen.
Und in der Mitte des Quadrats soll sich, wie im DÜRER-Quadrat, die Jahreszahl
2009 markieren. Die Figuren einer Zwei, Null und Neun mögen durch eine Serie
der Ziffern 2, 0 und 9 gebildet werden. Es handelt sich bei der Lösung zwangsläufig um ein so genanntes unechtes Magisches Quadrat, da Zahlen doppelt
vorkommen können und müssen.