PP-Präsentation des Vortrags

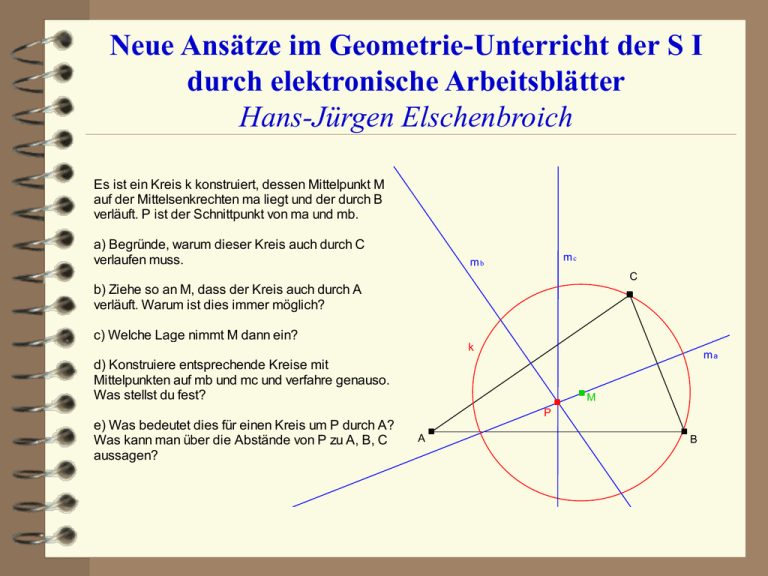
Neue Ansätze im Geometrie-Unterricht der S I
durch elektronische Arbeitsblätter
Hans-Jürgen Elschenbroich
Es ist ein Kreis k konstruiert, dessen Mittelpunkt M
auf der Mittelsenkrechten ma liegt und der durch B
verläuft. P ist der Schnittpunkt von ma und mb.
a) Begründe, warum dieser Kreis auch durch C
verlaufen muss.
mc
mb
C
b) Ziehe so an M, dass der Kreis auch durch A
verläuft. Warum ist dies immer möglich?
c) Welche Lage nimmt M dann ein?
k
ma
d) Konstruiere entsprechende Kreise mit
Mittelpunkten auf mb und mc und verfahre genauso.
Was stellst du fest?
M
P
e) Was bedeutet dies für einen Kreis um P durch A?
Was kann man über die Abstände von P zu A, B, C
aussagen?
A
B
Inhalt
 Geometrie-Unterricht und DGS
 Bewegliche Geometrie: (k)eine neue Idee
 Dynamischer Invarianz-'Beweis‘
 Visuell-dynamische Beweise
 Neue Ansätze: Elektronische Arbeitsblätter
 Verändertes Lernen
 Verändertes Lehren
 Beispiele
Geometrie-Unterricht und DGS
Werkzeuge im Geometrie-Unterricht:
• Zirkel, Lineal, Geodreieck
• Geometrie-Software der 1. Generation
• Dynamische Geometrie-Software (DGS)
Unterrichtlicher Einsatz von DGS:
• Neue Möglichkeiten
• Probleme und Vorbehalte
Behandlung von Standardthemen in moderner Sicht
in stabiler Lernumgebung!
Bewegliche Geometrie: (k)eine neue Idee
“Als einer der Hauptunterschiede altgriechischer und
neuzeitlicher Geometrie gilt das, daß in jener die
Figuren sämtlich als starr und fest gegeben
angenommen werden,
in dieser als beweglich und gewissermaßen fließend, in
stetem Übergang von einer Gestaltung zu anderen
begriffen. ...
Der Auffassung der Figuren als starrer Gebilde kann
und muß in verschiedener Weise entgegen gearbeitet
werden. Das eine hierzu Erforderliche ist das
Beweglichmachen der Teile einer Figur ... .”
Peter Treutlein, 1911
Dynamischer Invarianz-‘Beweis‘
Das Feststellen einer Invarianz im Zugmodus bleibt auf
der Stufe der experimentellen 'Beweise'
(vgl. Wittmann/Müller und Blum/Kirsch).
dynamischer Invarianz-'Beweis‘ (Elschenbroich)
Keine Antwort auf die Frage nach dem „Warum?“
Visuell-dynamischer Beweis
Präformale, visuell-dynamische Beweise:
• visuell: anschaulich, auf eine Zeichnung bezogen als
Figur, Eigenschaften und Bezeichnung
• dynamisch: keine einzelne, starre Zeichnung, sondern
eine ideale Zeichnung, eine ganze Klasse von
Zeichnungen, ermöglicht und sichtbar gemacht durch
den Zugmodus von DGS
• Beweis: ein vollgültiger Beweis in dem Sinne, dass er
nicht durch rationale Argumentationen zu erschüttern
ist und eine Antwort auf die Frage 'Warum' gibt.
Neue Ansätze: elektr. Arbeitsblätter
Vom Konstruieren von Figuren
. . . zum Arbeiten mit Figuren
Analogie zur Informatik
Elektronische Arbeitsblätter als „mediale Brücke“
Gefahr bei der Konstruktion von el. AB:
- klammheimliche Voraussetzungen
- Engführung/ Offenheit; unterrichtliche Robustheit.
Gefahr beim Unterrichten mit el. AB:
- Angst des Lehrers vor der eigenen Überflüssigkeit.
- Einengung auf nur eine ‚richtige‘ Lösung.
Verändertes Lernen
• handelnd statt passiv zuhörend
• eigenständigeres Arbeiten
• kooperatives Lernen
• entdeckendes Lernen
• mehr visuelle, heuristische & experimentelle Anteile
• Dokumentation, Präsentation
Verändertes Lehren
• Beobachten und Beraten.
• Aufgaben öffnen, Differenzierungsangebote.
• Wissensbasis der Schüler organisieren.
• Fehler als Chance.
• Methodenkompetenz vermitteln.
• Auch Selbstkontrolle der Schüler ermöglichen.
• Andere Formen der Bewertung und Leistungsüberprüfung.
Beispiele
Beispiele von Schüler-Arbeitsblättern
Beispiele von Lehrer-Seiten.
Die Beispiele können im Internet von der Mathe-Werkstatt
geladen werden.
http://www.mathe-werkstatt.de/download.htm
Literatur
Blum, Werner/ Kirsch Arnold: Warum haben nicht-triviale Lösungen von f ' = f keine
Nullstellen? Beobachtungen und Bemerkungen zum 'inhaltlich anschaulichen' Beweisen.
In: Kautschitsch/ Metzler: Anschauliches Beweisen.
Elschenbroich, Hans-Jürgen: Geometrie beweglich mit Euklid. Dümmler, Bonn 1996.
Elschenbroich, Hans-Jürgen: Dynamische Geometrieprogramme: Tod des Beweisens oder
Entwicklung einer neuen Beweiskultur? In: MNU 8/ 97.
Elschenbroich, Hans-Jürgen:Visuelles Beweisen - Neue Möglichkeiten durch Dynamische
GeometrieSoftware. In: Beiträge zum Mathematikunterricht 1999.
Elschenbroich, Hans-Jürgen/ Seebach, Günther: Dynamisch Geometrie entdecken.
Elektronische Arbeitsblätter mit Euklid, Klasse 7/8. Dümmler-Stam, Köln 1999.
Freudenthal, Hans: Was beweist die Zeichnung? In: mathematik lehren, Heft 17/ 1986.
Kautschitsch, Hermann: Wie kann ein Bild das Allgemeingültige vermitteln?
In: Kautschitsch/ Metzler: Anschauliches Beweisen.
Wittmann, Erich Christian; Müller, Gerhard: Wann ist ein Beweis ein Beweis? In:
Mathematikdidaktik: Theorie und Praxis. Festschrift für Heinrich Winter. Cornelsen,
Berlin 1988.