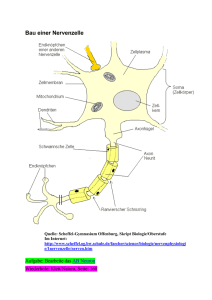
From Real Neurons To Perceptrons

From Real Neurons To
Perceptrons
Jacob Schroder
Überblick
 Die Modellierung eines echten biologischen Neuron
 Die bio-chemische elektrische Eigenscaften eines Neuron
 Wie diese Eigenschaften sich modellieren lassen
 Fazit: Perceptron != Neuron
 Frage: Gibt es eine Biologische Analogie von
Perceptrons?
 Populationmodellierung von Neuronen
 Fazit: Wie Populationmodellierung ähnlich wie
Perceptrons ist
Die Zellmembran
• Elektrische Eigenscaften eines
Neuron
– Zellmembran ist eine 3-4 nm
dichte Lipid-doppelschicht
– Die Membran ist der Schlüssel
zu den interessanten elektrischen
Eigenschaften eines Neuron
Die Membran II
• Die Membran ist undurchlässig für die meisten
Ions
– Diese Isolierungseigenschaft impliziert dass die
Membran wie ein Kondensator funktionert
– Ionkanäle lassen Ions zu über die Membran zu gehen
• Membrankapazitanz
• Membranpotential ist dann variabel
• Der Gliechgewichtpunkt einens Neurons
• Normaleweise wenn ein Neuron inaktiv ist hat
das Neuron eine negative Ladung
Elektrische Werte eines Neuron
– Membrankapazität = Cm
• Spezifische Membrankapazität cm = Cm /A
– Membranpotential = V
– Membranwiderstand = Rm
• Spezifische Membranwiderstand rm = Rm /A
– Membranzeitkonstante = tm = RmCm
Variabeles Membranpotential
dV dQ

• Cm
dt
dt
1.1
– Wieviel Strom ist erforderlich um Membranpotential
zu einer gegebenen Rate zu ändern
– dQ/dt = eingehender Strom
• Was kann das Membranpotential ändern?
–
–
–
–
Diffusion
Äusserer eingehender Strom
Synapses
Ionkanäle abhängig von Elektrischer Spannung
Welche Kräfte Sind an
Die Bewegung von Ions Beteiligt
• Diffusion
• Der Unterschied zwischen der Ladung innerhalb
des Neuron und ausserhalb des Neuron
• -[Membranpotentials] ziehen +Ions in dem
Neuron, und stossen -Ions aus dem Neuron ab
• Konzentration differences
– Na+ und Ca+2 sind konzentrierter draussen und K+
konzentrierter drinnen
• Ionpumps: Na/K ist am wichtigsten; gibt’s andere
Modellierung von Membrandiffusion
• Gleichgewichtpotential, E, ist sehr wichtig für die
Modellierung von Diffusion
– Das Berechnen dieses Werts ist wie wir Diffusion
modellieren werden
• Zwei Kräfte sind an die Bewegung von Ions in
Diffusion beteiligt
1. Konzentrationgradient
2. Kraftbarriere wegen der Membranpotential
Kraftwerte für Ions
• Einerseits: Gegeben R als die universale Gaskonstante
und eine normale Temperatur hat ein Mol Ions RT Kraft
• Anderseits: Ist die thermische Kraft von einem Mol Ions
= die Kraft verloren oder zugenommen wann ein Mol
Ions über die Membran geht = FVT
– F ist die Faradaykonstante und ist definiert als (Avagodros
Number) * (Die Ladung eines Protons)
– VT ist das Potential über die Membran
RT
• FVT = RT ergibt, VT 
F
1.2
Membrandiffusion II
• Wahrscheinlichkeit dass ein Ion innerhalb der Zelle die
Kraft hat um die Kraftbarriere zu überschreiten
– Gegeben dass eine positive Ion die Ladung, zq, hat und dass V
negativ ist
• q ist die Ladung eines Protons und z ist variabel
=> dass ein Ion die thermische Energie von -zqV haben muss um
die Membran zu überschreiten
=> dass die Wahrscheinlichkeit dass ein Ion diese Kraft hat wenn
die Temperatur T ist, = exp(zqV/kBT)
• kB ist die Boltzmann Konstante
– Diese Wahrscheinlichkeit ist in Molgewicht
exp(zFV/RT) = exp(zV/VT)
Membrandiffusion III
• [inside] = Ionkonzentration innerhalb der Zelle
– Die Rate dafür Ions aus der Zelle fliessen ist proportional zu
[inside]*Boltzmann-Konstante
• [outside] = Ionkonzentration ausserhalb der Zelle
– Die Rate dafür Ions in die Zelle fliessen ist proportional zu
[outside]
=> [outside]  [inside ] exp( zE / VT )
– Sei E das Membranpotential die die Gleichung erfüllt
VT  [outside] 

ln 
• 5.3 nach E aufgelöst ergibt E 
z  [inside ] 
– V wird zum E oder Umkehrungpotential hingezogen
1.3
• Man kann E für individuelle Ions berechnen
– Vereinfachung: wir benutzen nur ein E das nur einen
durchschnittlichen Wert für alle Ions representiert
=> Kapazität durchschnittlicher Wert für alle Ionkanäle
• Ein Ions E zieht V zu seinem E hin
–
–
–
–
Wenn V > E fliesst positiver Strom ausser dem Neuron
Wenn V < E fliesst positiver Strom im Neuron ein
E von Na+ and Ca+2 ist +, und depolarisiert ein Neuron
E von K+ ist -, und hyperpolarisiert ein Neuron
• Während eines Aktionpotential
– Depolarisieren Na+ und Ca +2 das Neuron und danach
K+ hyperpolarisiert das Neuron
Membranstrom = Im
• Im = der gesamte Strom der über die Membran
fliesst
– Einschliesslich Ionkanäle und äusserer Input
• im = Im/A
– Spezifischer Membranstrom
• im 
 g (V  E )
i
i
i
1.4
– gi ist der spezifische Leitwert je Flächeneinheit für eine
(oder mehrere) Art Ionkanal, i
Single Compartment Model
(Einzelabteil-Modell)
• Modellierung von elektrotonik kompakten
Neuronen
– Elektrotonik kompakt heisst ein Neuron das ein relativ
gleichmässiges Membranpotential hat
• Modell ist eine Vereinfachung
– Ignoriert Synapses und Ionkanäle abhängig von
Elektrischer Spannung
– Intrazellularwiderstand kann grosse Unterschiede in der
Membranpotential verursachen
• Einzelabteil Modell kann doch sehr nützlich sein
Das Modell
dV dQ
• Nochmal, C m

dt
dt
1.1
– Beschreibt das wesentliche Beziehung für Änderungen
im Membranpotential
dV
Ie
 im 
• Geteilt durch A, cm
1
.
5
dt
A
Integrate and Fire Modell
• Erweiterung des Einzelabteil-Modell
– Neuron kann ein Aktionpotential feuern
– Aktionpotential ist wann
1. V folgt eine “rapid stereotyped Trajectory”
2. V kehrt zu einem Wert zurürck der hyperpolorisiert
relativ zu dem Schwellwert ist
• Der gesamte Membranleitwert wird als einen
einzelnen Wert, gL, modelliert im  g L (V  E L )
• Wann V Vth dann feuer!
– Nach dem Feuern, V = Vreset, wo Vreset < Vth
Das Modell
dV
Ie
  g L (V  EL ) 
1.6
• cm
dt
A
• Wesentliche Integrate and Fire Gleichung ist
1.6*rm
dV
tm
 EL  V  Rm I e
dt
– Widerstand = 1/Leitwert, d.h. rm  1 / g L
– rm/A = Rm
1.7
Das Passiv oder
Leaky Integrate and Fire Neuron
• Modelliert unterhalb dem
Schwellwert
Membranpotentials für
manche Neuronen sehr gut
• Das Neuron benimmt sich
wie ein Kondensator und
ein Drahtwiderstand die
parallel sind
Feuerfestigkeit – “Refractoriness”
• Grundlegende Eigenschaft von echten Neuronen
• Leichte Lösung - Ein Neuron darf nicht für eine
bestimmte Zeit nach einem Aktionpotential feuern
• Eine realistischere Lösung ist die Hinzufügung von
einem neuen Leitwert
dV
tm
 E L  V  rm g sra (V  E K )  Rm I e
dt
–
–
–
–
1.8
Gleichung 5.8 mit einem neuen Strom, gsra
Wann ein Neuron feuert: gsra => gsra + Δgsra, Δgsra gross
Neuron zum Δgsra für eine Zeitkonstante befestigt
gsra ist von einem K+ Leitwert modelliert
Cabel Equation (die Kabelgleichung)
• Die Modelleriung von Dendrits und Axons
– Diese neuronalen Strukturen sind normaleweise dunn
genug dass wir die radiale Ekkeften auf dem Strom
ignorieren können weil sie unbedeutend im Vergleich
mit den entlanglaufenden Effekten sind
• Dendrits und Axons benehmen sich wie ein
Koaxialkabel
• Ladung in den Dendrits und Axons sind eine
Funktion, V(x,t), von Längsposition und Zeit
– x ist die Längskoordinate und t ist Zeit
– Einfliessender Strom ist positive und ausfliessender
Strom ist negativ
Das Modell
•
•
•
•
Ziel: Änderungsrate für das Membranpotential
Erst berechnen wir IL, entlanglaufender Strom
Längswiderstand ist RL  rL x /(a 2 )
ΔV= - RLIL
– Beziehung zwischen ΔV und RL kommt von Ohmsches
Gesetz
• Impliziert
V  rL xI L /(a 2 )
1.9
• Nach IL aufgelöst & den Grenzwert für x gegen 0 ergibt
I L  a V /( rL x)
2
 a V
IL 
rL x
2
lim
x  0
1.10
Modell II
• Die Änderungsrate von V hängt von der Kapazität
ab
– Die Menge von erforderlichem Strom um V zu einer
bestimmten Rate zu ändern ist
2axcm V / t
• Für die gesamte Kablegleichung brauchen wir eine
Gleichung die beschreibt wie die verschiedenen
ein/ausfliessenden Ströme und entlanglaufende
Ströme das Differential von V beeinflussen
Alles Zusammen!
• Die verschiedenen Ströme die Membranpotential
ändern können wird in dieser Graphik gezeigt
• Die Ströme vom Diagramm addiert ergibt
 a 2 V 
 a 2 V 
V
  

2axcm
  
 2ax(im  ie )
t
 rL x  left  rL x  right
1.11
• Vereinfachung von 2 Termen; geteilt durch 2ax
 a 2 V   lim x  0   a 2 V 
1  a 2 V 


    

 
x  rL x  right  rL x  left 
x  rL x 


• Die Wesentliche Kabelgleichung
V
1   2 V 
cm

a
  i m  ie
t 2arL x  x 
1.12
Attenuation - Schwächung
I e R
 | x |
v( x) 
exp  

2
  
1.13
– Eine Lösung zur
Kabelgleichung mit
konstanter Stromspritze
auf einem Punkt, 0
• Exponentielle
Abschwächung des
Signals
• Vermüteter Grund für die
biologische Motivation
für Spiking
Randbedingungen für die
Kablegleichung
• Für ein gespaltetes Kabel
– Die Potential muss stetig sein: V(x,t) muss in jedem
Teil des Kabels definiert sein so dass wo die Teile
des Kabels sich treffen das Ergebnis von V(x,t) für
jedes Kabel gleich ist
– Die Summe von entlanglaufendem Strom in jedem
Teil des Kabels muss bei dem Verbindungspunk
gleich 0 sein
• Sei der Strom nach dem Ende des Kabels
einfach gleich 0
Fazit: Perceptron != Neuron
 Wir haben gesehen
 Ein Modell für elektrotonik kompakte neuronale
Teilfläche, das Single Compartment Model
 Ein Modell für dendritische und axonische Segmente
eines Neuron mit der Kabelgleichung
 Folgerung ist dass ein Model eines echten Neuron
ist unbedingt anders als ein Perceptron
Frage
 Gibt es eine Biologische Analogie von Perceptrons?
Eine Deterministiche
Populationmodellierung von Neuronen
 Prämisse
 Neuronen sind relativ in der Nähe von einander
 Verbindungen sind willkürlich und dicht
 Daraus folgen dass es einen Weg von jedem Neuron zu jedem
anderen Neuron gibt, egal wenn dieser Weg durch ein Paar
andere Neuronen führt
=> Wir ignorieren die räumliche Aspekte der
Modellierung
 Alle neuronalen Prozesse sind Interaktionen zwischen
hemmenden und stimulierenden Neuronen, d.h. dass
wir nur diese zwei Typen von Neuronen modellieren
Das Modell
 E(t) = Proportion von stimulierenden Neuronen
die in einer Zeiteinheit ab Zeit, t, feuern
 I(t) = Proportion von hemmenden Neuronen die
in einer Zeiteinheit ab Zeit, t, feuern
 E(t) = 0 = I(t) ist der Rühezustand wo nur
Hintergrundaktivität passiert
 Neuronen sind noch aktiv, d.h. dass ein
negativer Wert einen Abfall von normaler
Aktivität bedeutet
Welche Proportion ist Feuerfest?
 Sei die absolute feuerfeste Periode = r
 Die Proportion von stimulierenden Neuronen die
feuerfest sind
t
 E(t ' )dt '
2.1
t r
 Proportion von stimulierenden Neuronen die nicht
feuerfest
sind
t
1
 E (t ' )dt '
t r
 Äquivalente Gleichungen für I(t)
2.2
Welche Proportion bekommt
mindestens Eingabe > Schwellwert?
 Erforderlich sind 2 Funktionen
 Se(x) = Erwartete Proportion von stimulierenden
Neuronen die mindestens Eingabe > Schwellwert
bekommen
 Si(x) = Erwartete Proportion von hemmenden
Neuronen die mindestens Eingabe > Schwellwert
bekommen
 Genannt “Subpopulation response functions”
Eine typische S(x)
 Se(x) und Si(x)
müssen sigmoidale
Funktionen sein
 S ist eine Funktion
von dem
durchschnittlichen
Level der Exzitation
Durchschnittlicher Level der
Exzitation eines Neuron
 Die Eingabe für S(x)
t
 a (t  t ' )c1 E (t ' )  c2 I (t ' )  P(t ' )dt '

2.3

 c1 und c2 sind die durchschnittliche Zahl von
stimulierenden und hemmenden Synapsen je Neuron
 P(t) ist die äussere Eingabe
 a(t) ist eine Abklingenfunktion, d.h. dass der Level der
Exzitation des Neuron fällt im Zeitablauf ab
 I(t) hat eine entsprechende ähnliche Gleichung,
aber mit eigenen P(t) und cX

t


2.4
E (t  t )  1   E (t ' )dt ' 
t r


t

S e   a (t  t ' )c1 E (t ' )  c2 I (t ' )  P(t ' )dt '
 

t


 I (t  t ' )  1   I (t ' )dt ' 
 t r

t

Si   a (t  t ' )c3 E (t ' )  c4 I (t ' )  Q(t ' )dt '
 

2.5
 Erste Gruppe von Termen ist die Proportion von
Neuronen die nicht feuerfest ist
 Zweite Gruppe von Termen ist die Proportion von
Neuronen die mindestens Eingabe > Schwellwert
Time Coarse Graining
 Idee - Wir wollen einen durchschnittlichen Wert
für eine Funktion über ein Intervall
1
f (t ) 
s
t

f (t ' )t '
2.6
t s
 Numerische Vereinfachung und glättet kurze
Schwankungen
t

 E(t ' )t '  r E(t )
2.7
t s
t
  a (t  t ' ) E (t ' )t ' 
 k E (t )

2.8
Die Gleichungen
 Nehmen die Taylorentwicklung weil Time
Coarse Graining glättet grosse Schwankungen
 Benutzen die 2 neuen Vereinfachungen von
dem lezten Slide

dE
  E  (1  r E ) Se kc1 E  kc2 I  kP(t )
t
dt


2.9

2.10
dI
  I  (1  r I ) Si k ' c3 E  k ' c4 I  k ' Q(t )
 t'
dt
Populationmodellierung
und Perceptrons
 Die letzte Gleichungen koennen auch in dieser Form
ausgedrückt werden
E
 - E  S ( aE  bI)
2.11
t





E ist die stimulierende Eingabe
I ist die hemmende Eingabe
kc1 => a
kc2 => b
P(t), t und die feuerfest Periode, (1-rEbar), lassen fallen
Populationmodelierung
und Perceptrons II
 E and I sind linear
 Nehmen den Grenzwert für t gegen , und dann
E
0
t
=>
E = S( aE + bI)
2.12
 Ist eigentlich die Perceptron Gleichung
 S ist die Ausgabefunktion für einen Perceptron
Kurzfassung
• Neuronen sind sehr komplexe Einheiten
– Die Lipid-Doppelschicht bewirkt viele komplexe Effekten
• Ein vereinfachtes Modell, Integrate and Fire Model
– Modelliert nur wesentliche Eigenschaften eines Neuron
– Kann Kapazität, Potential und Spiking gut modellieren
– Nicht ähnlich wie ein Perceptron
• Die Kabelgleichung für Dendrits und Axons
– Schlägt eine Antwort zu “Why Neurons Spike” vor
• Populationmodellierung bietet eine biologische
Analogie für Perceptrons
Danke für Ihre Aufmerksamkeit
• Quellen
1. Cowan, Jack D. and Wilson, Hugh R. Excitatory and
Inhibitory Interactions In Localized Populations of
Model Neurons. Biophysical Journal. 1972. Vol. 12.
2. Abbot, L.F. and Dayan, Peter. Theoretical
Neuroscience. MIT Press: London, England. 2001. p.
153-217.
Zusätzliche Folien
Spike-Rate Adaptierung
• Grundlegende Eigenschaft von echten Neuronen
– Wir brauchen einen detaillierteren Membranstrom
dV
tm
 E L  V  rm g sra (V  E K )  Rm I e
dt
– Gleichung 5.8 mit einem neuen Strom, gsra
– Wann ein Neuron feuert:
gsra => gsra + Δgsra
– gsra ist von einem K + Leitwert modelliert
• Wann es sich activiert, gsra hyperpolisiert das Neuron und
dadurch verlangsamt irgendeines Aktionpotential
• gsra fällt für Zeitkonstante, tsra, ab, t sra
dg sra
  g sra
dt
Spike-Rate Adaptierung II
• b ist eine Aufnahme von einem Kortikalneuron mit
konstantem Stromsprizte das Spike Rate
Adaptierung zeigt
• c ist unseres Modell mit den Werten
– rmΔgsra = 0.06,
tsra = 100ms,
Ek = -70mV
Die Feuerrate
• Could eliminate?
• Gleichung 5.8 nach V(t) aufgelöst ergibt,
V (t )  E L  Rm I e  (V (0)  E L  Rm I e ) exp( t / t m )
– Gilt nur wenn das Neuron unter den Schwellwert ist
und wenn Ie unabhängig von Zeit ist
• Gegeben dass
– t=0, das Neuron gerade feuerte und V = Vreset, und tisi
die Zeit ist wann das nächste Aktionpotential
passieren wird
V (t isi )  Vth  E L  Rm I e  (Vreset  E L  Rm I e ) exp( t isi / t m )
Feuerrate II
• Nach tisi aufgelöst ergibt,
 Rm I e  E L  Vreset
1 
risi 
 t m ln 
t isi 
 Rm I e  E L  Vth

 


1
– Ergibt die “Interspike interval firing rate” für konstant Ie
• Gegeben einen genügend grossen Ie
 Rm I e  E L  Vth 
risi  

 t m (Vth  Vreset ) 
– Benutzt die lineare Approximation,
ln(1+z) = z, für klein z