Entwicklung der Beschleuniger und Beschleunigertypen
Werbung

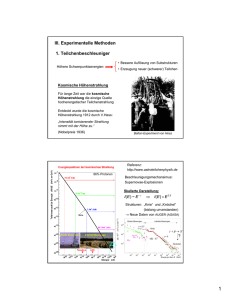
Kapitel 4 Entwicklung der Beschleuniger und Beschleunigertypen Rüdiger Schmidt (CERN) – Darmstadt TU - Februar 2010 - Version 2.3 Übersicht Gleichspannungsbeschleuniger HF – Beschleuniger Linearbeschleuniger Zyklotron Synchrotron Speicherring Beispiel eines Beschleunigerkomplexes am CERN: LEP / LHC und Vorbeschleuniger 2 Gleichspannungsbeschleuniger: Cockcroft–Walton und Van de Graaff Generator Im Jahre 1929/30 begann J.D.Cockcroft und E.T.S.Walton (Cavendish Labor, E.Rutherford) als auch R.J.Van de Graaff (Princeton) mit der Arbeit Hochspannungsgeneratoren, die eine Spannung bis zu 10 MV erreichten. The tandem Van de Graaff accelerator at Western Michigan University is used mainly for basic research, applications and undergraduate instruction. 3 4 Vom Gleichspannungsbeschleuniger zum HF Beschleuniger • Die Grenze von Hochspannungsanlagen liegt bei einigen Millionen Volt. Die Anlagen werden für höhere Energie immer aufwendiger, und bei höherer Spannung kommt es zu Funkenüberschlägen. • Vorschlag vom Schweden Ising 1924, zur Beschleunigung anstatt Gleichspannung schnell wechselnde Hochfrequenzspannung zu benutzen. • Der Norweger Wideröe 1928 testet erfolgreich den ersten Linearbeschleuniger, der auf diesem Prinzip beruht. • Heute arbeiten fast alle Beschleuniger mit Hochfrequenzspannung zur Beschleunigung 5 Beschleunigung mit einem hochfrequenten elektrischen Feld Zeitlich veränderliche Spannung: ( U ( t ) := U 0 sin 2 p f rf t ) f rf = 100 MHz Frequenz : Maximale Spannung: 6 U 0 = 1 10 V U(t) Spannung 6 1 .10 5 .10 5 0 5 .10 5 1 .10 6 1 .10 8 5 .10 9 0 Zeit 5 .10 9 1 .10 8 6 Linearbeschleuniger (LINAC) l1 l2 l3 l4 l5 l6 l7 Teilchenquelle Driftröhren aus Metall • • • • ~ HF-Sender mit fester Frequenz Teilchen treten aus der Quelle aus und werden vom Potential der ersten Driftröhre beschleunigt Während die Teilchen durch die erste Driftröhre laufen, kehrt sich das Vorzeichen des Potentials um Teilchen treten aus der ersten Driftröhre aus und werden durch das Potential der zweite Driftröhre beschleunigt Da die Geschwindigkeit der Teilchen steigt, wird der Abstand zwischen zwei Röhren grösser 7 li Energie des Teilchens nach der Röhre i: Ei = i e0 U0 sin(s ) + 1.1 1.1 0.55 sin ( r) 0 0.55 1.1 1.1 6.28 4.71 3.14 1.57 0 1.57 3.14 4.71 rrr 2p 6.28 2 p x Sine function dabei ist U0 die maximale Spannung des HF Senders, und s die mittlere Phase mit der das Teilchen die Strecke zwischen den Röhren passiert. + 1.1 1.1 0.55 sin ( r) 0 0.55 1.1 1.1 3.14 1.57 0 1.57 3.14 rrr 1p x Sine function 4.71 6.28 7.85 9.42 3 p Konsequenz: es lässt sich kein kontinuierlicher Strahl beschleunigen, die Teilchen werden im Paketen (Bunch) beschleunigt (Bunchlänge von weniger als 1mm bis zu 1m) Linearbeschleunigers am FERMILAB 1971, upgraded in 1993 Linac can accelerate beam to 400 MeV Low energy end of the Fermilab linac is an Alvarez style drift tube linac. The accelerating structures are the big blue tanks shown in the photo. The five tanks of the low energy end take the beam from 750 KeV to 116 MeV. The resonant frequency of the cavities is 200 MHz. Struktur eines Linearbeschleunigers am FERMILAB Hohlraumresonantor (cavity) Standing wave Travelling wave 11 Kreisbeschleuniger: Zyklotron Für ein Teilchen dass sich senkrecht zum Magnetfeld bewegt: F = m a = q v B z s daraus ergibt sich eine Kreisbewegung des Teilchens: B dv m = q v B dt dv q = v B m dt v F Gleichgewicht zwischen Lorentzkraft und Zentrifugalkraft: x FLorentz = q v B FZentrifuga l = m v Die Zyklotronfrequenz ist unabhängig von Geschwindigkeit und Energie des Teilchens 2 R R = m v / q B v q mit = gilt : = B R m Bei zunehmender Energie und Geschwindigkeit läuft das Teilchen mit grösserem Radius im Magnetfeld um 12 Kreisbeschleuniger: Zyklotron Die Zeit für einen Umlauf ist konstant, daher ist auch die Frequenz der elektrischen Feldes für die Beschleunigung konstant. 13 Vertikale Fokussierung im Zyklotron People just got on with the job of building them. Then one day someone was experimenting The Figure shows the principle of vertical focusing in a cyclotron In fact the shims did not do what they had been expected to do Nevertheless the cyclotron began to accelerate much higher currents E.Wilson Lectures 2001 14 Beispiel für die Parameter eines Protronenzyklotron Annahme: Das Magnetfeld hat eine Stärke von maximal Bcyclotron := 1T e0 Die Umlauffrequenz ist durch: rev := Bcyclotron gegeben mp Damit ergibt die Frequenz von frev := rev 2p => frev = 15.244 MHz Bei einer kinetischen Energie von Ep := 20MeV ergibt sich der Radius des Zyklotrons: mit: Ep = r := v rev mp c 2 1b 2 v := c 1 folgt: 2 mp c 4 (Ep + mp c ) 2 2 , und Damit ist die Geschwindigkeit v = 6.093 10 7m s und der Radius r = 0.636 m 15 E.O Lawrence – Erfinder des Zyklotrons The inventor of the cyclotron, E. O. Lawrence, and his student E. McMillan, one of the two inventors of the principle of phase stability show the accelerating point at the entrance to a screened semi-circular electrode structure. www4.tsl.uu.se/~kullander/Nobel/index.html 16 Isochronzyklotron Wenn die Geschwindigkeit des Teilchens wächst, muss das Magnetfeld ebenfalls mit dem Radius anwachsen: q B(R) m B0 wächst mit (R) an = http://abe.web.psi.ch/accelerators/vortraegeWernerJoho/ 17 Zyklotron am CERN Zyklotron am PSI Medizin-Zyklotron des PSI wurde für die spätere Anwendung der Protonentherapie in Spitälern entwickelt, wiegt 90 t und hat einen Durchmesser von 3,2 m Protonen mit 60 Prozent der Lichtgeschwindigkeit Supraleitenden Spulen Physikern und Ingenieuren der Michigan State University, des PSI und der Firma ACCEL Instruments GmbH Ein zweites derartiges Zyklotron ist für das erste klinische ProtonentherapieZentrum in Europa, das in München gebaut wird, bei Accel zurzeit in der Fertigung. http://images.google.de/imgres?imgurl=http://ww w.ethlife.ethz.ch/images/psi_zyklotronl.jpg&imgrefurl=http://www.ethlife.ethz.ch/articles/ news/psi_zyklotron.html&h=1004&w=800&sz=405 &tbnid=mw0NqgE2g2cX9M:&tbnh=149&tbnw=118 &hl=de&start=2&prev=/images%3Fq%3Dzyklotron %2Bpsi%26svnum%3D10%26hl%3Dde%26lr%3D %26sa%3DG Superconducting Cyclotron and Fast Proton Beam Scanning for Hadron Therapy http://www.protonen-therapie.de/pg_0006.htm Advantages of a Cyclotron • Max. energy 250 MeV with fast energy variation by energy selection system • High availability / up-time • Reasonable investment / operating cost • Fast and simple maintenance procedures, small operator group • Low activation Advantages Using sc Magnet Coils • Make use of achievable high fields in larger volume to increase • gap size over full radius -> avoid nonlinearities -> improved extraction • efficiency to larger than 80% • No ohmic losses of Cu-coils -> less rated power needed and reduced electrical consumption • Closed cycle LHe operation -> easy maintenance • „Warm“ access as in a normalconducting cyclotron 20 Kreisbeschleuniger: Synchrotron Mit einem Zyklotron oder Betatron ist die Energie der Teilchen begrenzt • Man kann keine beliebig grosse Magnete bauen • Das Magnetfeld ist auf 1-2 Tesla (normalleitende Spule), bzw. 5-10 T (supraleitende Spule) begrenzt • Im Betatron kann die Beschleunigung nur über einen Teil eines Magnetzyklus erfolgen Um hohe Energien zu erreichen, wurde das Synchrotron entwickelt • Das Synchrotron ist der am meisten verbreitete Beschleunigertyp • Das Synchrotron ist ein Kreisbeschleuniger, in dem die Teilchen viele Umläufe machen • Im Synchrotron wird das Magnetfeld erhöht, und gleichzeitig werden die umlaufenden Teilchen beschleunigt • Die Teilchenbahn bleibt (ungefähr) konstant 21 Entwicklung des Synchrotrons • Vorgeschlagen 1943 von M.O.Oliphant • Entwicklung etwa gleichzeitig 1945 vom E.M. McMillan an der Universität von Kalifonien und V. Veksler in der Sowjetunion • Erstes funktionierendes Synchrotron (proof of principle) in England (Birmingham) von F.Goward und D.Barnes Energiegewinn durch elektrisches Feld, das Magnetfeld wird synchron dazu erhöht Magnetfeld Strahlintensität 450 GeV Extraktion Beispiel: CERN-SPS Protonensynchrotron 14 GeV Injektion Injektion Extraktion 14 sec Zyklus Zeit 22 Aufbau des Synchrotrons Komponenten eines Synchrotrons: • Ablenkmagnete • Magnete zur Fokussierung • Injektionsmagnete (gepulst) • Extraktionsmagnete (gepulst) • Beschleunigungsstrecke • Vakuumsystem • Diagnostik • Kontrollsystem • Stromversorgungsgeräte 23 CERN Protonensynchrotron (CERN-PS) gebaut 1959 24 Typical Synchrotron Magnet 25 Beschleunigung im Protonensynchrotron – CERN SPS I Die Länge des Beschleunigers ist L := 6911m und der Krümmungsradius der Ablenkmagnete ist r := 754m . Die Länge der Ablenkmagnete ist Ldipole := 2p r 3 => Ldipole = 4.738 10 m Der Impuls ist durch Stärke des Ablenkmagnetfeld und Krümmungradius r gegeben: p = r B e0 Einj := 14GeV und der Endenergie Etop := 450GeV ergibt sich bei Injektion das Feld in den Ablenkmagneten von Mit der Injektionsenergie von: Binj := Einj r e0 c und Btop := Etop r e0 c Magnetfeld bei Injektionsenergie: Binj = 0.062 T Magnetfeld bei Endenergie: Btop = 1.991 T 26 Beschleunigung im Protonensynchrotron – CERN SPS II L Die Magnetfeldrampe dauert etwa Tramp := 4s . Ein Umlauf dauert Trev := c (dabei wird v = c angenommen) Tramp Die Anzahl der Umläufe während der Rampe ist Nramp := und die Trev Energieänderung von Etop Einj = 436 GeV Für die Beschleunigung der Protronen Etop Einj pro Umlauf ist DEturn := erforderlich, Nramp ( ) 6 d.h. DEturn = 2.513 10 eV 27 Kreisbeschleuniger: Speicherring • Der Speicherring ist ein Sonderfall eines Synchrotrons • Die Teilchen werden in der Regel beschleunigt, und für lange Zeit (Stunden, oder sogar Tage) gespeichert • Wichtigste Anwendung von Speicherringen • Erzeugung von Synchrotronstrahlung • Erzeugung von neuen Teilchen Der grösste Kreisbeschleuniger war LEP. LEP wurde nach 12 Jahren Betriebszeit Ende 2000 abgeschaltet. In den LEP Tunnel mit einer Länge von etwa 27 km wurde der supraleitender Protonenbeschleuniger LHC installiert. LEP: Schwerpunktsenergie = 200 GeV Elektronen Positronen LHC: Schwerpunktsenergie = 14000 GeV Protonen Protonen 28 Um zu hohen Energien zu beschleunigen…..Beispiel LEP Beschleunigungsstrukturen (Hochfrequenz Cavities) werden in den meisten Beschleuniger benötigt • Normalleitende Cavities aus Kupfer: 1-2 MV/m lassen sich routinemässig erreichen. Mit gepulsten Cavities (z.B. SLAC) kommt man wesentlich höher – zwischen 50-80 MV/m (in der Entwicklung) • Supraleitenden Cavities: • • LEP (CERN – 2001): ILC : 5-8 MV/m etwa 35 MV/m Die Endenergie der e+ und e- Strahlen vom LEP Collider ist 100 GeV. Wenn der Beschleuniger als LINAC mit einer Technologie, die vor 15 Jahren zur Verfügung stand, gebaut worden wäre, hätte er eine Länge von: L = 100 GeV / 2.5 MeV/m = 40000 m für jeden der beiden Beschleuniger für Elektronen und Positronen – d.h. 80 km. Ausserdem wären die supraleitenden Cavities wesentlich teurer geworden. Schwerpunktsenergie im Zentrum = 200 GeV Elektronenlinac 40 km Positronenlinac 40 km 29 LEP Die Teilchen laufen bei jedem Umlauf durch die Beschleunigungsstruktur. Ein Umlauf dauert 89 s. In einer Sekunde macht ein Teilchen 11246 Umläufe, und läuft bei jedem Umlauf durch die Beschleunigungsstrecke. Während der Beschleunigung von 20 GeV auf 100 GeV wird das Magnetfeld in allen Ablenkmagneten von 0.024 Tesla auf 0.119 Tesla hochgefahren. LEP - Umfang 26.8 km etwa 4 Bunche / Strahl eine Vakuumkammer Die Magnetrampe dauert einige Minuten. 30 Magnetrampe bei LEP Der Impuls ist durch Stärke des Ablenkmagnetfeld und Krümmungradius r gegeben: p = r B e0 Mit der Injektionsenergie von LEP: Elep_inj := 20GeV und der Endenergie Elep_end := 100GeV ergibt sich bei Injektion das Feld in den Ablenkmagneten von Elep_inj Blep_inj := r e0 c und Blep_end := Elep_end r e0 c Magnetfeld bei Injektionsenergie: Blep_inj = 0.024 T Magnetfeld bei Endenergie: Blep_end = 0.119 T 31 Beschleunigung im Kreisbeschleuniger Für eine Dauer von 5 min für die Rampe: Nramp := 11246 Hz 300 s und die Energieänderung von 80 GeV ist eine Beschleunigung der Elektronen von DEturn Elep_end Elep_inj) ( := Nramp erforderlich, 4 d.h. DEturn = 2.371 10 eV Aus dieser Abschätzung sieht man, das pro Umlauf eine Spannung von einigen 10 kV ausreichen würde, um ein Teilchen von 20 GeV auf 100 GeV zu beschleunigen. In LEP haben die Beschleunigungsstrukturen jedoch eine Spannung von etwa 2-3 GV (!!) => Abstrahlung von Synchtrotronstrahlung 32 Konsequenzen der Abstrahlung von Synchrotronstrahlung • Zur Erzeugung von Synchrotronstrahlung werden Speicherringe für Elektronen und Positronen gebaut • Im LEP Tunnel lassen sich e+e- nicht auf höhere Energie als etwa 100 GeV beschleunigen, das der Energieverlust zu gross wird. Um zu höherer Energie zu kommen… • Im LEP Tunnel wird ein Protonenbeschleuniger, der LHC, installiert. Protonen lassen sich damit auf 7 TeV beschleunigen. • Um e+e- auf höhere Energie zu beschleunigen, werden Linearbeschleuniger entwickelt. 33 LHC Parameter The force on a charged particle is proportional to the charge, and to the vector product of velocity and magnetic field: F = q (E + v B) z s B v F • Maximaler Impuls 7000 GeV/c • Radius 2805 m B= p e0 R x • Ablenkfeld B = 8.33 Tesla • Magnetfeld mit Eisenmagneten maximal 2 Tesla, daher werden supraleitende Magnete benötigt 34 The CERN accelerator complex: injectors and transfer 5 LHC 4 Beam 1 Beam 2 6 7 3 2 SPS 8 TI8 TI2 Protons LINACS 1 Booster CPS Ions LEIR High intensity beam from the SPS into LHC at 450 GeV via TI2 and TI8 LHC accelerates to 7 TeV Beam size of protons decreases with energy: 2 = 1 / E Beam size large at injection Beam fills vacuum chamber at 450 GeV 35 CERN LHC accelerator complex ?? 36 ANHANG 37 Beschleunigung durch ein zeitlich veränderliches Magnetfeld: Betatron B(t ) E( t ) Vakuumkammer Ein zeitlich veränderliches Magnetfeld induziert im Vakuum ein elektrisches Feld nur im Script Eisenjoch Spulenwindung 38 Induktionsgesetz 2.Maxwellsches Gesetz E = rot E = B t (Induktionsgesetz) Integralform : E d r = BdS t B nur im Script Ein zeitlich veränderliches Magnetfeld induziert in einem Leiter einen elektrischen Strom 39 Betatron • Das erste Betatron wurde von D.W.Kerst 1940 an der Universität Illinois gebaut. Elektronen wurden bis 2.3 MeV beschleunigt. • Wenig später wurde ein Betatron mit einer Energie von bis zu 20 MeV realisiert. • Heute werden Betatrons insbesonders für medizinische Anwendungen benutzt. • Das Spulenfeld wird mit einem Wechselstrom erzeugt B = B 0 sin( t ) d 2 mit 2 p R E(t ) = p R B(t ) dt R d gilt für das elektrische Feld : E(t ) = B(t ) 2 dt nur im Script 40 Parameter eines Betatron Angenommen, das Magnetfeld wird mit einem kurzen Puls betrieben. In einer Zeitspanne von Dt := 5s wird das Feld um DB := 1T verändert. Der Radius des Beschleunigers ist: RB := 5m Damit folgt: RB DB Elektrisches Feld: EB := 2 Dt EB = 5 10 5 V m Elektrisches Feld um den Beschleuniger: EB_integral := 2p RB EB 7 EB_integral = 1.571 10 V nur im Script 41