I. Kriging

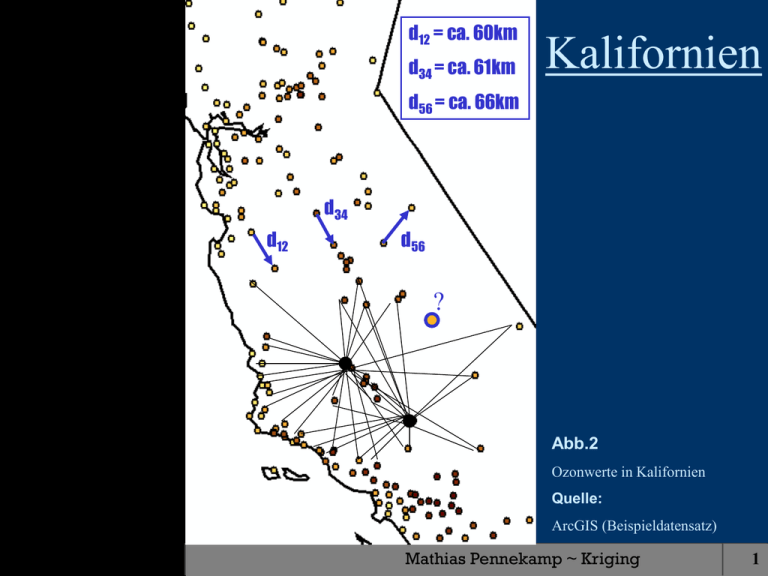
d12 = ca. 60km
d34 = ca. 61km
Kalifornien
d56 = ca. 66km
d34
d12
d56
?
Abb.2
Ozonwerte in Kalifornien
Quelle:
ArcGIS (Beispieldatensatz)
Mathias Pennekamp ~ Kriging
1
Geostatistik
2 Kriging
Mathias Pennekamp ~ Kriging
2
Inhaltsübersicht dieses Vortrags:
I. Einstieg in Kriging
- was ist Kriging
- Rückblick auf deterministische Verfahren
- Ziel des Krigings
II. Signalbehandlung
-
Statistische Grundbegriffe
-
Semivarianz
-
Semivariogramm
III. Kriging
-
Analysen im Semivariogramm
-
Beispielrechnung
-
verschiedene Krigingverfahren
-
ArcInfo
Mathias Pennekamp ~ Kriging
3
I. Kriging – Einstieg
-Der Name
:“Kriging“
-Rückblick
-Ziel
II. Signalbehandlung
-statistische
Grundbegriffe
-Semivarianz
Der Name: „Kriging“
Kriging (1)


Benannt nach D. G. Krige :
Bergbauingenieur, Südafrika
Kriging (2)

Oberbegriff für stochastische
Interpolationsverfahren

seit Anfang der 60er
-Beispielrechnung

entwickelt durch G. Matheron, Frankreich
-verschiedene
Krigingverfahren

-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
für geodätische Fragestellungen durch Krarup
und Moritz über Kovarianzfunktionen
weiterentwickelt (um 1969)
Man unterscheidet Kriging von den deterministischen
Verfahren.
Mathias Pennekamp ~ Kriging
4
I. Kriging – Einstieg
Rückblick: deterministische Verfahren
-Der Name
:“Kriging“
-Rückblick
-Ziel
II. Signalbehandlung
 Globale Methoden (z.B. Regression)
 Lokale Methoden (z.B. IDW, nearest neighbours)
-statistische
Grundbegriffe
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
Grundsätze:
 Bestimmung von Attributwerten [z] an nicht
beprobten Stellen (xu,yu)
 Flächenhafte Information aus Punktdaten (xi,yi)
 Verschiedene Möglichkeiten die Punktdaten (xi,yi)
zu berücksichtigen ( Gewichtung)
Mathias Pennekamp ~ Kriging
5
I. Kriging – Einstieg
Deterministisches Verfahren Gewichtung der Punktdaten
-Der Name
:“Kriging“
• Polynom-Interpolation
Unterschiedlich (Funktionswerte)
-Rückblick
• Invers distance weighting
Über die Distanz (i. A. Kehrwert)
-Ziel
• nearest neighbours
Einheitlich für Voronoi-Region
II. Signalbehandlung
-statistische
Grundbegriffe
?
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
?
?
-Beispielrechnung
-verschiedene
Krigingverfahren
 Bei deterministischen Verfahren wird subjektiv
gewichtet.
Kriging optimiert die Gewichtung der Punktdaten.
Mathias Pennekamp ~ Kriging
6
I. Kriging – Einstieg
-Der Name
:“Kriging“
-Rückblick
-Ziel
Ziel des Krigings:
 Gewichtsoptimierung bei der Attributbestimmung
eines Punktes, der nicht beobachtet wurde.
II. Signalbehandlung
-statistische
Grundbegriffe
 Genauigkeit des geschätzten Attributwertes
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
Motivationsbeispiel:
Es wird die Ozonbelastung einer Region bestimmt:
Ist die aus den Punktdaten prädizierte Fläche jetzt
genau genug, um in Bereichen mit kritischen
Ozonwerten noch in die Sonne zu gehen.
Mathias Pennekamp ~ Kriging
7
II. Das Signal
I. Kriging – Einstieg
-Der Name
:“Kriging“
-Rückblick
-Ziel
II. Signalbehandlung
Statistik:
Deterministisches Modell:
bzw.
l + v = f(x) oder l = f(x) + v
l + v = Ax
-statistische
Grundbegriffe
-Semivarianz
-Semivariogramm
Approximation [Annäherung] der Beobachtung [ l ] durch eine
Funktion unter Minimierung der Verbesserungen [ v ].
III. Kriging
-Analysen im
Semivariogramm
Neu:
-Beispielrechnung
-verschiedene
Krigingverfahren
Stochastisches Signal:
Formel:
s
v
l = f(x) + s + n
Die Verbesserungen [v] werden in ein lokales Signal [s] und
ein normalverteiltes Rauschen [n] aufgespaltet.
Mathias Pennekamp ~ Kriging
8
Abb. 1
Geostatistik-Modell
Quelle:
Prof. Dr. W.-D. Schuh
Der Attributwert einer Zufallsvariablen wird mit z bezeichnet:
z(x) = f (x) + s + n
Unterschied von z(x) und l:
l
... Beobachtung
z(x) ... Attributwert auch für unbeprobte Stellen
Mathias Pennekamp ~ Kriging
9
I. Kriging – Einstieg
-Der Name
:“Kriging“
II. Signalbehandlung - statistische Grundbegriffe
l = f(x) +s + n
-Rückblick
-Ziel
II. Signalbehandlung
-statistische
Grundbegriffe
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
Der Erwartungswert [ E ]:
 Der Erwartungswert der Summe aller Signale über das
Gebiet ist null
 E { s } = 0 vgl. E {  v } = 0
 Lokal jedoch existiert ein Erwartungswert für das Signal
 E { s i } = si
E { si } = si
E { s } = 0
Mathias Pennekamp ~ Kriging
10
I. Kriging – Einstieg
II. Signalbehandlung - statistische Grundbegriffe
-Der Name
:“Kriging“
l = f(x) +s + n
-Rückblick
-Ziel
II. Signalbehandlung
-statistische
Grundbegriffe
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
Lokale Betrachtung des Signals:
 Idee 1: Die Beobachtungen l benachbarter Punkte sind ähnlich

Korrelationen (Abhängigkeit) zwischen den
benachbarten Punkten Pi(xi,yi)
 Idee 2: Je größer der Punktabstand, desto geringer die
Ähnlichkeit der Beobachtungen  Distanzabhängigkeit
-Beispielrechnung
-verschiedene
Krigingverfahren
P5
P1
P2
P6
P3
P4
Mathias Pennekamp ~ Kriging
11
I. Kriging – Einstieg
-Der Name
:“Kriging“
II. Signalbehandlung - statistische Grundbegriffe
l = f(x) +s + n
-Rückblick
-Ziel
Stationarität:
II. Signalbehandlung
-statistische
Grundbegriffe
-Semivarianz
 Idee 3: Die Lage der Punkte spielt für die Korrelation keine
Rolle, es interessiert nur die Distanz  Stationarität
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
z3
z1
P1
-Beispielrechnung
d12
P3
z2
P2
-verschiedene
Krigingverfahren
z4
d34
P4
In Pi wird zi beobachtet:
Stationarität heißt, wenn d12 = d34  E{ z12 } = E{ z34 }
und ist eine Voraussetzung für Kriging
Mathias Pennekamp ~ Kriging
12
I. Kriging – Einstieg
Verknüpfung von Distanz und Signal (1)
-Der Name
:“Kriging“
-Rückblick
-Ziel
II. Signalbehandlung
-statistische
Grundbegriffe
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
- Semivarianz -
Definition: (d) = ½{ z(P) – z(P+d) } ²
(d)
... Semivarianz für die Distanz d
z(P)
... Attributwert im Punkt P(x,y)
z(P+d) ... Attributwert in einem Punkt, der um d von
P(x,y) entfernt ist
Problem:
Vereinfachung:
Die Semivarianz muss für alle
Punkte des Datensatzes und für alle
Distanzen bestimmt werden.
Bildung von Entfernungsklassen:
Bsp.:
0 ... 40km
 [Komplexität] = O(n²) ;
40 ... 80km
 n ... Anzahl der Punkte
80 ...
Mathias Pennekamp ~ Kriging
13
I. Kriging – Einstieg
Verknüpfung von Distanz und Signal (2)
-Der Name
:“Kriging“
-Rückblick
-Ziel
II. Signalbehandlung
-statistische
Grundbegriffe
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
- Entfernungsklassen (Bsp.) -
1. Einordnen der Distanzen zwischen den
Punkten in die zugehörige Klasse
42, 44, 49, 51, 57, 67, 71  40 - 80
2. Berechnung des arithmetischen Mittels von
allen Distanzen in einer Klasse
54,43
3. Bestimmung der Semivarianzen zwischen
allen Punkten in der Klasse
6+5+4+3+2+1 = 21 Semivarianzen
4. Berechnung der mittleren Semivarianz einer
Entfernungsklasse
 eine Semivarianz pro Entfernungsklasse
Mathias Pennekamp ~ Kriging
14
I. Kriging – Einstieg
Verknüpfung von Distanz und Signal (3)
-Der Name
:“Kriging“
-Rückblick
-Ziel
II. Signalbehandlung
-statistische
Grundbegriffe
- Semivariogramm -
Ein Semivariogramm ist ein Diagramm, bei dem
Semivarianz und Distanz gegeneinander aufgetragen
wird.
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
z1
(d)
P1
 (d12)
z2
d12
-Beispielrechnung
-verschiedene
Krigingverfahren
P2
d12
d
 (d12) = ½ { z1 – z2 } ²
Mathias Pennekamp ~ Kriging
15
Empirisches Semivariogramm
I. Kriging – Einstieg
-Der Name
:“Kriging“
-Rückblick
Problem (u.a.):
(d)
- ...
-Ziel
II. Signalbehandlung
-statistische
Grundbegriffe
?
- nur punkthafte
Information
-Semivarianz
d
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
Lösung (u.a.): Theoretisches Semivariogramm
- Approximation der
Punkte durch eine
Funktion
d
Mathias Pennekamp ~ Kriging
16
III. Kriging
I. Kriging – Einstieg
-Der Name
:“Kriging“
-Rückblick
-Ziel
II. Signalbehandlung
Idee:
Optimierung der Gewichte mit Hilfe des
Semivariogramms
Vorteil: Genauigkeit der geschätzten Fläche ist
bestimmbar.
-statistische
Grundbegriffe
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
Größen des Semivariogramms sind Nugget, Range
und Sill.
Mathias Pennekamp ~ Kriging
17
Analysen im
Semivariogramm
I. Kriging – Einstieg
-Der Name
:“Kriging“
-Rückblick
-Ziel
II. Signalbehandlung
-statistische
Grundbegriffe
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
• Nugget ist ein Maß für Streuung des Signals im Nahbereich
(Messfehler):
Semivarianz für d = 0: (d) = ½{ z(P) – z(P+d) } ²  (d) = 0
• Range gibt an, wie weit die Punkte korrelieren:
Bestimmung der Größe der Nachbarschaft, dessen Punkte ich zur
Interpolation verwende.
• Sill gibt das Maximum des Semivariogramms an. Sie ist ein Maß
für die Varianz der beobachteten Attributwerte.
Mathias Pennekamp ~ Kriging
18
I. Kriging – Einstieg
-Der Name
:“Kriging“
-Rückblick
-Ziel
Beispiel zur Bestimmung der optimalen Gewichte:
• geg.: Punktdatensatz
• ges.: Attributwert an einem unbeprobten Ort
II. Signalbehandlung
-statistische
Grundbegriffe
-Semivarianz
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
1) Bestimmung der Distanzen
zwischen den Punkten
2) Bestimmung der Semivarianzen
für alle Distanzen [ij]
?
Range
3) Aufstellen einer Matrix, die diese
Semivarianzen enthält
4) Bestimmung der optimalen
Gewichte mit dem KrigingSchätzer
Zu 1) Im Normalfall  Entfernungsklassen berücksichtigen
Zu 2) Semivarianzen aus dem Semivariogramm bestimmen
Mathias Pennekamp ~ Kriging
19
I. Kriging – Einstieg
-Der Name
:“Kriging“
-Rückblick
-Ziel
II. Signalbehandlung
-statistische
Grundbegriffe
-Semivarianz
Zu 3) Matrix der Semivarianzen
11 . . .16
:
:
61 . . .66
1 ...1
1
1
10
:
:
:
1 * 6 = 60
0
m
1
-Semivariogramm
III. Kriging
-Analysen im
Semivariogramm
Semivarianz für die Punkte
1 und 6
5
6
?
0
-Beispielrechnung
-verschiedene
Krigingverfahren
4
Zu 4) Die zu berechnenden, optimalen
Gewichte sind 1- 6 .:
1
2
3
Lösung: z0 = 1*l1 + 2*l2 + ... + 6*l6
Warum ?  Ausarbeitung
Mathias Pennekamp ~ Kriging
20
I. Kriging – Einstieg
Verschiedene Krigingverfahren
-Der Name
:“Kriging“
1. Verfahren mit unterschiedlicher Trendelimination
-Rückblick
1.1 Simple Kriging
-Ziel
II. Signalbehandlung
1.2 Ordinary Kriging
-statistische
Grundbegriffe
1.3 Universal Kriging
-Semivarianz
2. Indicator Kriging
-Semivariogramm
3. Probability Kriging
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
4. Disjunctive Kriging
1.1 Simple Kriging
Der Trend f(x) wird beim Simple
Kriging konstant gesetzt, d.h. man setzt
den globalen Mittelwert als Trend ein:
f (x) = 

5. Co-Kriging
s
l
Mathias Pennekamp ~ Kriging
21
I. Kriging – Einstieg
Verschiedene Krigingverfahren
-Der Name
:“Kriging“
1. Verfahren mit unterschiedlicher Trendelimination
-Rückblick
1.1 Simple Kriging
-Ziel
II. Signalbehandlung
1.2 Ordinary Kriging
-statistische
Grundbegriffe
1.3 Universal Kriging
-Semivarianz
2. Indicator Kriging
-Semivariogramm
3. Probability Kriging
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
1.2 Ordinary Kriging
Der Trend f(x) wird beim Ordinary
Kriging durch eine Funktion (z.B.
Polynom 3. Grades) global approximiert
und vorm Kriging eliminiert.
4. Disjunctive Kriging
5. Co-Kriging
-verschiedene
Krigingverfahren
l
Mathias Pennekamp ~ Kriging
22
I. Kriging – Einstieg
Verschiedene Krigingverfahren
-Der Name
:“Kriging“
1. Verfahren mit unterschiedlicher Trendelimination
-Rückblick
1.1 Simple Kriging
-Ziel
II. Signalbehandlung
1.2 Ordinary Kriging
-statistische
Grundbegriffe
1.3 Universal Kriging
-Semivarianz
2. Indicator Kriging
-Semivariogramm
3. Probability Kriging
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
1.3 Universal Kriging
Der Trend f(x) wird wie beim Ordinary
Kriging eliminiert, mit dem Unterschied,
dass lokale Trends (Signal)
berücksichtigt werden können. Möglichkeit der iterativen Trendbestimmung:
4. Disjunctive Kriging
5. Co-Kriging
-Parameterschätzung
-verbleibendes Signal
liefert Abhängigkeiten
l
-Iterationsprozess
möglich mit neuen
Parametern
Mathias Pennekamp ~ Kriging
23
I. Kriging – Einstieg
Verschiedene Krigingverfahren
-Der Name
:“Kriging“
1. Verfahren mit unterschiedlicher Trendelimination
-Rückblick
1.1 Simple Kriging
-Ziel
II. Signalbehandlung
1.2 Ordinary Kriging
-statistische
Grundbegriffe
1.3 Universal Kriging
-Semivarianz
2. Indicator Kriging
-Semivariogramm
3. Probability Kriging
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
2. Indicator Kriging
Entwirft eine Karte, die angibt mit
welcher Wahrscheinlichkeit ein wählbarer Schwellenwert (Threshold), wie
z.B. ein kritischer Ozonwert erreicht
wird.
4. Disjunctive Kriging
5. Co-Kriging
-verschiedene
Krigingverfahren
l
Mathias Pennekamp ~ Kriging
24
Verschiedene Krigingverfahren
I. Kriging – Einstieg
-Der Name
:“Kriging“
1. Verfahren mit unterschiedlicher Trendelimination
-Rückblick
1.1 Simple Kriging
-Ziel
II. Signalbehandlung
1.2 Ordinary Kriging
-statistische
Grundbegriffe
1.3 Universal Kriging
-Semivarianz
2. Indicator Kriging
-Semivariogramm
3. Probability Kriging
III. Kriging
-Analysen im
Semivariogramm
-Beispielrechnung
-verschiedene
Krigingverfahren
5. Co-Kriging
Co-Kriging benutzt zur Interpolation der
Fläche einen zweiten Datensatz eines
Attributs (z.B. Cd-Belastung), welches
sich ähnlich zum ersten Datensatz (z.B.
Pb-Belastung) verhält.
4. Disjunctive Kriging
5. Co-Kriging
Vorteil:
Schwach beprobte Stellen
können effizienter
geschätzt werden.
l
[Multivariates Kriging]
Mathias Pennekamp ~ Kriging
25