Materialeigenschaften: Dielektrika
Werbung

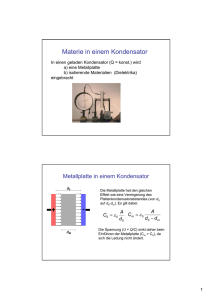
Materialeigenschaften: Dielektrika Antwort auf ein elektrisches Feld Inhalt • Definition der Dielektrizitätszahl • Materialeigenschaften, makroskopisch und auf atomarer Skala: – Verschiebungspolarisation – Orientierungspolarisation • • • • • Dielektrika Parelektrika Ferroelektrika Pyroelektrika Piezoelektrika Die Dielektrizitätszahl • Ein elektrisches Feld verschiebt die Ladungsschwerpunkte in der Materie (Polarisation) • Die getrennten Ladungen verursachen ein Gegenfeld • Zwischen den Platten eines Kondensators fällt deshalb die Spannung bei konstanter Ladung: Die Kapazität wird größer Die Spannung als Funktion der Feldstärke 1 0 Volt 0,5 Q UV d EV Die Spannung als Funktion der Feldstärke mit Dielektrikum 1 0 Volt 0,5 Q Durch Polarisation erzeugtes Gegenfeld U d ( EV EP ) Die Spannung als Funktion der Ladung 1 0 Volt 0,5 Q UV C Q Definition der Dielektriziätszahl εr C r CV C , CV r 1F 1F 1 Definition der Dielektrizitätszahl oder Permittivitätszahl Kapazitäten eines Kondensators mit und ohne Dielektrikum Dielektrizitätszahl des Mediums Kleinere Spannung bei gleicher Ladung Q C U Ladung und Spannung im 1 F Kondensator mit Dielektrikum Q CV UV Ladung und Spannung 1F Kondensator im Vakuum C Uv r CV U U 1 r Uv 1 Definition der Dielektriziätszahl 1 Bei konstanter Ladung ist die Spannung mit Dielektrikum um den Faktor 1/εr kleiner Kleinere Feldstärke im Kondensator mit Dielektrikum U v Ev d r U E d E 1 r EV 1 V/m Spannungen und Feldstärken 1 V/m Die effektive Feldstärke fällt um den Faktor 1/εr Versuch • Ein Kondensator wird statisch aufgeladen und dessen Spannung mit einem Elektrometer überprüft. • Wird ein Dielektrikum eingebracht, dann sinkt die Spannung, wegen steigt also die Kapazität C. Bei entfernen des Dielektrikums steigt sie auf ihren ursprünglichen Wert. Spannung mit und ohne Dielektrikum Kondensator in Luft Q U C vak Kondensator mit Dielektrikum 1 Q U r Cvak Weitere, aus der Dielektrizitätszahl abgeleitete Größen r 0 0 8,854 10 12 1 F/m Die Permittivität 1 F/m Feldkonstante, deshalb auch „Permittivität des Vakuums“ genannt r 1 Dielektrizitätszahl r 1 1 Die Suszeptibilität Polarisation auf atomarer Skala Im Material erscheinen Dipole, Grund: • Verschiebungspolarisation – Ursache für Dielektrizität, in allen Materialien vorhanden • Orientierungspolarisation – – – – Erscheint in Parelektrischen Materialien Voraussetzung: Polare Moleküle Im elektrischen Feld werden sie ausgerichtet Die thermische Bewegung verhindert vollständige Ausrichtung • Häufigkeit der Orientierung entsprechend dem Boltzmannfaktor • Ferroelektrizität: kollektive Polarisation im Gitter Dipole in Materie Verschiebungspolarisation • Die Schwerpunkte der Ladungen verschieben sich im äußeren Feld – Neutrale Atome werden zu Dipolen • Temperatur unabhängig • Schnell, in Phase mit der Anregung, folgt den Lichtwellen und verursacht den Brechungsindex (Ausnahme: Resonanzen), – Die Strahlung der angeregten Dipole ist Ursache der „kohärentenStreuung“ • Schwacher Effekt, ist aber immer vorhanden • Keine Sättigung, wächst mit der Feldstärke Verschiebungspolarisation Atom mit Kern und negativer Elektronenwolke Verschiebungspolarisation Feldrichtung Molekularer Dipol Orientierungspolarisation: Parelektrische Stoffe • Auf vorhandene Dipole wirkt ein Drehmoment im äußeren Feld – Dipole drehen sich in Feldrichtung • Temperaturbewegung stört die Ausrichtung • Hinkt dem Feld nach, je mehr, je höher viskos das Medium ist • Sättigung ist erreicht, wenn alle Dipole ausgerichtet sind Orientierungspolarisation Dipol, z. B. Wasser Orientierungspolarisation Dipol, z. B. Wasser, Schwerpunkte der positiven und negativen Ladung Elektrische Dipole p Q l E l F QE T p E Ql E Elektrisches Dipolmoment, Ladung ±Q Vektor l Im homogenen elektrischen Feld wirkt auf einen elektrischen Dipol ein Drehmoment Verknüpfung zwischen Dielektrizitätszahl ε und mikroskopischer Polarisierbarkeit p Polarisierbarkeit Geringe Dichte, z. B. Gase: Jedes Teilchen „sieht“ die Vakuumfeldstärke p EV Hohe Dichte, Teilchen sehen die effektive Feldstärke p E Mikroskopische Polarisierbarkeit und Dielektrizitätszahl ( 1) M Mol 1 0 NA ( 1) M Mol 1 NA ( 2) 3 0 1 10 Versuch • Kraft auf einen Wasserstrahl. Ein statisch geladener Stab induziert Dipole im Wasser, diese streben zum geladenen Stab. Versuch • Kraft auf Luftblasen in Öl. Eine in einem Ölbad befindliche Spitze wird aufgeladen. Im Öl entstehen Dipole, die zur Spitze streben. Die Luftblasen stören dabei, sie werden von der Spitze weg gedrängt. Parelektrische Materialien Polarisierbarkeit Curie Gesetz für die Suszeptibilität 1 p~ E T n( Sättigung p 2 3kT ) P E 10 100 Ferroelektrika • Ferroelektrika sind kristalline Materialien • Unterhalb der „Curie Temperatur“ erscheinen permanente Dipole • Im elektrischen Feld bewirkt die Wechselwirkung zwischen den Gitterplätzen eine kollektive Ausrichtung – Sehr hohe Dielektrizitätszahl Polarisation in Ferroelektrika Beispiel: Einheitszelle eines BaTiO3 Kristalls. Unterhalb Tc, der Curie Temperatur, verschiebt sich der Schwerpunkt der negativen gegenüber der positiven Ladung Ferroelektrische Materialien Die Polarisierbarkeit zeigt eine Hysterese Dielektrizitätszahl P E Hysterese 10 10 3 5 Versuch • Hysterese am BaTiO3 Piezoelektrische Materialien • Kristalline Materialien, Coulombkräfte zwischen polaren Baugruppen sind im Gleichgewicht mit elastischen Kräften • Mechanischer Druck ändert die Länge des Bauteils und stört das Gleichgewicht: Es erscheinen Ladungen an den Oberflächen • Umkehrung des Effekts: Ein elektrisches Feld ändert die Längen • Anwendung: Elektro-mechanische Aktoren Versuch • Spannung am Seignette-Salz bei zunehmendem Druck Pyroelektrische Materialien • Analog zu den piezoelektrischen Materialien, anstelle des mechanischen Drucks steht die Temperatur: • Die Temperatur ändert die Länge des Bauteils und stört das Gleichgewicht: Es erscheinen Ladungen an den Oberflächen Schema eines piezoelektrischen Kristalls Zusammenfassung Definition der Dielektrizitätszahl εr : Quotient, • Zähler: Kapazität mit Material • Nenner: Kapazität ohne Material Eigenschaften der Materialien in allen Aggregatzuständen: • Dielektrika: Dipole entstehen im Feld, 1< εr <10 • Parelektrika: Vorhandene Dipole werden im Feld ausgerichtet, 10< εr <100 Nur in Kristallen: • Ferroelektrika, Ausrichtung großer polarer Bereiche, 103 < εr <105 • Pyroelektrika: Dipole entstehen bei Erwärmung • Piezoelektrika: Dipole entstehen bei Druck – Anwendung: Elektromechanische Aktoren Aggregatzustand, Ladungsträger und Leitfähigkeit Gas Flüssig Elektronen Ionen Elektrolytische Leitung Spontaner Durchbuch, z. B. Blitz Fest Elektronen Halbleiter: Nicht Ohmscher Stromfluss Metall Isolator In Grenzen: Nur nach Aktivierung: Ohmsche Leitung, U=R.I