GDI Kapitel 3 Uebung 2007-05

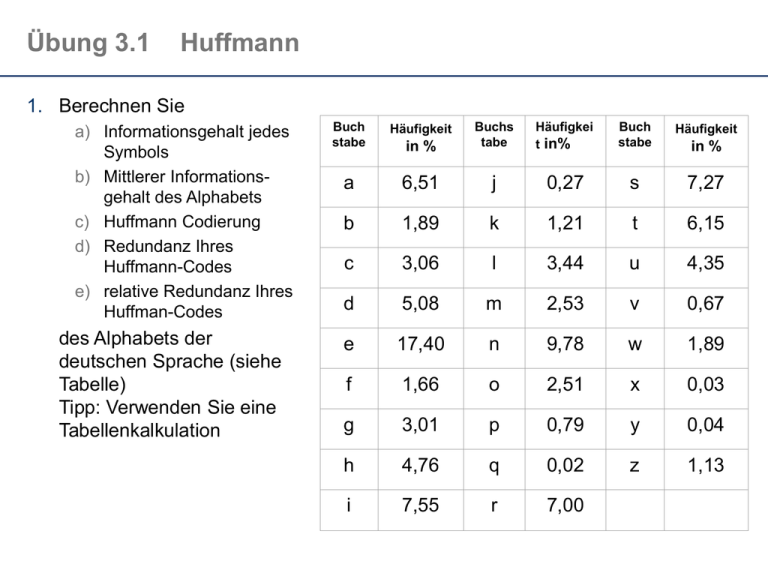
Übung 3.1
Huffmann
1. Berechnen Sie
a) Informationsgehalt jedes
Symbols
b) Mittlerer Informationsgehalt des Alphabets
c) Huffmann Codierung
d) Redundanz Ihres
Huffmann-Codes
e) relative Redundanz Ihres
Huffman-Codes
des Alphabets der
deutschen Sprache (siehe
Tabelle)
Tipp: Verwenden Sie eine
Tabellenkalkulation
Buch
stabe
Häufigkeit
Häufigkei
t in%
Buch
stabe
Häufigkeit
in %
Buchs
tabe
a
6,51
j
0,27
s
7,27
b
1,89
k
1,21
t
6,15
c
3,06
l
3,44
u
4,35
d
5,08
m
2,53
v
0,67
e
17,40
n
9,78
w
1,89
f
1,66
o
2,51
x
0,03
g
3,01
p
0,79
y
0,04
h
4,76
q
0,02
z
1,13
i
7,55
r
7,00
in %
Übung 3.2
Hamming
1. Gegeben ist folgende Codierung:
Code(a) = 10001000; Code(b) = 10111011; Code(c) = 10001111
a)
b)
c)
d)
Wie groß ist der Hammingabstand zwischen den einzelnen Codeworten ?
Wie groß ist der Hamming-Abstand D des (gesamten) Codes ?
Wieviele Bitfehler sind damit erkennbar ? Wieviele korrigierbar ?
Geben Sie ein (ungültiges) Codewort an, welches korrigiert werden kann, obwohl
((D-1)/2)+1 bits fehlerhaft sind. Begründen Sie Ihre Antwort.
2. Codieren Sie alle 4bit-Worte (also 0000-1111) nach Hamming.
3. Betrachten Sie den mit der Hamming-Methode codierten Code für „1000“
a) Kippen sie jedes Bit je einmal und bestimmen sie das gekippte Bit mit der HammingMethode.
b) Was passiert, wenn zwei Bits gekippt sind - verdeutlichen Sie dies anhand eines
Beispiels.
4. Gegeben ist folgendes Wort: 1010101010
a) Wieviele Parity-Bits brauchen Sie nach der Hamming-Methode für dieses Wort
b) Wieviele unterschiedliche Worte könnte man mit dieser Anzahl von Parity-Bits nach
Hamming codieren ?
c) Codieren Sie dieses Wort nach der Hamming-Methode