Die kosmische Entfernungsleiter Vermessung des Weltraums
Werbung

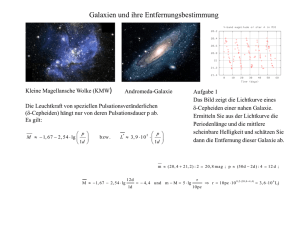
Seminar Astro­ und Teilchenphysik Die kosmische Entfernungsleiter ­ Vermessung des Weltraums Patrick Levi, 15.12.2003 GLIEDERUNG 1. Grundlagen 2. Absolute Abstandsmessmethoden 3. Relative Abstandsmessmethoden 4. Ergebnisse Grundlegendes Sternphotometrie – wichtige Zusammenhänge Ein Stern emittiere an seiner Oberfläche den Strahlungsstrom Fλ . Seine Entfernung sei r, sein Radius R. So erreicht uns auf der Erde der Strahlungsstrom Die Leuchtkraft L ist gegeben durch Grundlegendes Sternphotometrie Was man von einem Stern gut beobachten kann ist seine Helligkeit, den Lichtfluss von seiner Oberfläche, der uns auf der Erde erreicht. Man definiert die relativen Helligkeiten in Einheiten von Magnitudines folgendermaßen, wenn f1 und f2 die Strahlungsströme zweier Sterne sind: Grundlegendes Sternphotometrie Die scheinbare Helligkeit m eines Sternes hängt von seiner wahren Helligkeit und vom Abstand ab. Daher definiert man die absolute Helligkeit M in Bezug auf einen „Normabstand“ von 10 pc. Es ergibt sich folgender Zusammenhang Interessiert man sich für die Gesamtstrahlung und nicht nur für Absolute Messmethoden – Übersicht Trigonometrische Parallaxe Statistische Parallaxe Bewegung von Clustern Baade­Wesselink­Methode Sunyaev­Zel' dovich­Effekt Zeitverschiebungen Zeitverschiebungen und Gravitationslinsen Trigonometrische Parallaxe Aufgrund der Rotation der Erde um die Sonne erscheint es für einen Beobachter auf der Erde, als würde ein Stern am Himmel eine elliptische Bahn zurücklegen. Der Winkel gegenüber der großen Halbachse heißt Parallaxe p. Trigonometrische Parallaxe Über trigonometrische Beziehungen erhält man p=1' ' entspricht einer Entfernung von 3,26 ly = 3,086 x 1016 m = 1 pc Messbare Entfernungen: 500 pc bis 1000 pc Genauigkeit der Messungen: 0,01' ' (photografisch) 0,001' ' / 0,002' ' (Präzissionsmessungen) Baade – Wesselink ­ Methode Gesamtstrahlungsstrom an der Sternoberfläche (Planck) C ist bekannte Konstante R ist der Sternradius (Problem: Messung!!) Lösung: variable Sterne – Dopplerverschiebungen im Spektrum variieren mit der selben Periode wie seine Helligkeit Baade – Wesselink ­ Methode Cepheiden Sterne hoher Leuchtkraft Perioden von ca. 1 d bis 50 d treten v.a. in den Spiralarmen der Milchstraße auf RR Lyrae Sterne Perioden von ca. 0,2 d bis 1,2 d treten v.a. im Halo und Kern der Milchstraße auf Baade – Wesselink ­ Methode Grund für diese Schwankungen: Atmosphäre instabil, führt zu Größernänderung des Sterns ∆r1 „line­of­sight“­ Geschwindigkeit der Atmosphäre (Vorzeichen!) Messung: Dopplerverschiebung Faktor p: Ausdehnung nicht nur in der „line of sight“ Baade – Wesselink ­ Methode Es ergibt sich damit eine Änderung der Magnitudes zwischen zwei Radien Gelingt Messung von Teff und der Magnitudenänderung im Zeitintervall, so erhält man r0 und damit den Abstand. Baade – Wesselink ­ Methode Fehlerquellen Messfehler bei der Bestimmung von r0 (z.B. Zusammenhang Farbe – Temperatur) Fehler im Modell: ➢ verschiedene Regionen der Atmosphäre expandieren mit versch. Geschwindigkeiten ➢ nicht unbedingt radiale Ausdehnung Lösung: Entwicklung besserer Modelle Sunyaev – Zel' dovich Effekt (SZ­Effekt) Kosmische Hintergrundstrahlung entstand kurz nach den Big Bang. Die meisten dieser Photonen seither ohne WW. einheitliche Mikrowellenstrahlung aus allen Richtungen Ein geringer Bruchteil wechselwirkte mit anderen Objekten im All. Photonen durch Galaxien­Cluster: WW mit Elektronen (Compton­Streuung) in heißem Gas Energieerhöhung der Photonen Verschiebung nach höheren Frequenzen Es ergibt sich eine Verzerrung des Hintergrundspektrums Sunyaev – Zel' dovich Effekt Größe der Verzerrung hängt von der Streuwahrscheinlichkeit PSZ ab: optische Tiefe für Streuung wenn ein Photon entlang dem Weg S durch einen Cluster mit Elektronendichte ne läuft. Thomsonscher Wirkungsquerschnitt Sunyaev – Zel' dovich Effekt Elektronen streuen mit Protonen im heißen Plasma (Temperatur TX) Röntgen­Bremsstrahlung Der Röntgen­Strahlungsfluss der von einem Cluster ausgeht, hängt von TX, ne und dem Abstand r ab. TX aus obiger Gleichung (Emissivität) ne aus SZ­Effekt Methode zur Bestimmung des Abstandes Sunyaev – Zel' dovich Effekt Methode zur Messung außergalaktischer Entfernungen. Vorteile: ● beruht auf direkten Beobachtungen physikalische Modelle verstanden Nachteile: •Strahlungsemission in Cluster von der Position innerhalb dessen abhängig! Abstandsmessung mittels Zeitverschiebungen Ist die Lichtemission eines astrophysikalischen Objekts zeitabhängig, so kann dadurch eine Abstandsmessung ermöglicht werden. Beispiel: Der Ring um Supernova 1987 A Abstandsmessung mittels Zeitverschiebungen scharfe Emissionslinien von hoch­ionieiserten Atomen im Spektrum von SN 1987A festgestellt, die nur ca. 90 d nach der Explosion entdeckt wurden und ein Maximum nach ca. 400 d annahmen. Erklärung: Absorption und Wiederabstrahlung an Material um die SN herum. Daraus lässt sich der Abstand wie folgt berechnen Zeitverzögerung zwischen B und A Zeitverzögerung zwischen A und C Relativ­Abstände – Übersicht Leuchtkraft variabler Sterne (Cepheiden) Leuchtkraft planetarischer Nebel Leuchtkraft von Kugelsternhaufen Novae / Supernovae Tully­Fisher (Spiralgalaxien) Faber­Jackson (Elliptische Galaxien) Fluktuationen der Oberflächenhelligkeit Messung von Relativ­Abständen Bei der Messung von Abständen zu astrophysikalischen Objekten haben wir bisher einfach modellierbare Prozesse und Geometrien ausgenutzt. Aber: Die meisten Objekte sind nicht so einfach modellierbar. Jedoch lassen sich einfache Zusammenhänge zwischen Eigenschaften der Objekte herstellen, die nach entsprechender Kalibration eine Messmethode für den relativen Abstand liefern. Messung von Relativ­Abständen Prinzip der Relativ­Abstand­Messung Messe eine abstandsunabhängige Eigenschaft der Objekte (z.B. Farbe) Messe eine abstandsabhängige Eigenschaft (Helligkeiten) Kombiniere beide Messungen Abstand Kalibrieren: Für mindestens ein Beispiel eines Systems muss eine unabhängige Abstandsmessung durchgeführt werden. Messung von Relativ­Abständen Vorteile basieren nur auf (empirisch kalibirerten) Beobachtungen, keine Annahmen oder Modelle funktionieren mit gewöhnlichen Quellen man kann sehr große Abstände messen. Nachteil keine Evolution angenommen „ Standard candles“ und Cepheiden Um solche Messungen zu kalibrieren sucht man nach Objekten mit universell gültigen Leuchtkraft­Funktionen („standard candles“). Cepheiden als standard candles: Cepheiden eignen sich besonders gut als standard candles: 1. sie sind hell sind, also auch in größeren Abständen sichtbar 2. ihre Veränderlichkeit charakterisiert sie 3. in der Milchstraße vorhanden zwecks Kalibrierung 4. sie erfüllen wohl­definierte Relationen Cepheiden als standard candles Für einen Cepheiden der Periode P gilt für die absolute Helligkeit Planetarische Nebel als standard candles Planetarische Nebel gut zu detektieren, da Emission in Linien aus der Gesamtemission einer Galaxie herausfilterbar kommen in allen Typen von Galaxien in großer Anzahl vor Planetarische Nebel als standard candles NGC 7293 Planetarische Nebel als standard candles Messungen im Bereich 500,7 nm zeigen, dass sich in diesem Bereich die Leuchtkraft Funktion exponentiell verhält (PNLF) ist die maximale Magnitude planetarischer Nebel PNLF ist universell, cut­off unverwechselbares Merkmal der Funktion gut als standard candle geeignet Planetarische Nebel als standard candles M31 Aus der Differenz der Werte für mcut erhält man Relativabstand Novae und Supernovae Novae: sind sehr hell auch in entfernten Galaxien beobachtbar tauchen sowohl in elliptischen als auch in Spiral­Galaxien auf Man kann den Abstand direkt messen, indem man den Durch­ messer bestimmt (Parallaxe). Bei extragalaktischen Novae ist dieser aber nicht messbar. aber: Die Maximalhelligkeit eignet sich nicht als standard candle, da die Maximalhelligkeit um bis zu 4 Magnitudines variiert, je nach Stadium! Novae und Supernovae Abstandsmessungen mittels Novae: Aus Beobachtungen von 11 Novae in der Milchstraße fand man folgende Beziehung t2 ist die Zeit welche die Nova braucht um von MV (max) 2 Magnitudines abzunehmen. Novae und Supernovae Novae und Supernovae Genauigkeit: ca. 25% Aber: Es wurden Novae beobachtet, die von diesem Verhalten abweichen (M31). Diese abweichenden Novae sind leuchtstärker als die „normalen“, daher bei großen Entfernungen nicht leicht zu extrahieren! Novae und Supernovae Typ Ia Supernovae: Supernovae entstehen wahrscheinlich alle von im Prinzip identischen Systemen Ähnlichkeiten, auch in der Leuchtkraft man erhält sehr leuchtstarke standard candles Kalibrierung via bekannter Abstände zu den Systemen, die Supernovae enthalten. Konsistent mit Modellierung der Explosion und Fit unbekannter Parameter. Aber: Auch Zweifel an der Eignung als standard candles, da Abweichungen beobachtet. Galaxien – Kinematische Betrachtungen Grundlegendes: Galaxien sind nicht als standard candles verwendbar! Unterscheiden: Elliptische und Spiralgalaxien Kinematische Betrachtungen Spiralgalaxien Es ist möglich die Masse einer Galaxie bis zu einem bestimmten Radius R zu erfassen. Für eine kugelsymmetrische Massenverteilung ergibt sich für die Rotationsgeschwindigkeit V(R) wobei M(R) die Gesamtmasse innerhalb des Radiuses R bezeichnet. Tully – Fisher ­ Beziehung Bei weit entfernten Galaxien: Rotationskurven sind räumlich nicht mehr auflösbar. Beobachtung von Tully und Fisher: Die Dopplerbreite der 21 – cm – Linie gehorcht folgender Beziehung: (Tully – Fisher – Beziehung) Tully – Fisher – Beziehung Abstandsmessung mittels Tully – Fisher – Beziehung: Sei r die Entfernung zur beobachteten Galaxie, so gehorcht ihr Winkeldurckmesser α der Beziehung Damit Nun muss man eine Masse – Leuchtkraft – Beziehung zu Grunde legen. Aus Messungen naher Galaxien: M/L wächst mit Abstand zum Zentrum an. Kinematik Elliptischer Galaxien In einer elliptische Galaxien dominieren statistischen Bewegungen gegenüber großräumiger Rotationen. Maß für die statistischen Bewegungen ist das mittlere Geschwindigkeitsquadrat und die Streuung der Geschwindigkeit Benutzen Korrelationen in elliptischen Galaxien: (Faber – Jackson – Beziehung) Fluktuationen der Oberflächen­Helligkeit Modell: Eine Galaxie im Abstand D bestehe aus N gleichartigen Sternen mit n Sternen pro Oberflächeneinheit. L sei die Leuchtkraft eines Sterns. Eine Aufnahme der Galaxie mit Winkelauflösung δθ enthält Sterne pro Flächenelement Der beobachtete Fluss, der von jedem Stern ausgeht ist gegeben durch Fluktuationen der Oberflächen­Helligkeit Damit erhält man für den mittleren totalen Fluss pro Flächenelement Vom Modell zu Realität: Poisson­Verteilung der Sterne; die Anzahl der Sterne pro Oberflächenelement wird um fluktuieren. Daraus folgt für die Varianz Fluktuationen der Oberflächen­Helligkeit Tatsächlich bestehen Galaxien aus verschiedenen Sternarten, mit innerer Leuchtkraft Li. Es ergibt sich damit für f mit gewichteter mittlerer Leuchtkraft Fluktuationen der Oberflächen­Helligkeit Bestehen Galaxien aus der selben Zusammensetzung von Sternarten, so kann man aus der eben hergeleiteten Beziehung ihren relativen Abstand bestimmen, indem man f misst. Messung von <L> (oder Berechnung aus LKF): absoluter Abstand Kalibrierung der Messmethode (wenn Abstand bekannt) Ergebnisse Generell: Beim Aufstellen einer kosmischen Entfernungsleiter sind die systematischen Fehler zu beachten, die einigen Messmehtoden bzw. Kalibrationen inne wohnen!! Jedoch: Immer bessere Messmethoden sowie Vergleich von relativen und absoluten Abständen auf Konsistenz helfen, systematische Fehler zu minimieren. Je weniger Kalibrierungsschritte, umso genauer! Genauigkeit bis ca. 10% erreichbar. Ergebnisse Abstände innerhalb der Lokalen Gruppe Abstand zur Großen Magelanschen Wolke (LMC): Relative Methoden Cepheiden: 50±2 kpc RR Lyrae 44±2 kpc (Halo von LMC) Absolute Methoden unabhängige Messmethoden durch Supernova 1987a: Baade­Wesselink angewandt auf expandierende Photospäre: 55±5 kpc Zeitverschiebungen: 52±3 kpc Im Großen und Ganzen Übereinstimmung der verschiedenen Methoden! Also ist es wahrscheinlich dass keine der Methoden stark fehlerbehaftet ist. Abstände innerhalb der Lokalen Gruppe Abstand zu M31 (Andromeda Galaxie): Nächste große Spiralgalaxie wichtig für Kalibrierungen Beobachtungen von Cepeiden: Beziehung zw. absoluten Magnitudines und Periode festlegen: Problem hierbei: Nullpunktsfestlegung Relativabstandsmessungen zu LMC Vergleich von Cepheiden der beiden Systeme: 760±50 kpc Vergleich von RR Lyrae 750±50 kpc PNLF: 750±50 kpc Abstände innerhalb der Lokalen Gruppe M31 Novae: 710±80 kpc Beste Schätzung: 740±40 kpc Fazit: Konsistenz der verschiedenen Methoden der am genauesten bestimmte Abstand zu einer ausgedehnten Galaxie. Wichtig für Kalibrierung (z.B. PNLF und GCLF) !! Über die Lokale Gruppe hinaus Über die Lokale Gruppe hinaus Abstand zum Virgo­Cluster: VC ist der nächste mittelgroße Galaxien­Cluster Enthält sowohl Spiral­ als auch elliptische Galaxien in großer Anzahl, damit auch Supervonae Einmal Abstand bestimmt kann man mit VC bestimmen, welche Eigenschaften ein vermutlich „durchschnittlicher“ Cluster hat. Kalibrierung für Abstandsmessungen entfernterer Cluster. Über die Lokale Gruppe hinaus Virgo Cluster 20 Cepheiden in Galaxie M100: 17,1±1,8 Mpc, konsistent, da VC mehrere Mpc ausgedehnt! Beachte: Diese Methode benötigt weniger Kalibrierungsschritte! wahrscheinlicheres Ergebnis Abstände mittels Methoden geringster Ungenauigkeit (Fluktuationen d. Oberflächenhelligkeit, PNLF, Tully­Fisher): 16±1 Mpc 10 Typ Ia Supernovae: 23±2 Mpc!! Bestätigt Zweifel an SN Ia als standard candles (wird z. Zt. untersucht)! Hubble Gesetz Hubble Gesetz: Zusammenhang zwischen Abstand D und der Rotverschiebung ∆λ Jede Abweichung vom Hubble Gesetz kann Anzeichen für eine der Galaxie eigene Geschwindigkeit sein. Unabhängig von Kalibrierung! Da aber die besten Abstandsmessungen immernoch Fehler von ca. 10% haben, sind nur große Abweichungen vom Hubble Gesetz verwertbar. Hubble Gesetz Bestimmung der Hubble Konstanten mit Hilfe des Virgo­ Haufens: Rotverschiebung: Lokale Gruppe spürt Gravitation des Virgo Haufens (virgozentrische Einfall) in der Rotverschiebung nicht nur Einfluss der Expansion des Universums sichtbar. kosmische Fluchtgeschwindigkeit und Geschwindigkeit des virgozentrischen Einfalls bestimmt zu v=1175±30 km/s Folglich Hubble Gesetz Dieser Wert wird bestätigt durch die Bestimmung von H0 mittels Hubble­Diagramm (liefert auch Evidenz für lineare Ausdehnung). Hubble Gesetz Hat man eine standard canlde gegeben, so ist M nahezu konstant. Die Gleichung für H0 vereinfacht sich dann zu Blaue Supernovae Ia zeigen ein solches Verhalten. Man erhält dadruch einen Wert von 57±3 km/(s Mpc) Hubble Gesetz Literatur [1] J. Binney, M. Merrifield, Galactic Astronomy, Princeton University Press 1998 [2] A. Unsöld, B. Baschek, Der neue Kosmos, Springer 1999, 6. Auflage [3] L. Labhardt, M. Federspiel, A. Tammann, Der Wert der Hubble­Konstante, Sterne und Weltraum 5/98 [4] W.L. Freedman, Measuring Cosmological Parameters, Artikel