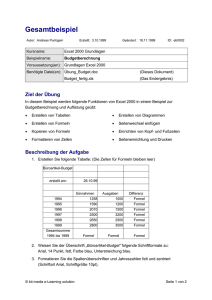
Kapitel 1 "Aussagenlogik"

Kapitel 1
Aussagenlogik
Die Aussagenlogik behandelt die möglichen Bezüge zwischen Aussagensätzen, also Sätzen, denen man sinnvollerweise die Wahrheitswerte „wahr“ oder „falsch“ zuordnen kann, in Hinblick auf
diese Wahrheitswerte. Wichtig ist bei einer formalen Logik dabei nicht, ob konkrete Sätze in einer konkreten Situation gelten oder nicht, oder ob ihre Gültigkeit oder Ungültigkeit nachgeprüft
werden kann, sondern allein die sinnvolle Möglichkeit der Zuordnung von Wahrheitswerten. Es
ist daher günstig, vom konkreten Inhalt der Sätze zu abstrahieren und diese durch eine symbolhafte Schreibweise wiederzugeben, ebenso wie die möglichen Bezüge der Sätze untereinander
durch besondere Symbole wiedergegeben werden. Mit diesen formelhaften Ausdrücken kann
man dann „logisch rechnen“.
Der klassischen Aussagenlogik liegt eine Theorie von den beiden komplementären Wahrheitswerten „wahr“ und „falsch“ zugrunde, wie sie durch die Prinzipien des ausgeschlossenen Widerspruchs und des ausgeschlossenen Dritten bestimmt ist: (1) eine Aussage kann nicht gleichzeitig
wahr und falsch sein und (2) in einer Situation, in der einem Aussagensatz ein Wahrheitswert
zugeordnet wird, muß es einer von beiden sein. Insbesondere gibt es daher zu jeder Aussage „A“
die Verneinung dieser Aussage „non A“, der genau dann der Wahrheitswert „wahr“ zugeordnet
wird, wenn „A“ der Wert „falsch“ zugeordnet wird, und umgekehrt.
Literatur Üblicherweise behandelt jede Einführung in die formale Logik den Kernbestand der
klassischen Aussagenlogik, mit der etwaigen Ausnahme von Werken, die einer Sonderrichtung
der Logik anhängen (etwa dem Intuitionismus). Unter der Vielzahl der Bücher finden sich viele
brauchbare, aber auch viele schlechte. Fühlen Sie sich ermuntert, in der Bibliothek zu stöbern
und ein gutes und ihrem Geschmack entsprechendes Buch zu entdecken, aber lesen Sie mit
kritischen Geist.
Zwei Warnungen sind angebracht. Die erste ist pädagogischer Art: Sowohl die Symbolschreibweise als auch die Begriffe in der Logik sind sehr uneinheitlich. Dieses Skript benutzt die
Schreibweisen, die sich in der mathematischen Logik in den letzten Jahrzehnten weitgehend
als Standardsprache durchgesetzt haben. Eher philosophisch orientierte Werke greifen oft auf
historische Schreibweisen zurück, welchen meist den Nachteil geringerer Lesbarkeit anhängt.
Dies erfordert für viele Bücher eine große Flexibilität bei der Lektüre. Die zweite Warnung ist
grundlegenderer Art: Viele Bücher sind ungeeignet oder sogar schlecht. Seltener, aber dennoch
erschreckend oft, weil die Autoren die Logik, die sie darstellen, nicht verstanden haben. Häufiger liegt das Problem jedoch darin, daß die Autoren die Leser für eine bestimmte Auffassung
der Logik missionieren wollen, manchmal verbunden mit der Entwicklung eines eigenen, vermeintlich besseren Systems, oder sich in zweitrangige Fragen verirren und etwas in die Logik
hineingeheimnissen wollen, was sich dort nicht befindet.
Brauchbare Bücher sind:
• Ansgar Beckermann Einführung in die Logik, 2. Auflage, Berlin: de Gruyter 2003.
Für Leser mit einem weitergehenden und mathematischen Intertesse an der Logik empfehlen
3
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
sich die Einführungen:
• Ebbinghaus, Flum, Thomas Einführung in die mathematische Logik, 5. Auflage, Heidelberg:
Spektrum 2007.
• Cori, Lascar Logique mathématique, Paris: Masson 1993.
Übersicht Zunächst wird in 1.1 die formale Sprache für die Aussagenlogik definiert. In 1.2
wird dann besprochen, wie man Sätzen in der aussagenlogische Sprache Wahrheitswerte zuordnet. Dies erlaubt es, in 1.3 den Begriff „logische Folgerung“ und verwandte Begriffe einzuführen.
Dort findet sich auch eine Liste wichtiger logischer Gesetze. Abschnitt 1.4 begründet dann die
Wahl der formalen Sprache und erläutert einiges über ihre Struktur. Schließlich geht es in 1.5
hauptsächlich um einen alternativen, „syntaktischen“ Zugang zur Aussagenlogik, und in 1.6 um
die Möglichkeit der Übersetzung aus der natürlichen Sprache.
1.1
Die aussagenlogische Sprache
Eine formale Sprache besteht in der Regel aus zwei „Zutaten“: einem Alphabet, also einer Menge
von erlaubten Zeichen oder Symbolen, und einer Grammatik, die erklärt, welche Zeichenfolgen
Sätze der formalen Sprache sind. Wie in einer natürlichen Sprache, die beispielsweise Wörter,
Neben– und Hauptsätze kennt, kann die Grammatik auf mehreren Stufen arbeiten. Dies ist
aber in der Aussagenlogik nicht der Fall: Es gibt dort nichts den Wörtern entsprechendes. Im
Gegensatz zu den natürlichen Sprachen sind die Regeln aber klar und streng: Man muß immer
eindeutig entscheiden können, ob eine Zeichenfolge ein Satz der formalen Sprache ist oder nicht.
Das Alphabet
Die aussagenlogische Sprache setzt sich aus folgenden Zeichen zusammen:
• den Aussagenvariablen A, B, C, . . . (lateinische Majuskeln)1 ;
• den logischen Zeichen ⊥, >, ¬, ∧, ∨, →, ↔;
• den nicht-logischen Zeichen ( und ), also öffnender und schließender Klammer.
Anmerkung: Bei anderen Autoren wird die formale Sprache für die Aussagenlogik meist anders
aussehen. Zunächst kann man ebensogut auch andere Buchstaben oder Zeichen als Aussagenvariablen wählen; wichtig ist nur, daß man sie von den anderen verwendeten Zeichen klar
unterscheiden kann. Dann gibt es eine Vielzahl anderer logischer Zeichen zum Teil mit gleicher
Funktion wie die obigen, zum Teil mit anderer. Dazu später mehr. Auch gibt es formale Sprache,
die mit anderen oder ohne nicht-logische Zeichen auskommen.
Die Grammatik Die aussagenlogischen Sätze oder auch aussagenlogischen Formeln (beide
Ausdrücke werde ich synonym verwenden) werden nach bestimmten Regeln aus einfacheren aussagenlogischen Formeln aufgebaut. Einfachste, nicht mehr zerlegbare aussagenlogische Formeln
sind die Aussagenvariablen und die Aussagenkonstanten > und ⊥. Zusammengesetzte Formeln
werden aus einfacheren Formeln mit Hilfe der Junktoren ¬, ∧, ∨, → und ↔ gebildet. Dabei
bewirken Klammern die Lesbarkeit der Formeln.
Die exakten Regeln sind wie folgt, dabei dienen S und T als Platzhalter für beliebige aussagenlogische Formeln2 :
1 Eigentlich möchte man unbegrenzt viele Aussagenvariablen zur Verfügung haben; falls die 26 Buchstaben
des lateinischen Alphabetes nicht ausreichen, erlaubt man sich auch Varianten davon, etwa indizierte Buchstaben
A1 , A2 oder A0 , A00 u.ä.
2 Und zwar in folgendem Sinne: Eine aussagenlogische Formel ist eine Folge von Zeichen aus dem Alphabet;
wo nun in der folgenden Definition ein solcher Platzhalter für eine aussagenlogische Formel steht, soll man sich
an seiner Stelle die durch ihn repräsentierte Zeichenfolge eingesetzt denken. Die beiden Zeichen „S“ und „T “
selbst sind nicht Teil des aussagenlogischen Alphabets.
4
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
1) Jede Aussagenvariable ist auch eine aussagenlogische Formel.3
2) > und ⊥ sind jeweils eine aussagenlogische Formel.
3) Wenn S eine aussagenlogische Formel ist, dann auch ¬S.
(Genauer formuliert: Wenn eine Zeichenfolge eine aussagenlogische Formel bildet, dann auch
die Zeichenfolge, die man durch Voransetzen eines Negationszeichens erhält.)
4) Wenn S und T aussagenlogische Formeln sind, dann ist auch jede der vier Zeichenfolgen
(S ∧ T ), (S ∨ T ), (S → T ) und (S ↔ T ) eine aussagenlogische Formel.
(Genauer formuliert: Wenn zwei Zeichenfolgen jeweils eine aussagenlogische Formel bilden,
dann ist auch die Zeichenfolge eine aussagenlogische Formel, die man erhält, indem man
erst eine öffnende Klammer, dann die eine Zeichenfolge, dann eines der Zeichen „∧“, „∨“,
„→“„↔“, dann die andere Zeichenfolge, dann eine schließende Klammer schreibt.)
Aussagenlogische Formeln sind nur diejenigen Zeichenfolgen, welche nach diesen Regeln gebildet
werden können.
Beispiele: Aussagenlogische Formeln sind etwa
A
¬¬C
(¬A ∨ B)
¬(A ∨ B)
(> ∧ A)
(C ∧ A)
¬(¬¬¬> ∧ ⊥)
(((A ∧ A) ∧ A) ∧ A)
(¬((¬A ∨ B) ∧ ¬¬B) ∨ (A ∧ ¬⊥))
Namen > heißt das Verum, ⊥ das Falsum.
¬ heißt Negationszeichen oder logisches Nicht, ¬S die Negation oder Verneinung von S, lies
„non S“ (oder „nicht S“, was aber leicht zu Mißverständnissen führen kann).
∨ heißt Disjunktionszeichen oder logisches Oder, (S ∨ T ) die Disjunktion von S und T , lies „S
oder T “.
∧ heißt Konjunktionszeichen oder logisches Und, (S ∧ T ) die Konjunktion von S und T , lies
„S und T “.
→ heißt Implikationszeichen, (S → T ) die Implikation, lies „S impliziert T “.
↔ heißt Bi-implikationszeichen, die Bi-implikation von S und T , lies „S äquivalent T “, „S und
T implizieren sich gegenseitig oder (mathematischer) „S genau dann, wenn T “, „S dann und
nur dann, wenn T “.
Eselsbrücken: ¬ ist einem Minuszeichen ähnlich. > erinnert an das englische True, ∨ an das
lateinische vel. Die dazu „dualen“ Zeichen ⊥ und ∧ entstehen daraus durch Umklappen.
1.1.1
Eindeutige Lesbarkeit
Jede aussagenlogische Formel ist eindeutig lesbar, d.h. sie trägt die Information in sich, wie sie
gebildet wurde. Dies ist keine Selbstverständlichkeit; zum Beispiel ist das Wort „Ersatzbusfahrer“ auf zwei Weisen lesbar: als Fahrer eines Ersatzbusses oder als Busfahrer, der einen Kollegen
3 Eine ähnliche Doppelrolle gibt es in manchen natürlichen Sprachen – einzelne Buchstaben können auch
Wörter sein. Oder bei der üblichen Dezimalschreibweise von Zahlen, wo einzelne Ziffern auch Zahlen darstellen.
5
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
ersetzt. Korrekte Betonung bewirkt normalerweise immerhin eine „eindeutige Hörbarkeit“. Die
eindeutige Lesbarkeit wird bei den Formeln durch die Klammersetzung bewirkt. Es gibt andere Klammersetzungsmethoden; die Wahl ist Geschmacksfrage und willkürlich, muß dann aber
konsequent beachtet werden. Es gibt auch die klammerlose „polnische Notation“, siehe Seite 7.
Im Falle der letzten Formel unter den obigen Liste an Beispielen:
• (¬((¬A ∨ B) ∧ ¬¬B) ∨ (A ∧ ¬⊥)) entsteht aus ¬((¬A ∨ B) ∧ ¬¬B) und (A ∧ ¬⊥) mit
Regel 4.
• (A ∧ ¬⊥) entsteht aus A und ¬⊥ mit Regel 4; A ist eine aussagenlogische Formel nach
Regel 1 und ¬⊥ entsteht mit Regel 3 aus ⊥, was als aussagenlogische Konstante nach
Regel 2 eine aussagenlogische Formel ist.
• ¬((¬A ∨ B) ∧ ¬¬B) entsteht aus ((¬A ∨ B) ∧ ¬¬B) mit Regel 3; ((¬A ∨ B) ∧ ¬¬B) ensteht
aus (¬A ∨ B) und ¬¬B mit Regel 4.
• ¬¬B entsteht aus ¬B mit Regel 3; dies wiederum aus B mit Regel 3, und B ist eine
aussagenlogische Formel nach Regel 1.
• (¬A ∨ B) entsteht aus ¬A und B nach Regel 4; ¬A wiederum aus A nach Regel 3; und A
und B waren bereits als aussagenlogische Formeln gemäß Regel 1 identifiziert.
Dies kann man sich graphisch gut veranschaulichen in einem sogenannten Formelbaum in Abbildung 1.1.
Abbildung 1.1: Formelbaum
(¬((¬A ∨ B) ∧ ¬¬B) ∨ (A ∧ ¬⊥))
@
R
@
¬((¬A ∨ B) ∧ ¬¬B)
?
((¬A ∨ B) ∧ ¬¬B)
@
R
@
(¬A ∨ B)
@
R
@
¬A
?
A
B
(A ∧ ¬⊥)
@
R
@
A
¬¬B
?
¬B
¬⊥
?
⊥
?
B
Im allgemeinen muß man den Aufbau einer Formel rückwärts nachvollziehen:
• Entweder sie besteht nur aus einem Zeichen und ist durch Regel 1 oder 2 gegeben.
• Oder das am weitesten links stehende Zeichen ist ein ¬ und sie ist aus Regel 3 entstanden.
• Oder die Formel wird von einem Klammerpaar umfaßt: dann wurde sie mit Regel 4 gebildet. Welches der dafür richtige Junktor ist, erkennt man folgendermaßen: Bildet man
die Regel zurück, zerlegt also die Formel durch Entfernen der äußersten Klammern und
des Junktors in zwei Teile, so müssen in jedem Teil ebenso viele öffnende wie schließende
Klammern verbleiben.
Beispiel: Die Formel (¬((¬A ∨ B) ∧ ¬B) ∨ A) kann nicht zuletzt durch Regel 4 aus ¬((¬A ∨ B)
und ¬B) ∨ A entstanden sein, weil dann in den Einzelteilen die Klammerung nicht stimmt.
6
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Die Zwischenstufen im Entstehungsprozeß einer aussagenlogischen Formel S, also die im Beispiel
in dem Formelbaum auftretenden Formeln, heißen auch die Teilformeln oder Subformeln von S.
Üblicherweise zählt man die Formel selbst auch zu ihren Teilformeln; will man sie ausschließen,
spricht man auch von echten oder eigentlichen Teilformeln.
Beispiel: Die Subformeln von ((¬A∨B) → ⊥) sind A, B, ⊥, ¬A, (¬A∨B) und ((¬A∨B) → ⊥).
1.1.2
Andere Schreibweisen
Wie schon erwähnt, findet sich in der Literatur eine Fülle anderer Namen und Schreibweisen vor
allem für die Junktoren, da es leider (noch) keine allgemein akzeptierte Standardsprache gibt.
Dieser Abschnitt versucht, einige andere mehr oder wengier verbreitete Namen und Zeichen zu
versammelt als Lesehilfe für andere Werke; er trägt nichts zum Verständnis des Skriptes bei.
Mehr in:
• Carol Horn Greenstein Dictionary of Logical Terms and Symbols, New York: 1978.
Die Disjunktion wird hier für das einschließende Oder stehen; bei anderen Autoren steht dieser
Begriff (etymologisch korrekter) für das ausschließende Oder, für das einschließende dann „Adjunktion“. Statt „Implikation“ bevorzugen einige „Subjunktion“ oder „Konditional“. Gebräuchlicher als „Bi-implikation“ ist „Äquivalenz“, führt aber leicht zu Verwechselungen mit der auf
Seite 10 eingeführten logischen Äquivalenz zweier Formeln.
Es folgt eine Liste alternativer Zeichen für die Junktoren. Am wichtigsten ist sicherlich das
Peanosche (A ⊃ B) für die Implikation (A → B). Die Notationen von Łukasiewicz benutzen
Großbuchstaben für die Junktoren, daher stehen dort p und q für Aussagenvariablen.
Verum
Falsum
Negation
Konjunktion
Disjunktion
Implikation
Bi-implikation
↑, 1, V, W; fehlt auch oft
↓, 0, Λ, F; fehlt auch oft
∼ A, −A, A, A0 , N p
(A&B), (A · B), (A × B), (AB), (A ∩ B), Kpq
(A|B), (A + B), (A ∪ B), Apq
(A ⇒ B), (A ⊃ B), (A : B), Cpq
(A ⇔ B), (A ≡ B), (A ⊃⊂ B), (A = B), (A ∼ B), (A u B), Epq
Klammern werden oft anders gesetzt. Zum Beispiel kann man bei Anwendung von Junktoren
statt äußeren Klammern auch die zu verbindenden Teilformeln jeweils in Klammern fassen, also
etwa (S) ∧ (T ) statt (S ∧ T ). Außerdem gibt es bei vielen Autoren Klammersparregeln, indem
etwa äußere Klammern weggelassen werden oder eine Reihenfolge in der Bindungsstärke der
Junktoren eingeführt wird.
Daneben ist auch die von Peano erfundene und in der Principia Mathematica verwendete Punktschreibweise verbreitet: Je mehr Punkte ein Junktor trägt, desto später kam er beim Aufbau
der Formel hinzu. Beispiel: A . → . B → C statt ((A → B) → C). Außerdem gibt es die
klammerfreien Formelschreibweisen von Łukasiewicz: die polnische und die umgekehrt polnische
Notation. Dabei werden die Junktoren vor bzw. hinter die durch sie verbundenen Teilformeln
statt dazwischen geschrieben. Die Formel (¬((¬A ∨ B) ∧ ¬¬B) ∨ (A ∧ ¬⊥)) schreibt sich dann
∧¬ ∧ ∨¬AB¬¬B ∧ A¬⊥ bzw. A¬B ∨ B¬¬ ∧ ¬A⊥¬ ∧ ∨. Der Vorteil der Klammerfreiheit ist
durch eine zwar noch eindeutige, aber dennoch offensichtlich mühsamere Lesbarkeit erkauft.
Das Problem der Klammerung entsteht dadurch, daß eine Formel eigentlich ein zweidimensionales Gebilde ist, welches am besten in der Form eines Baumes wie in Abbildung 1.1 dargestellt
würde (was zum Beispiel Frege in seiner Begriffsschrift tut), mit den offensichtlichen Nachteilen.
Das Herunterbrechen dieser zweidimensionalen Form in eine Folge von Zeichen ist nicht ohne
Kompromisse möglich. Eine Mischform aus ein– und zweidimensionaler Schreibweise erhält man,
wenn man die Negation durch einen Überstrich darstellt, im Beispiel: (((A ∨ B) ∧ B)∨(A∧⊥)).
7
M. Junker „Formale Logik“
1.2
Version vom 10. Dezember 2012
Wahrheitswerte
Bislang haben wir mit den aussagenlogischen Formeln lediglich bedeutungslose Zeichenfolgen
geschaffen. Nun sollen ihnen Wahrheitswerte in Abhängigkeit von Wahrheitswerten für die darin
auftauchenden Aussagenvariablen zugeordnet werden. Dies geschieht gemäß der Bildungsgesetze
der Formeln. Die Wahrheitswerte „wahr“ und „falsch“ werden mit W und F beschrieben.
Die logischen Konstanten > und ⊥ bekommen unabhängig von den Wahrheitswerten der
Aussagenvariablen stets den Wahrheitswert W bzw. F zugeordnet.
Als Wahrheitstafel:
>
W
⊥
F
Die Negation: Ist S eine aussagenlogische Formel, so bekommt ¬S den Wahrheitswert W
zugeordnet, wenn S den Wahrheitswert F erhält, und ¬S bekommt den Wahrheitswert F zugeordnet, wenn S den Wahrheitswert W erhält.
Als Wahrheitstafel:
S
W
F
¬S
F
W
Konjunktion und Disjunktion: Sind S und T aussagenlogische Formeln, so bekommt
(S ∧ T ) den Wahrheitswert W zugeordnet, wenn sowohl S als auch T den Wahrheitswert W
erhalten, und F in allen anderen Fällen. (S ∨ T ) bekommt den Wahrheitswert F zugeordnet,
wenn sowohl S als auch T den Wahrheitswert F erhalten, und W in allen anderen Fällen.
Implikation: Sind S und T aussagenlogische Formeln, so bekommt (S → T ) den Wahrheitswert F zugeordnet, wenn S den Wahrheitswert W und T den Wahrheitswert F erhält, und W
in allen anderen Fällen.
Bi-implikation: Sind S und T aussagenlogische Formeln, so bekommt (S ↔ T ) den Wahrheitswert W zugeordnet, wenn S und T den gleichen Wahrheitswert erhalten, und (S ↔ T )
bekommt den Wahrheitswert F zugeordnet, wenn S und T verschiedene Wahrheitswert erhalten.
Als Wahrheitstafeln:
1.2.1
S
W
W
F
F
T
W
F
W
F
(S ∧ T )
W
F
F
F
(S ∨ T )
W
W
W
F
(S → T )
W
F
W
W
(S ↔ T )
W
F
F
W
Belegungen und Auswertungen von aussagenlogischen Formeln:
Ist eine aussagenlogische Formel S gegeben, so heißt jede Zuordnung von Wahrheitswerten zu
den in der Formel auftretenden Aussagenvariablen eine Belegung. Da mit den Aussagenvariablen keine inhaltliche Bedeutung verknüpft ist, ist jede Belegung gleichermaßen sinnvoll. Bei
n Aussagenvariablen gibt es also 2n Belegungen. Durch die eindeutige Lesbarkeit liefert eine
Formel ein Verfahren, wie ihr unter einer Belegung selbst ein Wahrheitswert zukommt. Dabei
werden nach und nach die Teilformeln so ausgewertet, wie die Wahrheitstafeln der Junktoren
es vorgeben. Man hangelt sich gewissermaßen von „unten“, d.h. den Aussagenvariablen und –
konstanten, den ganzen Formelbaum entlang nach „oben“, d.h. zu der gegebenen Formel. Das
Ergebnis nennt man den Wahrheitswertverlauf der Formel, zusammen mit den Zwischenergebnissen die vollständige Wahrheitstafel.
Beispiel: S sei die Formel (¬((¬A∨B)∧¬¬B)∨(A∧¬⊥)). Es folgt die vollständige Wahrheitstafel
für S; den Wahrheitswertverlauf von S findet man in der letzten Spalte:
8
M. Junker „Formale Logik“
A
W
W
F
F
B ¬A (¬A ∨ B)
W F
W
F F
F
W W
W
F W
W
Version vom 10. Dezember 2012
¬B ¬¬B ((¬A ∨ B) ∧ ¬¬B) ¬((¬A ∨ B) ∧ ¬¬B)
F W
W
F
W F
F
W
F W
W
F
W F
F
W
⊥
F
F
F
F
¬⊥ (A ∧ ¬⊥)
W
W
W
W
W
F
W
F
S
W
W
F
W
Eine kompaktere Schreibweise, welche das Aufführen sämtlicher Teilformeln vermeidet, aber weniger übersichtlich ist, besteht darin, die Wahrheitswerte jeweils unter den betreffenden Junktor
zu schreiben. Die Spalte, welche den Wahrheitswertverlauf für S liefert, muß dann gesondert
gekennzeichnet werden.
A
W
W
F
F
B
W
F
W
F
(¬ ((
F
W
F
W
¬
F
F
W
W
A
W
W
F
F
∨
W
F
W
W
B)
W
F
W
F
∧
W
F
W
F
¬
W
F
W
F
¬
F
W
F
W
B)
W
F
W
F
∨ ( A ∧ ¬ ⊥))
W WWWF
W WWWF
F F F WF
W F F WF
Man sieht, daß das Aufstellen einer vollständigen Wahrheitstafel für eine große Formel einen
immensen Arbeitsaufwand bedeutet. Bei n Variablen und m Junktoren in der Formel, muß man
2n · m Wahrheitswerte hinschreiben, dies sind z.B. bei 10 Aussagenvariablen und 30 Junktoren
bereits 30720 Einträge, wofür man bei einem Wert pro Sekunde über 8 Stunden braucht. Bei
einer doppelt so großen Formel, 20 Aussagenvariablen und 60 Junktoren, bräuchte man bereits
zwei Jahre! Um das Ergebnis unter einer einzigen Belegung zu erhalten, muß man dagegen nur
die betreffende Zeile ausrechnen, was schnell geht.
Mit gewissen Überlegungen kann man etwas Arbeit sparen. Es ist klar, daß Aussagenvariablen,
die in einer Formel nicht auftreten, für die Auswertung auch keine Rolle spielen. Im Beispiel
hängen die Werte für (A ∧ ¬⊥) nicht von B ab: Zwei Belegungen, die sich nur auf B unterscheiden, liefern den gleichen Wahrheitswert. Man kann sich für diese Teilformel also zwei Zeilen
sparen. Ebenso kennt man das Gesamtergebnis einer Disjunktion oder Konjunktion, wenn für
ein Disjunktions– bzw. Konjunktionsglied bereits ein Wahrheitswert W bzw. F vorliegt. Im
Beispiel würden also folgende Wahrheitswerte genügen, wenn man bei jeder Disjunktion und
Konjunktion zunächst die kürzere Seite auswertet (dazu muß man aber die Formel „von oben
nach unten“ durchlaufen, wobei man leicht den Überblick verlieren kann – günstiger ist hier die
Darstellung als Formelbaum):
A
W
W
F
F
B
W
F
W
F
(¬ (( ¬ A ∨ B ) ∧ ¬ ¬ B ) ∨ ( A ∧ ¬ ⊥))
W
W W W F
W
F
WW WW F W F
F F
W
F F WF W
Es gibt aber kein bekanntes Verfahren, und man vermutet stark, daß es keines geben kann,
welches für eine beliebige Formel schnell entscheidet, ob sie einen gegebenen Wahrheitswertverlauf besitzt. In der zwischen mathematischer Logik und theoretischer Informatik angesiedelten
Komplexitätstheorie bekommen diese Fragen eine präzise Bedeutung und spielen eine wichtige
Rolle (sogenannten „P = NP“–Problem).
1.2.2
Modelle und Interpretationen:
Ein Modell M besteht aus
1) einem Universum, das ist ein festgelegter Denk– oder Aussagenbereich, auf den sich Aussagen
beziehen werden, und
2) für jede auftretende Aussagenvariable aus der Wahl einer Aussage, welche in diesem Universum (zumindest theoretisch) als wahr oder falsch erkannt werden kann.
9
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Ein Modell liefert also eine Interpretation jeder Aussagenvariablen durch eine Aussage und damit eine Belegung der Aussagenvariablen. Umgekehrt kann man leicht zu jeder Belegung ein
Modell finden, welches diese Belegung liefert. Ein Modell ist somit eine Konkretisierung einer
Belegung. Indem man den Aufbau einer Formel nachvollzieht, interpretiert das Modell auch
jede aussagenlogische Formel durch eine Aussage. In einem Modell kann somit jeder aussagenlogischen Formel ein Wahrheitswert, W oder F, zugeordnet werden.
Man schreibt M S, falls die aussagenlogische Formel S in dem Modell M den Wert W
zugeordnet bekommt, und sagt, M sei ein Modell von S oder M erfüllt S oder auch S gilt
in M. Ist M kein Modell von S, d.h. bekommt S in M den Wahrheitswert F zugeordnet, so
schreibt man M 6 S. Entsprechend schreibt man M Σ für eine Formelmenge Σ, falls jede
Formel aus Σ in M gilt, und M 6 S, falls M kein Modell von S ist. Dazu reicht es aus, daß
eine Formel aus Σ in M nicht gilt!
Achtung: Weder der Buchstabe M noch das Zeichen sind Teil der aussagenlogischen Sprache.
„M“ ist eine Name für ein Modell, „“ eine abkürzende Schreibweise für „ist Modell von“.
Beispiel: Das Universum des Modells sei Deutschland, die vorkommenden Aussagenvariablen
A, B, C werden durch Freiburg wurde von den Herzogen von Zähringen gegründet, In Freiburg
gibt es eine Universität beziehungsweise Freiburg liegt an der Saane interpretiert. Dann ist
dies ein Modell von ((A ∧ B) ∧ ¬C). Wäre bei gleicher Interpretation der Aussagenvariablen
das Universum die Schweiz, so hätte man kein Modell dieser Formel, aber ein Modell von
((A ∧ B) ∧ C).
1.3
Aussagen über Sätze und Metasprache
Eine aussagenlogische Formel heißt eine Tautologie, wenn ihr unter allen Belegungen der darin vorkommenden Aussagenvariablen der Wahrheitswert W zukommt, und Antilogie, wenn ihr
unter allen Belegungen der darin vorkommenden Aussagenvariablen der Wahrheitswert F zukommt.
Eine aussagenlogische Formel S (bzw. eine Menge Σ aussagenlogischer Formeln) heißt erfüllbar
oder konsistent, wenn es mindestens eine Belegung der vorkommenden Aussagenvariablen gibt,
unter der S (bzw. alle Sätze in Σ) den Wahrheitswert W zugeordnet bekommen.
Eine aussagenlogische Formel T folgt logisch aus einer aussagenlogischen Formel S oder aus
einer Menge Σ aussagenlogischer Formeln, falls T wahr wird unter allen Belegungen der vorkommenden Aussagenvariablen, unter denen S bzw. alle Formeln in Σ wahr werden.
Zwei aussagenlogische Formeln S und T heißen logisch äquivalent, wenn ihnen unter allen Belegungen der darin vorkommenden Aussagenvariablen der gleiche Wahrheitswert zukommt, und
logisch kontravalent, wenn ihnen unter allen Belegungen der darin vorkommenden Aussagenvariablen verschiedene Wahrheitswerte zukommen.
Die Begriffe „Antilogie“ und „logisch kontravalent“ stehen mehr der Vollständigkeit halber hier;
sie sind von geringerem Gebrauch.
Beispiele: (A ∨ ¬A) und (((A → B) ∧ A) → B)) sind Tautologien; (A ∧ ¬A) eine Antilogie.
(A ∧ B) ist eine erfüllbare Formel, die keine Tautologie ist.
A ist logisch äquivalent zu ¬¬A und auch zu (A ∧ A); (A ∧ B) ist logisch äquivalent zu (B ∧ A).
A folgt logisch aus (A ∧ B), aber nicht umgekehrt, wohingegen (A ∧ B) logisch aus der Menge
Σ, die aus A und B besteht, folgt.
Aus ⊥ folgt logisch jeder beliebige Satz; dual dazu folgt > logisch aus jedem anderen Satz.
Kurzschreibweisen: Für „S ist eine Tautologie“ kann man abkürzend „` S“ schreiben. Für
„T folgt logisch aus S“ kann man „S ` T “ schreiben; entsprechend für eine Formelmenge Σ
anstelle von S. Schließlich stehe „S ∼ T “ für „S und T sind logisch äquivalent“.
Die Benutzung desselben Zeichens ` für Tautologien und logische Folgerung rechtfertigt sich
folgendermaßen: In ` S steht links des Zeichens die leere Menge an aussagenlogischen Sätzen,
10
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
und ein Satz S ist genau dann eine Tautologie, wenn S logisch aus der leeren Menge aussagenlogischer Formeln folgt.
Für die anderen Begriffe werden hier keine eigenen Zeichen eingeführt. Man kann jedoch die
„verneinten Zeichen“ 0 und einführen; dann kann man zum Beispiel 0 ¬S dafür schreiben,
daß S erfüllbar ist, wie aus den unten ausgeführten Zusammenhängen hervorgeht.
Warnung! Die Zeichen ` und ∼ sind nicht Teil der aussagenlogischen Sprache! Zum Beispiel
sind A ∼ (A ∨ A) und ` (A → A) keine aussagenlogischen Formeln, sondern Aussagen über
aussagenlogische Formeln. Hier muß man sich die Erörterungen von Seite ?? in Erinnerung
rufen:
Im Gegensatz zu den Gewohnheiten beim Gebrauch der natürlichen Sprache unterscheidet man
in der formalen Logik genau zwischen einerseits rein syntaktischen Objekten (Zeichenfolgen),
also den Formeln, die keine Bedeutung an sich tragen und die hinzuschreiben keine Aussage beinhaltet, und andererseits Aussagen über diese Objekte. Diese Unterscheidung ist schon
deshalb notwendig, da in den aussagenlogischen Formeln in der Regel Aussagenvariablen vorkommen und der Wahrheitswert der Formel von der Belegung der Aussagenvariablen abhängt.
Eine Aussage wie „(A ∧ B) ist wahr“ ist außerhalb eines Modelles sinnlos, also solange A und
B nicht Wahrheitswerte oder Bedeutungen zugeordnet werden.
Die verschiedenen Ebenen, die man in der natürlichen Sprache durch den Gebrauch von Anführungszeichen kennzeichnen würde, werden in der Aussagenlogik zunächst dadurch transparent,
daß die aussagenlogischen Sätze in der besonderen formalen Sprache geschrieben werden, die
Aussagen über diese Sätze in natürlicher Sprache. Man kann sich bei einer Aussage über aussagenlogische Sätze also jeden solchen als in Anführungszeichen stehend vorstellen. Diese äußerliche Unterscheidung der verschiedenen Ebenen droht durch die Einführung der Zeichen ` und ∼
zu verwischen; daher sollte man sie sparsam benutzen, zumindest, solange man noch unsicher
im Umgang mit aussagenlogischen Formeln ist. ` und ∼ kann man als Symbole einer anderen formalen Sprache (der Metasprache im Gegensatz zur aussagenlogischen Objektsprache)
verstehen.
Der etwas unübliche Name „Bi-implikation“ anstelle des üblicheren „Äquivalenz“ soll auch
sprachlich die Verschiedenheit von ↔ und ∼ hervorheben. Wegen des Zusammenhangs zwischen logischer Äquivalenz zweier Formeln und ihrer Bi-implikation in 4) unten wäre es jedoch
vergleichsweise unproblematisch, die Bi-implikation auch als Äquivalenz zu bezeichnen.
Andere Schreibweisen Das Tautologie– und Folgerungszeichen ` wurde von Frege in der
Begriffsschrift eingeführt, der damit als erster eine klare notationelle Unterscheidung zwischen
einem Satz und der durch den Satz beschriebenen Aussage einführte. Stattdessen steht oft auch
, als Folgerungszeichen auch ⇒.
Viele Autoren unterscheiden zunächst zwischen einer wie hier semantisch, d.h. über Modelle begründeten Folgerungsbeziehung, die dann mit bezeichnet wird, und einer syntaktisch,
d.h. durch einen Beweiskalkül (siehe Abschnitt 1.5.3) begründeten Folgerungsbeziehung `. Der
Vollständigkeitssatz für den betreffenden Kalkül erlaubt es dann, beide zu identifizieren.
Für die logische Äquivalenz gibt es auch die Zeichen ⇔, a` oder =||=. Auch in der mathematischen Logik ist ∼ kein Standardzeichen. (Das dort häufig benutzte ⇐⇒ drückt in der Regel
eine logische Äquivalenz zwischen Aussagen aus, also noch eine Ebene höher).
1.3.1
Zusammenhänge
Man kann jeden der Begriffe – Tautologie, Antilogie, Erfüllbarkeit, logische Folgerung, logische
Äquivalenz – auf jeden der anderen zurückführen, ohne erneut über Wahrheitswerte sprechen
zu müssen.
Zunächst ist zu bemerken, daß Tautologien Spezialfälle erfüllbarer Formeln darstellen; Antilogien sind genau die nicht erfüllbaren, d.h. inkonsistenten Sätze. Antilogie ist also ein Gegensatz
11
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
zu Tautologie, aber das Gegenteil einer erfüllbaren Formal.
1) S ist dann und nur dann eine Tautologie, wenn ¬S eine Antilogie ist.
S ist dann und nur dann eine Antilogie, wenn ¬S eine Tautologie ist.
S ist dann und nur dann erfüllbar, wenn ¬S keine Tautologie ist.
2) S ist dann und nur dann eine Tautologie, wenn S und > logisch äquivalent sind,
und dann und nur dann, wenn S logisch aus > folgt.
S ist dann und nur dann eine Antilogie, wenn S und ⊥ logisch äquivalent sind,
und dann und nur dann, wenn ⊥ logisch aus S folgt.
3) Eine aussagenlogische Formel T folgt dann und nur dann logisch aus S, wenn (S → T ) eine
Tautologie ist.
4) Zwei aussagenlogische Formeln S und T sind dann und nur dann logisch äquivalent, wenn
(S ↔ T ) eine Tautologie ist.
5) Zwei aussagenlogische Formeln S und T sind dann und nur dann logisch äquivalent, wenn
T logisch aus S folgt und S logisch aus T folgt.
Tabellarisch sei nun zusammengefaßt, wie man die Begriffe Tautologie, Antilogie, logische Folgerung und logische Äquivalenz auseinander erklären kann; dabei stehen in jeder Zeile drei
verschiedene Weisen, den vorne stehenden Begriff in metasprachlicher Kurzschreibweise zu beschreiben:
Tautologie
Antilogie
logische Folgerung
logische Äquivalenz
`S
` ¬S
` (S → T )
` (S ↔ T )
>
S
S
>
`S
`⊥
`T
` (S ↔ T )
S
S
(S → T )
S
∼>
∼⊥
∼>
∼T
Anmerkungen: Die obigen Sätze haben selbst die Form einer Äquivalenz. Setzt man in 4) A
für „zwei aussagenlogische Formeln S und T sind logisch äquivalent“ und B für „(S ↔ T ) ist
eine Tautologie“, so hat der Satz die Form (A ↔ B) und sagt A ∼ B aus.
Man beachte, daß in 4) drei verschiedene Arten der Äquivalenz auftreten: (a) die rein syntaktische Äquivalenz (Bi-implikation) im Zeichen ↔; (b) die logische Äquivalenz zwischen S und T ,
ausgedrückt im Zeichen ∼; (c) schließlich die (ebenfalls logische) Äquivalenz des Gesamtsatzes,
welche die Gleichwertigkeit von zwei Aussagen über aussagenlogische Sätze behauptet, ausgedrückt im „dann und nur dann, wenn“. (Für letzteres schreibt man in der Mathematik oft ⇐⇒
für „dann und nur dann, wenn“. Noch kürzer könnte man 4) also als S ∼ T ⇐⇒ ` (S ↔ T )
schreiben. Man sieht daran einerseits schön den Unterschied der drei Äquivalenzzeichen ↔, ∼
und ⇐⇒ . Andererseits erkennt man an der ersten Anmerkung, daß die Frage, auf welcher Ebene man sich befindet, also welches Zeichen angebracht ist, keine absolute Antwort hat, sondern
daß es nur um den relativen Bezug der Ebenen untereinander geht.)
1.3.2
Einige logische Gesetze
Durch Ausrechnen von Wahrheitstafeln kann man stets testen, ob zwei Formeln logisch äquivalent sind. Einfacher geht es aber oft, wenn man grundlegende Regeln kennt: Dann kann man
manchmal leicht eine Formel in mehreren Schritten in eine andere, logisch äquivalente umformen. Es folgen eine umfangreiche Liste grundlegender Äquivalenzen (sowie einiger Tautologien
und logischen Folgerungen), von denen manche auch ein eigenständiges Interesse haben, sowie
zwei Substitutionsprinzipien, welche es erlauben, diese grundlegenden Äquivalenzen auch im
Falle komplizierterer Formeln auszunutzen.
12
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Die Austausch– oder Substitutionsregeln Zunächst sollte man sich folgendes überlegen:
Wenn man in einer aussagenlogischen Formel eine Teilformel durch eine andere Formel ersetzt,
dann entsteht insgesamt wieder eine aussagenlogische Formel. Es gelten nun die beiden wichtigen
Regeln:
Uniforme Substitution: Wenn man in einer Tautologie (oder in zwei logisch äquivalenten Sätzen,
oder in allen Sätzen einer logischen Folgerung Σ ` S) jedes Vorkommen einer Aussagenvariablen
durch dieselbe aussagenlogische Formel ersetzt, so erhält man wieder eine Tautologie (bzw. zwei
logisch äquivalente Sätze oder eine Beziehung logischer Folgerung).
Äquivalente Substitution: Wenn man in einer Tautologie (oder in zwei logisch äquivalenten
Sätzen, oder in allen Sätzen einer logischen Folgerung Σ ` S) irgendeine Teilformel durch eine
dazu logisch äquivalente Formel ersetzt, so erhält man wieder eine Tautologie (bzw. zwei logisch
äquivalente Sätze oder eine Beziehung logischer Folgerung).
Beide Regeln ergeben sich daraus, daß die Konzepte Tautologie, logische Folgerung und logische
Äquivalenz nur von den Wahrheitswertverteilungen abhängen.
Beispiele: a) Aus den beiden Sätzen (A → B), (B → C) folgt logisch (A → C). Ersetzt man
A durch (B ∨ (D → A)) und gleichzeitig B durch (A ∧ B), so erhält man, daß aus den beiden
Sätzen ((B ∨ (D → A)) → (A ∧ B)) und ((A ∧ B) → C) logisch der Satz ((B ∨ (D → A)) → C)
folgt.
b) (A∨¬A) ist eine Tautologie. Ersetzt man das zweite A durch das logisch äquivalente (A∧A),
erhält man eine Tautologie (A ∨ ¬(A ∧ A)).
Die nun folgenden Tautologien, logischen Folgerungen und Äquivalenzen beschreiben die wichtigsten Eigenschaften der Junktoren.
Eigenschaften von > und ⊥ (siehe auch Seite 24)
Definition
`
>
(A ∧ >)
∼
A
A
`
>
Dualität
>
Neutralität
Absorption
verum ex quodlibet/ex falso quodlibet
(A ∨ >)
∼
∼
¬⊥
>
`
¬⊥
⊥
∼
¬>
(A ∧ ⊥)
∼
⊥
(A ∨ ⊥)
⊥
∼
`
A
A
Eigenschaften der Negation
Doppelnegationsregel
ausgeschl. Drittes/ausgeschl. Widerspruch
reductio ad absurdum
¬¬A ∼ A
` (A ∨ ¬A)
(A → ¬A) ∼ ¬A
` ¬(A ∧ ¬A)
(¬A → A) ∼ A
Eigenschaften der Konjunktion und Disjunktion
Monotonie
idempotent
kommutativ
assoziativ
distributiv
de Morgan
Absorption
(A ∧ B) ` A
A ` (A ∨ B)
(A ∧ A) ∼ A
(A ∨ A) ∼ A
(A ∧ B) ∼ (B ∧ A)
((A ∧ B) ∧ C) ∼ (A ∧ (B ∧ C))
((A ∧ B) ∨ C) ∼ ((A ∨ C) ∧ (B ∨ C))
¬(A ∧ B) ∼ (¬A ∨ ¬B)
(A ∧ (A ∨ B)) ∼ A
(A ∨ B) ∼ (B ∨ A)
((A ∨ B) ∨ C) ∼ (A ∨ (B ∨ C))
((A ∨ B) ∧ C) ∼ ((A ∧ C) ∨ (B ∧ C))
¬(A ∨ B) ∼ (¬A ∧ ¬B)
(A ∨ (A ∧ B)) ∼ A
13
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Eigenschaften der Implikation
Identität/—
Definition
Kontraposition
Fallunterscheidung
Transitivität
(nicht assoziativ)
` (A → A)
(A → ¬A) ∼ ¬A
(A → B) ∼ (¬A ∨ B)
(A → B) ∼ ¬(A ∧ ¬B)
(A → ¬B) ∼ (B → ¬A)
(¬A → B) ∼ (¬B → A)
(A → B) ∼ (¬B → ¬A)
` ((A → B) ∨ (¬A → B))
(A → B), (B → C) ` (A → C)
` ((A → B) ∨ (A → ¬B))
(A → (B → C)) ∼ ((A ∧ B) → C)) ∼ ((A → B) → (A → C))
((A → B) → C) ∼ ((¬A → C) ∧ (B → C))
(Anti–)Distributivität
(A → (B ∧ C)) ∼ ((A → B) ∧ (A → C))
(A → (B ∨ C)) ∼ ((A → B) ∨ (A → C))
((A ∧ B) → C) ∼ ((A → C) ∨ (B → C))
((A ∨ B) → C) ∼ ((A → C) ∧ (B → C))
Eigenschaften der Bi-implikation
(A ↔ B) ∼ ((A → B) ∧ (B → A)) ∼ ((¬A ∨ B) ∧ (A ∨ ¬B)) ∼ ((A ∧ B) ∨ (¬A ∧ ¬B))
Identität/—
kommutativ/assoziativ
Kontraposition
Transitivität
Kongruenz
` (A ↔ A)
` ¬(A ↔ ¬A)
(A ↔ B) ∼ (¬A ↔ ¬B)
¬(A ↔ B) ∼ (¬A ↔ B) ∼ (A ↔ ¬B)
(A ↔ B) ∼ (B ↔ A)
((A ↔ B) ↔ C) ∼ (A ↔ (B ↔ C))
(A ↔ B), (B ↔ C) ` (A ↔ C)
(A ↔ C), (B ↔ D) ` ((A ∧ B) ↔ (C ∧ D))
(A ↔ C), (B ↔ D) ` ((A ∨ B) ↔ (C ∨ D))
(A ↔ C), (B ↔ D) ` ((A → B) ↔ (C → D))
Negationstechniken und Dualität Ist S ein zusammengesetzter aussagenlogischer Satz, so
kann man mit den logischen Gesetzen einen zur Negation ¬S logisch äquivalenten Satz finden,
indem man die Negation „nach innen zieht“. Dazu braucht man die Regeln:
„Dualität“
Doppelnegation
de Morgan
Verneinung der Implikation
Verneinung der Bi-implikation
¬>
¬¬S
¬(S ∧ T )
¬(S ∨ T )
¬(S → T )
¬(S ↔ T )
∼
∼
∼
∼
∼
∼
Beispiel: ¬((A → B) ∧ (¬A ∨ (⊥ ↔ B))) ∼
∼
∼
∼
⊥
¬⊥ ∼ >
S
(¬S ∨ ¬T )
(¬S ∧ ¬T )
(S ∧ ¬T )
(¬S ↔ T ) ∼ (S ↔ ¬T )
(¬(A → B) ∨ ¬(¬A ∨ (⊥ ↔ B)))
((A ∧ ¬B) ∨ (¬¬A ∧ ¬(⊥ ↔ B)))
((A ∧ ¬B) ∨ (A ∧ (¬⊥ ↔ B)))
((A ∧ ¬B) ∨ (A ∧ (> ↔ B)))
Dies könnte man noch weiter umformen zu ((A ∧ ¬B) ∨ (A ∧ B)) ∼ (A ∧ (¬B ∨ B)) ∼ A.
Die de–Morganschen–Regeln kann man ausweiten zu einem allgemeineren Dualitätsprinzip:
Wenn S eine Formel ist, in der nur die Junktoren ¬, ∧, ∨ auftreten und die Negationszeichen
¬ nur direkt vor Aussagenvariablen, so erhält man eine zu ¬S logisch äquivalente Formel dadurch, daß man alle Vorkommen von ∧ und ∨ vertauscht, alle Negationszeichen löscht und alle
Aussagenvariablen, die in S ohne Negationszeichen standen, mit einem solchen versieht.
Beispiel: ¬((A∧(¬C ∨B))∨((C ∧¬B)∨(A∧¬C))) ∼ ((¬A∨(C ∧¬B))∧((¬C ∨B)∧(¬A∨C)))
Dieses Dualitätsprinzip kann man auch auf die anderen Junktoren ausdehnen, sofern man alle
denkbaren zweistelligen Junktoren zuläßt (siehe den betreffenden Abschnitt auf Seite 18). Dann
sind dual zueinander:
14
M. Junker „Formale Logik“
> und ⊥
↔ und =
1.3.3
Version vom 10. Dezember 2012
∧ und ∨
→ und 8
∧| und ∨|
← und 9
Fehlerquellen
Auf die wichtigsten Fehlschlüsse wird in Abschnitt 1.5.2 hingewiesen: Meist wird dabei in der ein
oder anderen, oft versteckten Weise aus einer Implikation (A → B) die Gegenrichtung (B → A)
gefolgert, bisweilen aus einer Verwechlsung der Implikation mit der Bi-implikation heraus (siehe
dazu auch die Anmerkungen zu Implikation und Bi-implikation in Abschnitt 1.6.
Ein weiterer beliebter Fehler ist die Verwechselung von ein– und ausschließendem Oder, was,
wie unten erläutert, gewissermaßen der gleiche Fehler ist.
Schließlich passieren gerne Fehler durch falsche Anwendung der Regeln von de Morgan, oder
allgemeiner falschen Verneinungen zusammengesetzter Formeln, oder auch dadurch, daß man
durch fehlerbehaftetes intuitives Verständnis logische Äquivalenzen vermutet, wo keine vorliegen. Etwa neigt man dazu, ((A → C) ∧ (B → C)) umzuformen in ((A ∧ B) → C), es muß aber
((A ∨ B) → C) werden: Da die linke Seite einer Implikation gewissermaßen die verneinte Seite
ist, dreht sich hier durch eine verstecke Anwendung der Regel von de Morgan das ∧ in ein ∨
um.
Implikation und Disjunktion Die (klassische) aussagenlogische Implikation (A → B) ist
durch ihre Definition per Wahrheitstafel logisch äquivalent zu (¬A ∨ B). Dadurch ergeben
sich einige „Merkwürdigkeiten“: zum einen die sogenannten „Paradoxa der Implikation“, also
die Regeln ex falso quodlibet und verum ex quodlibet, zum andern aber auch Konsequenzen
für die Bi-implikation, die nämlich logisch äquivalent zum verneinten ausschließenden Oder
wird: (A ↔ B) ∼ ¬(A ∨˙ B). Dies bringt zwei eigenständige logische Begriffe in unerwarteten Zusammenhang (der z.B. in der intuitionistischen Aussagenlogik nicht gilt). Da weiterhin
¬(A ∨˙ B) ∼ (¬A ∨˙ B), erhält man die logische Äquivalenz von (A ↔ B) und (¬A ∨˙ B), also
die gleiche Darstellung wie bei der Implikation, aber mit ausschließendem statt einschließendem
Oder. Somit ist der gängige Fehler, Implikation mit Bi-implikation zu verwechseln, derselbe wie
einschließendes mit ausschließendem Oder zu verwechseln.
„Paradoxon der Disjunktion“ ((A → B) ∨˙ (A → ¬B)) ist eine Tautologie; man muß sich
aber vor der irrigen Übersetzung Entweder B folgt logisch aus A oder ¬B folgt logisch aus A
hüten, die im allgemeinen falsch ist. Der Grund ist, daß man hier das Distributivgesetz einmal
richtig, und einmal falsch unter Verschiebung der Bedeutungsebenen verwendet.
Aus ` (A → >), also ` (A → (B ∨˙ ¬B)) folgt mit dem richtig verwendeten Distributivgesetz nämlich, daß ((A → B) ∨˙ (A → ¬B)) eine Tautologie ist. Sprachlich ausgedrückt:
((A → B) ∨˙ (A → ¬B)) ist wahr, d.h. bekommt stets den Wahrheitswert W zugeordnet, da
entweder (A → B) wahr ist, d.h. den Wahrheitswert W bekommt, oder (A → ¬B). Die falsche
Verwendung des Distributivgesetzes, die der irrigen Übersetzung zugrunde liegt, wäre nun, umgekehrt zu schließen: ((A → B) ∨˙ (A → ¬B)) ist eine Tautologie, also ist entweder (A → B)
eine Tautologie oder (A → ¬B). Das syntaktische Oder ∨ verhält sich also distributiv zu „wahr
sein“ im Sinne der Zuordnung des Wahrheitswertes W, nicht aber zu „wahr sein“ im Sinne des
sich auf der übergeordneten Ebene befindlichen „eine Tautologie sein“. Diese Verwechselung
liegt nahe, da man beim Lesen nicht unterscheidet zwischen „(S ∨ T ) ist eine Tautologie“, wofür
das Distributivgesetz nicht gilt, und „S oder T ist eine Tautologie“, was gerade – die natürliche
Sprache benutzt das Distributivgesetz! – „S ist eine Tautologie oder T ist eine Tautologie“ bedeutet. (Ob man hier das ausschließende oder das einschließende Oder versteht, spielt für diese
Problematik keine Rolle.)
Ein einfacheres Beispiel, das daher aber weniger gefährlich ist, weil man es leichter durchschaut,
ist die Tautologie (A ∨ ¬A). Liest man laut „A oder non A ist eine Tautologie“, so dürfte man
bei einem metasprachlichen Oder das Distributivgesetz, das die natürliche Sprache benutzt,
anwenden, und den Satz in „A ist eine Tautologie oder non A ist eine Tautologie“ auflösen. Da
15
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
es sich aber um ein objektsprachliches Oder handelt, darf man dies nicht: aus ` (A ∨ ¬A) folgt
eben nicht ` A oder ` ¬A.
1.4
Junktorensysteme
Die Regel (A → B) ∼ (¬A ∨ B) zeigt, daß man auf den Junktor → auch hätte verzeichten
können; andererseits hätte man auch einen weiteren Junktor ← einführen können mit der Eigenschaft, daß (A ← B) logisch äquivalent zu (B → A) ist. Dieser Abschnitt soll unter anderem
der Frage nachgehen, warum nicht andere Junktoren gewählt wurden und welche Möglichkeiten
es dafür gegeben hätte; zunächst aber aufzeigen, daß keine weiteren Junktoren nötig sind.
1.4.1
Disjunktive und konjunktive Normalform
Ist ein Wahrheitswertverlauf gegeben, so kann man diesen in einer Formel beschreiben. Dazu
gibt es zwei einfache Möglichkeiten: Man arbeitet entweder alle vorkommenden Wahrheitswerte
W ab, oder alle vorkommenden Wahrheitswerte F. Die genauen Verfahren werden im Anschluß
beschrieben: Das erste liefert eine Formel in sogenannter disjunktiver Normalform (DNF), das
zweite in konjunktiver Normalform (KNF). Beide kommen mit den Junktoren ¬, ∧, ∨ sowie
in Extremfällen ⊥ bzw. > aus. Insbesondere wird damit gezeigt sein, daß bis auf logische
Äquivalenz die bisher eingeführten aussagenlogischen Formeln alles ausdrücken können und
keine weiteren Junktoren nötig sind.
Die Verfahren liefern insbesondere zu einer gegebenen aussagenlogischen Formel S logisch äquivalente Formeln in disjunktiver bzw. konjuntiver Normalform. Diese heißen dann auch disjunktive bzw. konjunktive Normalform von S. Beide benutzen nur die in der Ausgangsformel
auftretenden Aussagenvariablen.
Das Verfahren für die disjunktive Normalform
• Für jede Zeile einer Wahrheitstafel kann man eine Formel angeben, welche nur in dieser
Zeile den Wert W annimmt, und sonst stets F. Dazu nimmt man die Aussagenvariablen, die
in dieser Zeile mit W belegt werden, und die Negate der Aussagenvariablen, die in dieser
Zeile mit F belegt werden, und bildet die Konjunktion davon. (Bei n Aussagenvariablen
also eine (n − 1)-fache Konjunktion.)
• Für jede Zeile einer Wahrheitswertverteilung, in welcher W auftritt, nimmt man nun diese
Formeln und bildet die Disjunktion all dieser Formeln: Dies ist die disjunktive Normalform.
Beispiel: Bei drei Aussagenvariablen ist eine Formel S mit der folgenden Wahrheitswertverteilung gesucht
A
W
W
W
W
F
F
F
F
B
W
W
F
F
W
W
F
F
C
W
F
W
F
W
F
W
F
S
F
W
W
F
F
W
F
F
((A ∧ B) ∧ ¬C)
F
W
F
F
F
F
F
F
((A ∧ ¬B) ∧ C)
F
F
W
F
F
F
F
F
((¬A ∧ B) ∧ ¬C)
F
F
F
F
F
W
F
F
Auf der rechten Seite sind die Konjunktionen für den ersten Schritt angegeben. Die Verteilung
der Negationszeichen entspricht dabei genau den Wahrheitswerten der Zeile, in welcher sich W
ergibt: Die Negationszeichen stehen bei den Aussagenvariablen, welche mit F belegt sind, und
16
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
nicht bei den andern. Im zweiten Schritt bildet man nun die Disjunktion dieser Konjunktionen,
also
S = ((A ∧ B) ∧ ¬C) ∨ ((A ∧ ¬B) ∧ C) ∨ ((¬A ∧ B) ∧ ¬C)
Das Verfahren für die konjunktive Normalform Dieses Verfahren arbeitet dual zum
DNF-Verfahren; man vertauscht also überall W mit F und ∧ mit ∨:
• Für jede Zeile einer Wahrheitstafel kann man eine Formel angeben, welche nur in dieser
Zeile den Wert F annimmt, und sonst stets W. Dazu nimmt man die Aussagenvariablen,
die in dieser Zeile mit F belegt werden, und die Negate der Aussagenvariablen, die in dieser
Zeile mit W belegt werden, und bildet die Disjunktion davon. (Bei n Aussagenvariablen
also eine (n − 1)-fache Disjunktion.)
• Für jede Zeile einer Wahrheitswertverteilung, in welcher F auftritt, nimmt man nun diese
Formeln und bildet die Konjunktion all dieser Formeln: dies ist die konjunktive Normalform.
Im obigen Beispiel ergibt sich im ersten Schritt für die zeilenweisen Disjunktionen:
((¬A ∨ ¬B) ∨ ¬C)
F
W
W
W
W
W
W
W
((¬A ∨ B) ∨ C)
W
W
W
F
W
W
W
W
((A ∨ ¬B) ∨ ¬C)
W
W
W
W
F
W
W
W
((A ∨ B) ∨ ¬C)
W
W
W
W
W
W
F
W
((A ∨ B) ∨ C)
W
W
W
W
W
W
W
F
Die Verteilung der Negationszeichen entspricht dabei wieder genau den Wahrheitswerten der
Zeile, in welcher sich F ergibt: Die Negationszeichen stehen bei den Aussagenvariablen, welche
mit W belegt sind, und nicht bei den andern.
Im zweiten Schritt bildet man nun die Konjunktion dieser Disjunktionen, also T =
((¬A ∨ ¬B) ∨ ¬C) ∧ ((¬A ∨ B) ∨ C) ∧ ((A ∨ ¬B) ∨ ¬C) ∧ ((A ∨ B) ∨ ¬C) ∧ ((A ∨ B) ∨ C)
Extremfälle Falls eine Antilogie vorliegt, also die Wahrheitsverteilung nur aus F besteht,
führt das Verfahren für die disjunktive Normalform zu keinen Konjunktionen, die in einer Disjunktion zusammengesetzt werden können. In diesem Fall wird ⊥ als die disjunktive Normalform
gesetzt. Ebenso soll > die konjunktive Normalform einer Tautologie sein.
Außerdem funktioniert das Verfahren nicht, wenn gar keine Aussagenvariablen auftreten. Dann
handelt es sich entweder um eine Tautologie oder um eine Antilogie, und > sei die Normalform
solcher Tautologien und ⊥ die Normalform solcher Antilogien. Dahingegen lassen sich die disjunktive Normalform einer Tautologie mit Aussagenvariablen und die konjunktive Normalform
einer Antilogie mit Aussagenvariablen nach der Methode konstruieren. Die disjunktive Normalform der Tautologie (((A → B)∧A) → B) ist also ((((A∧B)∨(A∧¬B))∨(¬A∧B))∨(¬A∧¬B)).
Beide Normalformen sind nicht eindeutig bestimmt: Weder die Reihenfolge der Aussagenvariablen noch die Reihenfolge der Zeilen der Wahrheitstafel noch die Reihenfolge, in welcher die
Konjunktionen und Disjunktionen gebildet werden, ist festgelegt. Also wäre auch
S 0 = (B ∧ (¬A ∧ ¬C)) ∨ (¬B ∧ (A ∧ C)) ∨ (B ∧ (A ∧ ¬C)
eine disjunktive Normalform für den Satz S. Es ist aber üblich, die Reihenfolge der Aussagenvariablen in jedem Disjunktionsglied beizubehalten.
Arbeitet man viel mit konjunktiven oder disjunktiven Normalformen, sollte man der Übersichtlichkeit halber Regeln einführen, die es gestatten, unnötige Klammern wegzulassen. Dann würde
man z.B. S = ((A ∧ B ∧ ¬C) ∨ (A ∧ ¬B ∧ C) ∨ (¬A ∧ B ∧ ¬C)) schreiben.
17
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Tabelle 1.1: alle zweistelligen Junktoren
A
W
W
F
F
1.4.2
B
W
F
W
F
>
W
W
W
W
∨
W
W
W
F
←
W
W
F
W
A
W
W
F
F
→
W
F
W
W
B
W
F
W
F
↔
W
F
F
W
∧
W
F
F
F
∧|
F
W
W
W
=
F
W
W
F
¬B
F
W
F
W
9
F
W
F
F
¬A
F
F
W
W
8
F
F
W
F
∨|
F
F
F
W
⊥
F
F
F
F
Junktoren
¬ ist ein einstelliger, ∧, ∨, → und ↔ sind zweistellige Junktoren. Allgemeiner ordnet ein nstelliger Junktor jeder der 2n möglichen Verteilungen von n Wahrheitswerten wieder einen
Wahrheitswert zu.4 In diesem Sinne ist zum Beispiel ∧ der Junktor, der W W den Wahrheitswert
W zuordnet, W F sowie F W und F F jeweils den Wahrheitswert F. Ist J ein zum Beispiel
dreistelliger Junktor, so könnte man aus aussagenlogischen Formeln S, T und U eine neue Formel
J(S, T , U) bilden, der in Abhängigkeit von Wahrheitswerten für S, T und U ein Wahrheitswert
gemäß J zugeordnet werden könnte.
0-stellige Junktoren Der Vollständigkeit halber kann man die aussagenlogischen Konstanten
> und ⊥ als 0-stellige Junktoren auffassen; sie geben gewissermaßen einen Wahrheitswert als
Ausgabe auch ohne Eingabe.
1-stellige Junktoren: Es gibt vier einstellige Junktoren: der Junktor, der stets W ausgibt,
der Junktor, der stets F ausgibt, der „Identitäts–Junktor“, der seine Eingabe wieder ausgibt,
und den Negations–Junktor, der W in F und F in W verwandelt. Aus einer Formel A machen
diese Junktoren in gleicher Reihenfolge bis auf logische Äquivalenz die Formeln >, ⊥, A und
¬A. Zusammenfassend als Tabelle:
A
W
F
>
W
W
A
W
F
¬A
F
W
⊥
F
F
Die einstelligen Junktoren sind also in der hier vorgestellten Sprache alle abgedeckt, denn der
„Identitäts–Junktor“ bedarf auf der Formelebene keines Zeichens.
2-stellige Junktoren Es gibt sechzehn zweistellige Junktoren, die in Tabelle 1.1 zusammengefaßt sind. Vier dieser Junktoren sind eigentlich einstellig, da sie nur vom ersten oder nur
vom zweiten Wert abhängen, und zwei eigentlich nullstellig. Sie bekommen in der Tabelle kein
eigenes Zeichen; stattdessen ist die Formal angegeben, die sich ergibt, wenn man aus A und B
mit diesem Junktor eine neue Formel bildet – dies sind A, B, ¬A und ¬B – bzw. > und ⊥.
Für vier der restlichen zehn Junktoren gibt es Zeichen; für die anderen sechs könnte man neue
Zeichen einführen. In der Tabelle ist eine systematische Möglichkeit dazu angegeben: Dabei
zeigt ein Strich durch einen Junktor den negierten Junktor an, also (A 9 B) ∼ ¬(A → B),
(A ∧| B) ∼ ¬(A∧B) usw. Achtung: Diese Zeichen sind nicht Teil der für dieses Skript „offiziellen“
aussagenlogischen Sprache!
Insbesondere ∧| und ∨| sind keine Standardnotationen; üblich ist der Sheffersche Strich (A|B)
anstelle von (A ∧| B); ∨| ist dann der duale Junktor ¬(¬A|¬B), für den es keine übliche Notation
gibt. Die negierte Äquivalenz = funktioniert wie das ausschließende Oder und wird als solches
oft ∨˙ geschrieben.
4 Genauer sind ¬ usw. Zeichen für Junktoren; ebenso ist z.B. die Disjunktion zweier Sätze S und T eigentlich
die Zusammenfassung beider durch den Junktor „Oder“, und (S ∨ T ) nur eine zeichenhafte Darstellung dessen.
18
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Abbildung 1.2: Der Verband der Formeln in zwei Aussagenvariablen A und B
>
P
@PPP
PP
@
PP
@
PP
PP
@
@
P
(A ∨ B)
(A ∨ ¬B)
(¬A ∨ B)
(¬A ∨ ¬B)
`
XX
`X
PP
``` Q
PP
XX
``
QQ
@
@
`
X
P
`
X
XX ``` PP
Q
`
X
PP @
XX ```
XXX ``
QQ
PP@
`
PP
XX ``` Q
@
(A ↔ B)
¬(A ↔ B)
A
¬B
B
¬A
``` XX
PP
Q
X
`
@ PP
``` XX XX
```X
PP QQ
@
XXX PP Q
```
``` XX
@
`XX
Q
PPP
Q
@
``
XX
P
``
@
Q
P
`
(A ∧ B)
(A ∧ ¬B)
(¬A ∧ B)
(¬A ∧ ¬B)
PP
PP
@
@
PP
PP
@
PP @
PP
@
P
⊥
Tabelle 1.2 zeigt noch einmal alle möglichen zweistelligen Junktoren mit den zugehörigen konjunktiven und disjunktiven Normalformen sowie einer Auswahl dazu äquivalenter Formeln. Die
Belegungen sind hier nun vertikal statt wie bislang horizontal notiert.
Bis auf logische Äquivalenz gibt es also genau 16 verschiedene Formeln mit zwei Aussagenvariablen. Diese kann man in einem Diagramm anordnen: siehe Abbildung 1.2. Zunächst sind sie
in Schichten eingeteilt: In der obersten Schicht taucht viermal der Wahrheitswert W auf, in
der zweiten dreimal, und so fort bis zum Falsum in der untersten Schicht. Die geraden Striche
geben an, daß die oben stehende Formel (also die mit mehr Wahrheitswerten W) aus der unten
stehenden logisch folgt: Eine Formel S folgt logisch aus T , wenn man von T anhand von nach
oben laufenden geraden Strichen zu S gelangen kann.
Außerdem ist die Disjunktion zweier Formeln logisch äquivalent zu der „niedersten“ Formel, die
aus beiden folgt, und die Konjunktion zu der „höchsten“, aus der beide folgen. Zum Beispiel
gilt also (A ∨ (A ↔ B)) ∼ (A ∨ ¬B). Die Negation einer Formel S ist logisch äquivalent zu der
einzigen Formel, die sich mit S erst in ⊥ und > „trifft“.
(Die in dem Diagramm dargestellte Struktur wird in der Mathematik ein Boolescher Verband
genannt, hier der von A und B frei erzeugte Boolesche Verband.)
3- und höherstellige Junktoren Diese haben üblicherweise keine besonderen Namen oder
Zeichen. Die disjunktive (oder auch die konjunktive) Normalform zeigt, daß jeder höherstellige
Junktor bereits durch zweistellige Junktoren dargestellt werden kann.
Man beachte: es gibt 2n Möglichkeiten, Verteilungen von n Wahrheitswerten zu erstellen. Hat
man also n Aussagenvariablen in einer Formel, muß man eine Wahrheitstafel mit 2n Zeilen
aufstellen. Für jede dieser Zeilen kann man W oder F auswählen, um einen n-stelligen Junktor
n
zu bilden. Dies bedeutet, daß es 22 viele n-stellige Junktoren gibt: erhöht man die Stelligkeit
um Eins, quadriert sich die Anzahl der Junktoren. Dies sind 256 3-stellige Junktoren, 65 536
4-stellige Junktoren, 4 294 967 296 5-stellige Junktoren...
Dies bedeutet auch, daß es bis auf logische Äquivalenz genau 256 Formeln mit drei festen
Aussagenvariablen gibt, die man ebenso wie die Formeln in zwei Aussagenvariablen in einem
Diagramm wie auf Seite 19 anordnen könnte.
19
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Tabelle 1.2: Tabelle aller zweistelligen Junktoren
Belegung Aussagenvariablen
WW F F
A
WFWF
B
Jkt Verteilung
disjunktive und konjunktive Normalform
äquivalent
> W W W W DNF ((((A ∧ B) ∨ (A ∧ ¬B)) ∨ (¬A ∧ B)) ∨ (¬A ∧ ¬B)) (A ∨ ¬A), ¬(A ∧ ¬A)
KNF >
(A → A), (A ↔ A)
⊥
∨
F F F F DNF ⊥
(A ∧ ¬A), ¬(A ∨ ¬A)
KNF ((((¬A ∨ ¬B) ∧ (¬A ∨ B)) ∧ (A ∨ ¬B)) ∧ (A ∨ B)) (A → ¬A), (A ↔ ¬A)
W W F F DNF ((A ∧ B) ∨ (A ∧ ¬B))
KNF ((A ∨ ¬B) ∧ (A ∨ B))
A, (A ∧ A), (A ∨ A)
(> → A), (> ↔ A)
W F W F DNF ((A ∧ B) ∨ (A ∧ ¬B))
KNF ((¬A ∨ B) ∧ (A ∨ B))
B, (B ∧ B), (B ∨ B)
(> → B), (> ↔ B)
F W F W DNF ((A ∧ ¬B) ∨ (¬A ∧ ¬B))
KNF ((¬A ∨ ¬B) ∧ (A ∨ ¬B))
¬B, (B → ⊥)
F F W W DNF ((¬A ∧ B) ∨ (¬A ∧ ¬B))
KNF ((¬A ∨ ¬B) ∧ (¬A ∨ B))
¬A, (A → ⊥)
W W W F DNF (((A ∧ B) ∨ (A ∧ ¬B)) ∨ (¬A ∧ B))
KNF (A ∨ B)
¬(¬A ∧ ¬B)
← W W F W DNF (((A ∧ B) ∨ (A ∧ ¬B)) ∨ (¬A ∧ ¬B))
KNF (A ∨ ¬B)
(B → A)
¬(¬A ∧ B)
→ W F W W DNF (((A ∧ B) ∨ (¬A ∧ B)) ∨ (¬A ∧ ¬B))
KNF (¬A ∨ B)
¬(A ∧ ¬B)
↔ W F F W DNF ((A ∧ B) ∨ (¬A ∧ ¬B))
KNF ((¬A ∨ B) ∧ (A ∨ ¬B))
((A → B) ∧ (B → A))
¬(A ∨˙ B), (¬A ∨˙ B)
∧
W F F F DNF (A ∧ B)
KNF (((¬A ∨ B)) ∧ (A ∨ ¬B)) ∧ (A ∨ B))
∧|
F W W W DNF (((A ∧ ¬B) ∨ (¬A ∧ B)) ∨ (¬A ∧ ¬B))
KNF (¬A ∨ ¬B)
=
F W W F DNF ((A ∧ ¬B) ∨ (¬A ∧ B))
KNF ((¬A ∨ ¬B) ∧ (A ∨ B))
9
F W F F DNF (A ∧ ¬B)
KNF (((¬A ∨ ¬B) ∧ (A ∨ ¬B)) ∧ (A ∨ B))
¬(A → B)
¬(¬A ∨ B)
8
F F W F DNF (¬A ∧ B)
KNF (((¬A ∨ ¬B) ∧ (¬A ∨ B)) ∧ (A ∨ B))
¬(B → A)
¬(¬B ∨ A)
∨|
F F F W DNF (¬A ∧ ¬B)
KNF (((¬A ∨ ¬B) ∧ (¬A ∨ B)) ∧ (A ∨ ¬B))
¬(¬A ∨ ¬B)
(A → ¬B)
¬(A ∧ B)
(A ∨˙ B)
20
¬(A ∨ B),¬(¬A → B)
¬(¬B → A)
M. Junker „Formale Logik“
1.4.3
Version vom 10. Dezember 2012
Vollständige Junktorensysteme
Eine Auswahl von Junktoren heißt vollständiges Junktorensystem, wenn zu jeder aussagenlogischen Formel eine logisch äquivalente Formel existiert, die nur diese Junktoren benutzt.
Die disjunktive Normalform zeigt, daß ⊥, ¬, ∧, ∨ ein vollständiges Junktorensystem bilden. Nun
kann man ⊥ stets durch (A ∧ ¬A) ersetzen; außerdem gilt mit den de Morganschen Regeln
(A ∧ B) ∼ ¬(¬A ∨ ¬B) und (A ∨ B) ∼ ¬(¬A ∧ ¬B). Damit kann man auch entweder auf ∧
oder auf ∨ verzichten. Mit anderen Worten: ¬, ∧ ist ein vollständiges Junktorensystem, ¬, ∨ ein
anderes.
Ein weiteres vollständiges Junktorensystem ist →, ⊥. Dies gilt, da ¬A ∼ (A → ⊥) und (A∨B) ∼
(¬A → B) ∼ ((A → ⊥) → B).
Kein einstelliger Junktor bildet ein vollständiges Junktorensystem, und es gibt nur zwei zweistellige Junktoren mit dieser Eigenschaft: dies sind ∧| und ∨| . Man sieht nämlich ¬A ∼
(A ∧| A) ∼ (A ∨| A) und (A∧B) ∼ ¬(A ∧| B) ∼ ((A ∧| B) ∧| (A ∧| B)) bzw. (A∨B) ∼ ¬(A ∨| B) ∼
((A ∨| B) ∨| (A ∨| B)).
Warum wurde nun für die Sprache das vollständige Junktorensystem >, ⊥, ¬, ∧, ∨, →, ↔ gewählt und nicht ein kleineres oder ein umfangreicheres? Diese Auswahl der Junktoren unterliegt
einer gewissen Willkür, hat aber historische und systematische Gründe.
Zunächst sollte die Auswahl zweckgerichtet sein: Möchte man z.B. Theoreme über die Aussagenlogik beweisen, ist es geschickt, ein möglichst kleines Junktorensystem zu wählen, da
man dann auch wenige Regeln hat. In der Informatik gibt es die sogenannte Curry–Howard–
Korrespondenz, welche Computerprogramme mit Beweisen in Verbindung setzt. Dort arbeitet
man gerne mit dem Junktorensystem →, ⊥, da diese Junktoren gut den benutzten Konzepten
auf der anderen Seite der Korrespondenz entsprechen.
Wenige Junktoren führen aber zu langen und undurchschaubare Formeln: Ist man an Übersetzungen aus der natürlichen Sprache interessiert, ist es günstiger, viele Junktoren zu wählen,
und zwar solche, die Ausdrücke der natürlichen Sprache wiedergeben. Für eine philosophisch
orientierte formale Logik ist die Auswahl hier günstig, weil die gewählten Junktoren wichtige
logische Konzepte auf dem syntaktischen Ebene widerspiegeln (siehe Tabelle 1.3). Sie bleibt
daher in ihren Ausdrucksmöglichkeiten nahe an der Argumentation in natürlicher Sprache. Außerdem bietet sie dadurch die Chance, auch bei Erweiterungen der Aussagenlogik oder in nichtklassischen Aussagenlogiken Bestand zu haben, in denen etwa die Regel (A → B) ∼ (¬A ∨ B)
nicht gilt und man nicht ohne Verlust → aus dem Junktorensystem entfernen könnte.
Abbildung 1.3: Korrespondenz syntaktische Zeichen – logische Konzepte
Zeichen
>
⊥
¬
∧
∨
→
↔
logisches Konzept
wahr (W), Tautologie
falsch (F), Antilogie
Verneinung
Zusammenfassung einer Menge von Sätzen
Fallunterscheidung
logische Folgerung, Schluß
logische Äquivalenz
Mehr zur Dualität von ∧ und ∨: Warum aber ist das einschließende Oder der „richtige“
Junktor und nicht das ausschließende, wie man meinen könnte?
Ein Grund ist die Dualität von ∧ und ∨, welche auch dazu führt, daß ∨ auf der einen Seite
einer logischen Folgerung die Rolle spielt, welche ∧ auf der anderen einnimmt. Konkret:
((S → T1 ) ∧ (S → T2 )) ∼ (S → (T1 ∧ T2 ))
((S1 → T ) ∧ (S2 → T )) ∼ ((S1 ∨ S2 ) → T )
21
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Oder als Schlußregeln (wobei diese in beide Richtungen, also auch von unten nach oben, gelesen
werden können):
S1
S2
`
`
T
T
S
S
`
`
T1
T2
(S1 ∨ S2 )
`
T
S
`
(T1 ∧ T2 )
Andererseits entspricht ein ∧ auf der linken Seite der Zusammenfassung einer Prämissenmenge:
in Σ ` T kann man eine endliche Menge Σ, etwa aus S1 , S2 bestehend, durch die Konjunktion
ihrer Elemente ersetzen. Das Dualitätsprinzip besagt dann, daß eine Menge von Konklusionen
auf der rechten Seite als Disjunktion aufzufassen wäre, was man durch Anwendung der Kontraposition auch nachrechnen kann: aus S1 , S2 ` T erhält man ¬T ` (¬S1 ∨ ¬S2 ). Also kann man
ergänzend auch die Regeln
S1 , S2
`
T
S
`
T 1 , T2
(S1 ∧ S2 )
`
T
S
`
(T1 ∨ T2 )
aufstellen. In beiden Fällen handelt es sich jedenfalls um ein einschließendes Oder, womit nachgewiesen ist, daß dies ein natürlicher Junktor ist.
Im Gegensatz dazu ist auf den zweiten Blick das hinter dem ausschließenden Oder stehende
logische Konzept gar nicht so klar ist, wie man zunächst meinen könnte. In nicht-klassischen
Logiken, z.B. im Intuitionismus, sind die beiden Formeln ((A ∧ ¬B) ∨ (¬A ∧ B)) und ((A ∨ B) ∧
¬(A ∧ B)) nicht mehr logisch äquivalent. Dies mag als ein Grund dienen, für das ausschließende
Oder kein primitives Zeichen zu wählen. Zudem kann man in Situationen, in denen man im Alltag ein ausschließendes Oder verwendet, oft bemerken, daß man ebensogut ein einschließendes
Oder hätte setzen können, weil die Ausschließlichkeit gar kein substantieller Teil der Aussage
ist, sondern sich aus Zusatzwissen über das Modell, in dem wir uns bewegen, ergibt.
1.5
1.5.1
Alternative Zugänge
Methoden zum Testen von Erfüllbarkeit
Alle aussagenlogischen Fragen lassen sich auf Fragen der Erfüllbarkeit zurückführen. Zum Beispiel ist eine Formel genau dann eine Tautologie, wenn ihre Negation nicht erfüllbar ist. Man
unterscheidet in der Regel drei Fragestellungen:
1) Das Entscheidungsproblem: Ist eine Formel erfüllbar oder nicht?
2) Das Konstruktionsproblem: Man finde zu einer Formel eine erfüllende Belegung.
3) Das Auflistungsproblem: Man finde zu einer Formel alle erfüllenden Belegungen.
Mit dem Erstellen von Wahrheitstafeln hat man eine Methode zur Hand, welche es gestattet,
alle diese Fragen zu entscheiden. Allerdings handelt es sich schon beim Entscheidungsproblem
um ein sogenanntes NP-vollständiges Problem, d.h. das Verfahren dauert in der Regel (bei
großen Formeln) zu lange, um praktikabel zu sein. Dagegen geht es schnell zu entscheiden, ob
eine Formel unter einer gegebenen Belegung erfüllbar ist.
Für die allgemeinen Probleme gibt es im wesentlichen keine anderen Verfahren, als die Wahrheitstafeln zu konstruieren. Es gibt aber viele verschiedene Arten, dies zu organisieren und
aufzuschreiben, von denen manche geschickter und weniger aufwendig sind, als die gesamte
Wahrheitstafel aufzuschreiben.
Bei bestimmten, einfachen Formeln, gibt es aber schnellere Verfahren. Dies wurde genau untersucht und man kennt genau die Arten von Formeln, welche schnellere Verfahren erlauben.
Das Entscheidungsproblem läßt sich nicht schneller lösen als das Konstruktionsproblem: die
22
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Verfahren, die man kennt, konstruieren auch immer eine erfüllende Belegung. Dagegen braucht
das Auflistungsproblem mehr Zeit, allein deshalb, weil es so lange dauert, alle erfüllenden Belegungen niederzuschreiben. In einem technischen Sinn ist dies aber der einzige Grund (bis auf
wenige merkwürdige Ausnahmen für spezielle Formeln, für die es schnelle Entscheidungs–, aber
keine schnellen Auflistungsverfahren gibt).
Als Beispiel für solch eine einfache Formel mit schnellem Verfahren kann man eine der Form
(A ∨ S) betrachten. Sie ist stets erfüllbar, was man sofort sieht, auch wenn S sehr lang und
kompliziert ist, und jede Belegung, welche A mit W belegt, ist erfüllend. Allerdings sieht man
so noch nicht notwendig alle erfüllenden Belegungen! Es lohnt sich auf jeden Fall, eine Formel
zunächst genauer anzuschauen, bevor man blind ein Verfahren anwendet, welches sich anschickt,
die ganze Wahrheitstafel auszurechnen.
Im Rest des Abschnittes werden nun einige Arten vorgestellt, wie man das Erstellen der Wahrheitstafel organisieren kann. Allerdings hat jede Methode ihre Vor– und Nachteile, und keine
funktioniert in jedem Fall besser als eine andere.
Wahrheitstafeln „vertikal“ Dies ist die bisherige Methode, Wahrheitstafeln Junktor um
Junktor für alle Belegungen gleichzeitig abzuarbeiten. Vorteil: braucht in der kondensierten
Version wenig Platz. Nachteil: dauert lange; stets muß die gesamte Wahrheitstafel abgearbeitet
werden.
Wahrheitstafeln „horizontal“ Man kann die Wahrheitstafel auch Belegung um Belegung
auswerten. Zusätzlicher Vorteil: Man kann aufhören, wenn eine Belegung W liefert, falls man auf
Erfüllbarkeit testet, bzw. wenn eine Belegung F liefert, falls man auf Tautologie prüft. Nachteil:
man muß sich stets neu überlegen, wie der Junktor funktioniert, falls man dies nicht auswendig
weiß.
Formeln von „oben“ auswerten, Tableau-Methode Statt mit den Belegungen anzufangen, kann man auch vom Ergebnis her argumentieren: Man schaut sich im Formelaufbau den
letzten hinzugekommenen Junktor an und bestimmt, welche Wahrheitswertverteilungen der dadurch verbundenen Teilformeln den Wert W liefern, und arbeitet sich so nach unten. Vorteil:
liefert manchmal sehr schnell ein Ergebnis (wie in dem Beispiel (A ∨ S) oben). Nachteil: man
verliert schnell den Überblick.
Es gibt verschiedene Varianten dieser Idee unter dem Namen Tableau-Methode oder Baumkalkül.
Umformung in Normalform Man ersetzt zunächst alle Junktoren → und ↔ durch logisch
äquivalente Ausdrücke in ¬, ∧ und ∨ und formt dann unter Verwendung der Regeln von de Morgan und der logischen Gesetze für diese Junktoren in disjunktive oder konjunktive Normalform
um (siehe Abschnitt 1.4.1). Die Formel ist erfüllbar, falls die konjunktive Normalform nicht
⊥ ist, und eine Tautologie, falls die disjunktive Normalform > ist. Nachteil: sehr aufwendig.
Vorteil: bietet sich für manche Formeln an, die bereits nahe an einer Normalform sind.
Für Formeln, die bereits in Normalform sind, kann man die meisten Fragen ganz schnell entscheiden, da man der Normalform den Wahrheitswertverlauf der Formel einfach ablesen kann.
Heuristische Methoden Man rät eine erfüllende Belegung und rechnet für diese eine Belegung den Wahrheitswert der Formel aus. Vorteil: ist bei kurzen oder überschaubaren Formeln oft
die schnellste Variante. Nachteil: unsystematisch und damit unübersichtlich, falls kein schneller
Erfolg gegeben ist. Funktioniert nur bei positiver Antwort auf die Frage nach Erfüllbarkeit und
negativer Antwort auf die Frage nach Tautologie. Vom komplexitätstheoretischen Standpunkt
her ist dieses Verfahren übrigens ebenso gut wie andere.
Ebenfalls eine sinnvolle heuristische Herangehensweise ist das Vereinfachen einer Formel durch
logische Umformungen, etwa das Weglassen von Doppelnegationen. Dies kann man auch zu
einer formalen Methode ausbauen, siehe Abschnitt 1.5.3.
23
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Abbildung 1.4: Ein Beispiel für die Methode von Quine
(¬((¬A ∨ B) ∧ ¬¬B) ∨ (A ∧ ¬⊥))
A: W
(¬((¬> ∨ B) ∧ ¬¬B) ∨ (> ∧ ¬⊥))
∼ >
A: F
(¬((¬⊥ ∨ B) ∧ ¬¬B) ∨ (⊥ ∧ ¬⊥))
∼ ¬¬¬B
W
B: W
B: F
¬¬¬>
∼ ⊥
¬¬¬⊥
∼ >
F
W
In der Praxis wird eine Mischung aller Methoden das sinnvollste sein: zunächst ins Auge springende logische Vereinfachungen durchführen, dann eventuell eine Belegung raten, und/oder je
nach Form der Formel eine der systematischen Methoden anwenden. Eine der besten ist:
Die Methode von Quine Sie arbeitet Aussagenvariable um Aussagenvariable ab. Belegungen werden zunächst für eine Variable festgelegt, und die Formel daraufhin vereinfacht. Man
betrachtet also auf der einen Seite Belegungen, welche einer ausgewählten Aussagenvariablen,
etwa B, den Wahrheitswert W zuordnen, und kann dann B durch das Verum > ersetzen; auf
der anderen Seite Belegungen, welche derselben Aussagenvariablen F zuordnen, weswegen man
sie durch ⊥ ersetzen kann. Dann vereinfacht man die Formel anhand der nachfolgenden Rechenregeln für Verum und Falsum. Anschließend fährt man mit den verbleibenden beiden Formeln
fort. Günstig ist es, stets mit der am häufigsten auftretenden Aussagenvariablen zu beginnen.
Ein Beispiel findet sich in Abbildung 1.4.
Vorteil: ist oft sehr schnell. Nachteil: man braucht viel Platz „in der Breite“; die Vereinfachungen
sind langwierig, wenn man sie systematisch Schritt um Schritt durchführt.
Rechenregeln für > und ⊥:
¬>
(A ∧ >)
(A ∨ >)
(A ↔ >)
(A → >)
(> → A)
∼
∼
∼
∼
∼
∼
⊥
(> ∧ A) ∼ A
(> ∨ A) ∼ >
(> ↔ A) ∼ A
>
A
¬⊥
(A ∧ ⊥)
(A ∨ ⊥)
(A ↔ ⊥)
(A → ⊥)
(⊥ → A)
∼
∼
∼
∼
∼
∼
>
(⊥ ∧ A) ∼ ⊥
(⊥ ∨ A) ∼ A
(⊥ ↔ A) ∼ ¬A
¬A
>
Vennsche Diagramme Die Wahrheitswertverläufe von Formeln (mit wenigen Aussagenvariablen) kann man sich auch geometrisch in den sogenannten Vennschen Diagrammen herleiten.
Dazu malt man zu jeder vorkommenden Aussagenvariable einen Kreis, wobei das Innere des
Kreises gedanklich die Belegungen oder Modelle umfassen soll, in welchen diese Aussagenvariable mit W belegt ist, das Äußere des Kreises die andern. Die verschiedenen Kreise müssen
so gezeichnet sein, daß alle Möglichkeiten für einen Punkt, innerhalb gewisser und außerhalb
anderer Kreise zu liegen, auftreten. Bei n Aussagenvariablen müssen also 2n kleinste Gebiete
entstehen, die dann genau den Belegungen entsprechen. Dies geht bis n = 3 sehr gut, bei n = 4
passabel, ab 5 wird es unübersichtlich.
Nun kann man jeder Formel einen Bereich zuordnen (der den erfüllenden Belegungen entspricht): Für die Aussagenvariablen ist das gerade durch die Konstruktion geschehen. Dem
Verum wird das Gesamtgebiet, dem Falsum die leere Menge zugeordnet. Die Junktoren entsprechen nun mengentheoretischen Operationen: Negation der Komplementbildung, Konjunktion dem Schnitt und Disjunktion der Vereinigung. Die Implikation (S → T ) ersetzt man am
24
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
besten durch (¬S ∨T ); sie steht in Verbindung mit der Teilmengenbeziehung. Die Bi-implikation
nimmt zum Schnitt noch das gemeinsame Äußere (d.h. die Schnitte der Komplemente) hinzu.
Eine arithmetische Methode Die folgende Methode hat wenig praktischen Nutzen, sondern
sei nur interessehalber aufgeführt. Wenn oben öfters vom „Ausrechnen“ von Wahrheitswerten
die Rede war, so kann man dies tatsächlich auch mit üblichen Rechenoperationen tun. Dazu
identifiziert man den Wahrheitswert W mit der Zahl 1 und F mit 0. Möchte man den Wert
einer Formel unter einer Belegung errechnen, so setzt man alle Aussagenvariablen, welchen
die Belegung den Wahrheitswert W zuordnet, gleich 1, ebenso das Verum, und alle anderen
Aussagenvariablen wie auch das Falsum gleich 0. Die Junktoren berechnen sich dann wie folgt:
¬S
(S ∧ T )
(S ∨ T )
(S → T )
(S ↔ T )
als
als
als
als
als
1−S
S ·T
S +T −S ·T
1−S +S ·T
1 − (S − T )2
Man beachte, daß als Ergebnis stets wieder 0 oder 1
herauskommt, wenn man nur 0 und 1 hineingibt, und
daß die Operationen das gewünschte Ergebnis liefern!
Beispielsweise übersetzt sich der Satz (¬((¬A ∨ B) ∧ ¬¬B) ∨ (A ∧ ¬⊥)) in den arithmetischen
Ausdruck 1 − ((1 − A + B − (1 − A) · B) · (1 − (1 − B))) + (A · (1 − 0)) − (1 − ((1 − A + B −
(1 − A) · B) · (1 − (1 − B)))) · (A · (1 − 0)). Unter der Belegung A: F, B: W ergibt sich also
1 − ((1 − 0 + 1 − (1 − 0) · 1) · (1 − (1 − 1))) + (0 · (1 − 0)) − (1 − ((1 − 0 + 1 − (1 − 0) · 1) · (1 −
(1 − 1)))) · (0 · (1 − 0)) = 0.
1.5.2
Einige traditionelle Schlußregeln
Traditionell hat man logische Gesetze nicht als Tautologien oder logische Äquivalenzen beschrieben, sondern durch Schlußweisen, die meist in der Form
Prämisse 1
..
.
Prämisse n
Konklusion
notiert werden. Ein solcher Schluß (genauer die Schlußweise, also die Argumentation) heißt
korrekt (engl. valid ), falls die aussagenlogische Entsprechung
(· · · (Prämisse 1 ∧ Prämisse 2) ∧ · · · ∧ Prämisse n) → Konklusion
eine Tautologie ist. Der Schluß heißt sound, falls er nicht nur korrekt ist, sondern auch die Prämissen (in dem betrachteten Kontext) gelten bzw. wahr sind. Während die englischen Bezeichnungen valid und sound in dieser Bedeutung verbreitet und standardisiert sind, gilt dies nicht
für vorgeschlagene deutsche Übersetzungen. Bisweilen liest man gültig für valid und schlüssig
für sound, bisweilen aber auch andere Wörter oder sogar den umgekehrten Gebrauch.
Hier folgen nun einige korrekte Schlußweisen, die im Mittelalter betrachtet wurden und mit
Namen versehen, sowie einige der häufigsten Fehlschlüsse, also nicht korrekte und daher zu
vermeidende Schlußweisen. Die Listen sind natürlich nicht vollständig; vor allem nicht die Liste
der zu vermeidenden Fehlschlüsse! Wichtig ist der erste Teil bis zur gestrichelten Linie.
Modus ponens
Modus tollens
Kontraposition
Σ ` (A → B)
Σ`A
Σ ` (A → B)
Σ ` ¬B
Σ ` (A → B)
Σ`B
Σ ` ¬A
Σ ` (¬B → ¬A)
Σ ` (A ↔ B)
Σ ` (¬B ↔ ¬A)
25
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
nicht korrekt:
nicht korrekt:
nicht korrekt:
Σ ` (A → B)
Σ`B
Σ ` (A → B)
Σ ` ¬A
Σ ` (A → B)
Σ`A
Σ ` ¬B
Σ ` (B → A)
Σ ` (A → B)
Σ ` (¬A → ¬B)
.............................................................................................
Satz des Duns Scotus
(Paradoxa der Implikation)
Satz des Petrus Hispanus
Σ ` (A ∧ B)
Σ ` ¬A
Indirekter Beweis
(reductio ad absurdum)
Σ, A
`⊥
Σ ` (A → B)
Σ`A
Σ`B
Σ`A
Σ ` (A → ¬A)
Σ ` (A → B)
Σ ` (A ∨ B)
Σ ` ¬A
konstruktives Dilemma
Σ ` (A ∨ B)
Σ ` (A → C)
Σ ` (B → D)
Σ ` (C ∨ D)
einfacher Syllogismus
Σ
Fallunterscheidung
Σ ` (A ∨ B)
Σ ` (A → C)
Σ ` (B → C)
Σ`C
disjunktiver Syllogismus
Σ ` (A → B)
Σ ` (B → C)
Σ ` (A ∨ B)
Σ ` ¬B
Σ ` (A → C)
Σ`A
1.5.3
` ¬A
Satz des Clavius
destruktives Dilemma
Σ ` (A → C)
Σ ` (B → D)
Σ ` (¬C ∨ ¬D)
Σ ` (¬A ∨ ¬B)
nicht korrekt:
Σ ` (A ∨ B)
Σ`A
Σ ` ¬B
Beweiskalküle
Bislang wurde der Folgerungsbegriff semantisch bestimmt: S folgt logisch aus Σ, wenn in allen
möglichen Modellen, d.h. unter allen möglichen Interpretationen, die Σ wahr machen, auch S
wahr wird. Diese Vorgehensweise hat mehrere Nachteile:
(1) Sie ist weit entfernt von der üblichen Art und Weise zu argumentieren und unhistorisch.
(2) Sie ist oft praktisch nicht durchführbar, etwa wenn man unendliche Formelmengen betrachtet, oder bei komplizierteren logischen Systemen, wo man vielleicht keinen Überblick über die
möglichen Modelle hat oder man nicht mehr einfach auswerten kann, ob ein Satz in einem Modell gilt oder nicht.
(3) Es könnte sein, daß man lieber eine nicht-klassische Logik erstellen möchte, die näher am
natürliche Argumentieren liegt, aber sich nicht durch Modellbeziehungen beschreiben läßt.
Daneben gibt es die Möglichkeit, den Folgerungsbegriff syntaktisch zu bestimmen. Dazu stellt
man ein Regelwerk auf, das bestimmt, welche Formeln logisch aus einer Formelmenge folgen
(sogenannte Axiome), und wie man aus Formeln, von denen man bereits weiß, daß sie logisch
aus einer Formelmenge folgen, neue solche Formeln gewinnt (sogenannte Folgerungsregeln oder
einfach Regeln). Ein solches Regelwerk nennt man auch einen Beweiskalkül. Ein Beweiskalkül
besteht also aus einer Menge von Schlußweisen, die man als gültig akzeptiert. Man sieht, daß
man, falls man mit der klassischen Logik nicht glücklich ist, einen Beweiskalkül leichter abändern
kann, indem man zweifelhafte Schlußweisen entfernt oder durch akzeptierte Abschwächungen
ersetzt.
Von jedem Beweiskalkül (für die klassische Aussagenlogik) muß man zeigen, daß er wunschgemäß arbeitet, also zum einen die Korrektheit des Kalküls: Wenn der Beweiskalkül eine logische
26
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Folgerung aufzeigt, so soll sie auch gelten (d.h. mit Wahrheitswerten nachprüfbar sein); zum
anderen die Vollständigkeit des Kalküls: alles, was logisch folgt, soll auch mit dem Beweiskalkül gefunden werden können. Die Korrektheit ist in allen Fällen hier leicht einzusehen; die
Vollständigkeit ist schwieriger und wird hier nicht gezeigt werden.
Gentzen– oder Regelkalküle bestehen aus einem Axiom und vielen Regeln; Hilbert– oder Axiomenkalküle bestehen aus vielen Axiomen und einer Regel, dem Modus ponens.
Die Axiome und Regeln funktionieren folgendermaßen: über dem Strich stehen logische Folgerungen, die man bereits aus dem Kalkül abgeleitet hat. Ihre Reihenfolge spielt keine Rolle.
Im Falle der Axiome braucht man keine vorherigen Ableitungen: es steht also nichts über dem
Strich. Unter dem Strich steht dann eine neue erlaubte Folgerung.
Ein Beweis oder Ableitung in einem Kalkül ist nun eine Reihe von Folgerungen Σ ` S, die
entweder Axiome des Kalküls sind oder sich aus weiter vorne in der Reihe stehenden Folgerungen
durch Anwenden einer Regel des Kalküls ergibt.
Ein Gentzen–Kalkül Dieser Kalkül arbeitet nur mit den Junktoren ¬ und ∨. Entweder man
versteht die anderen Junktoren als Abkürzungen, oder man muß den Kalkül um weitere Regeln
für die anderen Junktoren erweitern.
Axiom:
Σ`S
falls der Satz S in der Satzmenge Σ enthalten ist.
Regeln:
Monotonieregel:
Fallunterscheidungsregel:
∨-Einführung links:
Σ `S
Σ0 ` S
Σ, T ` S
Σ, ¬T ` S
Σ
`S
Σ, S
`T
Σ, S 0
`T
Σ, (S ∨ S 0 ) ` T
falls Σ in Σ0 enthalten, d.h. jeder
Satz aus Σ auch in Σ0 vorkommt.
Widerspruchsregel:
Σ, ¬S ` T
Σ, ¬S ` ¬T
Σ
`S
∨-Einführung rechts:
Σ`S
Σ ` (S ∨ T )
Σ`S
Σ ` (T ∨ S)
Die Korrektheit des Kalküls überprüft man leicht; die Vollständigkeit ist dagegen immer schwer
und langwierig zu beweisen (einen Beweis findet man z.B. im Buch von Ebbinghaus, Flum,
Thomas).
Beispiel einer Ableitung:
1)
2)
3)
4)
5)
A,
A,
A,
A,
A
¬A, ¬¬¬A ` A
¬A, ¬¬¬A ` ¬A
¬A
` ¬¬A
¬¬A
` ¬¬A
` ¬¬A
Axiom
Axiom
Widerspruchsregel auf 1) und 2)
Axiom
Fallunterscheidung auf 3) und 4)
Ein Hilbert–Kalkül Diese Version eines Hilbert–Kalküls arbeitet mit dem vollständigen
Junktorensystem ¬ und →. Dem Vorteil der wenigen Axiome steht der Nachteil inintuitiver
Regeln und umständlicher Beweise entgegen.
Regel:
Modus Ponens
Σ`S
Σ ` (S → T )
Σ`T
27
M. Junker „Formale Logik“
Axiome:
2)
1)
Σ`S
Version vom 10. Dezember 2012
falls S in Σ vorkommt.
Σ ` (S → (T → S))
3)
Σ ` ((¬S → ¬T ) → ((¬S → T ) → S))
4)
Σ ` ((S → (T → U)) → ((S → T ) → (S → U)))
Beispiel einer Ableitung:
1)
2)
3)
4)
5)
6)
7)
(A → B),
(A → B),
(A → B),
(A → B),
(A → B),
(A → B),
(A → B),
1.6
(B
(B
(B
(B
(B
(B
(B
→ C)
→ C)
→ C)
→ C)
→ C)
→ C)
→ C)
`
`
`
`
`
`
`
(A → B)
(B → C)
((B → C) → (A → (B → C)))
(A → (B → C))
((A → (B → C)) → ((A → B) → (A → C)))
((A → B) → (A → C))
(A → C)
Axiom 1
Axiom 1
Axiom 2
Modus Ponens 2), 3)
Axiom 4
Modus Ponens 4), 5)
Modus Ponens 1), 6)
Übersetzungen
Wie schon in der Einleitung ausgeführt, ist die Aussagenlogik eine in sich geschlossene Theorie,
über deren Anwendbarkeit man im Einzelnen nachdenken muß. Da diese „ideale“ Theorie aber
einen Abstraktionsprozeß aus dem Wahrheitswertverhalten tatsächlich benutzter Sätze erwachsen sein dürfte, ist diese Anwendbarkeit prinizpiell gegeben. Dies bedeutet: Hinter einem Text,
einer Argumentation usw. steht in der Regel eine logische Struktur, für die es eine (mehr oder
minder aussagekräftige) aussagenlogische Annäherung gibt. Es folgen in diesem Abschnitt ein
paar Anmerkungen über die Problematik, diese Struktur herauszuarbeiten.
Dieser Abstraktionsprozeß, also der Versuch, natürliche Sprache in aussagenlogischen Formeln
wiederzugeben, ist die Umgekehrung des Übersetzungsprozesses, den man bei der Konstruktion von Modellen und Interpretationen in Abschnitt 1.2.2 liefert. Dieser ist vergleichsweise
unproblematisch; allerdings muß man im Auge behalten, bei der sprachlichen Wiedergabe der
Junktoren nicht mehr in diese hineinzulegen als allein ihre logische Struktur.
Bei der Wiedergabe natürlicher Sprache in Aussagenlogik muß man folgende Punkte beachten:
• Viele Arten von Zusammenhängen zwischen Sätzen sind in Aussagenlogik nicht ausdrückbar (etwa kausale oder temporale Abhängigkeiten).
• Natürliche Sprache ist vieldeutig und Interpretationen unterworfen, auch bei der logischen
Struktur (beispielsweise ist oft unklar, ob ein Oder ein– oder ausschließend gemeint ist).
• Logische Konzepte, die in aussagenlogischen Junktoren festgehalten sind, entsprechen
nicht unbedingt dem Alltagsgebrauch dieser Konzepte (vergleiche z.B. Verneinung, Gegenteil, Gegensatz).
• Der Name eines logischen Junktors hat in der natürlichen Sprache meist mehrere oder
andere Bedeutungen.
Die folgenden Anmerkungen liefern nur einen kleinen Ausschnitt dessen, was man zu Übersetzungsfragen sagen könnte. Viele sprachliche Wendungen, hinter denen aussagenlogische Junktoren stecken, sind nicht aufgeführt. Und da Übersetzungen immer auch Interpretationen sind,
kann man bei manchen Beispielen durchaus anderer Auffassung sein als ich.
28
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Anmerkungen zur Negation Eine logische gültige Verneinung einer Aussage erhält man
stets durch Voranstellen einer Formulierung wie „Es ist nicht der Fall, daß ...“, was aber sprachlich meist unbefriedigend ist und selten vorkommt. Häufig erfolgt eine Verneinung durch ein
Verneinungswort wie „nicht“, „kein“; in diesem Fall muß man aber genau prüfen, ob die gesamte
Aussage verneint wird oder nur ein Satzteil. Außerdem muß man beachten, daß bisweilen ein
zweites Verneinungswort verstärkend anstatt aufhebend hinzutritt.
Verneinungen können auch semantisch gebildet werden; dann ist allerdings große Vorsicht geboten, da oft das formal bestimmte „Gegenteil“ mit einem inhaltlich entgegengesetzten „Gegensatz“
verwechselt wird. In diesem Sinne des (nicht allgemeinen gültigen) Gebrauchs von „Gegenteil“
und „Gegensatz“ wäre heiß ein Gegensatz zu kalt, das Gegenteil dagegen nicht kalt. Mithin ist
„Das Wasser ist heiß“ keine gültige logische Verneinung von „Das Wasser ist kalt“. Im Alltag
funktionieren solche ungenauen Verneinungen dennoch oft, wenn der Zwischenbereich implizit
ausgeschlossen ist.
Um korrekte semantische Veneinungen bilden zu können, braucht man Zusatzinformation: Nur
dann ist „Azolla ist polypodial“ eine gültige Verneinung von „Azolla ist monopodial“, wenn „polypodial“ als “nicht monopodial“ definiert ist, d.h. es keine andere Möglichkeit für Azolla gibt, als
mono– oder polypodial zu sein. So wird man „Sokrates ist eine Frau“ vor dem Hintergrund des
Wissens, daß Sokrates ein Mensch ist, als Verneinung von „Sokrates ist ein Mann“ akzeptieren,
nicht aber, falls mit „Sokrates“ der Name eines studentischen Austauschprogramms gemeint ist.
Anmerkungen zur Konjunktion Die Konjunktion kann sprachlich durch und wiedergegeben werden, es gibt aber viele andere Möglichkeiten (sowie, auch...; parataktisch oder als
Relativsatz). Nicht jedes und fungiert als logischer Junktor, etwa in dem Satz „Männer und
Frauen sind gleichberechtigt“ faßt das und nicht zwei Aussagen zu einer zusammen. Den ähnlich aussehenden Satz „Männer und Frauen sind wahlberechtigt“ kann man dagegen auflösen in
„Männer sind wahlberechtigt und Frauen sind wahlberechtigt“.
Oft verbindet ein und zwei Teilsätze nicht nur im Sinne der logischen Konjunktion, sondern
auch in konsekutiver, kausaler, konzessiver o.a. Hinsicht. Dies führt manchmal dazu, daß es
nicht mehr kommutativ ist: Die Sätze „Ich war hungrig und habe in der Mensa gegessen“ und
„Ich habe in der Mensa gegessen und war hungrig“ haben einen verschiedenen Sinn.
Anmerkungen zur Disjunktion Die Disjunktion wird sprachlich meist durch oder wiedergegeben. Allerdings kann oder sowohl für das einschließende Oder ∨ (lateinisch vel ... vel )
als auch für das ausschließende Oder ∨˙ (lateinisch aut ... aut) stehen. Hier besteht eine große
Fehler– und Irrtumsquelle! Ein logisches Oder kann auch hinter anderen sprachlichen Konstruktionen stehen, beispielsweise kann es sei denn, daß ... ein ausschließendes Oder bedeuten.
Andererseits muß nicht jedes sprachliche oder die Rolle eines logischen Junktors übernehmen.
Beispielsweis kann man „Sein oder Nichtsein[, das] ist hier die Frage“ kaum in „Sein ist hier die
Frage oder Nichtsein ist hier die Frage“ auflösen. Allerdings ist es kein wirklich befriedigendes
Beispiel, da der Satz korrekter „‚Sein oder Nichtsein‘, das ist hier die Frage“ lauten müßte.
Ein anderes Beispiel findet sich bei Husserl: „[...] nicht jedes richtige Urteil [...] ist ein Wissen
vom Sein oder Nichtsein dieses Sachverhalts.“ Auch den obigen Beispielsatz eines und, welches
nicht für eine aussagenlogische Konjunktion steht, kann man merkwürdigerweise auch mit einer Wendung ausdrücken, welche oder benutzt: „Alle Menschen sind gleichberechtigt, seien sie
Männer oder Frauen.“ 5
Es gibt eine vermutlich eine Tendenz, ein oder zunächst eher ausschließend aufzufassen, also als
eine echte Fallunterscheidung. Dies mag daran liegen, daß in vielen Fällen der einschließende Fall
gar nicht logisch ausgeschlossen ist, sondern durch Zusatzwissen oder –annahmen. Bei „Heute
abend gehe ich ins Kino oder Theater“ faßt man das oder ausschließend auf, da man davon
ausgeht, daß man den Abend nur mit einer Veranstaltung gestaltet.
Will man betonen, daß es sich um ein einschließendes Oder handelt, muß man den dritten Fall
gesondert aufführen: „Heute abend gehe ich ins Kino oder Theater oder mache beides“. Mit
5 Mitgeteilt
von Olivier Roche.
29
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Entweder ... oder kann man betonen, daß es sich um ein ausschließendes Oder handelt. Da im
Deutschen eine Konstruktion wie oder ... oder fehlt, die es in vielen Sprachen gibt, benutzt man
allerdings manchmal entweder ... oder, um darauf aufmerksam zu machen, daß die Auflistung
zweier oder mehrerer Fälle folgt, wobei diese sich nicht notwendig ausschließen müssen.
Anmerkungen zu den de Morganschen Regeln Die Regeln von de Morgan bieten in
der „Alltagslogik“ gewisse Schwierigkeiten, die zum Teil auch auf sprachlichen Ungenauigkeiten
beruhen. Ein strenger Vegetarier müßte logisch korrekt sein Essen als „nicht mit Fleisch oder
mit Fisch“ bestellen; der Variante „nicht mit Fleisch und mit Fisch“ dürfte man aber auch
manchmal begegnen (wobei das weitere Problem auftritt, daß sich das nicht nur auf den ersten
Teil beziehen könnte.) Sprachlich eleganter ist freilich „weder mit Fleisch noch mit Fisch“ –
weder ... noch ... entspricht dem Junktor ∨| .
Auch die Unklarheit zwischen ausschließendem und einschließendem Oder birgt Schwierigkeiten:
Wird man gefragt, ob man am Abend ins Kino oder ins Theater gehen möchte, und verneint dies,
wird man kaum glücklich sein, wenn der Fragende Karten für beides besorgt. Wie oben erläutert,
liegen die Umstände, welche einen dieses oder ausschließend auffassen lassen, außerhalb des
Bereichs der Fragestellung.
Die duale Regel, also die Verneinung einer Konjunktion, tritt im Alltag seltener auf, da man
üblicherweise angibt, welches Konjunktionsglied man verneint wissen möchte: Wenn man nicht
Zucker und Milch möchte, liegt es in der Regel entweder daran, daß man keinen Zucker, oder
daran, daß man keine Milch möchte. Daran liegt es wohl auch, daß es keine prägnante zu weder
... noch ... duale Formulierung, also für den Junktor ∧| , gibt. Man muß sich mit Konstruktionen
wie „nicht gleichzeitig A und B“ behelfen. Auch kann es sei denn, daß ... die Rolle dieses
Junktors übernehmen, wenn es nicht als ausschließendes Oder aufgefaßt wird.
Kommas können sowohl für eine Konjunktion als auch für eine Disjunktion stehen, ersteres etwa
im Satz „Ich gehe gerne ins Kino, ins Theater, ins Konzert“, letzteres etwa in der Frage „Gehn
wir morgen ins Kino, ins Theater, ins Konzert? “. Eine Verneinung vertauscht hier wegen der
Regeln von de Morgan und und oder : In „Ich gehe ungern ins Kino, ins Theater, ins Konzert“
müßte man die Kommas korrekterweise als Disjunktion auffassen.
Ein scheinbar falscher de Morgan tritt auf, wenn ein und zwei Teile zu einer festen Einheit
verbindet, so wahrscheinlich in dem folgenden Beispiel. Oder kannte Aristoteles die Regeln von
de Morgan nicht?6
Als ungerecht gilt, wer die Gesetze, wer die gleichmäßige Verteilung der Güter, die
bürgerliche Gleichheit, mißachtet, und somit gilt offenbar als gerecht, wer Gesetz
und wer bürgerliche Gleichheit achtet. Das Gerechte ist folglich die Achtung von
Gesetz und bürgerlicher Gleichheit, das Ungerechte die Mißachtung von Gesetz und
bürgerlicher Gleichheit. (Aus der Nikomachischen Ethik)
Anmerkungen zur Implikation und Bi-implikation Die Implikation ist der „umstrittendste“ Junktor, da man bei ihm üblicherweise die größten Schwierigkeiten hat, den Bezug
zur Folgerungsbeziehung, wie wir sie im Alltag gebrauchen, zu sehen. Bei dieser erwartet man
einen inhaltlichen, vielleicht sogar einen kausalen Bezug zwischen dem, was folgt, und dem,
woraus es folgt. Im Alltag gelten die sogenannten Paradoxa der Implikation, also die Regeln
ex falso quodlibet und verum ex quodlibet nicht. Daher verwendet manche Autoren gerne andere Bezeichnungen wie Subjunktion oder Konditional statt Implikation, oder die Implikation
wird als materiale Implikation spezifiziert, um sie von dem intuitiven Implikationsbegriff zu
unterscheiden.
Die einfachste Art des Umgangs ist sicher, die Wahrheitstafel als Definition für etwas, was mit
→ bezeichnet wird, zu akzeptieren, ohne sich weitere Gedanken darüber zu machen, was dies
nun genau ist. Man kann sich allerdings überlegen, daß diese Definition auch sinnvoll ist.
6 Mitgeteilt
von Frieder Vogelmann.
30
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
Der pragmatische Standpunkt stellt dazu fest, daß keine andere Wahrheitswertverteilung besser
als Implikation geeignet wäre. Die beiden Alternativen, an die man vielleicht denken könnte,
haben bereits andere Namen – Bi-implikation und Konjunktion – und geben klare logische
Konzepte wieder, die sich deutlich von der erwünschten Implikation unterscheiden.
Einer inhaltlichen Verteidigung kann man die Vorstellung zugrundelegen, daß die Zuordnung
von Wahrheitswerten einem Informationsgehalt entspricht: W bedeutet, daß man einen Satz als
richtig akzeptiert, F, daß man ihn verwirft. Eine Konjunktion akzeptiert man dann und nur
dann, wenn man beide Teilinformationen akzeptiert; eine Disjunktion, wenn man mindestens
eine der beiden akzeptiert. In diesem Sinne steht die Implikation (A → B) dafür, daß unter der
Annahme, daß A gilt, auch B akzeptiert werden soll. Man kann es auch als eine Art (Rechen–)
Prozeß oder als ein Computerprogramm verstehen, das unter der Eingabe A das Ergebnis B
(A → B) gelten soll: Wenn eine akzeptierte Eingabe
liefert. Unstrittig ist nun, daß A B
W F
F
eine verworfene Ausgabe produziert, ist der Prozeß fehlerhaft. Dahingegen wird ein fehlerfreier
Prozeß bei fehlerhafter Eingabe in der Regel ein fehlerhaftes Ergebnis produzieren, muß es aber
nicht, denn den Prozeß kann man sich immer auch als eine Art Informationsverlust vorstellen
(B enthält weniger Information als A), wo gerade das Fehlerhafte verschwunden ist. Umgekehrt
kann ein fehlerhafter Prozeß sowohl aus richtigen als auch aus falschen Eingaben sowohl falsche
als auch (zufällig) richtige Ausgaben liefern.
Es gäbe nun die skeptische Version, bei der man die drei verbleibenden Spalten alle mit F auffüllt, da ja stets ein Fehler passiert sein kann. Dann hätte man eine Implikation, die immer
dann W liefert, wenn mit Sicherheit kein Fehler aufgetreten ist, und stets ein F, wenn ein Fehler
passiert ist und ein Zweifel vorliegt. Aber da diese Wahrheitsverteilung stets F liefert, hat sie
gar keine Aussagekraft.
Im Gegensatz dazu gibt es die „positive“ Variante in dubio pro reo, welche die verbleibenden
Spalten alle mit W auffüllt, da ja stets etwas Richtiges geschehen sein kann. Diese Implikation
(nämlich die unsre) liefert ein F, wenn mit Sicherheit ein Fehler aufgetreten ist, und W, wenn
etwa Richtiges geschehen ist oder ein Zweifel vorliegt. Darauf ist die Aussagenlogik aufgebaut,
was bedeutet: Wenn die Aussagenlogik einen Fehler erkennt, dann liegt auch wirklich einer vor,
aber sie erkennt nicht alle. Daraus ergibt sich im Gegenzug aber, daß eine Formel aber auch nur
dann eine Tautologie sein kann, wenn ein Grund in der aussagenlogischen Struktur der Formel
vorliegt.
Mischvarianten, die manche Spalten mit F und andere mit W auffüllen würden (etwas nach
„Fehlerwahrscheinlichkeit“ – dann würde man vermutlich die Wahrheitswertverteilung der Biimplikation bekommen), hätten ebenfalls den Nachteil, keine verläßliche Aussage mehr zu liefern.
Eine Implikation (A → B) kann man durch „wenn A, dann B“ wiedergeben, oder, in umgekehrter Reihenfolge, mit „B folgt aus A“ oder „B, falls A“, oder durch Ähnliches.
Zu beachten ist, daß es neben dem verbreiteten Fehlschluß, aus (A → B) die anders gerichtete
Implikation (B → A) zu folgern, auch das umgekehrte Phänomen gibt: daß nur eine Implikation gesagt wird, aber eine Bi-implikation gemeint ist. Wenn die Eltern ihrem Kind sagen:
„Wenn Du Deine Hausaufgaben machst, darfst Du fernsehen“, hört das Kind wahrscheinlich
eher „Wenn Du Deine Hausaufgaben nicht machst, darfst Du nicht fernsehen“, und das war
wohl ebenfalls gemeint, d.h. die sprachliche Implikation gibt hier eine logische Bi-implikation
wieder. Im Einzelfall ist es oft schwierig zu entscheiden, ob hinter einer sprachlichen Implikation
eine Bi-implikation steht.
Hinter einer Wendung wie „A nur dann, wenn B“ steckt eine umgekehrte Implikation (A → B).
Die Bi-implikation hat keine schöne sprachliche Übersetzung: sind äquivalent oder sind gleichwertig; etwas mathematischer dann und nur dann, wenn oder genau dann wenn. Wie schon oben
bei der Implikation erwähnt, versteckt sich eine Bi-implikation oft hinter einer sprachlichen Implikation. Etwa im Beispiel „Bei der NATO bestimmen die Mitgliedsdstaaten. Ein Beschluß wird
nur gefaßt, wenn alle zustimmen können.“, denn man kann annehmen, daß, wenn alle zustimmen
können, auch ein Beschluß gefaßt wird. Bei Kant findet sich die Wendung nur alsdann, wenn,
31
M. Junker „Formale Logik“
Version vom 10. Dezember 2012
die wohl zumindest im folgenden Beispiel eine Bi-implikation darstellt: „Ein Geschmacksurteil
würde in Ansehung eines Gegenstandes von bestimmtem inneren Zwecke nur alsdann rein sein,
wenn der Urteilende entweder von diesem Zwecke keinen Begriff hätte, oder in seinem Urteile
davon abstrahierte.“
Anmerkungen zu mehrstelligen Junktoren An mehrstelligen Junktoren tauchen in der
natürlichen Sprache iterierte Konstruktionen wie etwa ... und ... und ..., (entweder) ... oder
... oder .... Diese könnte man auch als mehrfache Anwendung der betreffenden zweistelligen
Junktors auffassen (was bis auf logische Äquivalenz keinen Unterschied ergibt); da aber alle
Glieder gleichberechtigt auftreten und in der Regel keine Klammerung erkennbar ist, sind sie
vom Charakter her doch eher höherstellig. Bei weder ... noch ... noch geht dies nicht, da ∨|
nicht kommutativ ist: „Weder A, noch B, noch C“ wird korrekt mit (¬A ∧ ¬B ∧ ¬C) übersetzt,
was weder logisch äquivalent zu ((A ∨| B) ∨| C) noch zu (A ∨| (B ∨| C)) ist.
Ein weiteres Beispiel eines dreistelligen sprachlichen Junktors ist falls ... dann ... sonst ....
Beispiele für echte höherstellige Junktoren scheinen selten. Häufig sind dagegen zusammengesetzte Formulierungen, bei denen die Klammerung nicht vollkommen klar ist. Bedeutet „Aus A
oder B folgt C“ nun ((A ∨ B) → C) oder ((A → C) ∨ (B → C))? Wofür steht im Einzelfall
„Nicht A oder B“: für ¬(A ∨ B) oder für (¬A ∨ B) oder gar für (¬A ∨ ¬B)?
Eine ausführliche Darstellung von Übersetzungsfragen findet sich in:
• Ansgar Beckermann Einführung in die Logik, 2. Auflage, Berlin: de Gruyter 2003.
32