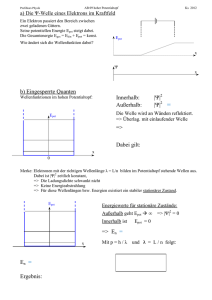
1 Arbeit und Energie

1
Arbeit und Energie
~ auf einen
Von Arbeit sprechen wir, wenn eine Kraft F
Körper entlang eines Weges ~s einwirkt und dadurch der
"Energieinhalt" des Körpers verändert wird. Die Arbeit
ist de…niert als das Skalarprodukt von Kraft und Weg
~ ~s =
W1!2 = F
ZP2
~ d~
F
r:
(1)
P1
Beispiel für die Berechnung eines Wegintegrals:
Eine Kraft die senkrecht zur Bahn des Körpers wirkt,
vermag den Betrag der Geschwindigkeit des Körpers nicht
zu verändern und leistet deshalb keine Arbeit an dem
Körper. Arbeit und Energie werden in gleichen Einheiten
gemessen, im SI System ist dies das Joule
kg m2
1 J = 1 Nm = 1 2
s
(2)
2
Konservative Kraftfelder
~ nur von der
Hängt die Arbeit gemäß(1) im Kraftfeld F
Lage der Punkte P1 und P2 ab, nicht aber von dem Weg
der zwischen diesen Punkten zurückgelegt wird, so verschwindet auf jedem geschlossenen Weg die resultierende
Arbeit
I
~ d~
F
r = 0;
(3)
. Ein solches Kraftfeld heiß
t konservativ. Die Bedeutung
konservativer Kraftfelder liegt darin, dass sie die mechanische Energie eines Körpers, der sich darin bewegt erhalten, d.h. die Summe von potentieller und kinetischer
Energie ist konstant
1
Ekin + Epot = m 2 + Epot = konstant.
2
(4)
Wichtige konservative Kräfte: alle Zentralkräfte wie beispielsweise Gravitationskraft, Coulombkraft, Federkraft sowie
alle elastischen Kräfte
~ (~
Beispiel: konstantes Kraftfeld F
r) = m~g
~ (x; y ) = py ~ex
Gegenbeispiel: F
Notwendige Bedingungen für konservative Kräfte:
Die Kraft darf nur eine Funktion des Ortes sein
Sie muss am gleichen Ort zeitlich konstant sein.
Sie darf nicht vom Bewegungszustand des Körpers,
etwa seiner Geschwindigkeit, abhängen. Diese Forderung schließ
t insbesondere Reibungskräfte aus.
Dies sind notwendige, aber keine hinreichenden Bedingungen für ein konservatives Kraftfeld.
~ (~
Gegenbeispiel: F
r) = (y;
x),
Für nichtkonservative Kräfte (z.B. die Reibungskraft, sowie
alle zeitabhängigen Kräfte) ist die Summe der mechanischen Energie nicht unbedingt konstant. Die Gesamtenergie einschließ
lich der thermischen, elektrischen, atomaren, nuklearen, etc. Energien, bleibt in einem abgeschlossenen System immer konstant. Dies ist eine grundlegende
Erfahrungstatsache.
3
Das Potential
~ kann man einen RefIn einem konservativen Kraftfeld F
erenzpunkt P0 wählen und jeden anderen Punkt P1 durch
die Arbeit charakterisieren, die man aufbringen muss, um
~ , von P0 dorthin zu bringen
ihn gegen die Kraft F
Epot(P1) =
ZP1
P0
~ d~
F
r:
(5)
Mit Epot(~
r) ordnet man jedem Punkt im Raum eine
skalare Größ
e, das Potential, zu (lat.: potentialis, von
potentia Macht, Kraft, Leistung). Es handelt sich also
um ein Skalarfeld, d.h. einer skalaren Funktion des Ortes.
Die Wahl des Refernzpunktes P0 ist dabei ebenso willkürlich wie die Festlegung des dortigen Potentials. Von Bedeutung ist lediglich die Di¤erenz der so de…nierten potentiellen Energie zwischen einem Anfangspunkt P1 und
einem Endpunkt P2
Epot(P1)
ZP1
Epot(P2) =
P0
=
ZP2
~ d~
F
r+
ZP2
~ d~
F
r(6)
P0
~ d~
F
r = W1!2
(7)
P1
sie ist gleich der vom Kraftfeld geleisteten Arbeit.
Das Potential eines Kraftfeldes lässt sich leicht veranschaulichen, wenn man Punkte gleichen Potentials durch
eine Linie verbindet. Diese Linien werden als Äquipotentiallinien bezeichnet. Die Höhenlinien auf einer topographischen Karte sind die Äquipotentiallinien der potentiellen Energie im Schwerefeld der Erde.
In Umkehrung von (5) lässt sich jedes konservative Kraftfeld als Ableitung eines Potentials gewinnen: Im eindimensionalen Fall Epot = Epot(x), lautet dies
dEpot(x)
dx
während im dreidimensionalen Fall Epot = Epot(x; y; z )
die jeweilige Änderung von Epot in Richtung der verschiedenen Koordinatenachsen zu berücksichtigen ist
Fx =
0
~ (x; y; z ) =
F
=
=
@
Epot(x; y; z )
@x
@
Epot(x; y; z )
@y
@
Epot(x; y; z )
@z
grad Epot(x; y; z )
~ pot(x; y; z ):
rE
B
B
B
B
B
B
B
@
1
C
C
C
C
C
C
C
A
(8)
(9)
(10)
Der Klammerausdruck in (8) heisst Gradient der Funktion Epot und zeigt in die Richtung, in der Epot am stärksten wächst und sein Betrag ist proportional zur Steilheit mit der Epot wächst. Die Kraft hingegen besitzt
das negative Vorzeichen und ist deshalb immer entgegengesetzt, in Richtung der steilsten Abnahme von Epot,
gerichtet. Sie steht immer senkrecht auf den Äquipotentiallinien (im zweidimensionalen Fall), bzw. auf den
Äquipotential‡ächen (im dreidimensionalen Fall). Die
ist einleuchtend, da die Ableitung des Potentials entlang einer Äquipotentiallinie immer Null ist und daher
der Kraftvektor keine Komponente in dieser Richtung besitzen kann.
Beispiel:
Äquipotentiallinien und Kraft für Epot(x; y ) =
q
x2 + y 2