Polynome im Komplexen

4.4. Polynome über den komplexen Zahlen
4.4
87
Polynome über den komplexen Zahlen
Mithilfe der Polarkoordinaten können wir für jede Wahl einer natürlichen Zahl n die
Lösungen der Gleichung z n = 1, die sogenannten n-ten Einheitswurzeln angeben.
. Die Gleichung z n = 1 hat genau n
4.4.1 Satz Zu n ∈ N setzen wir ϕ := 2π
n
verschiedene Lösungen in C, nämlich die Zahlen
zk = eikϕ = cos(k
2π
2π
) + i sin(k ) für k = 0, 1, . . . , n − 1.
n
n
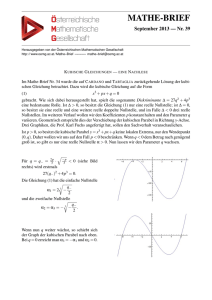
Diese Zahlen liegen auf dem Einheitskreis und bilden die Eckpunkte eines regelmässigen n-Ecks. Man beachte, dass das n-Eck spiegelsymmetrisch zur reellen Achse liegt.
Das bedeutet: Ist z eine n-te Einheitswurzel, so auch z.
Für n = 6 erhält man:
Im
z2
z1
ϕ
1
−1
z2 = z4
Re
z5 =z1
Beweis. Wir rechnen zuerst nach, dass die angegebenen Zahlen tatsächlich die Gleik2π
chung lösen: zkn = (ei n )n = eik2π = ei0 = 1. Nehmen wir jetzt umgekehrt an,
z = reiψ sei eine Lösung. Also ist z n = r n (eiψ )n = r n einψ = 1. Das bedeutet, r = 1
und nψ = k2π für ein k ∈ Z, oder ψ = k · 2π
= k · ϕ. Die Zahl z kommt also schon
n
in unserer Liste vor.
q.e.d.
2π
4.4.2 Beispiel Die
dritten Einheitswurzeln sind z0 = 1, z1 = ei 3 = − 12 + i
√
4π
z2 = ei 3 = − 12 − i 23 .
√
3
2
und
Folgerung: Die Gleichung z n = a (wobei a ∈ C\{0}) hat in C genau n verschiedene
√
ψ+k2π
Lösungen. Ist nämlich a = r · eiψ , so lauten die Lösungen zk = n r · ei n für
k = 0, 1, . . . , n − 1. Diese Zahlen sind wiederum die Eckpunkte eines regelmässigen
n-Ecks, das gegenüber dem n-Eck gebildet aus den n-ten Einheitswurzeln
um den
√
Winkel ψn um den Nullpunkt gedreht und mit dem Faktor n r multipliziert ist.
88
Kapitel 4. Komplexe Zahlen, Kreisfunktionen und Fourieranalyse
π
4.4.3 √
Beispiele
• Die Lösungen der Gleichung
z 3 = 8i lauten z0 = 2 · ei 6 =
√
2π
5π
π
3π
3 + i, z1 = 2 · ei( 6 + 3 ) = 2 · ei 6 = − 3 + i und z2 = 2 · ei 2 = −2i.
Im
z1
b
b
z0
ψ/3
Re
2
b
z3 = −2i
π
• Die Gleichung z 3 = −1
hat die Lösungen z0 = ei 3 = 21 +i
√
4π
π
z2 = ei 3 + 3 = 12 − i 23 = z0 .
√
3
,
2
π
2π
z1 = ei 3 + 3 = −1,
Schauen wir uns nun allgemeiner Gleichungen an der Form
an z n + an−1 z n−1 + . . . + a1 z + a0 = 0 ,
wobei die Zahlen aj ∈ C, an 6= 0 festgewählt sind. Der Ausdruck auf der linken Seite
der Gleichung ist also ein Polynom von Grad n in z. Ist an = 1, so spricht man von
einem normierten Polynom.
Die Nullstellen der Polynome von Grad 2 beschreibt die Mitternachtsformel,
und für die Fälle n = 3, 4 fanden italienische Mathematiker im 16. Jahrhundert
entsprechende Formeln.
Die Cardanosche Formel für die reelle Lösung der kubischen Gleichung
x3 + 3px + 2q = 0 (p, q ∈ R)
für den Fall D := q 2 + p3 > 0 lautet:
q
q
√
√
3
3
x1 = −q + D + −q − D .
In diesem Fall gibt es auch noch zwei zueinander konjugierte komplexe Lösungen,
nämlich
√ q
q
q
q
√
√
√
√
1 3
3 3
3
3
x2/3 = − ( −q + D + −q − D) ± i
( −q + D − −q − D) .
2
2
4.4.4 Beispiele
• Betrachten wir die Gleichung x3 + 6x + 2 = 0. Hier ist p = 2
3
und q = 1, und
D√
= q 2 + p√
= 9.√Die Formel von Cardano liefert die reelle
√
3
3
3
Lösung x1 = 2 + √
−4 = √ 2 − 3 4.√Ausserdem
√
√ gibt es noch die komplexen
Lösungen x2/3 = − 12 ( 3 2 − 3 −4) ± i 23 ( 3 2 − 3 −4).
4.4. Polynome über den komplexen Zahlen
89
• Wählen wir p = 0 und q = − 12 , kommen wir auf die Gleichung x3 − 1 = 0.
q
q
√
Hier ist D = 14 und daher x1 = 3 12 + 21 + 3 12 − 21 = 1 und x2/3 = − 12 ± i 23 ,
wir finden also wieder die bereits oben berechneten dritten Einheitswurzeln.
Ist die Diskriminante D = q 2 + p3 der kubischen Gleichung x3 + 3px + 2q = 0
negativ, tauchen in der Formel “unmögliche” Quadratwurzeln aus negativen Zahlen
√
auf, und das Zeichen 3 muss dann als mehrdeutige komplexe Wurzel interpretiert
werden. In diesem Fall kommt man sogar auf drei verschiedene reelle Nullstellen!
Wählen wir zum Beispiel q = 0 und p = −4. Dann ist q 2 + p3 = −64, und eine
komplexe Quadratwurzel daraus ist 8i. Die komplexen
dritten Wurzeln
der Zahl
√
√
w = 8i hatten wir oben bestimmt. Sie lauten z0 = 3 + i, z1 = − 3 + i, z2 = −2i.
Die dritten Wurzeln der Zahl √w = −8i bekommt
man durch Spiegelung an der
√
reellen Achse. Sie lauten z0 = 3 − i, z1 = − 3 − i, z2 = +2i. Addieren wir jetzt
gemäss der Cardanoschen Formel jeweils entsprechende dritte Wurzeln, erhalten wir
reelle Zahlen, denn xk := zk + zk = 2 Re(zk ) für k = 0, 1, 2.
Konkret liefert das für unseren Fall:
√
z0 + z0 = 2 3,
√
z1 + z1 = −2 3,
z2 + z2 = 0 .
Tatsächlich sind diese drei Zahlen die Lösungen der kubischen Gleichung
x3 − 12x = 0 .
Für Gleichungen von Grad n ≥ 5 gibt es keine entsprechenden allgemeinen
Lösungsformeln. Aber man kann beweisen, dass jede solche Gleichung über den
komplexen Zahlen Lösungen hat.
Fundamentalsatz der Algebra: Über C hat jedes Polynom von Grad n ∈ N
eine Nullstelle.
Per Induktion folgt durch Polynomdivision aus diesem Satz sogar, dass jede
Gleichung von Grad n genau n Lösungen hat, wenn man die Vielfachheiten mitzählt.
Genauer gilt folgendes:
4.4.5 Satz Sei p(z) = z n + an−1 z n−1 + . . . + a1 z + a0 ein Polynom von Grad n ∈ N
mit Koeffizienten aj ∈ C. Dann gibt es komplexe Zahlen z1 , . . . , zn ∈ C mit
z n + an−1 z n−1 + . . . + a1 z + a0 = (z − z1 )(z − z2 ) . . . (z − zn ) .
Die Liste der zj besteht aus sämtlichen Nullstellen des Polynoms p, dabei können
Nullstellen auch mehrfach aufgelistet sein. Die Häufigkeit, mit der eine bestimmte
Nullstelle in der Liste vorkommt, bezeichnet man als Vielfachheit der Nullstelle.
Der Beweis des Fundamentalsatzes der Algebra ist schwierig und kann an dieser
Stelle nicht gegeben werden, weil man dafür mehr Theorie benötigt.
90
Kapitel 4. Komplexe Zahlen, Kreisfunktionen und Fourieranalyse
4.4.6 Beispiele
1. Das Polynom p(z) = z 2 +a (a ∈ R, a > 0) hat die
√ Nullstellen
√
√
±i a, und wir können es als Produkt in der Form p(z) = (z − i a)(z + i a)
schreiben.
2. Das Polynom p(z) = z 3 − 1 hat als Nullstellen
in C gerade die√dritten Ein√
2π
1
3
3
heitswurzeln z0 = 1, z1 = e = − 2 + i 2 und z2 = z1 = − 21 − i 23 und
√
√
1
3
3
1
3
2
p(z) = z − 1 = (z − 1)(z + z + 1) = (z − 1)(z + ( + i
))(z + ( − i
)) .
2
2
2
2
3. Das Polynom p(z) = z 3 − 4z + 3 hat offenbar die Nullstelle z1 = 1. Es gilt:
p(z) : (z − 1) = (z 3 − 4z + 3) : (z √
− 1) = z 2 + z − 3. Die Nullstellen dieses
quadratischen Polynoms lauten −1±2 13 . Also hat p die Zerlegung:
√
√
1 + 13
1 − 13
3
2
)(z +
).
p(z) = z − 4z + 3 = (z − 1)(z + z − 3) = (z − 1)(z +
2
2
√
4. Das Polynom p(z) = z 4 + 3z 2 + 2 hat die Nullstellen ±i und ±i 2, es lässt
sich also folgendermassen zerlegen:
√
√
p(z) = (z 2 + 1)(z 2 + 2) = (z − i)(z + i)(z − i 2)(z + i 2) .
5. In den bisherigen Beispielen gab es nur einfache Nullstellen. Hier ein Polynom
mit einer doppelten und einer dreifachen Nullstelle:
p(z) = (z 2 − 4z + 4)(z 3 + 3z 2 + 3z + 1) = (z − 2)2 (z + 1)3 .
4.4.7 Bemerkung Sind alle Koeffizienten des Polynoms p reell, und ist w eine
Nullstelle, so ist auch w eine Nullstelle und zwar von derselben Vielfachheit. In
diesem Fall lässt sich p (über R) durch das quadratische reelle Polynom q(x) =
x2 − (2 Re(w))x + |w|2 teilen.
Beweis. Sind alle Koeffizienten ak des Polynoms p reell, so folgt mit den Rechenregeln für die komplexe Konjugation aus p(w) = 0:
0 = p(w) = w n + an−1 w n−1 + . . . + a1 w + a0 = wn +an−1 w n−1 +. . .+a1 w+a0 = p(w) .
Das bedeutet: Ist w eine Nullstelle von p, so auch w. Ist ausserdem w 6= w, so können
wir p durch das quadratische Polynom q := (z−w)(z−w) = z 2 −(w+w)z+w·w teilen.
Da w + w = 2 Re(w) und w · w = |w|2 reelle Zahlen sind, ist q ein reelles Polynom.
Nach Teilung von p durch q bleibt also ein reelles Polynom kleineren Grades übrig.
Per Induktion über den Grad kann man nun schliessen, dass die Vielfachheiten der
Nullstelle w und der Nullstelle w miteinander übereinstimmen.
q.e.d.
4.4.8 Folgerung Reelle Polynome von Grad n > 0 lassen sich über R vollständig
in ein Produkt aus Polynomen von Grad ≤ 2 zerlegen.