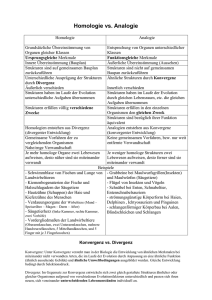
Martingale und Brownsche Bewegung

Martingale und Brownsche Bewegung
Martin G. Riedler
Institute for Stochastics, Johannes Kepler University
4040 Linz, Austria
[email protected]
2
Die vorliegenden Unterlagen sind ein Skriptum zur Vorlesung Martingale und Brownsche
Bewegung abgehalten im Sommersemester 2012 an der Johannes Kepler Universität Linz
im Umfang von zwei Semesterwochenstunden. Die Vorlesung präsentiert die Grundlagen
um einen allgemeinen Integrationsbegriff bezüglich von Martingalen darauf aufbauend einzuführen, behandelt aber den stochastischen Integrationsbegriff selbst nicht. Der Inhalt der
Vorlesung ist zum grössten Teil aus den unten angegebenen Monographien übernommen
mit der einen Ausnahme des Kapitels zu Reihenentwicklungen der Brownschen Bewegung.
Martin Riedler, Linz am 23. Juli 2012
Literaturverzeichnis
[EK86] S. N. Ethier and T. G. Kurtz. Markov Processes: Characterization and Convergence. Wiley, New York, 1986.
[JS87] J. Jacod and A. N. Shiryaev. Limit Theorems for Stochastic Processes. Springer,
Berlin, 1987.
[KS91] I. Karatzas and S. E. Shreve. Brownian Motion and Stochastic Calculus, 2nd Ed.
Springer, New York, 1991.
[Mét82] M. Métivier. Semimartingales. deGruyter, Berlin, 1982.
[Pro04] P. E. Protter. Stochastic Integration and Differential Equations, 2nd Ed. Springer,
Berlin, 2004.
[RY99] D. Revuz and M. Yor. Brownian Motion and Stochastic Calculus, 3rd Ed. Springer,
Berlin, 1999.
3
4
Inhaltsverzeichnis
1 Stochastische Prozesse
2 Die
2.1
2.2
2.3
2.4
7
Brownsche Bewegung
Existenz der Brownschen Bewegung . . . . . . . . . .
Pfadeigenschaften der Brownschen Bewegung . . . . .
Verwandte Prozesse . . . . . . . . . . . . . . . . . . .
Reihenentwicklung der Brownschen Bewegung . . . .
2.4.1 Satz von Levy-Ciesielski und die Paley-Wiener
2.4.2 Karhunen-Loève Entwicklung . . . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
Entwicklung
. . . . . . . .
3 Martingale
3.1 Martingalungleichungen . . . . . . . . . . . . . . . . . . . . . .
3.2 Regularitätsatz für Submartingale . . . . . . . . . . . . . . . . .
3.3 Martingalkonvergenzsätze . . . . . . . . . . . . . . . . . . . . .
3.4 Optional Stopping Theorem . . . . . . . . . . . . . . . . . . . .
3.5 Die Doob-Meyer Zerlegung & die quadratische Variation . . . .
3.5.1 Erweiterungen des Konzepts der quadratischen Variation
3.6 Schwache Konvergenz von Martingalen . . . . . . . . . . . . . .
A Gleichgradige Integrierbarkeit
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
17
17
20
24
28
28
32
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
39
42
46
47
51
55
63
65
71
5
6
INHALTSVERZEICHNIS
Kapitel 1
Stochastische Prozesse
Wir behandeln kurz die grundlegenden Definitionen bezügich der Theorie stochastischer Prozesse in stetiger Zeit. Das Kapitel ist eine Zusammenfassung und
ersetzt nicht eine detaillierte Einfhrung. Das Hauptziel ist die Terminologie und
Notation für die späteren Überlegungen zu fixieren.
Im folgenden sei (Ω, F, P) stets ein Wahrscheinlichkeitsraum, dieser heißt vollständig, falls
die σ-Algebra F jede Teilmenge aller P-Nullmengen enthält, d.h., B ∈ F mit P(B) = 0
und A ⊂ B impliziert A ∈ F. Eine Eigenschaft von Abbildungen auf einem Wahrscheinlichkeitsraum gilt fast sicher (f.s.) falls eine messbare Menge Ω0 ⊂ Ω existiert sodass diese
Eigenschaft für alle ω ∈ Ω gilt und P(Ωc0 ) = 0, d.h., die Eigenschaft gilt bis auf höchstens
einer Nullmenge.
Ein stochastischer Prozess X = (Xt )t∈I ist eine Familie von Zufallsvariablen1 Xt : Ω → E
definiert auf dem Wahrscheinlichkeitsraum (Ω, F, P) mit Werten in einem messbaren Raum
(E, E), genannt Zustandsraum, und Indexmenge I. Ein stochastischer Prozess heißt diskret
oder zeit-diskret wenn I ⊆ R+ höchstens abzählbar ist, z. B., I = N, und kontinuierlich
oder zeit-stetig falls I ⊆ R+ überabzählbar ist, z. B., I = [0, T ] ⊂ R+ oder I = R+ .
Ein Prozess heißt reell falls sein Zustandsraum die reellen Zahlen ausgestattet mit der
Borel-σ-Algebra ist, in Zeichen (E, E) = (R, BR ). Wir werden nachfolgend ausschließlich
kontinuierliche, meist reelle Prozesse behandeln. Im Folgenden bezeichnet daher die Indexmenge I immer eine überabzählbare Menge.
Sei p ≥ 1, dann heißt ein stochastischer Prozess X p-fach integrierbar, falls E|Xt |p < ∞
für alle t ∈ I. Im Falle p = 1 oder p = 2 heißt der Prozess integrierbar bzw. quadratintegrierbar.
Ein Prozess X besitzt unabhängige Inkremente (Zuwächse) falls für alle t1 ≤ t2 ≤ t3 ≤
t4 die Inkremente Xt2 − Xt1 und Xt4 − Xt3 unabhängig sind und er besitzt stationäre
Inkremente falls für alle t, h ≥ 0 die Verteilung der Inkremente Xt+h − Xt nur von h
1
Wir verwenden den Begriff Zufallsvariable wie in der Stochastik üblich als Synonym für messbare
Abbildung.
7
8
KAPITEL 1. STOCHASTISCHE PROZESSE
abhängt und unabängig von t ist.2
Ein Prozess X heißt stationär falls (Xt1 , . . . , Xtn ) und (Xt1 +h , . . . , Xtn +h ) für alle h ≥ 0
dieselbe Verteilung besitzen für alle endlich-vielen Indices t1 , . . . , tn ∈ I.
Neben der Interpretation eines stochastischen Prozesses als eine Familie von Zufallsvariable sind auch noch folgende Interpretationen möglich und theoretisch wichtig. Einerseits
können wir X als eine Abbildung der beiden Argument (t, ω) betrachten, d.h., als Abbildung X : I × Ω → E auffassen und andererseits, können wir die Familie (Xt )t∈I als eine
Zufallsvariable mit Werten in E I ausgestattet mit der Produkt-σ-Algebra E I betrachten,
d.h., als messbare Abbildung X : Ω → E I in die Menge der Pfade.
Pfadeigenschaften stochastischer Prozesse:
Sei X ein stochastischer Prozess, dann heißt für jedes fixe ω ∈ Ω die Abbildung t 7→ Xt (ω)
eine Trajektorie oder ein Pfad des Prozesses. Ein Prozess heißt (f.s.) (rechts-/links-)stetig
falls (fast alle) Trajektorien (rechts-/links-)stetig sind. Ein Prozess heißt càdlàg falls er
überall (!), d.h., für alle ω ∈ Ω, rechts-stetig ist und seine linken Limiten existieren.3 Ein
Prozess X ist (f.s.) lokal Hölderstetig mit Exponent γ > 0, falls für jedes T > 0 eine (f.s.)
positive Zufallsvariable h existiert und eine Konstante L < ∞, sodass
|Xt (ω) − Xs (ω)|
≤ L für (fast) alle ω ∈ Ω .
|t − s|γ
0<|t−s|<h(ω),
sup
t,s∈[0,T ]
Dies ist äquivalent zu der Bedingung, dass für (fast) alle ω ∈ Ω gilt
|Xt (ω) − Xs (ω)| ≤ L |t − s|γ
∀ t, s ∈ [0, T ] mit |t − s| < h(ω) .
Umgekehrt gilt, ein Prozess ist (f.s.) nirgends lokal Hölderstetig mit Exponent γ, falls kein
T > 0 existiert, sodass obige Bedingung (f.s.) erfüllt ist. (Lokale) Hölderstetigkeit mit
Exponent γ = 1 ist (lokale) Lipschitzstetigkeit.
Die nachfolgenden Grössen, die sich aus den Pfaden bestimmen, beschreiben deren Oszillationsverhalten. Eine Partition oder Zerlegung P[a,b] eines Intervalls [a, b] ist eine Menge
von Punkten t0 , . . . , tn ∈ [a, b] mit a = t0 ≤ t1 . . . ≤ tn = b und |P[a,b] | = maxi |ti − ti−1 | ist
die Feinheit der Partition, wobei hier und immer in Verbindung mit Partitionen der Index
i einmal die Anzahl der Elemente (ohne t0 ) durchläuft. Im folgenden sei X ein zeit-stetiger
stochastischer Prozess, dann heißt für [a, b] ∈ I die Größe
X
p
V[a,b]
(X) = sup
|Xti − Xti−1 |p
P[a,b]
2
i
Diese Bedingung heißt oft auch stark stationär im Gegensatz zu schwach stationär welche nur die
Gleichheit der der ersten beiden Momente fordert.
3
Das Gegenteil ist càglàd falls der Prozess linksstetig mit existierenden rechten Limiten ist.
9
die totale p-Variation über [a, b] des Prozesses. Das Supremum wird hier über alle Partitionen des Intervalls [a, b] genommen. Die totale Variation entspricht pfadweise dem ‘klassip
schen’ Variationskonzept der Analysis. Falls V[a,b]
(X) < ∞ (f.s.) für alle endlichen Intervalle
[a, b] ⊂ I dann ist der Prozess von (f.s.) endlicher totaler p-Variation. Falls p = 1, dann
sprechen wir einfach von der totalen Variation. Ein zweites, ‘stochastisches’ Variationskonzept ist das folgende. Wir bezeichnen die stochastische Grösse
X
|Xti − Xti−1 |p ,
Lp[a,b] := p-lim |P[a,b] |→0
i
falls dieser Grenzwert4 existiert, als p-Variation über [a, b], wobei der Grenzwert als Limes in
Wahrscheinlichkeit für beliebige Folgen von Partitionen deren Feinheit gegen 0 konvergiert
zu interpretieren ist und unabhängig von der Wahl der Folge zu sein hat. Falls p = 2
sprechen wir von der quadratischen Variation.
Äquivalenzbegriffe zwischen Stochastischen Prozessen
Der einfachste aber zu restriktive Begriff der Äquivalenz ist falls zwei Prozesse X, Y dieselbe Abbildung auf I × Ω definieren, d.h., Xt (ω) = Yt (ω) für alle (ω, t) ∈ Ω × I. Diese
Äquivalenzauffasung kann unter Beiziehung eines Wahrscheinlichkeitsmasses P in dreifacher Weise zu passenderen Konzepten abgeschwächt werden.5 Zwei Prozesse X und Y
mit Werten in E definiert auf den Wahrscheinlichkeitsräumen (Ω, F, P) und (Ω0 , F 0 , P0 ),
sind Versionen voneinander falls sie dieselben endlich-dimensionalen Verteilungen besitzen,
d.h.,
P Xt1 ∈ A1 , . . . , Xtn ∈ An = P0 Yt1 ∈ A1 , . . . , Ytn ∈ An
für alle messbaren Mengen Ai ⊂ E und alle endlichen Mengen von Indices {t1 , . . . , tn } ⊂
I. Falls die Prozesse X, Y auf dem selben Wahrscheinlichkeitsraum definiert sind und
für alle t ∈ I gilt, dass P[Xt = Yt ] = 1, dann heißen sie Modifikationen voneinander.
Schlussendlich die beiden Prozesse sind ununterscheidbar falls P[Xt = Yt ∀ t ∈ I] = 1, d.h.,
Trajektorien unterscheiden sich nur auf einer Nullmenge. Im falle diskreter Prozesse sind
die Begriffe Modifikation und ununterscheidbar äquivalent. Im Allgemeinen gelten zwischen
den Äquivalenzbegriffen die Beziehungen
X, Y ununterscheidbar =⇒ X, Y Modifikationen =⇒ X, Y Versionen
4
Wir verwenden die Notation p-lim und qm-lim um Konvergenz in Wahrscheinlichkeit und Konvergenz
im Quadratmittel zu bezeichnen, d.h.,
p-limn→∞ Xn = X
↔
∀ > 0 : limn→∞ P[|Xn − X| > ] = 0,
bzw.,
qm-limn→∞ Xn = X
5
↔
limn→∞ E|Xn − X|2 = 0
Alle drei sind Äquivalenzrelationen auf einer passenden Menge von Prozessen.
10
KAPITEL 1. STOCHASTISCHE PROZESSE
und umgekehrt
X, Y Modifikationen, X, Y f.s. rechts- oder linksstetig =⇒ X, Y ununterscheidbar .
Aus diesen Eigenschaften folgt, dass die Äquivalenzklasse der Modifikationen eines Prozesses (bis auf Ununterscheidbarkeit) höchstens einen f.s. (rechts-/links-)stetigen Prozess
enthält. Daher sagen wir f.s. (rechts-/links-)stetige Prozesse sind bis auf Unuterscheidbarkeit eindeutig definiert. Pfadeigenschaften bleiben nicht unter Modifikationen erhalten.
Oft sucht man jene Modifikation, die gute Pfadeigenschaften hat. Durch Abänderung eines
Prozesses auf der Nullmenge zu (rechts-/links-)stetigen Pfaden können wir immer einen
(rechts-/links-)stetige ununterscheidbaren Prozessen erhalten.
Die beiden schwächeren Äquivalenzbegriffe sind für die Anwendungen überaus wichtig, da
sehr oft durch physikalische Überlegungen und Experimente nur Aussagen über die endlich
dimensionale Verteilungen getroffen werden können. Prozesse in diesen Äquivalenzklassen
können sehr unterschiedliche Pfadeigenschaften besitzen und daher kann man sich zur mathematischen Behandlung aus dieser Klasse jenen Prozess wählen, der bestmögliche Pfadeigenschaften besitzt. Abschließend sei noch einmal darauf hingewiesen, dass Versionen,
Modifikationen und Ununterscheidbarkeit bezüglich eines bestimmten Masses definiert sind
und diese Eigenschaften nicht erhalten bleiben müssen, wählt man eine anderes Mass.
Kanonische Wahrscheinlichkeitsräume
Wie bereits erwähnt gibt es auf Grund von Beobachtungen oft nur Aussagen über die endlich dimensionalen Verteilung Stochastischer Prozesse und es stellt sich – vor all bei kontinuierlichen Modellen – zuallererst die Frage der Existenz eines Stochastischen Prozesses,
der diese endlich-dimensionalen Verteilungen besitzt. Wir betrachten nun nur kontinuierliche Indexmengen I, da die folgenden Probleme bei diskreten Prozessen nicht auftreten.
Existiert ein Prozess, dann kann er als Zufallsvariable mit Werten im messbaren Raum
(E I , E I ) aufgefasst werden und seine Verteilung induziert ein Bildmass darauf. Um die
Existenz eines Prozesses zu zeigen, ist es nun ausreichend die Existenz dieses Masses auf
dem Raum (E I , E I ) zu zeigen. Dieser Raum aller möglichen Pfade nimmt den Platz des unspezifizierten Wahrscheinlichkeitsraumes (Ω, F, P) ein und heißt daher kanonischer Wahrscheinlichkeitsraum. Auf dem kanonische Raum ist ein stochastischer Prozess durch die
Familie der Koordinatenabbildungen ζt : E I → E : ω 7→ ζt (ω) := ω(t), t ∈ I definiert und
dieser heißt kanonischer Prozess. Die Produkt-σ-Algebra E I ist per definitionem die von
den Koordinatenabbildungen erzeugte σ-Algebra.
Eine Antwort auf die Existenzfrage liefert der folgende Satz von Kolmogorov. Zuvor bemerken wir das eine Familie endlich-dimensionaler Verteilungen (PJ )J⊂I, |J|<∞ projektiv ist,
falls für J = (t1 , . . . , tn ) und jede Permutation π von {1, . . . , n}
P(t1 ,...,tn ) A1 × . . . × An = P(tπ(1) ,...,tπ(n) ) Aπ(1) × . . . × Aπ(n)
und
P(t1 ,...,tn ) A1 × . . . × An−1 × E = P(t1 ,...,tn−1 ) A1 × . . . × An−1
11
gilt. Hier sind die endlich-dimensionale Verteilungen eine Familie von Wahrscheinlichkeitsmassen auf der Familie der Produkträume Eti × . . . Etn für alle endlich dimensionalen
Teilmengen {t1 , . . . , tn } ⊂ I. Es ist leicht zu überprüfen, dass die endlich-dimensionalen
Verteilungen eines Prozesses eine projektive Familie sind und der folgenden Satz ist in gewissem Sinne die Umkehrung dieser Aussage und liefert die Existenz eines stochastischen
Prozesses zu einer gegebenen Familie von endlich-dimensionalen Verteilungen.
Satz 1.1 (Kolmogorov-Existenz Satz). Sei (E, E) ein Polnischer Raum6 zusammen mit
seiner Borel-σ-Algebra. Dann existiert für jede Indexmenge I und jede projektive Familie von endlich-dimensionalen Verteilungen genau ein Wahrscheinlichkeitsmass P auf
(E I , E I ), dessen Randverteilungen mit den gegebenen endlich-dimensionalen Verteilungen
übereinstimmen, d.h., für beliebige endlich viele Indices ti und messbare Mengen Ai gilt
P ζt1 ∈ A1 , . . . , ζtn ∈ An = P(t1 ,...,tn ) A1 × . . . × An .
Ein schwerwiegender Nachteil dieser Konstruktion ist, dass die Produkt-σ-Algebra E I
nur Mengen enthält, die durch abzählbar viele Koordinaten festgelegt sind. Daher treten Messbarkeitsprobleme immer dann auf, wenn man Eigenschaften oder Funktionale des
Prozesses betrachtet, die von überabzählbar vielen einzelnen Zufallsvariablen abhängen.
Das prominenteste Beispiel unter diesen ist die Nicht-Messbarkeit der Menge
{ω ∈ E I : t 7→ ζt (ω) ist stetig}
im kanonischen Wahrscheinlichkeitsraum und analog, wenn nach, z.B., der Beschränktheit
oder Differenzierbarkeit der Pfade gefragt wird. Ähnliche Probleme treten auch auf, wenn
man für beliebige Prozess die Abbildungen
τ (ω) := inf{t > 0 : Xt (ω) > 0},
lims↓t Xs (ω),
sups≤t Xs (ω)
betrachtet. Hier kann man im Allgemeinen nicht davon ausgehen, dass diese Ausdrücke
wohldefiniert oder messbar sind. Diese letzteren Probleme können behoben werden, falls
man (f.s.) (rechts-/links-)stetige Prozesse betrachtet, da man nun Funktionale überabzählbar
vieler Zufallsvariablen oft auf Funktionale auf dichten, abzählbaren Mengen, z.B., Q,
zurückführen kann.
Es bleibt aber weiterhin das Problem zu zeigen, dass der Prozess derartige Pfade besitzt.
Auf Grund der Nicht-Messbarkeit der Menge der stetigen Pfade in (E I , E I ), kann man
nicht einfach vorgehen und zeigen, dass die Menge der unpassenden Pfade eine Nullmenge
ist. Um diese Schwierigkeit vorerst zu umgehen, schwächen wir den Begriff fast sicher
(nur für den Moment!) ab, und sagen ein kanonischer Prozess ist f. s. (rechts-/links-)stetig
falls jeder messbaren Menge in E I , die alle (rechts-/links-)stetigen Pfade enthält, Mass
1 zugewiesen wird.7 Ein einfaches, allgemeines Kriterium zur Überprüfung der Stetigkeit
liefert der folgende Satz.
6
Ein topologischer Raum heißt polnisch, falls er vollständig metrizierbar und separabel ist, vor allem
gilt, jeder polnische Raum ist ein Borelraum.
7
Zur genaueren Unterscheidung wird eine derartige Menge auch wesentlich für des Wahrscheinlichkeitsmass genannt werden.
12
KAPITEL 1. STOCHASTISCHE PROZESSE
Satz 1.2 (Kolmogorov-Centsov Stetigkeits Kriterium). Existieren für einen reellen Prozess
X drei Konstanten α, β, C > 0, sodass
E|Xt − Xs |α ≤ C|t − s|1+β
für alle t, s ≥ 0 gilt, dann besitzt X eine f.s. stetige Modifikation. Diese ist f.s. lokal
Hölder-stetig mit Exponent γ für alle γ ∈ (0, β/α).
Bemerkung 1.1. Man kann sogar zeigen, dass der Prozess eine überall stetige Modifikation
besitzt. Dazu ändert man die f.s. stetige Modifikation so ab, dass man alle nicht-stetigen
Pfade konstant gleich 0 setzt und dann lässt sich zeigen, dass dieser überall stetige Prozess
ebenfalls eine Modifikation ist.
Um f.s. (rechts-)stetige Prozesse besser behandeln zu können ist der kanonische Raum
(E I , E I ) meist nur ein Zwischenschritt und wird nachdem die Existenz eines Prozesses gesichert ist durch einen besser geeigneten Raum ersetzt. Im folgenden Bezeichnen wird mit
D(I, E) und C(I, E) die Menge der rechtsstetigen, bzw., stetigen Pfade von I nach E,
die klarerweise Teilmengen von E I sind. Ausgestattet mit der jeweiligen Spur-σ-Algebra
von E I werden beide zu messbaren Räumen. Die Spur-σ-Algebra entspricht auch der von
den Koordinatenabbildungen von D(I, E) bzw. C(I, E) nach E erzeugten σ-Algebra. Sind
die Pfade eines Prozesse f.s. (rechts-)stetig, dann erhält man durch die Einschränkung eines Masses auf E I auf diese Räume eindeutig(!) ein Wahrscheinlichkeitsmass, trotzdem
beide Mengen nicht messbare Teilmengen von E I sind. Die resultierenden Wahrscheinlichkeitsräume bestehen wiederum aus einer Menge von Funktionen und dazugehörigen
Koordinatenabbildungen und sind daher auch kanonische Räume.
Die kanonische Version eines Prozesses ist eine Version, die auf einem (passenden) kanonischen Raum definiert. Jeder Prozess besitzt eine eindeutige kanonische Version. Somit gilt
allgemein ein Prozess auf einem beliebigen Raum (Ω, F, P) ist f.s. (rechts-/links-)stetig (im
normalen Sinn) – wir können getrost annehmen, dass, z.B., {ω ∈ Ω : X(ω) ∈ C(R+ , E)} ∈
F – falls seine kanonische Version f.s. (rechts-/links-) stetig im neuen Sinne ist.
Filtrationen
Eine Familie von Teil-σ-Algebren Ft , t ∈ I, von F, heißt Filtration falls Fs ⊆ Ft für s ≤ t.
Diese heißt vollständig bezüglich P, falls der Wahrscheinlichkeitsraum (Ω, F, P) vollständig
ist und F0 alle P-Nullmengen in F enthält. Die Vollständigkeit der Filtration ist eine
Eigenschaft bezüglich eines bestimmten Masses und muss nicht erhalten bleiben wird ein
beliebiges anderes Mass gewählt.
Sei N P die Menge aller P-Nullmengen in F, dann ist die Augmentierung einer Filtration
jene Filtration bestehend aus den den σ-Algebren FtP := Ft ∨ N P . Ist F eine vollständige
σ-Algebra, dann ist die augmentierte Filtration eine vollständige Filtration und auch jede
σ-Algebra FtP ist vollständig. Daher ist es immer möglich auf einem vollständigen Wahrscheinlichkeitsraum aus einer beliebigen Filtration eine vollständige Filtration zu erhalten.
Die augmentierte Filtration ist im Allgemeinen größer als die Filtration, die man erhält,
13
wenn man jede σ-Algebra einzeln vervollständigt. Die Filtration, die man durch diese Prozedur erhält, heißt Vervollständigung. Sei NtP die Menge der P-Nullmengen in Ft dann
ist die Vervollständigung einer Filtration jene Filtration bestehend aus den σ-Algebren
P
P
F t := Ft ∨ NtP . Es gilt F t ⊆ FtP und diese Inklusion kann strikt sein. Caveat: Es gilt aber
das unter Umständen die Vervollständigung einer Filtration keine vollständige Filtration
liefert!
W
Zu gegebener Filtration
definieren
wir
die
σ-Algebren
F
:=
t−
s<t Fs für alle t ∈ I mit
T
W
F0− = F0 und F∞ = s∈I Fs und Ft+ := >0 Ft+ für alle t ∈ I. Eine Filtration (Ft )t∈I
heißt links-stetig falls Ft = Ft− für alle t ∈ I, rechts-stetig falls Ft = Ft+ für alle t ∈ I
und stetig falls sie sowohl links- als auch rechts-stetig ist. Die Filtrationen (Ft− )t∈I und
(Ft+ )t∈I sind links- bzw. recht-stetig per definitionem.
Ein Wahrscheinlichkeitsraum zusammen mit einer Filtration, in Zeichen, (Ω, F, (Ft )t∈I , P),
heißt filtrierter Wahrscheinlichkeitsraum. Dieser erfüllt die üblichen Bedingungen, falls die
Filtration vollständig und rechtsstetig ist.
Ein Prozess X heißt an die Filtration (Ft )t∈I adaptiert, falls für jedes t ∈ I die Zufallsvariable Xt messbar bezüglich Ft ist. Eine Modifikation eines adaptierten Prozesses ist nicht
notwendigerweise adaptiert. Ist aber die Filtration vollständig, dann ist jede Modifikation
eines adaptierten Prozesses ebenfalls adaptiert.
Eine spezielle Filtration ist die von einem Prozess erzeugte natürliche Filtration FtX :=
σ(Xs , s ≤ t), d.h., Ft ist die gröbste8 σ-Algebra, sodass alle Xs , s ≤ t, messbar bezüglich
dieser sind. Die natürliche Filtration ist die gröbste Filtration an die ein Prozess adaptiert
ist. Falls X ein endlich-dimensionaler reeller, links-stetiger Prozess ist, dann ist die erzeugte
Filtration (FtX )t≥0 links-stetig. Dies gilt aber nicht für Rechts-stetigkeit! Zum Beispiel, eine
Brownsche Bewegung ist stetig, aber die erzeugte Filtration ist nicht rechts-stetig.
Die augmentierte Filtration eines endlich-dimensionalen, reellen starken Markov Prozesses
ist rechts-stetig und ist der Prozess zusätzlich links-stetig dann ist die augmentierte Filtration stetig. Eine weitere wichtige Eigenschaft der augmentierten Filtration ist, das das
Augmentieren einer Filtration die starke Markoveigenschaft als auch die Martingaleigenschaft erhält. Somit können wir meist o.B.d.A. annehmen, dass ein derartiger Prozess auf
eine Wahrscheinlichkeitsraum definiert ist, der die üblichen Bedingungen erfüllt.
Bemerkung 1.2. Viele Eigenschaften von Prozessen, z.B., die Markov- oder Martingaleigenschaft, sind bezüglich einer gewissen Filtration oder σ-Algebra definiert. Wir werden im
Allgemeinen die Angabe der Filtration weglassen, falls keine Möglichkeit der Verwechslung
besteht. Falls doch, werden wir diese einfach als Prefix an das Attribut anhängen. So ist
zum Beispiel ein (Ft )t∈I -adaptierter Prozess ein Prozess X, der an die Filtration (Ft )t∈I
adaptiert ist.
Eigenschaften als Abbildung auf Ω × I:
Ein Prozess X ist messbar, falls die Abbildung X : I × Ω → E messbar bezüglich der
Produkt-σ-Algebra auf I × Ω ist. Der Satz von Fubini impliziert, dass Pfade messbarer
8
Sei F, F 0 zwei σ-Algebren, sodass F 0 ⊂ F, dann ist F 0 gröber als F, bzw., F ist feiner als F 0 .
14
KAPITEL 1. STOCHASTISCHE PROZESSE
Prozesse Borel-messbare Abbildungen auf I sind und ebenso t 7→ EXt , falls die Erwartung
definiert ist. Weiters gilt die Vertauschbarkeit der Integration, d.h., für I ⊂ I
Z
Z
Z
Z
E|Xt | dt < ∞ =⇒
Xt dt < ∞ f.s. und
EXt dt = E Xt dt .
I
I
I
I
Prozess mit rechts- oder links-stetigen Pfaden sind messbar. Die Einführung einer Filtration führt zum folgenden etwas stärkeren Konzept. Ein Prozess X heißt progressiv messbar
falls für alle t ∈ I die Zufallsvariablen Xs , s ≤ t, B[0,t] ⊗Ft -messbar sind. Progressivität impliziert Adaptivität und Messbarkeit. Umgekehrt gilt, adaptierte, rechts- oder links-stetige
Prozesse sind progressiv und ein messbarer, adaptierter Prozess besitzt eine progressiv
messbare Modifikation.
Weiters, die vorhersehbare σ-Algebra P ist die σ-Algebra auf Ω × I, die von allen linksstetigen, adaptierten Prozessen aufgefasst erzeugt wird. Es kann gezeigt werden, dass diese
mit der σ-Algebra die von allen stetigen Prozessen erzeugt wird übereinstimmt. Ein Pmessbarer Prozess heißt vorhersehbar.
Stoppzeiten
Eine Zufallsvariable τ mit Werten in R+ = R+ ∪ {∞} (zufällige Zeit) heißt Stoppzeit
bezüglich einer Filtration (Ft )t≥0 falls {τ ≤ t} ∈ Ft für alle t ∈ R+ .9 Die Stoppzeit heißt
(f.s.) endlich falls τ < ∞ (f.s.) und (f.s.) beschränkt falls τ ≤ T (f.s.) für ein T > 0. Jede
Stoppzeit kann von unten durch eine Folge beschränkter Stoppzeiten, z.B., τ ∧ n ↑ τ , und
von oben durch eine nicht-wachsende Folge von Stoppzeiten, die je nur abzählbare viele
Werte annehmen, z.B., τn ↓ τ falls

 i für i − 1 ≤ τ < i , i ∈ N,
n
2k
2n
2n
τ :=

∞ für τ = ∞ ,
approximiert werden. Sind τn , n ∈ N, Stoppzeiten und c ∈ [0, ∞), dann sind auch
τ1 + c,
τ1 ∧ c,
τ1 + τ2 ,
sup τn ,
n∈N
min τk , max τk ∀ n ∈ N
k≤n
k≤n
Stoppzeiten und, falls die Filtration rechtsstetig ist, sind auch
inf τn ,
n∈N
lim inf τn ,
n→∞
lim sup τn
n→∞
Stoppzeiten. Ein weitere wichtige Klasse zufälliger Zeiten sind Eintrittszeiten (‘hitting times’). Sei X eine adaptierter Prozess mit Werten in einem beliebigen metrischen Raum
und B eine Borelmenge, dann ist die zufällige Zeit
τB := inf{t ≥ 0 : Xt ∈ B} ,
9
Natürlich ist das Konzept analog für beliebige Indexmengen I definiert.
15
mit inf ∅ = ∞, eine Stoppzeit, falls entweder die Menge B offen und die Filtration rechtsstetig ist10 oder falls die Menge B abgeschlossen und zusätzlich entweder kompakt ist oder
der Prozess X linke Limiten besitzt. Erfüllt die Filtration die üblichen Bedingungen und
ist der Prozess progressiv messbar, dann ist jede Eintrittszeit eine Stoppzeit. Dieselben
Aussage gelten auch für Eintrittszeiten nach einer zufälligen Zeit, d.h. für zufällige Zeiten
τB,σ := inf{t ≥ σ : Xt ∈ B} wobei σ eine beliebige Zufallsvariable in R+ ist.
Sei τ eine Stoppzeit, dann ist die gestoppte σ-Algebra Fτ definiert durch
Fτ := A ∈ F : A ∩ {τ ≤ t} ∈ Ft für alle t ≥ 0 .
Klarerweise gilt Fτ ist eine σ-Algebra. Sind τ und σ zwei Stoppzeiten, dann sind τ und
τ ∧ σ Fτ -messbar und falls τ ≤ σ dann gilt Fτ ⊂ Fσ . Weiters, falls γ eine Fτ -messbare
Zufallsvariable ist, gilt nun, dass auch τ + γ eine Stoppzeit ist.
Sei X ein stochastischer Prozess und τ eine Stoppzeit. Dann definieren wir auf [τ < ∞]
die Abbildung Xτ : ω 7→ Xτ (ω) (ω). Existiert ein Zufallsvariable X∞ – o.B.d.A. kann man
z.B. immer X∞ konstant wählen –, dann kann diese Definition auf ganz Ω ausgedehnt
werden. Ist die Stoppzeit f.s. endlich und nimmt nur höchstens abzählbar viele Werte
an, dann ist Xτ eine Zufallsvariable falls der Prozess X adaptiert ist. Ist die Stoppzeit
f.s. beschränkt, aber nimmt überabzählbar viele Werte an, dann ist Xτ eine Zufallsvariable
falls der Prozess messbar ist. Ist der Prozess progressive messbar, dann ist Xτ für eine
beliebige Stoppzeit eine Zufallsvariable. Weiters, ist der Prozess X progressiv messbar,
dann ist die Zufallsvariable Xτ auch messbar bezüglich Fτ und der gestoppte Prozess X τ
definiert durch Xtτ := Xt∧τ , t ≥ 0, ist ebenfalls progressiv messbar.
10
Allgemeiner gilt, dass in diesem Falle τB eine (Ft+ )t≥0 -Stoppzeit ist.
16
KAPITEL 1. STOCHASTISCHE PROZESSE
Kapitel 2
Die Brownsche Bewegung
Wir definieren die Brownsche Bewegung und beweisen die Existenz und
Eindeutigkeit eines derartigen Prozesses. Wir analysieren die elementaren
(Pfad-)Eigenschaften der Brownschen Bewegung, diskutieren weitere stochastische Prozesse, die sich aus der Brownschen Bewegung gewinnen lassen. Zuletzt
präsentieren wir noch Reihendarstellungen der Brownschen Bewegung und beweisen die Karhunen-Loève-Entwicklung.
Ein stochastischer Prozess B = (Bt )t≥0 wird Brownsche Bewegung oder Wiener Prozess
genannt, falls er die folgenden Eigenschaften besitzt:
(a) Der Prozess startet fast sicher im Ursprung, d.h., B0 = 0 fast sicher,
(b) besitzt stationäre unabhängig normalverteilte Zuwächsen, d.h., Bt − Bs ∼ N (0, |t − s|)
und Bt2 − Bt1 unabhängig von Bt4 − Bt3 falls (t1 , t2 ) ∩ (t3 , t4 ) = ∅,
(c) und besitzt fast sicher stetige Pfade.
Bemerkung 2.1. Die hier gegebene Definition einer Brownschen Bewegung sowie die Resultate in diesem Kapitel kommen ohne die Angabe einer Filtration aus an welche die
Brownsche Bewegung adaptiert ist. Jedoch, in späteren Kapiteln wird eine solche benötigt
und in diesem Falle heißt ein Prozess B eine Brownschen Bewegung bezüglich der Filtration (Ft )t≥0 falls dieser (a)–(c) erfüllt, an die Filtration (Ft )t≥0 adaptiert ist und für alle
s < t gilt Bt − Bs ist unabhängig von Fs . Es ist offensichhtlich, dass diese zusätzlichen Bedingungen bereits die Unabhängigkeit der Inkremente implizieren. Andererseits gilt, dass
die Unabhängigkeit der Inkremente impliziert, dass eine Brownsche Bewegung immer eine
Brownsche Bewegung bezüglich ihrer natürlichen Filtration (FtB )t≥0 ist.
2.1
Existenz der Brownschen Bewegung
Im folgenden ersten Satz zur Brownschen Bewegung beweisen wir deren Existenz und Eindeutigkeit mittels des Satzes von Kolmogorov. Im weiteren Verlauf werden wir noch weitere
17
18
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
Möglichkeiten kennenlernen die Existenz und Eindeutigkeit zu beweisen. Klarerweise bezieht sich hier Eindeutigkeit auf die Verteilung der kanonischen Version.
Satz 2.1 (Existenz der Brownschen Bewegung). Es existiert genau ein stochastischer Prozess der die Bedingungen (a)–(c) erfüllt. Dieser heißt Brownsche Bewegung oder Wiener
Prozess.
Bemerkung 2.2. Aus dem Beweis folgt, dass die endlich-dimensionalen Verteilungen der
Brownschen Bewegung Normalverteilungen sind und für alle t, s ≥ 0 gilt Bt ∼ N (0, t) und
Cov(Bt , Bs ) = t ∧ s.
Beweis. Wir verwenden nun zum Beweis des Satzes den Kolmogorov Existenzsatz und das
Kolmogorov-Centsov Stetigkeitskriterium. Als Vorbemerkung zeigen wir, dass die endlichdimensionalen Verteilungen eines Prozesses der (a)–(c) erfüllt, multivariat normalverteilt
sind: Aus der Unabhängigkeit folgt für s < t, dass (Bs , Bt − Bs ) gemeinsam normalverteilt
sind und somit auch (1 0; 1 1)(Bs , Bt − Bs ) = (Bs , Bt ) mit Kovarianzmatrix (s s; s t) und
somit gilt Cov(Bs , Bt ) = s ∧ t. Analog folgt die gemeinsame Verteilung aller endlichen
Vektoren (Bt1 , . . . , Btn ).
Als nächstes konstruieren wir aus den Eigenschaften (a) und (b) eindeutig eine Familie endlich-dimensionaler Verteilungen – bestehend aus Normalverteilungen – und um die
Existenz und Eindeutigkeit eines Prozesses zu erhalten, ist zu zeigen, dass diese Familie
projektiv ist. Die Existenz einer regulären bedingten Erwartung garantiert, dass für t1 < t2
Z
P[Bt1 ∈ A1 , Bt2 ∈ A2 ] =
P[Bt2 ∈ A2 | Bt1 ] dPBt1
A1
wobei PBt1 die Verteilung von Bt1 bezeichnet. Aus der Unabhängigkeit der Inkremente folgt
nun
Z
(x − B )2 2
t1
dx2 ,
P Bt2 ∈ A2 Bt1 =
(2π(t2 − t1 ))−1/2 exp −
2(t
−
t
2
1)
A2
|
{z
}
=:p(t2 −t1 ,x2 −Bt1 )
da Bt1 + (Bt2 − Bt1 )|Bt1 ∼ N (Bt1 , t2 − t1 ), und somit gilt
Z Z
P[Bt1 ∈ A1 , Bt2 ∈ A2 ] =
p(t2 − t1 , x2 − x1 ) dx2 p(t1 , x1 ) dx1 .
A1
A2
Sei J = {t1 , . . . , tn } ⊂ R+ dann bezeichnen wir mit (t(1) , . . . , t(n) ) das Tupel der aufsteigend
angeordneten Elemente von J und wir bestimmen nach den obigen Überlegungen rekursiv
die Familie der endlich dimensionalen Verteilungen
PJ Bt1 ∈ A1 , . . . , Btn ∈ An =
Z
Z
Z
p(t(n) − t(n−1) , xn − xn−1 ) dxn p(t(n−1) − t(n−2) , xn−1 − xn−2 ) dxn−1 . . . p(t(1) , x1 ) dx1 .
...
A(1)
A(n−1)
A(n)
2.1. EXISTENZ DER BROWNSCHEN BEWEGUNG
19
Diese Familie ist offensichtlich projektiv, da der Ausdruck in der rechten Seite invariant
bezüglich Permutationen ist und es gilt
PJ Bt1 ∈ A1 , . . . , Btn ∈ R = PJ\{tn } Bt1 ∈ A1 , . . . , Btn−1 ∈ An−1 .
Aus dem Satz von Kolmogorov, Satz 1.1, folgt nun die Existenz eines eindeutigen stochastischen Prozesses B der die Bedingungen (a) und (b) erfüllt. Um schlussendlich die
Brownsche Bewegung zu erhalten müssen wir noch zeigen, dass dieser Prozess eine stetige
Modifikation besitzt. Damit ist dann die eindeutige Existenz eines Prozesses der zusätzlich
auch Eigenschaft (c) erfüllt bewiesen. Dazu bemühen wir das Kolmogorov-Centsov Stetigkeitskriterium, Satz 1.2. Da die Inkremente Bt − Bs einer N (0, |t − s|)-Verteilung folgen,
erhalten wir aus den bekannten Resultaten betreffend der Momente der Normalverteilung,
E|Bt − Bs |4 = 3|t − s|2
und somit sind die Bedingungen des Kriteriums erfüllt.
Als nächstes sammeln wir einige einfache Symmetrieeigenschaften der Brownschen Bewegung, sodass wir durch Transformationen eine Brownschen Bewegung wiederum Brownsche
Bewegungen erhalten. Im folgenden sei (Ω, F, P) ein Wahrscheinlichkeitsraum auf dem eine
Brownsche Bewegung B definiert ist.
Proposition 2.1. (i) (Symmetrie) Der Prozess −Bt , t ≥ 0, ist eine Brownsche Bewegung.
(ii) (Homogenität) Der Prozess Bs+t − Bs , t ≥ 0, ist für beliebiges s ≥ 0 eine Brownsche
Bewegung unabhängig von σ(Bu ; u ≤ s).
(iii) (Skalierung) Der Prozess cBt/c2 , t ≥ 0, ist für beliebiges c > 0 eine Brownsche Bewegung.
(iv) (Inversion) Der Prozess definiert durch X0 = 0 und Xt = tB1/t , t > 0, ist eine
Brownsche Bewegung.
Beweis. Die Eigenschaften (i)–(iii) sind klar und wir beweisen nur (iv). Aus der Definition gilt die Eigenschaft (a) der Brownschen Bewegung und wir betrachten die Inkremente
Xt − Xs . Diese sind normalverteilt, da die endlich-dimensionalen Verteilungen von B normalverteilt sind, mit E(Xt − Xs ) = 0 und
2
2
− 2tsEB1/t B1/s = t + s −
+ s2 EB1/s
E(Xt − Xs )2 = t2 EB1/t
2ts
= |t − s|.
max{t, s}
Daher sind die Inkremente stationär und ebenfalls durch Ausmultiplizieren der Kovarianz
folgt die Unabhängigkeit der Inkremente, da für t1 ≤ t2 ≤ t3 ≤ t4 gilt
E(Xt2 − Xt1 )(Xt4 − Xt3 ) =
t1 t3
t1 t4
t2 t3
t2 t4
+
−
−
= t2 + t1 − t1 − t2 = 0 .
t2 ∨ t4 t1 ∨ t3 t1 ∨ t4 t2 ∨ t3
20
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
Es bleibt die Stetigkeit der Pfade zu betrachten, wobei der einzig kritische Punkt an t = 0
ist. Da die Prozesse Xt , t ∈ (0, ∞) und Bt , t ∈ (0, ∞) dieselben endlich dimensionalen
Verteilungen besitzen gilt wegen limt→0, t∈Q+ Bt = 0 f.s. auch limt→0, t∈Q+ Xt = 0 f.s. . Da
aber Xt f.s. stetige Pfade auf (0, ∞) besitzt folgt auch limt→0, t∈R+ Xt = 0.
Die soeben bewiesene Eigenschaft der Inversion der Brownschen Bewegung liefert einen einfachen Beweis des folgenden starkes Gesetzes der Großen Zahlen, das sublineares Wachstum
der Brownschen Pfade liefert.
Korollar 2.1 (Starkes Gesetz der Großen Zahlen). Für eine Brownsche Bewegung B gilt
limt→∞
Bt
=0
t
f.s. .
Beweis. Wegen Prop. 2.1(iv) gilt 0 = lims→0 sB1/s = limt→∞ Bt /t f.s. wobei t = 1/s.
Bemerkung 2.3. Eine präzisere Beschreibung des lokalen Verhaltens von Brownschen Pfaden für t → ∞ und t → 0 liefert das Gesetz des iterierten Logarithmus und Lèvy’s modulus
of continuity. Diese Resultate werden wir aber nicht behandeln.
2.2
Pfadeigenschaften der Brownschen Bewegung
Als nächsten untersuchen wir Eigenschaften der Pfade der Brownschen Bewegung und
beginnen mit Eigenschaften, die das lokale Oszillationsverhalten betreffen.
Satz 2.2. (i) Eine Brownsche Bewegung besitzt endliche quadratische Variation und es
gilt
X
qm-lim|P[0,t] |→0
|Bti − Bti−1 |2 = t = L2[0,t] (B) .
i
(ii) Eine Brownsche Bewegung besitzt f.s. Pfade von unendlicher totaler Variation, d.h.,
X
1
V[0,t]
(B) = sup
|Bti − Bti−1 | = ∞ f.s. .
P[0,t]
i
(Genau genommen wird im Beweis nur gezeigt, dass die Menge der Pfade von endlicher totaler Variation in einer Nullmenge enthalten sind.)
Bemerkung 2.4. Der Quadratmittel Limes in (i) ist interpretiert als der Limes einer beliebigen Folge von Partitionen von [0, t], deren Feinheit gegen 0 konvergiert. Die Konvergenz
in (i) gilt fast sicher, falls die Folge
P der Partitionen aufsteigend ist (Pn ⊂ Pn+1 ) oder
der Radius genügend schnell fällt ( n |Pn | < ∞) . Die Eigenschaft (ii) erlaubt nun nicht
mehr ein Integral bezüglich einer Brownschen Bewegung pfadweise im Sinne des RiemannStieltjes Integral zu definieren und ist der Grund für die Entwicklung einer stochastischen
Integrationstheorie in der die Rolle der “klassischen” Variation (ii) durch die quadratische
Variation in (i) ersetzt wird. Die Resultate gelten natürlich analog für beliebige endliche
Intervall [a, b] und resultierender quadratischer Variation b − a.
2.2. PFADEIGENSCHAFTEN DER BROWNSCHEN BEWEGUNG
21
Beweis. (i) Wegen der Unabhängigkeit der Inkremente und da EZ 4 = 3EZ 2 für normalverteiltes Z gilt
hX
i2
hX
i2
(Bti − Bti−1 )2 − (ti − ti1 )
E
(Bti − Bti−1 )2 − t
= E
i
i
i2
X h
2
=
E (Bti − Bti−1 ) − (ti − ti1 )
(unabhängige Inkremente)
i
≤ 2
X
E(Bti − Bti−1 )4 + 2
i
X
≤ 8
(ti − ti−1 )2
X
(ti − ti1 )2
i
i
≤ 8t |P[0,t] |
und die Aussage folgt da |P[0,t] | → 0.
(ii) Konvergenz im Quadratmittel impliziert Konvergenz in der Wahrscheinlichkeit und
diese wiederum impliziert, es existiert eine Teilfolge die fast sicher konvergiert. Sei nun
n
P[0,t]
ein Folge von Partitionen, sodass
lim
|P[0,t] |→0
X
|Bti (ω) − Bti−1 (ω)|2 = t
(∗)
i
für alle ω ∈ Ω0 ∈ F mit P(Ω0 ) = 1 und o.B.d.A. können wir annehmen, dass alle diese
Pfade stetig sind. Dann gilt
X
X
2
|Bti (ω)−Bti−1 (ω)| ≤ sup |Bti (ω)−Bti−1 (ω)| sup
|Bti (ω)−Bti−1 (ω)| ∀ ω ∈ Ω0 .
i
i
P[0,t]
i
Ist nun die totale Variation endlich, dann konvergiert wegen der Stetigkeit der Brownschen
Pfade die obere Schranke gegen null. Dies ist ein Widerspruch zu (∗) und daher muss die
totale Variation auf Ω0 unendlich sein.
Satz 2.3. Eine Brownschen Bewegung besitzt f.s. lokal Hölder-stetige Pfade mit Hölderexponent γ < 1/2 und ist f.s. nirgends lokal Hölder-stetig mit Exponent γ > 1/2. Genauer
ausgedrückt gilt die zum Exponent γ > 1/2 an einem Punkt lokal Hölder-stetigen Pfade
sind in einer Nullmenge enthalten.
Beweis. Der erste Teil des Satzes folgt wie schon die Stetigkeit aus dem Satz von KolmogorovCentsov, Satz 1.2. Da die Inkrement normalverteilt sind existiert für jedes p > 0 eine
Konstante Cp , sodass
E|Bt − Bs |2p = Cp |t − s|p .
Daher sind die Pfade lokal Hölder-stetig für alle γ < (p − 1)/(2p) = 1/2 − 1/(2p). Da p
beliebig groß gewählt werden kann folgt die f.s. lokale Hölder-stetigkeit für alle γ < 1/2.
22
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
Der zweite Teil des Satzes ist analog zum Beweis von Satz 2.2(ii). Sei wieder um P[0,t] ein
Folge von Partitionen, sodass
X
lim
|Bti (ω) − Bti−1 (ω)|2 = t
(∗)
|P[0,t] |→0
i
für alle ω ∈ Ω0 mit P(Ω0 ) = 1. Falls |Bs1 (ω) − Bs2 (ω)| ≤ K|s1 − s2 |γ für alle s1 , s2 ≤ t und
ein γ > 1/2, dann gilt
X
|Bti (ω) − Bti−1 (ω)|2 ≤
X
i
i
K 2 |ti − ti−1 |2γ ≤ K 2 t sup |ti − ti−1 |2γ−1 .
i
Da |P[0,t] | → 0 konvergiert die rechte Seite gegen null. Wiederum erhalten wir einen Widerspruch zu (∗) und es folgt, die Pfade sind fast sicher nicht Hölder-stetig mit Exponent
γ > 1/2 auf [0, t]. Dasselbe Argument lässt sich nun für beliebige Intervalle wiederholen
und dies impliziert, dass die Brownsche Bewegung f.s. nirgends lokal Hölder-stetig mit
Exponent γ > 1/2 ist.
Bemerkung 2.5. Der obige Satz lässt die lokale Hölder-Stetigkeit für den Fall γ = 12 unbeantwortet. Das Gesetz des iterierten Logarithmus impliziert, dass der Pfad nicht überall
lokal Hölder-stetig mit Exponent γ = 1/2 sein kann. Dies heißt aber nicht, dass ein solcher Pfad diese Eigenschaft nirgends auf [0, ∞) haben kann. Eine detailliertere Diskussion
dieses Aspekts findet sich in [KS91, S. 113].
Schlussendlich zeigen wir noch, dass die Pfade eine Brownschen Bewegung fast sicher nirgends differenzierbar sind. Die umständliche Formulierung des Satzes trägt dem Umstand
Rechnung, dass nicht bekannt ist, ob die Menge der an einem Punkt differenzierbaren Pfade
messbar ist.
Satz 2.4. Die Menge der an einem Punkt differenzierbaren Pfade einer Brownschen Bewegung sind in einer Nullmenge enthalten.
Beweis. Es ist ausreichend, Brownsche Pfade über den Intervall [0, 1] zu betrachten, da
abzählbare Vereinigungen von Nullmengen wieder um Nullmengen sind. Wir definieren
(t)
D+ f (t) = lim suph↓0 f (t+h)−f
und bezeichnen analog mit D+ f (t) den Limes inferior.
h
Klarerweise gilt, ist f differenzierbar an t dann ist −∞ < D+ f (t) = D+ f (t) < ∞. Wir
betrachten nun die Menge
C := ω ∈ Ω : −∞ < D+ Bt (ω) ≤ D+ Bt (ω) < ∞ für ein t ∈ [0, 1] ,
die alle an einer Stelle t ∈ [0, 1] differenzierbaren Brownschen Pfade enthält, und zeigen,
dass C in einer Nullmenge liegt. Wir definieren weiters die Mengen
[
\ Ajk :=
ω ∈ Ω : |Bt+h (ω) − Bt (ω)| ≤ jh ,
j, k ∈ N,
t∈[0,1] h∈[0,1/k]
2.2. PFADEIGENSCHAFTEN DER BROWNSCHEN BEWEGUNG
und es gilt
C⊆
∞ [
∞
[
23
Ajk
(∗)
j=1 k=1
aus folgendem Grund: Sei t so, dass für eine Pfad ω ∈ C gilt −∞ < D+ Bt (ω) und
D+ Bt (ω) < ∞, d.h., für alle h klein genug, z.B., für alle h ≤ 1/k mit k groß, gilt, dann
existieren reelle Konstanten C ± mit
Bt+h (ω) − Bt (ω)
≤ C+
h
und C − ≤
Bt+h (ω) − Bt (ω)
h
für h klein und somit gilt
hC − ≤ Bt+h (ω) − Bt (ω) ≤ hC +
⇒
|Bt+h (ω) − Bt (ω)| ≤ h max{|C − |, |C + |}.
Es folgt nun dieser Pfad ω liegt in Ajk für große j und k. Die Inklusion (∗) folgt. Auf Grund
dieser reicht es nun aber für den Beweis des Satzes aus zu zeigen, dass für alle j, k ∈ N eine
Nullmenge C ∈ F, d.h., P(C) = 0, existiert, die Ajk enthält, da abzählbare Vereinigungen
von Nullmengen wiederum Nullmengen sind.
Wir wählen j, k fix und fixieren einen bestimmten Pfad ω ∈ Ajk . Für diesen gilt
∃ t ∈ [0, 1] :
|Bt+h (ω) − Bt (ω)| ≤ jh
∀ h ∈ [0, 1/k] .
(∗∗)
Ein derartiges t sei nun ebenfalls fix und wir wählen ein n ≥ 4k. Dann können wir eine
natürliche Zahl i in {1, . . . , n} so wählen, dass
i−1
i
≤t≤
n
n
und somit
i+m
m+1
1
−t≤
≤
n
n
k
für m = 0, 1, 2, 3 .
(∗ ∗ ∗)
Wir benutzen (∗∗) und (∗ ∗ ∗) und erhalten
|B(i+1)/n (ω) − Bi/n (ω)| ≤ |B(i+1)/n (ω) − Bt (ω)| + |Bi/n (ω) − Bt (ω)|
i + 1
i
≤
−t j+
−t j
n
n
2j
j
≤
+ .
n
n
Wichtig ist nun, dass wir durch ω ∈ Ajk nicht nur die Inkremente über [i/n, (i + 1)/n]
sondern auch über die nachfolgenden Intervalle [(i+1)/n, (i+2)/n] und [(i+2)/n, (i+3)/n]
erhalten. Dieselbe Abschätzung wie zuvor ergibt wegen (∗∗) und (∗ ∗ ∗), dass
|B(i+2)/n (ω) − B(i+1)/n (ω)| ≤ |B(i+2)/n (ω) − Bt (ω)| + |B(i+1)/n (ω) − Bt (ω)| ≤
3j 2j
+
n
n
und
|B(i+3)/n (ω) − B(i+3)/n (ω)| ≤ |B(i+3)/n (ω) − Bt (ω)| + |B(i+2)/n (ω) − Bt (ω)| ≤
4j 3j
+
.
n
n
24
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
Damit haben wir gezeigt, dass mit
(n)
Ci
:=
3
[
ω ∈ Ω : |B(i+m)/n (ω) − B(i+m−1)/n (ω)| ≤ (2m + 1)j/n
m=1
Sn
(n)
(n)
gilt Ajk ∈ i=1 Ci falls n ≥ 4k. Klarerweise gilt Ci ∈ F, da die Elemente nur von
endlich vielen Koordinaten abhängen. Nun gilt aber, dass
√
n (B(i+m)/n − B(i+m−1)/n ) ∼ u.i.v. N (0, 1)
und, da für Z ∼ N (0, 1) gilt P[|Z| ≤ δ] ≤ δ, folgt
(n)
P(Ci )
3
h√
Y
=
P n|B(i+m)/n − B(i+m−1)/n | ≤
m=1
Wählt man nun C als
C :=
n
∞ [
\
(n)
Ci
(2m+1)j
√
n
i
105j 3
≤ 3/2 .
n
∈ F,
n=4k i=1
dann gilt Ajk ∈ C. Der Beweis ist nun abgeschlossen, da
n
[
105j 3
(n)
P(C) ≤ inf n≥4k P
Ci
≤ inf n≥4k 3/2 = 0 .
n
i=1
2.3
Verwandte Prozesse
In diesem Abschnitt betrachten wir kurz einige weitere wichtige stochastische Prozesse, die
sich aus der Brownschen Bewegung ergeben. Die Pfade der besprochenen Prozesse sind in
Abbildung 2.1 illustriert.
Beispiel 2.1 (Brownsche Bewegung in x). Der Prozess Xt = x + Bt , t ≥ 0, heißt Brownsche
Bewegung in x. Da die Bedingung B0 = 0 nicht immer Teil der Definition einer Brownschen
Bewegung ist, heißt B auch standard Brownsche Bewegung.
Beispiel 2.2 (Brownsche Brücke). Der Prozess Xt = Bt − tB1 definiert für t ∈ [0, 1] heißt
Brownsche Brücke. Er besitzt offensichtlich stetige Pfade und erfüllt X0 = X1 = 0 fast
sicher.
Beispiel 2.3 (Ornstein-Uhlenbeck Prozess). Ein Prozess X definiert als
√
Xt = c e−βt Bexp(2βt) , t ≥ 0
mit c, β > 0
heißt Ornstein-Uhlenbeck Prozess. Der Ornstein-Uhlenbeck Prozess ist – im Gegensatz zur
Brownschen Bewegung – stationär.
2.3. VERWANDTE PROZESSE
25
Brownsche Bewegung
Brownsche Brücke
3
1.5
2
1
1
0.5
0
0
−1
−0.5
−2
−1
−3
0
0.2
0.4
0.6
0.8
1
−1.5
0
t
Ornstein−Uhlenbeck Prozess
4
0.2
0.4
0.6
0.8
t
Geometrische Brownsche Bewegung
1
0.4
1
5
(c=1,β=1)
(µ=0,σ=1)
4
2
3
0
2
−2
−4
1
0
0.2
0.4
0.6
0.8
1
0
0
t
Geometrische Brownsche Bewegung
15
0.6
0.8
t
Geometrische Brownsche Bewegung
1.5
(µ=2,σ=1)
(µ=−2,σ=1)
10
1
5
0.5
0
0.2
0
0.2
0.4
0.6
t
0.8
1
0
0
0.2
0.4
0.6
0.8
1
t
Abbildung 2.1: Jeweils 10 Pfade verschiedener, in diesem Kapitel besprochener Prozesse.
26
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
Beispiel 2.4 (Geometrische Brownsche Bewegung). Ein Prozess X definiert als
2
Xt = c exp µ − σ /2 t − σBt , t ≥ 0
mit c, µ, σ ∈ R
heißt geometrische Brownsche Bewegung. Er besitzt für c > 0, bzw., c < 0, positive bzw.
negative Pfade. Die wichtigste Anwendung ist in der Finanzmathematik als einfachster
Preisprozess, vgl. Black-Scholes Modell.
Bemerkung 2.6. Der Ornstein-Uhlenbeck Prozess und die geometrische Brownsche Bewegung lösen gewisse stochastische Differentialgleichungen. Speziell gilt, die Lösungen zu
skalaren, linearen stochastischen Differentialgleichungen mit additiven bzw. linearen multiplikativen Wiener Rauschen sind Versionen der Prozesse definiert in Beispiel 2.3 bzw. 2.4.
Die meisten der Prozesse, die wir bis jetzt betrachtet haben besitzen die Eigenschaft, dass
ihre endlich-dimensionalen Verteilungen Normalverteilungen sind. Daher sind sie Beispiele
für die folgende Klasse von stochastischen Prozessen.
Definition 2.1. Ein stochastischer Prozess X heißt Gaussprozess, falls seine endlichdimensionalen Verteilungen eine Familie von Normalverteilungen ist, d.h., jeder endliche
Vektor (Xt1 , . . . , Xtn ), n ∈ N und t1 , . . . , tn ∈ I, besitzt eine n-dimensionale Normalverteilung.
Bekanntermaßen sind Normalverteilungen durch ihre ersten beiden Momente eindeutig
festgelegt und ähnliches gilt auch für Gaussprozesse. Wir bezeichnen mit
t 7→ m(t) := EXt
und (s, t) 7→ K(s, t) := E(Xs − m(s))(Xt − m(t))
die Mittelwert- und die Kovarianzfunktion eines Prozesses. Ein Prozess heißt zentriert falls
m(t) = 0 für all P
t ≥ 0. Es gilt, die Kovarianzfunktion eines Gaussprozesses ist positiv
semidefinit, d.h., ni,j=1 K(ti , tj )ai aj ≥ 0 für alle ti , . . . , tn ∈ I und alle a1 , . . . , an ∈ R.
Dies folgt da die Kovarianzmatrix einer Normalverteilung positiv semidefinit ist. Der folgende Satz liefert nun die Charakterisierung von Gaussprozessen aus ihrer Mittelwert- und
Kovarianzfunktion.
Satz 2.5. Zu jeder Mittelwertfunktion m und jeder positiv semidefiniten Kovarianzfunktion
K existiert ein (bis auf Versionen) eindeutiger Gaussprozess.
Beweis. Da m + X ein eindeutiger Gaussprozess mit Mittelwertfunktion m und K ist,
falls X der eindeutige zentrierte Gaussprozess mit Kovarianz K ist, ist es ausreichend die
Existenz und Eindeutigkeit von zentrierten Gaussprozessen zu zeigen. Dazu verwenden wir
den Satz von Kolmogorov, d.h., die Aufgabe ist es aus Kovarianzfunktion eine eindeutige
projektive Familie von Verteilungen zu konstruieren. Da diese bei Gaussprozessen eine
Familie von zentrierten Gaussverteilungen ist, müssen wir nur deren Kovarianzmatrizen
eindeutig bestimmen.
Zu je endlich-vielen Indices t1 , . . . , tn ∈ I konstruieren wir mittels der Kovarianzfunktion
eiPn
ne Matrix (σij )i,j=1,...,n mit σij := K(ti , tj ). Diese ist positiv semidefinit, d.h., i,j=1 σij ai aj
2.3. VERWANDTE PROZESSE
27
Gauss‘sches Weißes Rauschen
Gauss‘sches Weißes Rauschen
4
4
2
2
0
0
−2
−2
−4
0
0.2
0.4
0.6
t
0.8
1
−4
0
0.2
0.4
0.6
0.8
1
t
Abbildung 2.2: Illustration zweier Pfade von Gauss’schem Weißen Rauschen. Beachte, die
Pfade des Prozesses sind eigentlich nicht stetig.
für alle a1 , . . . , an ∈ R, da K positiv semidefinit ist. Die Matrix definiert eine eindeutige,
zentrierte Normalverteilung. Somit, definiert die Kovarianzfunktion eindeutig die Familie
der endlich-dimensionalen Verteilungen. Das diese Familie endlich-dimensionaler Verteilungen projektiv ist, folgt analog zu den Argumenten im Existenzsatz zur Brownschen
Bewegung, Satz 2.1, und der Beweis ist abgeschlossen.
Aus diesem Satz folgt nun eine zweite Charakterisierung der Brownschen Bewegung: Die
Brownsche Bewegung ist der eindeutige f.s. stetige, zentrierte Gaussprozess zur Kovarianzfunktion K(s, t) = s ∧ t . Die Existenz des Prozesses folgt aus Satz 2.5, die Unabhängigkeit
der Inkremente folgt aus der Kovarianzfunktion, da im Falle von Normalverteilungen Unkorreliertheit und Unabhängigkeit äquivalent sind, und die Existenz einer stetigen Modifikation folgt auch hier wiederum aus dem Satz von Kolmogorov-Centsov.
Analoges gilt auch für die oben beschriebenen Prozesse. So ist die Brownsche Bewegung
gestartet in x die stetige Version des Gaussprozesses zur Kovarianzfunktion K(s, t) = s ∧ t
und Mittelwertfunktion m(t) = x, der Ornstein-Uhlenbeck Prozess die stetige Version des
zentrierten Gausprozesses zu K(s, t) = c exp(−β|t − s|) und die Brownsche Brücke ist
die stetige Version des zentrierten Gaussprozesses auf [0, 1] definiert durch die Kovarianz
K(s, t) = s(1 − t) für s ≤ t. Klarerweise ist aber die geometrische Brownsche Bewegung
kein Gaussprozess, da die eindimensionale Verteilungen log-Normalverteilungen sind.
Weitere wichtige Beispiele von Gaussprozessen sind die folgenden stochastischen Prozesse.
Beispiel 2.5 (Fraktionale Brownsche Bewegung). Der zentrierter, stetige Gaussprozess X
zur Kovarianzfunktion
1 2H
2H
2H
,
K(s, t) =
t + s + |t − s|
2
mit H ∈ (0, 1), heißt Fraktionale Brownsche Bewegung. Für H = 1/2 stimmt die Fraktionale Brownsche Bewegung mit der Brownschen Bewegung überein. Die Konstante H heißt
Hurst Parameter des Prozesses und ist ein Mass für das Langzeitgedächtnis des Prozesses.
28
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
Beispiel 2.6 (Gauss’sches Weißes Rauschen). Wir betrachten den zentrierten Gaussprozess
X, der durch die Kovarianzfunktion K(s, t) = I[t=s] definiert ist. Dieser heißt Gauss’sches
Weißes Rauschen. Gauss’sches Weißes Rauchen besitzt keine guten Eigenschaften, nicht
einmal eine messbare (und somit auch keine f.s. stetige) Version existiert. Gauss’sches
Weißes Rauschen ist die Ableitung der Brownschen Bewegung im Sinne von Distributionen.
2.4
Reihenentwicklung der Brownschen Bewegung
Im folgenden beschränken wir uns auf Prozesse über der Indexmenge [0, 1], aber die Ergebnisse sind klarerweise ohne Einschränkung für beliebige endliche Indexmengen [a, b] ∈ R+
gültig. Weiters erhalten wir Prozesse auf R+ durch Aneinaderfügen von Ergebnissen auf
endlichen Intervallen.
2.4.1
Satz von Levy-Ciesielski und die Paley-Wiener Entwicklung
Gegeben sei ein Wahrscheinlichkeitsraum (Ω, F, P) mit einer darauf definierten Folge von
unabhängigen, standard normalverteilten Zufallsvariablen ξn , n ∈ N. Der folgende Satz
liefert Reihendarstellungen von Brownschen Bewegungen in dem Sinne, das eine Brownsche
Bewegung der Limes einer zufällig gewichteten Funktionenreihe ist. Weiters liefert der Satz
eine alternative Methode um die Existenz einer Brownschen Bewegung zu erhalten bei der
wir die Schwierigkeiten im Zusammenhang mit kanonischen Wahrscheinlichkeitsräumen
aus überabzählbaren Produkträumen vermeiden.
Satz 2.6 (Levy-Ciesielski). Sei ξn , n ∈ N, eine Folge unabhängig, standard normalverteilter Zufallsvariablen und ϕn , n ∈ N, eine Orthonormalbasis (ONB) von L2 (0, 1). Dann
konvergiert die Summe
Z t
∞
X
Bt =
ξn
ϕn (s) ds
n=1
0
fast sicher in C[0, 1] und B ist eine Brownsche Bewegung auf [0, 1].
Bemerkung 2.7. Durch Aneinanderfügen von unabhängigen Brownschen Bewegungen auf
[0, 1] erhält man sofort die Existenz einer Brownschen Bewegung auf R+ . Im Unterschied
zum ersten Existenzbeweis mittels des Satz von Kolmogorov in Satz 2.1, der eine reine Existenzaussage ist, ist dieser Beweis tatsächlich eine Konstruktion einer Brownschen
Bewegung. Die Umkehrung des Satzes - die Existenz einer Zerlegung zu gegebener Brownschen Bewegung mit obigen Eigenschaften und die Konvergenz - ist einfacher zu zeigen.
Die Zerlegung im Satz 2.6 heißt einfach orthogonal, da die ξn orthonormal im√Raum der
quadrat-integrierbaren Zufallsvariablen sind. Für die Wahl der ONB ϕn (t) = 2 sin(nπt)
entspricht dieses Resultat (nicht die Beweistechnik) dem ursprünglichen Existenzbeweis der
Brownschen Bewegung von N. Wiener. Ein Spezialfall dieses Satzes ist die Paley-Wiener
Entwicklung der Brownsche Bewegung:
X Z t
X e2inπt − 1
e2inπs ds
ξn =
ξn
Bt =
2inπ
0
n∈Z
n∈Z
2.4. REIHENENTWICKLUNG DER BROWNSCHEN BEWEGUNG
29
0.4
0.2
0
−0.2
−0.4
−0.6
N=5
N=10
N=20
n=40
N=1000
−0.8
−1
0
0.1
0.2
0.3
0.4
0.5
t
0.6
0.7
0.8
0.9
1
Abbildung
√ 2.3: Approximation eines Brownschen Pfades mittels Satzes 2.6 aus der ONB
ϕn (t) = 2 sin(nπt) durch endliche Reihen mit N Summanden.
mit ONB (e2inπt )n∈Z . Meist wird in modernen Büchern zum Beweis der Existenz eine ONB
(n)
mittels der Haar’schen Funktionen Hk , n ≥ 0 und k ≤ 2n mit k ungerade, gewählt, wobei
(0)
H1 (t) = 1, t ∈ [0, 1], und
 (n−1)/2
für k−1
≤ t < 2kn ,

2n
 2
(n)
Hk (t) =
2(n−1)/2 für 2kn ≤ t < k+1
,
2n


0 sonst.
Bei dieser Wahl einer ONB konvergiert die Summe in Satz 2.6 sogar f.s. punktweise absolut
was die Beweisführung erleichtert. Die Integrale von Haar’schen Funktionen, die in der
Reihenentwicklung auftreten, sind die Schauderfunktionen.
Beweis. Im Beweis benutzen wir folgende Resultate der Theorie unendlicher Summen unabhängigen Zufallsvariablen. Erstens, verwenden wir den Satz von Itô-Nisio: In einem separablen Banachraum ist die fast sichere Konvergenz einer unendlichen Summe unabhängiger
30
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
Zufallsvariablen äquivalent zur Konvergenz in Wahrscheinlichkeit. Für reelle, zentrierte unabhängige Zufallsvariable ist die Konvergenz der Summe der Varianzen eine hinreichende
Bedingung für die Konvergenz der Summe von Zufallsvariablen. Weiters ist dann die unendliche Summe ebenfalls eine f.s. endliche Zufallsvariable. Schlussendlich ist klarerweise
ein konvergente Reihe normalverteilter Zufallsvariablen wiederum normalverteilt und der
Erwartungswert und die Varianz sind durch die Summe der Erwartungswerte und Varianzen gegeben.
(i) Konvergenz der Summe: Wir definieren für Funktionen f auf [0, 1] für alle α ∈ (0, 1]
den linearen Operator
Z t
α
D f (t) :=
Γ−1 (α)(t − s)α−1 f (s) ds
und somit Bt =
–
0
P∞
n=1 ξn
D1 ϕn (t). Für diese Operatoren gilt
Dβ+α = Dβ Dα , da wegen dem Assoziativgesetz für Faltungen gilt
Dβ Dα f = kβ ∗ (kα ∗ f ) = (kβ ∗ kα ) ∗ f
mit kα (s) = Γ−1 (α)sα−1 . Mittels Substitution s = tr ist sofort ersichtlich, dass
Z t
1
(kβ ∗ kα )(t) =
(t − s)β−1 sα−1 ds
Γ(α)Γ(β) 0
Z 1
tβ+α−1
(1 − r)β−1 rα−1 dr
=
Γ(α)Γ(β) 0
= Γ−1 (β + α) tβ+α−1 .
–
Dα , α > 12 , ist ein stetiger Operator L2 (0, 1) → Lp (0, 1), p < ∞, da
Z 1Z t
p
p
α
−1
α−1
kD f kLp =
Γ (α)(t − s) f (s) ds dt
Z0 1 Z 0t
p/2 Z t
p/2
−1
α−1 2
(Cauchy-Schwarz Ungl.) ≤
Γ (α)(t − s)
ds
f 2 (s) ds
dt
0
≤
–
0
0
cα,p kf kpL2
.
Dβ , β > p1 , ist ein stetiger Operator Lp (0, 1) → C[0, 1], da
Z t
−1
β−1
β
Γ (α)(t − s) f (s) ds
kD f k0 = sup t∈[0,1]
(Hölder Ungl., p
−1
+q
−1
= 1) ≤
Z
1
0
−1
|Γ (α)(t − s)
0
≤ c0β,p kf kLp .
| ds
α−1 q
1/q Z
1
1/p
|f (s)| ds
p
0
2.4. REIHENENTWICKLUNG DER BROWNSCHEN BEWEGUNG
31
Unter Verwendung dieser Operatoren mit 2 < p < ∞, α > 12 , β > p1 und α + β = 1 folgt
aus der Markov Ungleichung, dass
∞
m
∞
m
hX
i
X
p
X
X
1 P ξn D1 ϕn −
ξn D1 ϕn ≥ ≤ p EDβ
ξn Dα ϕn −
ξn Dα ϕn 0
0
n=1
n=1
n=1
n=1
∞
m
p
X
c0β,p X
α
α
E
ξ
D
ϕ
−
ξ
D
ϕ
≤
p.
n
n
n
n
p
L
n=1
n=1
Angenommen die Konvergenz der letzten Summe hält im p-ten Mittel in Lp (0, 1), dann
erhalten wir die Konvergenz in Wahrscheinlichkeit von B in C[0, 1] und, da C[0, 1] ein
separabler Banachraum ist, aus dem Satz von Itô-Nisio P
die fast sichere Konvergenz. Daher
α
p
reicht es im Folgenden aus, die Konvergenz der Reihe ∞
n=1 ξn D ϕn in L (0, 1) im p-ten
Mittel zu beweisen.
P
α
Wir zeigen nun zuerst, dass für jedes t ∈ [0, 1] die Summe ∞
n=1 ξn D ϕn (t) f.s. konvergiert.
Klarerweise ist dann diese Summe zentriert normalverteilt mit Varianz gleich der Summe
der Varianzen. Laut oben zitierten Resultat müssen wir dazu nur zeigen, dass die Summe
der Varianzen konvergiert:
∞
∞ Z 1
X
X
2 1/2
2 1/2
α
D ϕn (t)
=
Γ−1 (α)(t − s)α−1 ϕn (s)I[0,t) (s) ds
n=1
n=1
1
Z
0
2 1/2
Γ−1 (α)(t − s)α−1 I[0,t) (s) ds
0
Z t
1/2
−1
2α−2
= Γ (α)
(t − s)
ds
(Parseval Gleichung) =
0
α−1/2
t
Γ(α)(2α − 1)1/2
1
≤
.
Γ(α)(2α − 1)1/2
=
(∗)
Aus der Normalverteilung dieser Zufallsvariablen folgt nun auch, dass die p-ten Momente
von Bt in t beschränkt sind, denn
∞
∞
X
p
X
2 p/2
E
Dα ϕn (t)ξn =
Dα ϕn (t)
E|Y |p ≤ C < ∞
(∗∗)
n=1
n=1
mit Y ∼ N (0, 1) und die obere Schranke C kann wegen der Abschätzung (∗) unäbhängig
von t ∈ [0, 1] gewählt
Mittels des Satzes von Fubini – die gemeinsame Messbarkeit
P werden.
α
D
ϕ
folgt, da (ω, t) 7→ ∞
n (t)ξn (ω) eine Carathéodory-Funktion ist – und des Satzes
n=1
von der Dominierten Konvergenz – dominiert durch (∗∗) – können wir nun punktweise
Konvergenz von Bt im p-ten Mittel zur Konvergenz im p-ten Mittel von B in Lp (0, 1)
ausdehnen:
Z 1 X
Z 1 X
∞
∞
∞
p
X
p
2 p/2
p
α
α
dt < ∞ .
E
ξn D ϕn (t) dt = E|Y |
Dα ϕn (t)
E
ξn D ϕn =
n=1
Lp
0
n=1
0
n=1
32
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
Somit erhalten wir das die Folge der Partialsummen in der Norm in Lp (0, 1) im p-ten Mittel
gegen eine Lp (0, 1)-wertige Zufallsvariable konvergiert, die wir mit der unendlichen Summe
bezeichnen.
Wir haben nun die Existenz des Prozesses B im Satz 2.6 gezeigt. Es bleibt noch zu zeigen,
dass dieser Prozess eine Brownsche Bewegung ist. Klarerweise gilt, dass B f.s. stetig ist, da
B f.s. der gleichmässige Limes stetiger Funktionen auf einem kompakten Intervall ist. Dies
erhält die Stetigkeit für die Grenzfunktion. Um den Beweis abzuschließen reicht es also die
Kovarianz der Brownschen Bewegung zu zeigen, die ja die Unabhängigkeit der Inkremente
impliziert.
(ii) Kovarianzfunktion: Da die Reihe in C[0, 1] f.s. konvergiert und somit auch punktweise
f.s. konvergiert, gilt, dass für fixes t die Summe zentriert normalverteilt ist mit Varianz
gleich Summe der Varianzen, d.h., mittels der Parseval Gleichung
∞ Z t
∞
2
X
X
2
2
EBt =
ϕn (s) ds =
ϕn , I[0,t] L2 = kI[0,t] k2L2 = t .
n=1
0
n=1
Daher bleibt nur noch die Kovarianz zu zeigen. Zur Vertauschung der Erwartungswertes
und der unendlichen Summe mittels des Satzes A.3 benötigen wir die gleichgradige Integrierbarkeit der Zufallsvariablen Btn Bsn , n ∈ N, t, s ∈ [0, 1]. Diese folgt wegen Satz A.2 aus
der Abschätzung
E(Btn Bsn )2 ≤
1
1
1
1
E|Btn |2 + E|Bsn |2 ≤ E|Bt |2 + E|Bs |2 ≤ 1
2
2
2
2
und daraus resultierender gleichmässiger Beschränktheit der zweiten Momente. Daher gilt
Z t
Z s
∞
∞
X
X
EBt Bs = E
ξn
ϕn (r) dr
ξn
ϕn (r) dr
= E
=
n=1
∞
X
0
Z
ξn ξm
n,m=1
∞
XZ 1
Z
t
ϕm (r) dr
0
ϕn (r) I[0,t] (r) dr
s
ϕn (r) dr
0
n=1
1
Z
0
n=1
0
Z
1
ϕn (r) I[0,t] (r) dr
0
I[0,t] (r) I[0,s] (r) dr
(Parseval Gleichung) =
0
= t ∧ s.
2.4.2
Karhunen-Loève Entwicklung
Eine weitere Reihendarstellung einer Brownschen Bewegung, oder auch allgemeinerer stochastischer Prozesse, erhält man wenn man pfadweise deren Fourierentwicklung betrachtet.
2.4. REIHENENTWICKLUNG DER BROWNSCHEN BEWEGUNG
33
Im folgenden Rsei X ein quadrat-integrierbarer, messbarer reeller Prozess mit Indexmenge
1
[0, 1], sodass 0 EXt2 dt < ∞. Somit gilt wegen des Satzes von Fubini auch X ∈ L2 (0, 1)
fast sicher.
Sei nun ϕ
bn , n ∈ N, eine ONB in L2 (0, 1). Dann ist für fast alle Pfade die FourierreihenDarstellung
∞ Z 1
X
b
Xt (ω) :=
Xs (ω) ϕ
bn (s) ds ϕ
bn (t)
(2.1)
n=1
0
b L2 = 0 fast sicher. Unter gewissen Bedingungen an die Pfadefiniert und es gilt kX − Xk
de von X und / oder die gewählte ONB kann man auch fast sichere punktweise und
bt − Xt | = 0 für alle t ∈ [0, 1] fast sicher
fast sichere glm. Konvergenz zeigen, d.h., |X
bt − Xt | fast sicher. Die Art der Konvergenz der Funktionenfolge für fixes
bzw. supt∈[0,1] |X
ω interessiert uns hier im Folgenden aber nicht mehr, dies ist eine Problemstellung in der
Fourieranalysis und nicht der Stochastik. Uns interessiert in welchem Sinne die stochastische Gleichheit gilt. Bedenke, die fast sichere Konvergenz impliziert im Allgemeinen nicht
b L2 6= 0.
die Konvergenz im Erwartungswert impliziert, d.h., unter Umständen gilt EkX − Xk
Weiters, ist es für eine Reihendarstellung von Vorteil, z. B., zu Simulationszwecken, dass
die Korrelationsstruktur und die gemeinsame Verteilung der stochastischen Fourierkoeffizienten bestimmt werden kann.
Der folgende Satz von Karhunen-Loéve gibt Auskunft darüber welchem, basierend auf der
Kovarianz des Prozesses, die optimale ONB für Fourierentwicklung ist, d .h., er gibt eine
ONB an, sodass die Fourierkoeffizienten unkorreliert sind und weiters der Quadratmittelfehler minimiert wird und man somit die beste Approximation durch Partialsummen
erhält. Zum Beweis des Satzes brauchen wir noch folgenden Satz aus der Analysis.
Satz 2.7 (Satz von Mercer). Die Abbildung K : [0, 1] × [0, 1] → R sei stetig, symmetrisch,
d.h., K(s, t) = K(t, s) für alle t, s ∈ [0, 1], und positiv semi-definit. Dann existiert eine
Orthonormalbasis (ϕn )n∈N von L2 (0, 1) bestehend aus Eigenfunktionen des Integraloperators
TK : L2 (0, 1) → L2 (0, 1) definiert mittels
Z 1
(TK f )(s) :=
K(s, t)f (t) dt
0
und die dazugehörigen Eigenwerte λn , n ∈ N, sind nicht-negativ. Weiters gilt, die Eigenfunktion zu positiven Eigenwerten sind stetig und es gilt
X
K(s, t) =
λn ϕn (s)ϕn (t)
n∈N
und diese Summe konvergiert gleichmässig und absolut.
Eine Abbildung K heißt Kern des durch sie definierten Integraloperators TK und ein Kern,
der die Bedingung des Satzes von Mercer erfüllt heißt Mercer-Kern. Die Karhunen-Loève
Zerlegung ist nun eine optimale Fourier-Entwicklung eines stochastischen Prozesses, dessen
Kovarianzfunktion ein Mercer-Kern ist.
34
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
Satz 2.8 (Karhunen-Loève Entwicklung). Sei X = (Xt )t∈[0,1] ein zentrierter1 , quadratintegrierbarer stochastischer Prozess mit stetiger Kovarianzfunktion KX . Dann gilt
(i) KX ist ein Mercer-Kern und ϕn , n ∈ N, sei eine ONB von L2 (0, 1) wie im Satz von
Mercer mit den dazugehörigen Eigenwerten λn , n ∈ N;
(ii) die Zufallsvariablen
Z
Zn :=
t
Xs ϕn (s) ds
0
sind zentriert, besitzen Varianz λn und sind paarweise unkorreliert, d.h.,
EZn = 0,
EZn Zm = δnm λn
∀ m, n ∈ N ;
(iii) die Karhunen-Loève Zerlegung
Xt =
∞
X
Zn ϕn (t) ,
n=1
gilt im Quadratmittel und ist gleichmässig in t, d.h.,
n
2
X
lim sup EXt −
Zn ϕn (t) = 0 ;
n→∞ t∈[0,1]
i=1
(iv) Unter allen Reihendarstellungen der Form (2.1) ist die Karhunen-Loève Entwicklung
die einzige, sodass die stochastischen Fourierkoeffizienten unkorreliert sind, und die
Karhunen-Loève Entwicklung mit aufsteigend geordneten Eigenwerten minimiert den
Quadratmittelfehler.
Bemerkung 2.8. Die Karhunen-Loève ist nur für wenige Prozesse analytisch bekannt, kann
aber numerische durch numerisches Bestimmen der Eigenfunktionen und Eigenwerte der
Kovarianzfunktion gelöest werden. Im diskreten, endlichen Fall, d.h., für (Xt )t∈I = (X1 , . . . , Xn ),
entspricht die Karhunen-Loève Zerlegung der Hauptkomponentenanalyse in der multivariaten Statistik. Im Vergleich zur obigen Zerlegung der Brownschen Bewegung im Satz von
Levy-Ciesielski ist die Karhunen-Loève Entwicklung bi-orthogonal, da sowohl Zn orthogonal im Raum der quadrat-integrierbaren Zufallsvariablen als auch ϕn in L2 (0, 1) orthogonal
sind. Ist zusätzlich zu den Bedingungen in Satz 2.8 der Prozess X ein Gaussprozess, dann
sind die stochastischen Fourierkoeffizienten Zn unabängig normalverteilt.
Beweis von Satz 2.8. Es gilt die Kovarianzfunktion eines Prozesses X, der die Bedingungen
des Satzes 2.8 erfüllt, ist per definitionem ein Mercer-Kern. Somit ist (i) erfüllt und wir
können den Prozess als Fourierreihe bezüglich der ONB aus Eigenfunktionen schreiben,
Dies ist keine Einschränkung da wir aus jedem Prozess mittels Xt − EXt einen zentrierten Prozess
erhalten.
1
2.4. REIHENENTWICKLUNG DER BROWNSCHEN BEWEGUNG
35
wobei die Konvergenz vorerst f.s. in L2 (0, 1) gilt. Für die stochastischen Fourierkoeffizienten
gilt wegen des Satzes von Fubini
Z
1
EZn =
EXt ϕn (t) dt = 0
0
und
EZn Zm
hZ
= E
0
1
Z
0
1
Z 1Z 1
i
Xt Xs ϕn (t)ϕm (s) dt ds =
E[Xt Xs ]ϕn (t)ϕm (s) dt ds
0
0
Z 1Z 1
=
KX (s, t)ϕn (t)ϕm (s) dt ds
0
0
Z 1 Z 1
=
KX (s, t)ϕn (t) dt ϕm (s) ds
Z0 1 0
=
λn ϕn (s)ϕm (s) ds
0
= δnm λn .
Somit haben wir auch (ii) gezeigt. Aus diesen Gleichungen folgt auch sofort die Umkehrung
dieser Aussage in (iv). Wir sehen, dass für Zm unkorreliert zu allen Zn , n 6= m, gelten muss,
dass TKX ϕm orthogonal zu allen ϕn , n 6= m, ist. Daher liegt TKX ϕm im Orthognalraum zu
(ϕn )n6=m . Dieser ist aber durch {ϕm } aufgespannt und somit ist ϕm eine Eigenfunktion zu
TKX . Diese Überlegung gilt für alle m ∈ N und daher besteht eine ONB die unkorrelierte
Fourierkoeffizienten liefert aus Eigenfunktionen zu TKX .
Wir zeigen als nächstes (iii) die gleichmässige Konvergenz im Quadratmittel:
n
n
n
2
X
2
X
X
2
EXt −
Zn ϕn (t) = EXt + E
Zn ϕn (t) − 2EXt
Zn ϕn (t)
k=1
k=1
= KX (t, t) + E
= KX (t, t) +
= KX (t, t) −
k=1
n
X
Zk Zm ϕk (t)ϕk (t) − E
k,m=1
n
X
n
X
k=1
k=1
λk ϕ2k (t) − 2
n
X
n Z
X
k=1
1
Xt Xs ϕk (s)ϕk (t) ds
0
λk ϕ2k (t)
λk ϕ2k (t) .
k=1
Da der letzte Term laut dem Satz von Mercer gleichmässig gegen null konvergiert folgt
(iii). Es bleibt zu zeigen, dass die Karhunen-Loève Entwicklung den Quadratmittelfehler minimiert. Sei ϕ
bn , n ∈ N, eine beliebige ONB in L2 (0, 1) und Zbn die dazugehörigen
36
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
stochastischen Fourierkoeffizienten. Dann erhalten wir den Quadratmittelfehler
∞
n
2
i
h X
X
b
b
b
b
Zk Z m ϕ
bk (t)ϕ
bm (t)
Zn ϕ
bn (t) = E
EXt −
k=1
=
k,m=n+1
∞
Z 1
X
k,m=n+1
Z
0
1
KX (s, r)ϕ
bk (r)ϕ
bm (s) ds dr ϕ
bk (t)ϕ
bm (t) .
0
Durch die Orthogonalität der Basisfunktionen erhalten wir weiters
Z 1 n
∞ Z 1Z 1
2
X
X
b
n 2
b
b
b
KX (s, t)ϕ
bk (t)ϕ
bk (s) ds dt .
EXt −
Zn ϕ
bn (t) dt =
EkX − X kL2 =
0
k=1
k=n+1
0
0
Wir minimieren diesen Term unter der Nebenbedingung der Normierung der Basisfunktionen mittels der Methode der Lagrange-Multiplikatoren und erhalten
∞ Z 1 Z 1
Z 1
X
F (ϕ
bn+1 , ϕ
bn+2 . . .) =
KX (s, t)ϕ
bk (t)ϕ
bk (s) ds dt − βk
ϕ
b2k (t) dt − 1
=
k=n+1
∞
X
0
0
0
TKX ϕ
bk , ϕ
bk
L2
− βk (ϕ
bk , ϕ
bk )L2 − 1 .
k=n+1
(Frèchet-)Ableiten liefert für jedes k ≥ n + 1
∂F
= 2 TKX ϕ
bk , · L2 − 2βk ϕ
bk , · L2 ∈ L(L2 (0, 1), R) = (L2 (0, 1))∗ , L2 (0, 1)
∂ϕ
bk
Nullsetzen der Frèchet-Ableitungen liefert die Gleichungen
TKX ϕ
bk = βk ϕ
bk
in L2 (0, 1)
∀ k ≥ n + 1.
Diese sind genau dann erfüllt falls ϕ
bk eine Eigenfunktion zu TKX mit Eigenwert βk ist.
Beispiel 2.7 (Brownsche Bewegung). Eine Brownschen Bewegung B hat Kovarianzfunktion
K(t, s) = t∧s. Diese ist ein Mercer-Kern und man erhält die orthogonalen Eigenfunktionen
mit dazugehörigen Eigenwerten
√
1
ϕn (t) = 2 sin n − 12 π t , λn =
2 , n ∈ N .
n − 12 π 2
Daher ist die Karhunen-Loève Entwicklung
1
∞
sin
n
−
πt
√ X
2
Bt = 2
Zn
2
n − 21 π 2
n=1
mit Zn u.i.v. N (0, 1).
∀ t ∈ [0, 1]
2.4. REIHENENTWICKLUNG DER BROWNSCHEN BEWEGUNG
37
Beispiel 2.8 (Brownsche Brücke). Eine Brownschen Brücke X hat Kovarianzfunktion K(t, s) =
t ∧ s − ts. Diese ist ein Mercer-Kern und man erhält die orthogonalen Eigenfunktionen mit
dazugehörigen Eigenwerten
ϕn (t) =
√
2 sin n π t ,
λn =
1
,
n2 π 2
n ∈ N.
Daher ist die Karhunen-Loève Entwicklung
∞
√ X
sin n π t
Xt = 2
Zn
nπ
n=1
mit Zn u.i.v. N (0, 1).
∀ t ∈ [0, 1]
38
KAPITEL 2. DIE BROWNSCHE BEWEGUNG
Kapitel 3
Martingale
Wir führen den Martingalbegriff und verwandte Definitionen ein. Wir zeigen,
dass jedes Submartingal unter den üblichen Bedingungen und die Filtration eine f. s. càdlàg Modifikation besitzt. Aus den dazu benötigen Hilfsresultaten ergeben sich allgemeine Lp -Maximalungleichungen, Martingalkonvergenzsätze und
das Optional Stopping Theorem. Wir behandeln ausführlich die quadratische Variation von Martingale und die Doob-Meyer Zerlegung. Zuletzt wird noch kurz die
schwache Konvergenz von Martingalen und das Konzept des Martingalproblems
erläutert.
In diesem Abschnitt behandeln wir grundlegende Eigenschaften von Martingalen in stetiger
Zeit, d.h., I = R+ = [0, ∞). Weiters ist in diesem Kapitel der Zustandsraum aller Prozesse
immer durch die reellen Zahlen und der dazugeörigen Borel-σ-Algebra, d.h., durch (E, E) =
(R, B(−∞, ∞)), gegeben. Wenn nicht speziell darauf hingewiesen, ist im Folgenden immer
ein fixer filtrierter Wahrscheinlichkeitsraum (Ω, F, (Ft )t≥0 , P) angenommen. Somit sind die
folgenden Definition eines Martingals immer bezüglich einer bestimmten Filtration, die
keinen (!) Beschränkungen , z.B., Vollständigkeit oder Rechts-stetigkeit, unterlegen ist.
Definition 3.1. Ein adaptierter, reeller, stochastischer Prozess X heißt Martingal falls
E|Xt | < ∞ für alle t ≥ 0 und
E Xt |Fs = Xs f.s.
∀s ≤ t.
(3.1)
Bemerkung 3.1. Die meisten Eigenschaften von Martingalen, die wir im Folgenden besprechen, bleiben erhalten wenn man in der Definition die Integrierbarkeit der Zufallsvariablen
durch die schwächere Bedingung der Integrierbarkeit des Positivteils, d.h., durch die Bedingung EXt+ < ∞ für alle t ≥ 0, ersetzt, vgl. [RY99]. In diesem Fall spricht man von einem
Martingal nach Definition 3.1 als ein integrierbares Martingal. Im Falle von rechts-stetigen
Martingalen sind beide Begriffe äquivalent, s. Bemerkung 3.2.
Klarerweise bleibt die Martingaleigenschaft erhalten wenn die Filtration durch eine gröbere
Filtration ersetzt wird aber es gibt keinen Grund warum das auch bei Ersetzung durch eine
feinere Filtration auch gelten sollte. Ausnahmen sind hier natürlich die Vervollständigung
und Augmentierung einer Filtration, welche die Martingaleigenschaft erhält.
39
40
KAPITEL 3. MARTINGALE
Beispiel 3.1 (Brownsche Bewegung). Ist B eine Brownsche Bewegung bezüglich (Ft )t≥0
dann ist B ein f.s. stetiges Martingal. Aus der Eigenschaft der unabhängig normalverteilten
Zuwächse folgt E|Bt | = (2t/π)1/2 < ∞ und
E[Bt |Fs ] = E[Bs + (Bt − Bs )|Fs ] = Bs + 0 .
Weiters sind auch die Prozesse Bt2 −t und die geometrische Brownsche Bewegung exp(σBt −
σ 2 t/2), σ ∈ R, Martingale. Im ersten Fall gilt E|Bt2 − t| ≤ 2t und die Unabhn̈gigkeit der
Inkremente gibt
E[Bt2 − t|Fs ] = Bs2 + 2 Bs E[Bt − Bs |Fs ] + E[(Bt − Bs )2 |Fs ] − t = Bs2 + 0 + (t − s) − t .
Im zweiten Fall verwenden wir die Momenterzeugende Funktion der Normalverteilung,
daher
2
2
2
2
E eσBt −σ t/2 = e−σ t/2 E eσBt = e−σ t/2 eσ t/2 = 1 < ∞
und
2
2
2
2
2
E eσBt −α t/2 Fs = eσBs −σ t/2 E eσ(Bt −Bs ) = eσBs −σ t/2 eσ (t−s)/2 = eσBs −σ s/2 .
Beispiel 3.2 (Kompensierter Poisson Prozess). Sei N = (Nt )t≥0 ein Poisson Prozess mit
e = (N
et )t≥0 definiert durch
Intensität λ > 0, dann ist der kompensierte Poisson Prozess N
et := Nt − λt
N
ein f.s. rechts-stetiges Martingal. Die Integrierbarkeit folgt aus der Integrierbarkeit des
Poisson-Prozesses da E|Nt − λt| ≤ E|Nt | + λt = 2λt < ∞ und die Martingaleigenschaft
folgt aus der Bedingung der unabhängigen poissonverteilten Zuwächsen:
et |Fs ] = E[Ns + (Nt − Ns )|Fs ] − λt = Ns + λ(t − s) − λt = N
es .
E[N
Die f.s. Rechts-stetigkeit folgt sofort aus der f.s. Rechts-stetigkeit des Poisson-Prozesses.
Beispiel 3.3. Sei Y eine integrierbare Zufallsvariable und (Ft )t≥0 eine Filtration dann erhalten wir ein Martingal X, wenn wir jeweils Xt = E[Y |Ft ] setzen. Die Integrierbarkeit
folgt aus der Jensen’schen Ungleichung und die Martingaleigenschaft aus der Projektionseigenschaft des bedingten Erwartungswertes.
Definition 3.2. Wird in der Definition 3.1 die Eigenschaft (3.1) durch
∀s ≤ t.
E Xt |Fs ≤ Xs f.s.
(3.2)
ersetzt, dann heißt der Prozess X ein Supermartingal, wird (3.1) durch
E Xt |Fs ≥ Xs f.s.
∀s ≤ t.
(3.3)
ersetzt, dann heißt der Prozess X ein Submartingal.
41
Trivialerweise gilt, dass ein Martingal sowohl ein Super- als auch ein Submartingal ist,
weiters ist X ein Supermartingal so ist −X ein Submartingal und X ist ein Martingal
falls sowohl X und −X ein Supermartingal sind. Durch diese Transformationen kann jede
bewiesene Eigenschaft eines Sub-/Supermartingals einfach in eine Eigenschaft des anderen
übertragen werden und gilt klarerweise auch für Martingale. Offenbar gilt, dass t 7→ EXt für
ein Martingal konstant, ein Supermartingal monoton fallend und Submartingal monoton
wachsend ist.
Beispiel 3.4 (Geometrische Brownsche Bewegung). Wir haben in Beispiel 3.1 bereits gezeigt, dass die geometrischen Brownsche Bewegung Xt = exp σBt + (µ − σ 2 /2)t für µ = 0
ein Martingal ist. Daraus sieht man sofort, dass die geometrische Brownsche Bewegung für
µ > 0 ein Submartingal und für µ < 0 ein Supermartingal ist.
Beispiel 3.5 (Poisson Prozess). Der Poisson Prozess N ist ein Submartingal da E|Nt | =
λt < ∞ und
E[Nt |Fs ] = Ns + E[Nt − Ns |Fs ] = Ns + λ(t − s) ≥ Ns .
Aus (Sub-/Super-)Martingalen erhält man durch einfache Transformationen wiederum
(Sub-/Super-)Martingale. Sind X, Y Martingale, dann ist auch aX + bY ein Martingal
für alle a, b ∈ R. Sind X, Y Supermartingale dann ist min{Xt , Yt } ein Supermartingal und
für alle a, b > 0 ist auch aX + bY ein Supermartingal. Sind X, Y Submartingale dann ist
max{Xt , Yt } ein Submartingal.
Beispiel 3.6 (Geburts-Todes-Prozess). Ein unreflektierter Geburts-Todes-Prozess Z kann
als die Differenz zweier unabhängiger Poisson-Prozesse N λ , N µ mit Geburtsrate λ und
Todesrate µ geschrieben werden, d.h., Zt = Ntλ − Ntµ , und somit gilt Zt − t(µ − λ) ist ein
Martingal.
Weitere Transformationen, die die Submartingal-Eigenschaft erhalten, ergeben sich aus der
Jensen’schen Ungleichung.
Proposition 3.1. (i) Sei X ein Martingal und ϕ eine konvexe Funktion, sodass für alle
t ≥ 0 gilt E|ϕ(Xt )| < ∞, dann ist ϕ(X) ein Submartingal.
(ii) Sei X ein Submartingal und ϕ zusätzlich zu den obigen Eigenschaften nicht-fallend,
dann ist ϕ(X) ein Submartingal.
Beweis. Die Jensen’sche Ungleichung gibt für s, t ≥ 0, dass
ϕ(Xt ) ≤ ϕ(E[Xt+s |Ft ]) ≤ E[ϕ(Xt+s )|Ft ] ,
wobei im Fall (i) die erste Ungleichung sogar eine Gleichung ist und im Fall (ii) gilt, da ϕ
nicht fallend ist.
Beispiel 3.7. Sei X ein Martingal dann sind (Xt − c)+ und (Xt − c)− Submartingale für
alle c ∈ R. Ist X für p ≥ 1 ein p-fach integrierbares Martingal oder positives Submartingal
dann ist |Xt |p ein Submartingal.
42
KAPITEL 3. MARTINGALE
Im den folgenden drei Abschnitten dieses Kapitel werden wir einige nützliche technische
Resultate für Submartingale beweisen, die wir vor allem dazu verwenden um die beiden
folgenden Aspekte zu behandeln.
1.
Stetigkeit der Pfade: Eine wünschenswerte Eigenschaft von stochastischen Prozessen ist, dass sie rechts-stetige Pfade besitzen. Dies gilt vor allem für viele Resultate von
(Sub-)Martingalen. Daher ist es eine Frage von Interesse ob Martingale gute Pfadeigenschaften haben. Mit Beispiel 3.3 haben wir eine einfache Methode um ein Martingal
zu konstruieren. Für dieses stellt sich natürlich die Frage welche Eigenschaften die Pfade eines derartigen Martingals oder einer Modifikation haben, die a-priori natürlich
nicht notwendigerweise gut sein müssen.
2.
Langzeitverhalten von Martingalen: Ein Prozess besitzt eine terminale Zufallsvariable X∞ falls Xt → X∞ f.s. für t → ∞. Die Frage ist wann gibt es terminale
Zufallsvariablen für Martingale und, z.B., im Falle von Martingalen wie in Beispiel
3.3 definiert, gilt X∞ = Y . Im Zusammenhang mit der ersten Frage ergibt sich: Kann
jedes Martingal auf diese Weise erzeugt werden?
3.1
Martingalungleichungen
Die folgenden Ungleichungen sind klassische Resultate der Martingaltheorie und gehen
meist auf J. L. Doob zurück. Wir präsentieren die Ungleichungen in Satz 3.1 und 3.2
über den Intervallen [0, T ]. Natürlich gelten die Ungleichungen für jedes beliebige endliche
Intervall und lassen sich, wann immer sinnvoll definiert, mittels T → ∞ auf ganz R+
ausdehnen. Zuerst behandeln wir aber eine erste, diskrete Version des Optimal Stopping
Theorems, welches im Kapitel 3.4 unter zusätzlichen Bedingungen verallgemeinert wird.
Lemma 3.1. Seien τ1 , τ2 beschränkte Stoppzeiten, die nur endlich viele Werte annehmen,
dann gilt für ein Submartingal X, dass
E Xτ1 Fτ2 ≥ Xτ1 ∧τ2 f.s.
(3.1)
Ist X ein Martingal, dann gilt in (3.1) sogar Gleichheit.
Beweis. Wir beweisen den Satz für Submartingale und im Falle von Martingalen werden
alle Ungleichungen zu Gleichungen. Es sind t1 < t2 < . . . tm jene Werte in R+ , welche die
Stoppzeiten annehmen, und wir müssen zeigen, dass
Z
Z
Xτ1 dP ≥
Xτ1 ∧τ2 dP
∀ A ∈ Fτ2 .
(∗)
A
Da aber A =
Sm
i=1
Z
A
A ∩ [τ2 = ti ] reicht es für alle i = 1, . . . , m
Z
Z
Xτ1 dP ≥
Xτ1 ∧τ2 dP =
A∩[τ2 =ti ]
A∩[τ2 =ti ]
A∩[τ2 =ti ]
Xτ1 ∧τi dP
3.1. MARTINGALUNGLEICHUNGEN
43
zu zeigen. Da aber aus Definition der gestoppten σ-Algebra A ∩ [τ2 = ti ] ∈ Fti folgt, gilt,
dass (∗) auf jedem Fall dann erfüllt ist, falls für alle i = 1, . . . , m gilt
E[Xτ1 |Fti ] ≥ Xτ1 ∧ti .
(∗∗)
Nun gilt aber weiters
E[Xτ1 ∧tk+1 |Ftk ] = E[Xtk+1 I[τ1 >tk ] + Xτ1 ∧tk+1 I[τ1 ≤tk ] |Ftk ]
= E[Xtk+1 |Ftk ] I[τ1 >tk ] + Xτ1 ∧tk+1 I[τ1 ≤tk ]
≥ Xtk I[τ1 >tk ] + Xτ1 ∧tk+1 I[τ1 ≤tk ]
= Xτ1 ∧tk .
Verwendet man diese Abschätzung iterativ startend mit k = m − 1, folgt (∗∗).
Nun folgen die ersten Ungleichungen für Submartingale. Die Ungleichungen gelten auch im
diskreten Fall, d.h., das Supremum wird über eine höchstens abzählbare Menge genommen.
In diesem Fall kann die Annahme der Rechts-stetigkeit fallengelassen werden.
Satz 3.1 (Doobsche Lp -Ungleichung). Sei X ein rechts-stetiges Martingal oder positives
Submartingal, dann gilt für p ≥ 1
h
i
1
P supt∈[0,T ] |Xt | ≥ ≤ p supt∈[0,T ] E|Xt |p
(3.2)
und für p > 1
E supt∈[0,T ] |Xt |p
1/p
≤
1/p
p
supt∈[0,T ] E|Xt |p
p−1
(3.3)
Wir bemerken and dieser Stelle, dass für p > 1 jedes p-fach integrierbare Submartingal,
was impliziert, dass die rechten Seiten der Ungleichungen in Satz 3.1 endlich sind, nach
Satz A.2 über endlichen Intervallen gleichgradig integrierbar ist.
Beweis. Wir nehmen im Folgenden an, dass X auf [0, T ] p-fach integrierbar ist, ansonsten
sind die Ungleichungen trivialerweise erfüllt. Seien t1 < t2 < . . . < tm beliebige endlich
viele Zeitpunkte in [0, T ]. Dann definiert
(
τ :=
inf{ti : Xti ≥ } falls ein derartiges i existiert,
tm
sonst
eine Stoppzeit, die nur endlich viele Werte annimmt. Der Prozess X sei vorerst ein beliebiges
Submartingal. Da τ ≤ tm f.s. folgt mittels Lemma 3.1
EXtm ≥ EXτ = E Xτ I[supi Xti ≥] + E Xτ I[supi Xti <]
≥ P supi Xti ≥ + E Xtm I[supi Xti <] .
44
KAPITEL 3. MARTINGALE
Wir ziehen den letzten Term auf beiden Seiten ab und erhalten
P supi Xti ≥ ≤ E Xtm I[supi Xti ≥] ≤ E|Xtm | .
(∗)
Wir zeigen nach diesen Vorbemerkungen nun die Doobschen Ungleichungen zuerst für
endliche Suprema und erweitern die Aussagen dann auf Suprema über dem Intervalle [0, T ].
(i) Sei nun X ein Martingal oder positives Submartingal, dann ist |X|p wegen Proposition
3.1, vgl. Bsp. 3.7, ein Submartingal und aus (∗) folgt
1
1 P supi |Xti | ≥ ≤ p E |Xtm |p ] = p supi E |Xti |p ] ,
wobei wir für die Gleichung verwendet haben, dass die Mittelwertfunktion für ein Submartingal monoton wachsend ist. Somit ist die endliche Version von (3.2) bewiesen.
Um die zweite Ungleichung (3.3) zu beweisen, definieren wir X ∗ := supi |Xti | und erhalten
aus (∗) für alle n ∈ N
hZ X ∗ ∧n
i
hZ n
i
∗
p
p−1
p−1
E[(X ∧ n) ] = E
p s ds = E
p s I[X ∗ ≥s] ds
0
Z n0
=
p sp−1 P X ∗ ≥ s ds
Z0 n
≤
p sp−2 E |Xtm | I[X ∗ ≥s] ds
0
Z X ∗ ∧n
h
i
p−2
= p E |Xtm |
s ds
0
p
E |Xtm | (X ∗ ∧ n)p−1 .
=
p−1
Als nächstes wenden wir die Hölder-Ungleichung auf die rechte Seite an und erhalten
E[(X ∗ ∧ n)p ] ≤
1/p
(p−1)/p
p
E|Xtm |p
E(X ∗ ∧ n)p
.
p−1
und nach Division der entsprechenden Terms
1/p
E[(X ∗ ∧ n)p ]
≤
1/p
1/p
p
p
≤
.
E|Xtm |p
supi E|Xtm |p
p−1
p−1
Wir betrachten den Limes für n → ∞ und erhalten wegen dem Satz von der Monotonen
Konvergenz die endliche Version der Lp -Ungleichung (3.3).
(ii) Der Beweis endet mit der Erweiterung der Resultate auf Intervalle. Da X ein rechtsstetiger Prozess ist, reicht es die Suprema auf einer dichten abzählbaren Menge D ⊂ [0, T ]
zu betrachten.
Weiters gibt es dann eine wachsende Folge von endlichen Mengen Dn sodass
S
D = n∈N Dn und wir können die obigen Ergebnisse auf die Indexmengen Dn anwenden.
3.1. MARTINGALUNGLEICHUNGEN
45
Die Ungleichung im Satz folgen nun im Limes von n → ∞ wegen der Monotonie der
Erwartungswertfunktion für Submartingale und einerseits wegen der Stetigkeit von unten
von Wahrscheinlichkeitsmaßen da
supDn Xt |p ≥ λ] ↑ supD Xt |p ≥ λ] = sup[0,T ] Xt |p ≥ λ]
und da
lim E supDn |Xt |p = E supD |Xt |p
n→∞
laut dem Satz von der Monotoner Konvergenz.
Grundlegend um die pfadweise Regularität von Submartingalen X zu untersuchen, s. den
folgenden Abschnitt, sind Abschätzungen der Anzahl der erwarteten Kreuzungen der Pfade
eines Submartingals X über ein Interval [a, b], die wir in einem separatem Lemma vorwegnehmen wollen. Sei F eine endliche Teilmenge von [0, ∞) und für jedes Intervall (a, b)
definieren wir rekursiv
τ1 := min{t ∈ F : Xt ≤ a}
(3.4)
für k ≥ 1
und für k ≥ 1
σk := min{t > τk : t ∈ F, Xt ≥ a}
(3.5)
τk+1 := min{t > σk : t ∈ F, Xt ≥ a} .
(3.6)
Die Zufallsvariable U (X, F, (a, b)) := max{k : σk < ∞} bezeichnet die Anzahl der Überkreuzungen des Intervalls (a, b) nach oben beschränkt auf die Zeiten in F . Analog bekommen wir die Definition der Kreuzungen nach unten. Für beliebige Teilmengen F von
R+ definieren wird die Anzahl der Kreuzungen als das Supremum über die Anzahl der
Kreuzungen aller endlichen Teilmengen von F . Diese Suprema sind Zufallsvariablen falls
entweder F abzählbar oder das Submartingal X zusätzlich rechts-stetig ist. Schlußendlich
verwenden wir für Intervalle die Notation
D(X, T, (a, b)) := sup D(X, F, (a, b)) ; F ⊂ [0, T ], F endlich ,
U (X, T, (a, b)) := sup U (X, F, (a, b)) ; F ⊂ [0, T ], F endlich .
Dann gelten folgenden Abschätzungen, wobei man für diskrete Indexmengen an Stelle des
Intervalls [0, T ] die Bedingung der rechts-stetigen Pfade fallen lassen kann.
Lemma 3.2 (Kreuzungsungleichungen). Sei X ein rechts-stetiges Submartingal, dann gilt
für jedes Interval (a, b) ⊂ [0, T ], dass die Kreuzungen nach unten
E D(X, T, (a, b)) ≤
1
supt∈[0,T ] E(Xt − b)+
b−a
(3.7)
erfüllen und die Kreuzungen nach oben erfüllen
E U (X, T, (a, b)) ≤
1
supt∈[0,T ] E(Xt − a)+ .
b−a
(3.8)
46
KAPITEL 3. MARTINGALE
Beweis. Ähnlich wie im Beweis der Lp -Ungleichungen zeigen wir die Resultate zuerst für
endliche und abzählbare Indexmengen und schließen dann mittels der Rechts-stetigkeit der
Pfade auf beschränkte Intervalle. Weiters zeigen wir die Ungleichung nur für die Kreuzungen nach oben, da das Resultat für die Kreuzungen nach unten analog bewiesen wird.
(i) Sei F ⊂ [0, T ] eine endliche Menge, dann folgt aus Satz 3.1, da σk ∧ T ≤ τk+1 ∧ T
(beides endliche Stoppzeiten mit nur endlich vielen Werten), dass
∞ hX
i
0 ≤ E
Xτk+1 ∧T − Xσk ∧T
k=1
hU (X,F,(a,b))
= E
X
Xτk+1 ∧T − Xσk ∧T
i
k=1
h
= E −
U (X,F,(a,b))
X
i
Xσk ∧T − Xτk ∧T − Xσ1 ∧T − a + XτU (X,F,(a,b))+1 ∧T − a
k=2
h
i
≤ E −(b − a) U (X, F, (a, b)) + XτU (X,F,(a,b))+1 ∧T − a
≤ −(b − a) EU (X, F, (a, b)) + E XT − a
+
.
Da nach Satz 3.1 der Prozess (Xt − a)+ ein Submartingal ist und daher E(XT − a)+ =
supt∈[0,T ] E(Xt −a)+ , folgt die Abschätzung (3.8), wobei die linken Seite durch EU (X, F, (a, b))
ersetzt wird.
(ii) Der Übergang von endlichem zu abzählbaren Indexmengen erfolgt mittels des Satzes
von der MonotonenSKonvergenz. Sei Fn ein wachsende Folge von endlichen Teilmengen von
[0, T ], sodass F = n Fn dicht in [0, T ] liegt. Dann gilt
U (X, Fn , (a, b)) ↑ U (X, F, (a, b)) = U (X, T, (a, b)) f.s.
wegen der Rechts-stetigkeit der Pfade und (3.8) folgt aus dem Satz von der Monotonen
Konvergenz.
3.2
Regularitätsatz für Submartingale
Ein Ziel dieses Kapitel ist der folgenden Satz, der erlaubt dass meistens ohne Beschränkung
der Allgemeinheit ein (Sub-/Super-)Martingal als càdlàg vorausgesetzt werden kann und
/ oder der Wahrscheinlichkeitsraum die üblichen Bedingungen erfüllt. Dieses Ergebnis
ergibt sich als Folgerung zum Regularitätssatzes von Submartingalen. Zum Beweis des
Regularitätssatzes benötigt man die Kreuzungsungleichungen im vorherigen Kapitel über
abzählbaren Indexmengen, d.h., wir benötigen keine Annahmen an die Rechts-stetigkeit
der Pfade, die ja gerade das Ziel des Regularitätssatzes ist.
Satz 3.2 (Regularitätssatz). Sei X ein Submartingal. Dann gilt für fast alle ω ∈ Ω, dass
für alle t ∈ (0, ∞) der linksseitige Limes lims↑t,s∈Q Xs (ω) und für alle t ∈ [0, ∞) der
rechtsseitige Limes lims↓t,s∈Q Xs (ω) existiert.
3.3. MARTINGALKONVERGENZSÄTZE
47
Beweis. Es reicht aus die Aussage des Satzes für die Intervalle [0, T ], T > 0, zu zeigen. Es
gilt
E(Xt − b)+ ≤ b− + EXT+ < ∞
∀ t ∈ [0, T ]
und daher gilt wegen der diskreten Version der Kreuzungsungleichungen in Lemma 3.2,
für welche wir die Annahme rechts-stetiger Pfade nicht benötigen, dass ein Ω0 ⊂ Ω mit
P(Ω0 ) = 1 existiert und
D(X(ω), [0, T ] ∩ Q, (a, b)) < ∞
∀ a < b, a, b ∈ Q, ω ∈ Ω0 .
(∗)
Wir zeigen die f.s. Existenz der linken Limiten mit einem Widerspruch zu (∗). Die Existenz
der rechten Limiten folgt mit einem analogen Argument. Sei t ∈ [0, T ], dann gilt, falls der
Grenzwert lims↑t,s∈Q Xs nicht f.s. existiert, dass es zwei rationale Zahlen a, b gibt, so dass
lim inf Xs < a < b < lim sup Xs
s↑t,s∈Q
s↑t,s∈Q
mit positiver Wahrscheinlichkeit. Das heißt aber, dass D(X, [0, T ] ∩ Q, (a, b)) = ∞ mit
positiver Wahrscheinlichkeit. Das aber gibt einen Widerspruch zu (∗).
Konsequenzen des Regularitätssatzes sind, dass o.B.d.A. für rechts-stetige Submartingale angenommen werden kann, dass der zugrundeliegende Wahrscheinlichkeitsraum die
üblichen Bedingungen erfüllt und umgekehrt, dass ein Submartingal auf einem Wahrscheinlichkeitsraum, der die üblichen Bedingungen erfüllt, o.B.d.A. als càdlàg angenommen werde
kann. Insbesondere gilt, dass jedes Martingal, da ja t 7→ EXt konstant ist, eine f.s. càdlàg
Modifikation besitzt. Diese Resultate sind im folgenden Satz zusammengefasst, den wir
hier nicht beweisen werden und verweisen auf die Literatur [EK86, KS91, RY99].
Korollar 3.1. (i) Sei X ein rechts-stetiges (Sub-)Martingal bezüglich einer Filtration
(Ft )t≥0 , dann ist X f.s. càdlàg und X ist ein (Sub-)Martingal bezüglich der Filtration (Ft+ )t≥0 und der Vervollständigung / Augmentierung davon.
(ii) Sei X ein (Sub-)Martingale bezüglich einer rechts-stetigen, vollständigen Filtration
(Ft )t≥0 und die Mittelwertfunktion t 7→ EXt sei rechts-stetig, dann besitzt X eine
càdlàg Modifikation, die ebenfalls ein (Ft )t≥0 -(Sub-)Martingal ist.
3.3
Martingalkonvergenzsätze
Wir betrachten nun das Grenzverhalten von rechts-stetigen Submartingalen für t → ∞.
Anhand der Kreuzungsungleichungen erhält man eine einfache, hinreichende Bedingung
für die Existenz eines f.s. Grenzwertes X∞ . Danach werden wir Folgerungen davon und
auch hinreichend und notwendige Bedingungen betrachten.
Satz 3.3 (Konvergenzsatz für Submartingale). Sei X ein f.s. rechts-stetiges Submartingal.
Gilt supt≥0 EXt+ < ∞, dann konvergiert Xt f.s. gegen eine F∞ -messbare Zufallsvariable
X∞ und E|X∞ | < ∞.
48
KAPITEL 3. MARTINGALE
Beweis. Wegen der Kreuzungsungleichung gilt für alle T > 0
EU (X, T, (a, b)) ≤
E(XT − a)+
EXT+ − |a|
≤
<∞
b−a
b−a
und der Satz von der Monotonen Konvergent impliziert für T → ∞
EU (X, R+ , (a, b)) ≤
supt≥0 EXt+ − |a|
.
b−a
Daraus folgt, dass für alle −∞ < a < bS< ∞ die Mengen [U (X, R+ , (a, b)) = ∞] Nullmengen sind und ebenso die Menge N = a<b, a,b∈Q [U (X, R+ , (a, b)) = ∞] welche die Menge
[lim inf t→∞ Xt < lim supt→∞Xt ] beinhaltet. Daraus folgt limt→∞ Xt (ω) := X∞ (ω) existiert
für alle ω ∈ Ω\N . Weiters ist X∞ messbar als f.s. punktweiser Limes messbarer Funktionen
und die Annahme supt≥0 EXt+ < ∞ impliziert die Beschränktheit von Xt in L1 (P) da
sup E|Xt | ≤ sup 2EXt+ − EXt ≤ 2 sup EXt+ − EX0 .
t≥0
t≥0
t≥0
Aus Fatou’s Lemma – E|X∞ | ≤ limt→∞ E|Xt | – folgt nun die Integrierbarkeit von X∞ .
Bemerkung 3.2. Im Beweis haben wir gesehen, dass für ein rechts-stetiges Submartingal
die Bedingungen supt≥0 EXt+ < ∞ und supt≥0 E|Xt | < ∞ äquivalent sind.
Beispiel 3.8 (Supermartingal-Konvergenz). Jedes positive Supermartingal X konvergiert
fast sicher. Dies folgt sofort aus Satz 3.3 da −X ein negatives Submartingal ist und somit
supt≥0 E(−Xt )+ = 0 < ∞.
Beispiel 3.9 (Geometrische Brownsche Bewegung). Sei Xt = exp(σBt + (µ − σ 2 /2)t) eine
geometrische Brownsche Bewegung, dann ist X für µ ≤ 0 ein positives Supermartingal und
konvergiert somit nach dem vorherigen Beispiel f.s. gegen eine integrierbare Zufallsvariable
X∞ . In diesem Falle gilt X∞ = 0 f.s., vgl. Abb. 2.1, da man sogar zeigen kann, dass Xt → 0
f.s. falls µ − σ 2 /2 < 0. In diesem Fall gilt, dass die Verteilungsfunktion von Xt gegen durch
2 /2)t
√
Φ ln x−(µ−σ
I(0,∞) (x) −→ I[0,∞) (x)
∀ x ∈ R\{0} .
σ t
Die Heaviside-Funktion I[0,∞) ist aber der Verteilungsfunktion von X∞ = 0. Im Falle µ > 0,
bleibt nur noch zu zeigen, dass neben der schwachen Konvergenz auch die fast sichere
Konvergenz gilt. Aus der schwachen Konvergenz gegen eine Konstante folgt, dass jede Folge
Xtn , n ∈ N, eine f.s. konvergente Teilfolge besitzt. Da dies aber für jede Folge von Indices
gilt, kann man daraus schließen das jede Folge f.s. konvergent sein muss. Aus der Stetigkeit
der geometrischen Brownschen Bewegung schließt man auf den stetigen Grenzübergang.
Wir beschließen diesen Abschnitt in dem wir die f.s. Konvergenz noch zur Konvergenz im
Mittel und p-ten Mittel ausdehnen. Dieser Satz beantwortet auch die letzte offene Frage
zu Martingalen, die mittels Xt = E[Y |Ft ] erzeugt sind.
3.3. MARTINGALKONVERGENZSÄTZE
49
Satz 3.4 (Konvergenz im Mittel). Für ein f.s. rechts-stetiges Martingal oder positives
Submartingal sind die folgenden Bedingungen äquivalent.
(i) Die Familie {Xt , t ≥ 0} is gleichgradig integrierbar.
(ii) Xt konvergiert für t → ∞ in L1 (P).
(iii) Xt konvergiert für t → ∞ f.s. gegen eine integrierbare Zufallsvariable X∞ und (Xt )t∈[0,∞]
ist ein (Sub-)Martingal.
Ist X ein Martingal, dann sind die Bedingungen (i) – (iii) weiters äquivalent zu folgender
Bedingung:
(iv) Es existiert eine integrierbare Zufallsvariable Y sodass Xt = E[Y |Ft ] fast sicher.
Falls (iv) gilt, dann gilt auch, dass E[Y |F∞ ] = X∞ fast sicher mit X∞ aus (iii). Dieses ist
auch f.s. gleich dem L1 (P)-Grenzwert in (ii).
Bemerkung 3.3. Ist der Prozess X ein Submartingal aber nicht f.s. positiv, dann gelten
immer noch die Implikationen (i) ⇒ (ii) ⇒ (iii).
Bemerkung 3.4. Dieser Konvergenzsatz impliziert auch ein Konvergenzresultat für bedingte
Erwartungen bekannt unter dem Namen Lèvys 0-1-Gesetz. Sei Y integrierbar und (Ft )t≥0
eine rechts-stetige, vollständige Filtration, dann gilt
E[Y |Ft ] → E[Y |F∞ ]
f.s. und in L1 (P) .
Der Name resultiert aus der Anwendung, dass für A ∈ F∞ gilt P[A|Ft ] → IA ∈ {0, 1} fast
sicher. Heuristisch ausgedrückt heißt dies nichts anderes, dass wenn wir schrittweise alle
Informationen erhalten, die den Ausgang eines Ereignisses bestimmen, dann werden wir
schrittweise immer sicherer, ob das Ereignis eintritt oder nicht.
Beispiel 3.10 (Geometrische Brownsche Bewegung). Die geometrische Brownsche Bewegung Xt = exp(σBt − σ 2 t/2) ist ein Martingal und X∞ = 0 fast sicher. Es gilt aber
EXt = e0 = 1 und da EX∞ = 0, gilt dass die L1 (P)-Konvergenz sicherlich nicht erfüllt ist.
Um keinen Widerspruch zu Satz 3.4 zu erhalten folgt, das Martingal ist nicht gleichgradig
integrierbar.
Beweis. (i) ⇒ (ii): Da der Prozess X gleichgradig integrierbar ist, folgt die Beschränktheit
in L1 (P) (Satz A.2) und somit nach Satz 3.3 die Existenz eines f.s. integrierbaren Grenzwertes X∞ . Da Konvergenz in L1 (P) äquivalent zur Konvergenz in Wahrscheinlichkeit
(impliziert durch f.s. Konvergenz) und gleichgradige Integrierbarkeit ist, folgt (ii).
(ii) ⇒ (iii): Aus der Konvergenz in L1 (P) folgt die Beschränktheit in L1 (P) und somit nach Satz 3.3 die Existenz eines f.s. integrierbaren Grenzwertes X∞ . Weiters ist die
bedingte Erwartung ein stetiger Operator bezüglich L1 (P) und daher folgt die Submartingaleigenschaft aus Xt ≤ E[Xt+h |Ft ] und dem Grenzübergang h → ∞.
50
KAPITEL 3. MARTINGALE
(iii) ⇒ (i): Um die gleichgradige Integrierbarkeit der Familie {Xt , t ≥ 0} zu erhalten,
reicht es die gleichgradige Integrierbarkeit der Familie {E[X∞ |Ft ], t ≥ 0} zu zeigen, da
|Xt | ≤ |E[X∞ |Ft ]| für alle t ≥ 0. Wir setzen Nt := [|E[X∞ |Ft ]| > n] ∈ Ft und
Z
At :=
|E[X∞ |Ft ]| dP .
Nt
D.h. es bleibt zu zeigen, dass limn→∞ supt≥0 At = 0, vgl. die Definition A.1 der gleichgradigen Integrierbarkeit. Die bedingte Version der Jensen’schen Ungleichung liefert
Z
Z
At ≤
E[|X∞ ||Ft ]dP =
|X∞ | dP
Nt
Nt
und aus der Markov-Ungleichung folgt
E[|E[X∞ |Ft ]|]
E|X∞ |
≤
.
n
n
Daraus folgt aber, dass, wenn nur n groß genug gewählt wird, At unabhängig von t beliebig
klein wird.
P[Nt ] ≤
(iii) ⇒ (iv): Setze Y := X∞ .
(iv) ⇒ (i): Es gilt Xt = E[Y |Ft ] fast sicher und Y ist integrierbar. Da somit Y auch
gleichgradig integrierbar ist, existiert nach Satz A.2 eine nicht-negative, nicht-fallende,
konvexe Funktion G auf R+ , sodass limt→∞ G(t)/t = ∞ und EG(|Y |) < ∞. Wir verwenden
nun zweimal die Jensen’sche Ungleichung und erhalten
sup EG(|Xt |) = sup EG(|E[Y |Ft ]|) ≤ sup EG(E[|Y | |Ft ])
t≥0
t≥0
t≥0
≤ sup E E[G(|Y |)|Ft ]
t≥0
= EG(|Y |) < ∞ .
Daher folgt nach Satz A.2, dass die Familie {Xt , t ≥ 0} gleichgradig integrierbar ist.
Schlussendlich zeigen wir noch den Zusatz zu (iv). Da (iv) ⇒ (i) ⇒ (ii) & (iii) existiert
eine integrierbare, F∞ -messbare Zufallsvariable X∞ , sodass E[Y |Ft ] → X∞ fast sicher und
in L1 (P). Dann gilt für alle A ∈ Ft bei beliebigem t ≥ 0, dass
Z
Z
Z
Z
Y dP =
E[Y |Ft ] dP =
E[X∞ |Ft ] dP =
X∞ dP .
(∗)
S
A
A
A
A
Da aber t≥0 Ft ein Erzeuger von F∞ ist und die Mengen aus F, die (∗) erfüllen eine
monotone Klasse bilden, folgt mittels dem Monoton Class Theorem1 , dass EY IA = EX∞ IA
für alle A ∈ F∞ gilt. Daher ist X∞ eine Version der bedingten Erwartung E[Y |F∞ ].
Schlussendlich, dass im Falle (ii) und (iii) die Konvergenz E|Xt − X∞ | → 0 gilt, folgt
aus der Äquivalenz von Konvergenz im Mittel zur Konvergenz in Wahrscheinlichkeit von
gleichgradig integrierbaren Zufallsvariablen.
1
Sei A eine Algebra und M eine monotone Klasse über Ω. Dann gilt σ(A) ⊂ M.
3.4. OPTIONAL STOPPING THEOREM
51
Zuletzt erweitern wir noch das Konvergenzresultat für beschränkte Submartingale zur Konvergenz in Lp (P).
Satz 3.5 (Lp -Konvergenzsatz). Sei p > 1 und X ein f.s. rechts-stetiges Martingal oder positives Submartingal beschränkt in Lp (P), d.h., supt≥0 E|Xt |p < ∞. Dann ist das Submartingal |X|p gleichgradig integrierbar und es existiert eine p-fach integrierbare, F∞ -messbare
Zufallsvariable X∞ , sodass Xt → X∞ f.s. und in Lp (P).
Beweis. Aus der Lp -Beschränktheit folgt, dass X gleichgradig integrierbar ist und der
f.s. Grenzwert X∞ existiert. Aus der Doobschen Lp -Ungleichung folgt
p p
E supt≥0 |Xt |p ≤
supt≥0 E|Xt |p < ∞ .
p−1
Da somit supt≥0 |Xt |p eine integrierbare Majorante ist, folgt |X|p ist ein gleichgradig integrierbares Submartingal und es existiert ein f.s. integrierbarer Limes. Klarerweise gilt
|Xt |p → |X∞ |p f.s., also stimmt dieser mit dem Limes überein und es folgt E|X∞ |p < ∞.
Der Satz von der Dominierten Konvergenz mit Majorante |Xt − X∞ |p ≤ 2p supt≥0 |Xt |p
liefert nun die Konvergenz in Lp (P).
3.4
Optional Stopping Theorem
Als letztes Resultat erweitern wir Lemma 3.1 zu beliebigen Stoppzeiten. Insbesondere erhalten wir damit auch, dass die (Sub-)Martingaleigenschaft auch für zufällige Zeiten gilt.
Satz 3.6 (Optional Stopping Theorem). Sei X ein f.s. rechts-stetiges Submartingal und
τ1 , τ2 sind zwei beliebige Stoppzeiten.
(i) Ist τ1 is f.s. beschränkt, dann gilt fast sicher
E[Xτ1 |Fτ2 ] ≥ Xτ1 ∧τ2 .
(3.1)
(ii) Ist τ1 f.s. endlich, E|Xτ1 | < ∞ und limt→∞ E|Xt |I[τ1 >t] = 0, dann gilt fast sicher
E[Xτ1 |Fτ2 ] ≥ Xτ1 ∧τ2 .
(3.2)
(iii) Ist X gleichgradig integrierbar, dann gilt fast sicher
E[Xτ1 |Fτ2 ] ≥ Xτ1 ∧τ2 .
(3.3)
Falls X ein Martingal ist, dann gilt in (3.1) – (3.3) sogar Gleichheit.
Bemerkung 3.5. Im Falle τ2 f.s. endlich gilt (iii) ⇒ (ii): Klarerweise gilt |Xt |I[τ1 >t] ≤ |Xt |
und, da letztere gleichgradig integrierbar sind, sind auch |Xt |I[τ1 >t] gleichgradig integrierbar. Weiters konvergieren diese wegen der Endlichkeit der Stoppzeit f.s. gegen 0. Da die
gleichgradige Integrierbarkeit das Vertauschen von Limes und Erwartungswert erlaubt folgt
nun limt→∞ E|Xt |I[τ1 >t] = 0.
52
KAPITEL 3. MARTINGALE
Bemerkung 3.6. Im Falle unbeschränkter Stoppzeiten ist die gleichgradige Integrierbarkeit
in (iii) eine notwendige Bedingung. Wir illustrieren das an Hand eines Beispiels. Für das
nicht gleichgradig integrierbare Martingal Xt = exp(Bt − t/2), s. Bsp. 3.10, sei für ein
c < 1 die Stoppzeit τc := inf{t > 0 : Xt ≤ c} definiert. Dann gilt τc ist unbeschränkt aber
f.s. endlich, da Xt → 0 f.s., und Xτc = c fast sicher. Somit gilt EXτc = c. Andererseits, falls
das Optional Stopping Theorem gelten sollte, dann hätten wir EXτc = EX0 = 1. In Bezug
auf (ii) bedeutet dies, da E|Xτc | = c < ∞, dass EXn I[τc >n] nicht gegen null konvergiert.
Beweis von Satz 3.6. Wir führen den Beweis für Submartingale und es ist klar, dass im
Falle eines Martingals alle Ungleichungen zu Gleichungen werden. Das immer wiederkehrende Argument im folgenden Beweis ist die Konvergenz von Erwartungswerten, die aus der
f.s. Konvergenz und der gleichgradigen Integrierbarkeit der Argumente im Erwartungswert
folgt.
(i) Wir nehmen vorerst an, dass beide Stoppzeiten τ1 , τ2 durch T beschränkt sind, d.h.,
τ1 , τ2 < T fast sicher. Diese Stoppzeiten können dann mittels Folgen von Stoppzeiten, die
nur endlich viele Werten annehmen, punktweise von oben approximiert werden. Die erste
Variante des Optional Stopping Theorems, Lemma 3.1, angewendet auf das Submartingal2
X ∨ c, c ∈ R, liefert
Xτ1n ∧τ2n ∨ c ≤ E[Xτ1n ∨ c |Fτ2n ]
woraus
E[Xτ1n ∧τ2n ∨ c |Fτ2 ] ≤ E[Xτ1n ∨ c |Fτ2 ]
folgt. Nach Definition der bedingten Erwartung ist das aber
∀ A ∈ Fτ2
E (Xτ1n ∧τ2n ∨ c) IA ≤ E (Xτ1n ∨ c) IA
(∗)
und die beiden Integranden konvergieren punktweise. Eine weitere Anwendung des Optional Stopping Theorems für die konstante Stoppzeit T , o.B.d.A. können wir für n groß
genug annehmen, dass auch τ1n ≤ T f.s., liefert
c ≤ Xτ1n ∨ c ≤ E[XT ∨ c|Fτ1n ]
und analog für Xτ1n ∧τn2 ∨ c. Mit dieser beidseitigen Abschätzung erhalten wir eine gleichgradig integrierbare Familie von Majoranten, s. Bsp. A.3. Daraus folgt, dass die Zufallsvariablen {Xτ1n ∨ c, n ∈ N} und {Xτ1n ∧τ2n ∨ c, n ∈ N} gleichgradig integrierbar sind und
wir können in (∗) den Grenzwert für n → ∞ mit dem Erwartungswert vertauschen. Wir
erhalten
Xτ1 ∧τ2 ∨ c = E Xτ1 ∧τ2 ∨ c Fτ2 ≤ E Xτ1 ∨ c Fτ2 ,
was äquivalent zu
E (Xτ1 ∧τ2 ∨ c) IA ≤ E (Xτ1 ∨ c) IA
∀ A ∈ Fτ2
(∗∗)
x 7→ x ∨ c ist eine konvexe, nicht-fallende Funktion und somit ist nach Satz 3.1 der Prozess X ∨ c
ebenfalls ein (Sub-)Martingal.
2
3.4. OPTIONAL STOPPING THEOREM
53
ist. Der Grenzübergang c → −∞ liefert (3.1) unter der zusätzlichen Bedingung, dass τ2
f.s. beschränkt ist. Dies folgt, da man in (∗∗) wiederum Grenzwert und Anwendung der
Erwartung auf beiden Seiten der Ungleichung vertauschen kann: O.B.d.A. gilt c < 0 und
man zerlege
Xτ1 ∧τ2 ∨ c = (Xτ1 ∧τ2 )+ − (Xτ1 ∧τ2 ∨ c)− .
Hier gilt der erste Term auf der rechten Seite ist unabhängig von c und (Xτ1 ∧τ2 ∨ c)− ≥ 0
konvergiert punktweise monoton wachsend gegen (Xτ1 ∧τ2 )− . Der Satz von der Monotonen
Konvergenz impliziert nun
lim E (Xτ1 ∧τ2 ∨ c) IA = E Xτ1 ∧τ2 IA
∀ A ∈ Fτ2 .
c→−∞
Ein analoges Argument gilt für die rechte Seite in (∗∗) .
Schlussendlich, ist τ2 unbeschränkt, dann ist τ2 ∧ n ein Folge beschränkter Stoppzeiten, die
τ2 approximiert. Das Ergebnis bisher liefert für n grösser als die f.s. obere Schranke von
τ1 , dass
Xτ1 ∧τ2 ≤ E Xτ1 Fτ2 ∧n .
Es ist leicht zu überprüfen, dass für ein A ∈ Fτ2 gilt A ∩ [τ2 ≤ n] ∈ Fτ2 ∧n . Daher erhält
man
E Xτ1 IA∩[τ2 ≤n] ≤ E Xτ1 ∧τ2 IA∩[τ2 ≤n] .
In diesen Ungleichungen gilt wiederum die f.s. Konvergenz und die gleichgradige Integrierbarkeit der Integranden und somit er halten wir E[Xτ1 IA ] ≤ E[Xτ1 ∧τ2 IA ]. Der Beweis von
(i) ist abgeschlossen.
(ii) Für fast sicher endliches τ1 ist τ1 ∧ n eine Folge beschränkter Stoppzeiten, die τ1
punktweise approximiert. Mit dem Ergebnis von (i) gilt
E Xτ1 ∧τ2 ∧n I ≤ E[Xτ1 ∧n IA
∀ A ∈ Fτ2 .
Das Ergebnis (3.2) folgt aus dem Grenzübergang n → ∞ und den zusätzlichen Bedingungen, die die gleichgradige Integrierbarkeit der Integranden garantieren. Wir zeigen kurz die
Art des Arguments (analog für beide Seiten in der obigen Ungleichung), das das Vertauschen von Grenzwert und Erwartung erlaubt, welches aus der punktweisen Konvergenz der
Integranden und der Konvergenz der Erwartung der Absolutbeträge folgt, vgl. Satz A.3.
Es gilt
E|Xτ1 ∧n | IA = E |Xτ1 ∧n | IA I[τ1 ≤n] + E |Xτ1 ∧n | IA I[τ1 >n]
= E |Xτ1 | IA I[τ1 ≤n] + E |Xn | IA I[τ1 >n] ,
wobei der zweite Term für n → ∞ laut Voraussetzung verschwindet
und der erste Term
wegen des Satzes von der Monotonen Konvergenz gegen E |Xτ1 |IA < ∞ konvergiert.
Daraus folgt nun die gleichgradige Integrierbarkeit und es gilt limn→∞ EXτ1 ∧t IA = EXτ1 IA .
54
KAPITEL 3. MARTINGALE
(iii) Ist das Submartingal gleichgradig integrierbar existiert eine terminale Zufallsvariable
X∞ und die Zufallsvariablen Xτ1 und Xτ1 ∧τ2 sind auch für nicht f.s. endliche Stoppzeiten
definiert. Wir betrachten wiederum die Submartingale X ∨ c, c ∈ R, und erhalten aus dem
Resultat in (i) für die endlichen Stoppzeiten τ1 ∧ n, dass
Xτ1 ∧τ2 ∧n ∨ c ≤ E[Xτ1 ∧n ∨ c|Fτ2 ] .
(∗ ∗ ∗)
Wie im Beweis zuvor betrachten wir nun zuerst den Grenzübergang n → ∞ und dann c →
−∞, wobei wir die im ersten Fall eine gleichgradig integrierbare Familie von Majoranten
aus der beidseitigen Abschätzung für t ≥ n
c ≤ Xτ1 ∧n ∨ c = Xτ1 ∧n∧t ∨ c ≤ E[Xt ∨ c|Fτ1 ∧n ] ≤ E[E[X∞ |Ft ] ∨ c Fτ1 ∧n ≤ E[X∞ ∨ c|Fτi ∧n ]
erhalten. Hier haben wir für die letzte Ungleichung die Jensen’sche Ungleichung verwendet. Die bedingten Erwartungen auf der rechten Seite sind eine gleichgradig integrierbare
Familie und wir schließen daraus, dass auch Xτ1 ∧n ∨ c, n ∈ N, eine gleichgradig integrierbare Familie bilden. Ein analoges Argument gilt auch für die linke Seite in (∗ ∗ ∗). Da
nun in (∗ ∗ ∗) die f.s. Konvergenz gilt, erhalten wir durch Vertauschen von Limes und
Erwartungswert
Xτ1 ∧τ2 ∨ c ≤ E[Xτ1 ∨ c|Fτ2 ] .
Schlussendlich liefert der Grenzübergang c → −∞ die Ungleichung (3.3). Die Argumente
hierzu sind analog zum Beweis von (i).
Eine einfache Konsequenz des Optional Stopping Theorems ist, dass das Stoppen eines
Submartingals die Integrierbarkeit des Prozesses erhält.
Korollar 3.2. Sei X ein f.s. rechts-stetiges Submartingal und τ eine beliebige Stoppzeit,
dann gilt E|Xτ ∧s | < ∞ für alle s ≥ 0.
Beweis. Wie im Beweis von Satz 3.3 erhalten wir zuerst E|Xτ ∧s | = 2EXτ+∧s − EXτ ∧s und
aus dem Optional Stopping Theorem folgt E[Xτ ∧s |F0 ] ≥ X0 und somit −EXτ ∧s ≤ −EX0 .
Das impliziert
E|Xτ ∧s | ≤ 2EXτ+∧s − EX0
und es reicht nun aus die Integrierbarkeit von EXτ+∧s zu zeigen. Nach Satz 3.1 ist X + ein positives Submartingal und es gilt nach dem Optional Stopping Theorem Xτ+∧s ≤ E[Xs+ |Fτ ].
Eine Anwendung des Erwartungswertes auf beiden Seiten der letzten Ungleichung liefert
das gesuchte:
EXτ+∧s ≤ EXs+ ≤ E|Xs | < ∞ .
Abschließend beweisen wir, dass das Stoppen eines (Sub-)Martingals auch die (Sub-)Martingaleigenschaft erhält.
3.5. DIE DOOB-MEYER ZERLEGUNG & DIE QUADRATISCHE VARIATION
55
Korollar 3.3. Sei X ein rechts-stetiges (Sub-)Martingal und τ eine Stoppzeit. Dann ist
der gestoppte Prozess X τ ein rechts-stetiges (Sub-)Martingal, d.h., es gilt
Xs∧τ ≤ E[Xt∧τ |Fs ]
f.s.
∀s ≤ t
und falls X ein Martingal ist, gilt sogar Gleichheit.
Beweis. Der gestoppte Prozess ist offensichtlich ebenfalls rechts-stetig und, da X progressiv
messbar ist, auch adaptiert. Die Integrierbarkeit des gestoppten Prozesses folgt aus Korollar
3.2. Schlussendlich gilt mit Satz 3.6 (i) und den beiden Stoppzeiten s und t ∧ T , dass für
alle s ≤ t gilt
E[Xt∧τ |Fs ] ≥ Xs∧t∧τ = Xs∧τ
mit Gleichheit falls X ein Martingal ist.
3.5
Die Doob-Meyer Zerlegung & die quadratische Variation
In diesem Kapitel legen wir einen filtrierten Wahrscheinlichkeitsraum (Ω, F, (Ft )t≥0 , P)
zu Grunde, der die üblichen Bedingungen erfüllt. Das erlaubt im Folgenden, dass jeder
Grenzwert (f.s., im Mittel, etc.) eines adaptierten Prozesses wiederum adaptiert ist und
die Ununterscheidbarkeit, die Adaptiertheit erhält. Ein Prozess bezeichnet immer einen
reellen Prozess in stetiger Zeit mit Indexmenge R+ . Oft werden wir uns auf Prozesse X
beschränken, die f.s. im Ursprung starten, d.h., X0 = 0 fast sicher. Dies ist im Allgemeinen
keine Einschränkung, da wir für beliebige Prozess X mittels Xt0 = Xt − X0 einen derartigen Prozess erhalten und die Pfadeigenschaften (Stetigkeit, Variation etc.) von X 0 und X
übereinstimmen.
In diesem Abschnitt beschäftigen wir uns vor allem mit zwei (sehr eng verwandten) Aspekten: Erstens untersuchen wir, wie auch schon bei der Brownschen Bewegung, das Variationsverhalten der Pfade von Martingalen. Zweitens, haben wir in Beispielen gesehen, z.B.,
Nt − tλ und B 2 − t, dass man aus Submartingalen durch ‘Kompensation’, d.h., Abziehen
eines geeigneten ‘wachsenden’ Objekts, wiederum Martingale erhält. In diesem Abschnitt
werden wir diese Beobachtung verallgemeinern.
Das folgende erste Resultat zeigt einerseits, dass kein (interessantes) stetiges Martingal
Pfade von endlicher Variation besitzt. Andererseits liefert es eine einfache Bedingung, die
die Existenz der quadratischen Variation eines stetigen Martingals garantiert. Die Bedingung ist überaus restriktiv und gilt nicht einmal für das Standardbeispiel eines stetigen
Martingals, nämlich die Brownsche Bewegung. Wir werden diese zweite Aussage nicht beweisen nur den Beweis etwas später skizzieren, da wir wir auf einem anderen Weg ein
stärkeres Resultat zeigen werden. Ein direkter Beweis der Aussage findet sich in [RY99,
Thm. IV.1.3].
Satz 3.7. (i) Sei M ein f.s. stetiges Martingal mit endlicher Variation, dann ist M fast
sicher konstant.
56
KAPITEL 3. MARTINGALE
(ii) Sei M ein f.s. stetiges und beschränktes Martingal, dann ist M von endlicher quadratischer Variation.
Beweis. (i) Ohne Beschränkung der Allgemeinheit (s.o.) können wir annehmen, dass
M0 = 0 f.s. und wir werden zeigen, dass dann M fast sicher konstant gleich 0 ist.
Wir nehmen zuerst an die Variation von M ist f.s. beschränkt, d.h., V[0,t] (M ) < K fast
sicher. Dann gilt für eine beliebige Zerlegung P = {0 = t0 < t1 < . . . < tn = t} wegen der
Martingaleigenschaft
n−1
n−1
i
i
hX
hX
(Mti+1 − Mti )2 .
(Mt2i+1 − Mt2i ) = E
EMt2 = E
i=0
i=0
Daraus ergibt sich die Abschätzung
h
i
2
EMt ≤ E V[0,t] (M ) sup |Mti+1 − Mti | ≤ K E sup |Mti+1 − Mti | .
i
i
Hier gilt die obere Schranke konvergiert für Verfeinerungen der Zerlegung gegen null auf
Grund des Satzes von der Dominierten Konvergenz: Der Term im Erwartungswert konvergiert wegen der Stetigkeit von M f.s. gegen null und ist durch K beschränkt. Somit gilt
Mt = 0 f.s. für alle t ≥ 0.
Ist die Variation unbeschränkt, dann definieren wir die Stoppzeiten τn := inf{t ≥ 0 :
V[0,T ] ≥ n} und betrachten den gestoppte Prozess M τn , der nach Korollar 3.3 ebenfalls
ein Martingal ist. Diese Martingale sind von beschränkter Variation und es folgt aus dem
bereits bewiesenen Mτn ∧t = 0 fast sicher für alle t ≥ 0, n ∈ N. Wegen der Stetigkeit von
M gilt τn → ∞ f.s. und daraus folgt nun, dass auch für den ungestoppten Prozess M fast
sicher Mt = 0 gilt.
Bemerkung 3.7 (Lokalisierungsprinzip). Das Beweisprinzip, das im obigen Beweis angewendet wird, eine Eigenschaft zuerst für gestoppte Prozesse zu beweisen und dann aus
τn → ∞ f.s. auf die Aussage für den nicht gestoppten Prozess zu schließen, heißt Lokalisierung und ist von außerordentlicher Wichtigkeit. Die zentrale Rolle von Stoppzeiten in
Beweismethoden unterstreicht auch die Wichtigkeit das Optional Stopping Theorems.
Definition 3.3. Wir verwenden für die quadratische Variation eines adaptierten, f.s.
(rechts-)stetigen Prozesses X – falls sie existiert – die Notation hX, Xit := L2[0,t] (X), t ≥ 0.
Der quadratische Variationsprozess hX, Xi = (hX, Xit )t≥0 ist adaptiert und startet f.s. im
Ursprung, d.h., hX, Xi0 = 0 fast sicher.
Bemerkung 3.8. Im Allgemeinen gilt, dass Existenzaussagen über die quadratische Variation auch immer miteinschließen, dass der Prozess hX, Xi eine f.s. wachsende Modifikation
besitzt, die im Falle stetiger Prozesse ebenfalls stetig ist. Wie immer, identifizieren wir
dann den Prozess mit dieser Modifikation. Es ist klar, dass die quadratische Variation in t
3.5. DIE DOOB-MEYER ZERLEGUNG & DIE QUADRATISCHE VARIATION
57
wachsend und stetig im Falle stetiger Prozesse ist, wäre sie als f.s. Grenzwert definiert. Die
quadratische Variation ist aber ein in ω globales stochastisches Konzept – im Gegensatz
zur punktweise definierten totalen Variation – und der Grenzwert hält im Allgemeinen nur
in Wahrscheinlichkeit oder im Quadratmittel. Daher ist die Existenz einer stetigen und
wachsenden Modifikation eine nicht-triviale Eigenschaft.
Das folgende Resultat zeigt, warum in diesem Zusammenhang die quadratische Variation
von großem Interesse ist, da diese den geeigneten Kompensator für das Submartingal M 2
liefert
Proposition 3.2. Sei M ein f.s. stetiges Martingal mit f.s. stetiger quadratischer Variation
hM, M i, dann ist der Prozess M 2 − hM, M i ein Martingal. Die quadratische Variation
ist der bis auf Ununterscheidbarkeit eindeutige Prozess mit dieser Eigenschaft (und den
Eigenschaften in Definition 3.3).
Beweis. Es sei P = {0 < t1 < t2 < . . .} eine Zerlegung von R+ mit je endlich vielen
Gitterpunkten in jedem endlichen Intervall [0, t]. Dann definieren wir
X
k(t)+1
Tt (M ) := (Mt − Mtk ) +
2
(Mti+1 − Mti )2 ,
(3.1)
i=0
wobei k(t) so gewählt ist, dass tk ≤ t < tk+1 , und es gilt Tt (M ) konvergiert gegen hM, M it in
Wahrscheinlichkeit, wenn die Gitterweite |∆| der Zerlegung auf [0, t] gegen null konvergiert.
Dann erhält man
E[Tt (M ) − Ts (M )|Fs ] =
X
k(t)−1
= E[(Mt − Mtk(t) ) − (Ms − Mtk(s) ) |Fs ] +
2
2
E[(Mti+1 − Mti )2 |Fs ]
i=k(s)
X
k(t)−1
=
E[Mt2
−
Ms2
+
Mt2k(t)
−
Mt2k(t)
− 2Mt Mtk(t) + 2Ms Mtk(s) |Fs ] +
E[(Mti+1 − Mti )2 |Fs ] .
i=k(s)
Mit allen gemischten Termen verfährt man folgendermaßen, indem man die Martingaleigenschaft benutzt:
E[Mt Mtk(t) |Fs ] = E[E[Mt Mtk(t) |Ftk(t) ]|Fs ] = E[Mtk(t) E[Mt |Ftk(t) ]| Fs ] = E[Mt2k(t) |Fs ] .
Somit werden alle gemischten Terme zu Quadraten, die sich in der Summation passend
kürzen und man erhält
E[Tt (M ) − Ts (M )|Fs ] = E[Mt2 − Ms2 |Fs ]
⇔
E[Mt2 − Tt (M )|Fs ] = Ms2 − Ts (M ) ,
d.h., der Prozess Mt2 − Tt (M ) ist ein Martingal. Wir betrachten nun den Grenzwert (in
Wahrscheinlichkeit), der laut Voraussetzung existiert und zeigen dieser ist ebenfalls ein
Martingal. Dazu verwenden wir wiederum das Lokalisierungsprinzip.
58
KAPITEL 3. MARTINGALE
Ist das Martingal M beschränkt, dann ist auch Tt (M ) eine in Lp (P), p beliebig, beschränkte
Familie und daher gleichgradig integrierbar und es folgt für alle A ∈ Fs
lim E (Mt2 − Tt (M )) IA = E (Mt2 − hM, M it ) IA ,
|∆|→0
lim E (Ms2 − Ts (M )) IA = E (Ms2 − hM, M is ) IA .
|∆|→0
Daher gilt Mt2 − hM, M it ist ein Martingal. Falls M unbeschränkt ist, definieren wir die
Stoppzeiten τn := inf{t > 0 : |Mt | ≥ n oder |hM, M it | ≥ n} mit τn → ∞ f.s. und M τn ist
ein beschränktes Martingal. Daher ist auch
n
n
(M τ )2 − hM τn , M τn i = (M τ )2 − hM, M iτn
ein Martingal, wobei die Äquivalenz hM τn , M τn i = hM, M iτn eine Konsequenz des Optional
Stopping Theorems und von Satz 3.7 (i) ist. Nun schließt man auf die Konvergenz der (bedingten) Erwartungswerte aus folgenden Eigenschaften: Wir haben punktweise Konvergenz
der einzelnen Terme, da τn → ∞ f.s., und aus demselben Grund konvergieren auch |Mτn ∧t |2
und |hM, M iτn ∧t | monoton wachsend gegen |Mt |2 bzw. |hM, M it |. Aus Satz A.3 folgt die
gleichgradige Integrierbarkeit und somit die Konvergenz der (bedingten) Erwartungswerte.
Schlussendlich zeigen wir noch die Eindeutigkeitsaussage. Sei A ein zweiter Prozess, sodass
M 2 − A ein Martingal ist, dann folgt
Z := M 2 − hM, M i − M 2 + A = A − hM, M i
ist ein stetiges Martingal von endlicher totaler Variation3 mit Z0 = 0 fast sicher. Aus Satz
3.7 (i) folgt nun das A eine Modifikation von hM, M i ist und da beide rechts-stetig sind
folgt die Ununterscheidbarkeit.
Beweisskizze Satz 3.7 (ii). Um die Existenz der quadratischen Variation zu zeigen beginnt
man wie im Beweis zu Satz 3.2 und erhält die Martingale Mt2 − Tt (M ). Man muss nun
zeigen, dass Tt (M ) auf endlichen Intervallen [0, T ] gleichmässig in L2 (P) konvergiert, d.h.,
zu zeigen ist, die Tt (M ) bilden eine Cauchy-Folge und die Konvergenz der Cauchy-Folge
ist gleichmässig für t ≤ T (folgt aus der Doobschen Ungleichung). Aus der gleichmässigen
Konvergenz kann man dann auch auf die Existenz einer f.s. stetigen und wachsenden Modifikation schließen.
Weiters kann man auch das Lokalisierungsprinzip verwenden um die Existenz der quadratischen Variation auf nicht-notwendigerweise beschränkte Martingale ausdehnen. Wir
werden aber einen anderen – in den sich überschneidenden Ergebnissen aber äquivalenten
– Zugang wählen, s. [RY99, S. 123f], und das quadratische Variationskonzept für lokale
Martingale, s. Abschnitt 3.5.1.
3
Es ist aus der Analysis bekannt, dass die Differenz zweier wachsender Funktionen von beschränkter
Variation ist.
3.5. DIE DOOB-MEYER ZERLEGUNG & DIE QUADRATISCHE VARIATION
59
Beispiel 3.11 (Brownsche Bewegung). Die Brownsche Bewegung B ist ein stetiges Martingal mit quadratischer Variation hB, Bit = t und wir haben bereits in Beispiel 3.1 gesehen,
dass der Prozess Bt2 − t ein Martingal ist.
Das Problem mit der Existenz der quadratischen Variation im Satz 3.7 ist, dass dieser nicht
das klassische Beispiel eines stetigen Martingals, der Brownschen Bewegung abdeckt, die
ja nicht beschränkt ist. Nachfolgend werden wir diesen Makel beheben.
Definition 3.4. (a) Wir bezeichnen mit M2 bzw. Mc2 die Menge der f.s. rechts-stetigen
bzw. stetigen quadrat-integrierbaren Martingale.
(b) Wir bezeichnen mit S bzw. Sa , a > 0, die Familie aller f.s endlichen bzw. aller
f.s. durch a beschränkten Stoppzeiten. Dann ist der f.s. rechts-stetige Prozess X ein
Prozess der Klasse D, falls die Familie {Xτ , τ ∈ S} gleichgradig integrierbar ist und
X ist ein Prozess der Klasse DL, falls für jedes a ∈ (0, ∞) die Familie {Xτ , τ ∈ Sa }
gleichgradig integrierbar ist.
(c) Ein adaptierter Prozess X ist regulär falls für alle a > 0 gilt τn ∈ Sa mit τn → τ
impliziert EXτn → EXτ .
Bemerkung 3.9. Die Brownsche Bewegung ist ein Element von Mc2 und der kompensierte
Poisson Prozess ist ein Element von M2 . Weiters gilt ein Prozess der Klasse D ist auch
ein Prozess der Klasse DL und ein Prozess der Klasse D ist gleichgradig integrierbar, da
{Xt , t ≥ 0} ⊂ {Xτ , τ ∈ S}. Für die Klasse DL gilt die gleichgradige Integrierbarkeit
nur lokal, d.h., ist τ ein f.s. beschränkte Stoppzeit, dann ist der gestoppte Prozess X τ
gleichgradig integrierbar. Weiters gilt ein Prozess X ist genau dann von der Klasse DL,
wenn für alle t ≥ 0 der ‘gestoppte’ Prozess X t von der Klasse D ist.
Beispiel 3.12. Ein gleichgradig integrierbares, f.s. rechts-stetiges Martingal ist ein Prozess
der Klasse D: Aus dem Optional Stopping Theorem folgt Xτ = E[X∞ |Fτ ] und die Familie
{E[X∞ |Fτ ], τ ∈ S} ist nach Beispiel A.3 gleichgradig integrierbar. Für Martingale ist also
die gleichgradige Integrierbarkeit äquivalent zur Eigenschaft D. Für andere Prozesse muss
das nicht gelten, diese können gleichgradig integrierbar sein aber nicht von der Klasse D.
Beispiel 3.13. Wie im vorherigen Beispiel folgt sofort, dass jedes f.s. rechts-stetige Martingal ein Prozess der Klasse DL ist.
Beispiel 3.14. Ein f.s. rechts-stetiges, positives Submartingal ist ein Prozess der Klasse DL:
Aus dem Optional Stopping Theorem folgt |Xτ | ≤ |E[Xa |Fτ ]| für alle τ ∈ Sa und nach
Beispiel A.3 ist die Familie der Majoranten gleichgradig integrierbar. Dies ist vor allem
interessant für Martingale M ∈ M2 , da dann nach Proposition 3.1 der Prozess M 2 ein
positives Submartingal ist.
Beispiel 3.15. Sei M ein f.s. rechts-stetiges Martingal und A ein f.s. rechts-stetiger wachsender, adaptierter, integrierbarer Prozess, dann ist X = M + A ein Submartingal der Klasse
DL: Die Submartingaleigenschaft des Prozesses X ist klar. Aus dem Optional Stopping
Theorem und da A wachsend ist folgt
Mτ ≤ Xτ ≤ Mτ + E[Aa |Fτ ]
=⇒
|Xτ | ≤ |E[Ma |Fτ ]| + |E[Aa |Fτ ]|
60
KAPITEL 3. MARTINGALE
und wiederum bilden die Majoranten eine gleichgradig integrierbare Familie.
Wir betrachten das Martingal M 0 = M 2 − hM, M i aus Proposition 3.2. Umformen liefert
M 2 = M 0 + hM, M i und daher erhalten wir für den Prozess M 2 eine Zerlegung in ein
Martingal und einen wachsenden Prozess wie in Bsp. 3.15. Also folgt M 2 ist von der
Klasse DL, falls die quadratische Variation existiert. Weiters nach Bsp. 3.14 ist aber M 2
sicherlich von der Klasse DL, falls M quadrat-integrierbar ist.
Dies legt die Vermutung nahe, dass jedes quadrat-integrierbare Martingal M mit M 2 der
Klasse DL eine quadratische Variation besitzt. Oder umgekehrt, dass jedes Submartingal
der Klasse DL eine eindeutige Zerlegung in ein Martingal und einen wachsenden Prozess
besitzt. Die erste Vermutung lässt sich nicht direkt beweisen, die zweite aber schon. Das
Resultat ist eine Variante der Doob-Meyer Zerlegung und falls die quadratische Variation
existiert, ist sie – zumindest im stetigen Fall – Ununterscheidbar vom wachsenden Prozess
in der Zerlegung. Für den Beweis der Doob-Meyer Zerlegung sei auf die Literatur verwiesen.
Satz 3.8 (Doob-Meyer Zerlegung). Ein f.s. rechts-stetiges Submartingal X der Klasse DL
besitzt eine bis auf Unuterscheidbarkeit eindeutige Zerlegung X = M + A in ein f.s. rechtsstetiges Martingal M und einen adaptierten, wachsenden, vorhersehbaren Prozess A. Ist X
der Klasse D, dann ist A integrierbar4 und M ist gleichgradig integrierbar. Der wachsende
Prozess A ist f.s. stetig, genau dann wenn X regulär ist.
Beispiel 3.16 (Poisson Prozess). Der Poisson-Prozess Nt ist ein rechts-stetiges, positives
Submartingale und daher nach Bsp. 3.14 ein Prozess der Klasse DL. Es gilt At = λt und
die Martingaleigenschaft von Nt − λt haben wir bereits in Bsp. 3.2 behandelt.
Das folgende Korollar ergibt sich sofort aus der Doob-Meyer Zerlegung und dem zusätzlichen
Wissen, dass jedes nicht-negative, f.s. stetige Submartingal regulär ist.
Korollar 3.4. Sei M ein Martingal aus M2 , dann existiert ein eindeutiger, f.s. rechtsstetiger und wachsender, vorhersehbarer Prozess A mit A0 = 0 f.s., sodass der Prozess
M 2 − A ein Martingal ist. Falls M f.s. stetig ist, dann ist auch A f.s. stetig. Der Prozess
A heißt die quadratische Variation und wir verwenden die Notation A = hM, M i.
Beispiel 3.17 (Brownsche Bewegung). Wie bereits direkt gezeigt, ist der Prozess Bt2 − t ein
Martingal.
et = Nt − λt ein
Beispiel 3.18 (Poisson Prozess). Wie wir gesehen haben ist der Prozess N
e, N
e it = λt.
Martingal und es ist leicht zu zeigen, dass hN
4
Im Zusammenhang mit wachsenden, positiven Prozessen ist mit Integrierbarkeit des Prozesses meist
die Eigenschaft EA∞ < ∞ verbunden. Diese Eigenschaft ist aber tatsächlich äquivalent zur Integrierbarkeit
im Sinne von EhM, M it < ∞ für alle t ≥ 0, und der L1 (P)–Beschränktheit der Familie {hM, M it , t ≥ 0}.
Da nach dem Satz von der Monotonen Konvergenz gilt EhM, M it konvergiert monoton wachsend gegen
hM, M i∞ , folgt supt≥0 EhM, M it = hM, M i∞ < ∞ (L1 (P)–Beschränktheit) und somit auch EhM, M it <
∞ für alle t ≥ 0 (Integrierbarkeit). Ebenso gilt die Umkehrung, da aus monoton wachsend und beschränkt
die Konvergenz gegen einen endlichen Grenzwert folgt.
3.5. DIE DOOB-MEYER ZERLEGUNG & DIE QUADRATISCHE VARIATION
61
Da wegen der Eindeutigkeitsaussage in Satz 3.2 und Satz 3.4 im Falle stetiger Martingale
der wachsende Prozess A in der Zerlegung mit der quadratischen Variation definiert als
Grenzwert der quadrierten Inkremente – falls dieser ebenfalls existiert – übereinstimmt,
führt die Begriffs- und Notationsgleichheit hier zu keinem Widerspruch. Im Allgemeinen
ist die quadratische Variation eine Verallgemeinerung des Konzepts der quadratischen Variation im “ursprünglichem Sinne” aus Kapitel 1. Da in der Stochastischen Analysis vor
allem die Eigenschaft, dass der Prozess M 2 − hM, M i ein Martingal ist, von Bedeutung
ist und weniger die Konvergenz der Inkremente, führt dies dazu, dass normalerweise die
quadratische Variation mit dem wachsenden Prozess in der Doob-Meyer Zerlegung gleich
gesetzt wird. Im Falle, stetiger Martingale sind die Konzepte tatsächlich äquivalent und die
Existenz der Doob-Meyer Zerlegung impliziert die Existenz der quadratischen Variation im
“ursprünglichen Sinn”.5 Für Sprungprozesse gilt dies im Allgemeinen nicht.6 Ein Beweis
des folgenden Satzes, wiederum mittels des Lokalisierungsprinzips, findet sich in [KS91,
Thm. 5.8, Chap. 1].
Proposition 3.3. Für ein M ∈ Mc2 gilt hM, M i ist auch die quadratische Variation
im ursprünglichen Sinne, d.h., Tt (M ) definiert in (3.1) konvergiert in Wahrscheinlichkeit
gegen hM, M it für alle t ≥ 0. Weiters gilt für jede Stoppzeit τ , dass hM τ , M τ i = hM, M iτ .
Terminologie: Im (kurzen) Rest des Kapitels bezeichnet die quadratische Variation immer den wachsenden Prozess in der Doob-Meyer Zerlegung. In der Literatur wird die so
definierte quadratische Variation, u.a., auch als predictable quadratic variation [JS87], conditional quadratic variation [Pro04], quadratic characteristic [JS87], (natural) increasing
process [KS91, RY99] oder angle bracket [JS87, Pro04] bezeichnet. Das letztere ist im
Kontrast zum pfadweise definiertem bracket process [X, X], der ebenfalls quadratische Variation genannt wird und mit hX, Xi im Falle stetiger Martingale übereinstimmt, vgl. eine
kurze Diskussion in [Pro04, S. 122f]. Nicht genug der Verwirrung, in [Mét82, RY99] wird
der Prozess hM, M i bracket process genannt.
Die quadratische Variation ist vor allem auch deswegen von Interesse, da sich viele Eigenschaften eines Martingals durch Eigenschaften der quadratischen Variation angeben lassen
(und umgekehrt). Die Beweise der folgenden Eigenschaften der quadratischen Variation
sind Anwendungen der bisherigen Resultate (obwohl nicht immer ganz einfach) und finden
sich in, z.B., [KS91, RY99]. Da hM, M it f.s. monoton wachsend ist, existiert der punktweise Limes limt→∞ hM, M it =: hM, M i∞ ∈ R+ ∪ {∞} f.s. und hM, M i∞ ist eine messbare
Abbildung nach dem Satz von der Monotonen Konvergenz.
Proposition 3.4. Im folgende sei M jeweils ein quadrat-integrierbares, f.s. stetiges Martingal, d.h., M ∈ Mc2 .
5
Die Umkehrung ist nach Satz 3.2 klar, d.h., die Existenz einer f.s. wachsenden, stetigen quadratischen
Variation erlaubt eine Zerlegung von der Form einer Doob-Meyer Zerlegung.
6
Zum Beispiel, lässt sich für den kompensierten Poisson Prozess Nt − λt leicht zeigen, dass die Summe
der quadrierten Inkremente nicht gegen λt
P sonder f.s. gegen die Summe der quadrierten Sprunghöhen
konvergiert, d.h., der Grenzwert ist durch s≤t (Ns − Ns− )2 gegeben.
62
KAPITEL 3. MARTINGALE
(i) Die quadratische Variation ist genau dann f.s. konstant, d.h., hM, M i = 0 f.s., falls
M f.s. konstant ist, d.h. Mt = M0 f.s. für alle t ≥ 0. Genauer, die konstanten Pfadabschnitte von M und hM, M i stimmen f.s. überein, d.h., für fast alle ω ∈ Ω gilt für
alle 0 ≤ a < b < ∞, dass
∀ t ∈ [a, b]
Mt (ω) = Ma (ω)
⇐⇒
hM, M it (ω) = hM, M ia (ω)
∀ t ∈ [a, b] .
(ii) Das Martingal M ist beschränkt in L2 (P), d.h., supt≥0 EMt2 < ∞, genau dann wenn
für die quadratische Variation gilt EhM, M i∞ < ∞.
(iii) Das Martingal M konvergiert genau dann f.s. für t → ∞ falls hM, M i∞ < ∞ fast
sicher. Genauer, es gilt die Gleichheit der Mengen
ω ∈ Ω : lim Mt (ω) existiert in R = ω ∈ Ω : hM, M i∞ (ω) < ∞ .
t→∞
(iv) Die quadratische Variation von M ist genau dann deterministisch, d.h., es existiert
eine Funktion f : R+ → R+ mit hM, M it = f (t), wenn M ein Gauss-Prozess (Definition 2.1) ist. Dieser ist eindeutig durch die quadratische Variation (bestimmt eindeutig
die Kovarianzfunktion) und EM0 (bestimmt eindeutig die Mittelwertfunktion) festgelegt (Satz 2.5).
(v) (Bernstein-Ungleichung) Das Martingal M erfülle zusätzlich M0 = 0 f.s. und es existiert ein c > 0 so dass hM, M it ≤ ct f.s. für alle t ≥ 0, dann gilt für alle α > 0
α2 t
P sups≤t Ms ≥ αt ≤ e− 2c .
(vi) (Lenglart-Domination) Für jede Stoppzeit τ und alle a, b > 0 gilt
b
P supt≤τ |Mt |2 ≥ a ≤ + P hM, M iτ ≥ b .
a
(Diese Eigenschaft gilt ohne Einschränkung für alle càdlàg Martingale.)
Bemerkung 3.10. Die Aussage (ii) dieses Proposition hat einige interessante Folgerungen:
Aus EhM, M i∞ < ∞ folgt also nach Satz A.2 auch die gleichgradige Integrierbarkeit von
M . Daher existiert ein integrierbarer f.s. Grenzwert M∞ nach Satz 3.4. Weiters folgt aus
EMt2 = EhM, M it ≤ EhM, M i∞ < ∞ für alle t ≥ 0 dass supt≥0 EMt2 < ∞ und daher ist
2
< ∞. Daraus folgt
nach Satz 3.3 auch der f.s. Grenzwert von Mt2 integrierbar, d.h., EM∞
2
nun aus Satz 3.4, dass auch das positive Submartingal M gleichgradig integrierbar sind.
Das ergibt nun schlussendlich, dass aus EMt2 = EhM, M it für alle t ≥ 0 folgt
2
= EhM, M i∞ ,
EM∞
wobei das Vertauschen von Limes und Erwartungswert links durch die punktweise Konvergenz und die gleichgradige Integrierbarkeit und rechts durch den Satz von der Monotonen
Konvergenz gerechtfertigt ist.
3.5. DIE DOOB-MEYER ZERLEGUNG & DIE QUADRATISCHE VARIATION
63
Bemerkung 3.11. [Charakterisierung der Brownschen Bewegung] Aus Proposition 3.4 (iii)
folgt, dass die Brownsche Bewegung (zu gegebener Filtration) das (bis auf Versionen) eindeutige Martingal M mit hM, M it = t und EM0 = 0 ist. Diese Aussage ist ein Hinweis
darauf, dass die quadratische Variation im Zusammenspiel mit anderen charakteristischen
Grössen eines Prozesses, in diesem Fall, z.B., der Mittelwertfunktion, dazu benutzt werden
kann einen stochastischen Prozess eindeutig zu bestimmen, vgl. den Begriff des Martingalproblems in Definition 3.9.
3.5.1
Erweiterungen des Konzepts der quadratischen Variation
Mittels des Lokalisierungsprinzips kann man die Martingaleigenschaft lokalisieren und Satz
3.7 (ii) verwenden um einen allgemeinen quadratischen Variationsbegriff einzuführen.
Definition 3.5. Ein adaptierter, f.s. rechts-stetiger Prozess X heißt ein lokales Martingal,
falls eine wachsende Folge von Stoppzeiten τn , n ∈ N, existiert mit τn ↑ ∞ f.s., und für
jedes n ∈ N der Prozess X τn I[τn >0] ein Martingal ist.
Bemerkung 3.12. Ohne Beschränkung der Allgemeinheit kann in Definition 3.5 die Folge der
Stoppzeiten so gewählt werden, dass sie aus beschränkten Stoppzeiten besteht, z.B. τen =
τn ∧ n, und / oder, dass die gestoppten Prozesse X τn I[τn >0] gleichgradig integrierbar sind.
Weiters ist klarerweise jedes Martingal ein lokales Martingal.
Das zu lokalen Martingalen gehörige Zerlegungsresultat (für stetige) lokale Martingale findet sich, z.B., in [RY99].
Satz 3.9. Sei M ein f.s. stetiges lokales Martingal mit M0 = 0 f.s., dann existiert ein
eindeutiger f.s. wachsender stetiger Prozess A mit A0 = 0 f.s., so dass M 2 − A ein lokales
Martingal ist. Der Prozess hM, M i := A heißt die quadratische Variation des lokalen
Martingals. Der Prozess hM, M i ist auch die quadratische Variation ‘im ursprünglichen
Sinn’.
Die Verbindung zur Doob-Meyer Zerlegung folgt aus folgendem Resultat, s. [RY99]: Ein
lokales Martingal ist genau dann ein Martingal falls es ein Prozess der Klasse DL ist.
Ist also M ein quadrat-integrierbares lokales Martingal der Klasse DL, dann ist M ein
quadrat-integrierbares Martingal und Korollar 3.4 gilt. Weiters ist aber das lokale Martingal
M 2 − hM, M i ebenfalls ein Prozess der Klasse DL und somit ebenfalls ein Martingal. Es
folgt aus der Eindeutigkeit in Korollar 3.4, dass in diesem Falle die ‘beiden’ quadratischen
Variationsprozesse aus Satz 3.9 und Korollar 3.4 übereinstimmen.
Eine zweite Erweiterung der quadratischen Variation ergibt sich für eine Klasse von Prozessen, die aus der Struktur der Doob-Meyer Zerlegung definiert sind. Diese Prozessklasse
bildet vor allem in den Monographien [JS87, Pro04] den Ausgangspunkt der Untersuchungen.
Definition 3.6. Ein adaptierter Prozess X heißt ein Semimartingal, falls eine Zerlegung
X = M + A existiert, so dass M ein lokales Martingal und A ein Prozess von beschränkter
Variation ist.
64
KAPITEL 3. MARTINGALE
Klarerweise ist jedes Martingal ein Semimartingal und aus der Doob-Meyer Zerlegung folgt,
dass jedes f.s. rechts-stetige Submartingal der Klasse DL ein Semimartingal ist. Weiters
kann man zeigen, dass im Falle einer f.s. stetigen Semimartingals die Prozesse M und A
in der Zerlegung X = M + A ohne Beschränkung der Allgemeinheit als f.s. stetig und
eindeutig gewählt werden können.
Satz 3.10. Ein f.s. stetiges Semimartingal X = M + A besitzt endliche quadratische
Variation (‘im ursprünglichen Sinn’) und es gilt L2[0,t] (X) = hM, M it für alle t ≥ 0.
Hier bezeichnet hM, M i klarerweise die quadratische Variation des lokalen Martingals M .
Kann auf das Semimartingal X auch einer der oberen Zerlegungssätze angewandt werden, dann sind die quadratischen Variationsbegriffe natürlich wiederum verträglich, d.h.,
die Prozesse sind ununterscheidbar. Zum Beispiel, ist das Semimartingal X = M + A
ein f.s. rechts-stetiges Submartingal der Klasse DL, dann sind M und A die eindeutigen
Prozesse aus der Doob-Meyer Zerlegung.
Die Klassen der Prozesse, für welche wir bisher einen quadratischen Variationsbegriff definiert haben, d.h., quadrat-integrierbare Martingale, lokale Martingale und Semimartingale,
besitzen alle die Eigenschaft, dass eine Summe oder eine Differenz dieser Prozesse wiederum
ein Prozess derselben Klasse ist.7 Dies ist der Schlüssel um in allen Fällen die quadratische
Kovariation zu definieren.
Definition 3.7. Die Prozesse M, N seien Martingale in M2 / lokale Martingale / Semimartingale, dann ist die quadratischen Kovariation hN, M i definiert durch die Polarisationsformel
1
hN, M i := hM + N, M + N i − hM − N, M − N i .
4
Klarerweise ist die Notation mit der quadratischen Variation veträglich falls M = N , d.h.,
die‘qudratische Kovariation’ hM, M i ist jeweils gleich der qudratischen Variation hM, M i
im vorherigen Sinn
Es lässt sich im stetigen Fall auch für die Kovariation eine Konvergenz (in Wahrscheinlichkeit) der addierten multiplizierten Inkremente analog zu Proposition 3.3 zeigen. Weiters
gilt, die quadratische Kovariation ist, z.B., im Fall von Prozessen M, N ∈ Mc2 der eindeutige, adaptierte, stetige Prozess A von beschränkter Variation mit A0 = 0 f.s., sodass M N −A
ein f.s. stetiges Martingal ist und ähnliche Aussagen gelten auch im Falle rechts-stetiger
Martingale bzw. lokaler Martingale.
Es ist leicht zusehen, dass die quadratische Kovariation eine Bilinearform auf dem jeweiligen
Vektorraum der entsprechenden Familie von Prozessen ist. Prozesse M, N mit hM, N it = 0
f.s. für alle t ≥ 0 heißen daher auch orthogonal, was, z.B., im Falle von Prozessen ∈ M2
bedeutet, dass ihre Inkremente bedingt unabhängig sind.
7
Da allgemeiner beliebige Linearkombinationen derartiger Prozesse wiederum Prozesse der Klasse sind,
bilden diese Familien lineare Räume über R.
3.6. SCHWACHE KONVERGENZ VON MARTINGALEN
3.6
65
Schwache Konvergenz von Martingalen
In diesem letzten Teil untersuchen wir die Konvergenz von Martingalen im Sinne von stochastischen Prozessen im Gegensatz zur Konvergenz entlang des Zeithorizonts wie in Kapitel 3.3. Zuerst präsentieren wir hierzu kurz die entsprechenden grundlegenden Resultate.
Diese sind eine Verallgemeinerung des bekannten Konzepts der schwachen Konvergenz von
Rd -wertigen Zufallsvariablen gibt. Eine ausführliche Diskussion findet sich, z.B., in [EK86].
Im Folgenden bezeichnet E einen vollständigen, seperablen metrischen Raum und E die
von der Metrik erzeugte Borel-σ-Algebra. Weiters sind Pn und P Maße auf dem messbaren
Raum (E, E).
Definition 3.8. (a) Die Folge der Maße Pn , n ∈ N, konvergiert schwach gegen P falls
für alle stetigen und beschränkten Funktionen f : E → R gilt
Z
Z
n
lim
f dP = f dP .
n→∞
Eine Folge von Zufallsvariablen Xn , n ∈ N, mit Werten in E konvergiert schwach
gegen eine Zufallsvariable X mit Werten in E, falls die Folge der Bildmaße von Xn
schwach gegen das Bildmaß von X konvergiert.
(b) Ein Folge von Maßen Pn , n ∈ N heißt straff, wenn für jedes > 0 eine kompakte
Menge K ∈ E existiert, so dass
inf n∈N Pn (K ) ≥ 1 − .
Ein Folge von Zufallsvariablen Xn , n ∈ N, mit Werten in E heißt straff, falls die
Folge der Bildmaße straff ist.
Bemerkung 3.13. Die Zufallsvariablen Xn , n ∈ N, und X in der obigen Definition können
auf beliebigen auch unterschiedlichen Wahrscheinlichkeitsräumen definiert sein. Im Allgemeinen ist die schwache Konvergenz eine Aussage über Maße und in eine konvergente Folge
von Zufallsvariablen kann auch als ein konvergente Folge der Äquivalenzklasse aller Variationen aufgefasst werden. Klarerweise gilt, dass der schwache Grenzwert eindeutig ist. Der
Satz von Portmanteau liefert für die schwache Konvergenz weitere, zur Definition 3.8 (a)
äquivalente Bedingungen .
Den Zusammenhang von Straffheit und schwacher Konvergenz liefert der folgende Satz
[EK86].
Satz 3.11 (Satz von Prohorov). Sei E ein vollständiger, separabler metrischer Raum. Ein
Folge von Maßen Pn auf (E, E) bzw. von Zufallsvariablen Xn mit Werten in E besitzt
genau dann eine schwach konvergente Teilfolge falls die Maße bzw. die Zufallsvariablen
straff sind.
Bemerkung 3.14. In anderen Worten, besagt der Satz von Prohorov, dass Straffheit einer
Familie von Maßen äquivalent zur relativen Kompaktheit der Familie in der Topologie
66
KAPITEL 3. MARTINGALE
der schwachen Konvergenz von Maßen ist, d.h.,
R die gröbste Topolgie auf dem Raum der
Maße über (E, E), so dass die Abbildung µ 7→ f dµ stetig ist für alle f ∈ Cb (E), vgl. die
schwach∗ -Topologie in der Funktionalanalysis. Diese Topologie ist die durch die Prohorov
Metrik metrizierbar. Gilt, dass jede konvergente Teilfolge gegen dasselbe Maß / denselben
Grenzprozess konvergiert, dann sprechen wir o.B.d.A. davon, dass auch die Folge gegen
dieses / diesen konvergiert.
Der Satz von Prohorov soll nun auf eine Folge von adaptierten càdlàg Prozessen X n definiert auf filtrierten Wahrscheinlichkeitsräumen (Ωn , F n , (Ftn )t≥0 , Pn ) mit rechts-stetiger Filtration angewendet werden. Dazu werden Prozesse als Zufallsvariablen aufgefasst, die Werte in einem passenden kanonischen Wahrscheinlichkeitsraum annehmen, z.B., den Raum
der càdlàg Funktionen D(R+ , R) bzw. dem Raum der stetigen Funktionen C(R+ , R). Daher ist es zuerst notwendig, dass diese Räume die passende metrische Struktur bekommen,
so dass man auch die kompakten Mengen charakterisieren kann. Wir wollen darauf hier
nicht weiter eingehen und bemerken nur, dass man auf den beiden Räumen eine passende
Metrik definieren kann, die Skorokhod Metrik, so dass diese vollständige, metrische Räume
werden. Die Definition der Skorokhod Metrik ist eher umständlich und auch selten explizit von Nöten, da viele nützliche hinreichende Bedingungen für die Kompaktheit bekannt
sind. Im Speziellen sind folgende Bedingungen ausreichend, so dass reelle Prozess straff
sind [EK86, JS87]: für alle T, > 0 existieren ein k und ein N mit
supn≥N Pn supt∈[0,T ] |Xtn | ≥ k ≤ (3.1)
und X n erfüllt Aldous’ Kriterium, d.h., für alle T, , δ > 0 existieren ein h > 0 und ein
N > 0, so dass für jede Folge von Stoppzeiten σn mit σn < T f.s. gilt
supn≥N sup0≤s≤h Pn [|Xσnn +s − Xσnn | > δ] < .
(3.2)
Zusätzlich ist oft noch von Interesse ob Grenzprozesse f.s. stetig sind. In diesem Zusammenhang gilt, ist die Folge X n straff, dann ist jeder schwache Grenzwert einer Teilfolge genau
dann ein f.s. stetiger Prozess falls die Sprunghöhen der Prozesse auf kompakten Intervallen
in Wahrscheinlichkeit gegen null konvergieren, d.h., für alle T, > 0 gilt
n
lim Pn supt≤T |Xtn − Xt−
| > = 0.
(3.3)
n→∞
Dies bedeutet vor allem, dass der schwache Grenzwert von f.s. stetigen Prozessen ebenfalls
f.s. stetig ist.
Der folgende Satz zeigt, dass schwache Konvergenz von Prozessen das Analogon zu Konvergenz der endlich-dimensionalen Verteilungen ist, die ja eine Äquivalenzklasse von Variationen eindeutig bestimmen. Ein Beweis des folgenden Satzes findet sich, z.B., in [EK86, JS87].
Satz 3.12. (i) Konvergieren die càdlàg Prozesse Xn schwach gegen den càdlàg Prozess
X, dann konvergieren die endlich-dimensionalen Verteilungen von Xn schwach gegen
die endlich-dimensionalen Verteilungen von X.
3.6. SCHWACHE KONVERGENZ VON MARTINGALEN
67
(ii) Umgekehrt gilt, konvergieren die endlich-dimensionalen Verteilung von Xn gegen die
endlich-dimensionalen Verteilungen von X und es gilt, die Familie Xn ist straff, dann
konvergiert Xn schwach gegen X.
Wir kommen nun zur schwachen Konvergenz von Martingalen. Wir können dazu die quadratisch Variation benutzen, die einerseits ein Kriterium für die Existenz eines schwachen
Grenzwertes liefert, als auch den Grenzprozess charakterisiert. Wir bemerken, dass im Allgemeinen der Grenzwert von Martingalen nicht notwendigerweise wiederum ein Martingal
sein muss.
Satz 3.13. Sei M n eine Folge quadrat-integrierbarer Martingale. Erfüllt die Folge der
quadratischen Variationen hM n , M n i die Bedingungen (3.1) und (3.2), dann erfüllt auch
die Folge der Martingale M n die Bedingungen (3.1) und (3.2).
Beweis. Die Aussage des Satzes folgt sofort mittels der Lenglart-Domination Eigenschaft
in Satz 3.4 (f). Sei T, > 0 fest gewählt, dann wählen wir im ersten Fall a = k 2 und
b = k 2 /2 und somit gilt
Pn supt∈[0,T ] |Mtn | ≥ k ≤ + Pn hM n , M n iT ≥ k 2 /2 .
2
Da die Folge der quadratischen
(3.1)
n Variationen
erfüllt, existieren ein N und ein k, so
n
n
2
dass für alle n ≥ N gilt P hM , M it ≥ k /2 ≤ /2 und die Bedingung (3.1) folgt für
die Prozesse M n .
Die zweite Bedingung folgt analog. Aus dem Optional Stopping Theorems folgt, dass der
fn := M n − M n ein Martingal bezüglich der Filtration Fen := F n
Prozess s 7→ M
s
σn +s
σn
s
σn +s mit
n fn
n
n
n
n
f
quadratischer Variation hM , M is := hM , M iσn +s − hM , M iσn ist. Es folgt wiederum
aus der Lenglart-Domination Eigenschaft, dass für fixes , δ > 0 gilt
Pn |Mσnn +s − Mσnn | ≥ δ
≤
+ Pn hM n , M n iσn +s − hM n , M n iσn ≥ δ 2 /2 .
2
Nun erfüllt die Folge der quadratische Variationen hM n , M n i nach Voraussetzung Aldous’
Kriterium (3.2) und somit kann kann ein N, h > 0 so gewählt werden, dass die Wahrscheinlichkeit in der rechten Seite für alle n ≥ N und alle s ∈ [0, h] kleiner als /2 ist. Daraus
folgt, dass die Folge der Martingale M n ebenfalls die Bedingung (3.2) erfüllt.
Die Straffheit einer Folge garantiert nur die Existenz eines Grenzwert einer Teilfolge der
Prozesse. Die zweite Aufgabe ist es diesen Grenzwert, falls er existiert, genauer zu charakterisieren. Ein Beweis des folgenden Satzes findet sich in [JS87, IV.6.1, IX.1.1, IX.1.19].
Satz 3.14. (i) Sei M n eine gegen M schwach konvergente Folge von f.s. gleichmässig
beschränkten Martingalen, d.h., |Mtn | ≤ K f.s. für alle n ∈ N und t ≥ 0. Dann ist M
ein Martingal bezüglich der von M erzeugten Filtration.
68
KAPITEL 3. MARTINGALE
(ii) Sei M n eine gegen M schwach konvergente Folge von lokalen Martingalen mit f.s. gleichn
| ≤ K f.s. für alle n ∈ N und t ≥ 0.
mässig beschränkten Sprunghöhen, d.h., |Mtn −Mt−
Dann ist M ein lokales Martingal bezüglich der von M erzeugten Filtration.
Gilt in beiden Fällen noch zusätzlich, dass die Prozesse M n f.s. stetig sind, dann konvergiert die Folge der quadratischen Variationen hM n , M n i schwach gegen die quadratische
Variation des Grenzprozesses hM, M i.
Bemerkung 3.15. In Bezug auf die Konvergenz der quadratischen Variation ist noch anzumerken, dass in beiden Fällen des Satzes die quadratische Variation zu den Prozessen M n
und M existiert, s. Satz 3.7 und Satz 3.9. Insbesondere sei noch zu Teil (ii) dieses Satzes
zu bemerken, dass zusammen mit Bedingung (3.3) folgt, dass schwache Grenzwerte von
f.s. stetigen lokalen Martingalen wiederum f.s. stetige lokale Martingale sind.
Dieses Resultat der Konvergenz der quadratischen Variationen kann nun schlussendlich
dazu verwendet werden um den Grenzprozess M eindeutig zu charakterisieren.8 Diese
Aufgabenstellung fällt unter den Begriff des so genannten Martingalproblems. Das Martingalproblem als ein präzise definiertes eindeutiges Konzept existiert nicht in der Literatur,
sondern der Name Martingalproblem wird allgemein für Problemstellungen ähnlicher Art
verwendet: das Auffinden eines Wahrscheinlichkeitsmaßes, so dass ein Prozess oder eine
Familie von Prozessen ein Martingal (oder lokales Martingal oder Semimartingal) ist. Varianten dieses Konzepts werden ausführlich in den Monographien [EK86, JS87] behandelt.
Wir begnügen uns mit der folgenden Definition, die das Konzept im vorliegenden Fall
ausreichend darstellt.
Definition 3.9. Auf einem filtrierten messbaren Raum (Ω, F, (Ft )t≥0 ) mit rechts-stetiger
Filtration sei ein reeller càdlàg Prozess X, ein f.s. wachsender, stetiger reeller Prozess A
mit A0 = 0 f.s. und ein Maß P0 auf (Ω, F0 ) gegeben.
(a) Ein Wahrscheinlichkeitsmaß P auf (Ω, F) heißt eine Lösung des Martingalproblems
(A, P0 ) falls der Prozess X bezüglich (Ω, F, (Ft )t≥0 , P) ein lokales Martingal mit quadratischer Variation hX, Xi = A ist und PX0 = P0 gilt.
(b) Das Martingalproblem besitzt eine eindeutige Lösung, wenn es genau ein derartiges
Wahrscheinlichkeitsmaß P gibt.
Normalerweise, wird in einem Martingalproblem als der zu Grunde liegende filtrierte messbare Raum (Ω, F, (Ft )t≥0 ) ein passender kanonischer Raum gewählt, d.h., D(R+ , R) oder auch
C(R+ , R) ausgestattet mit dem kanonischen Prozess, der kanonischen σ-Algebra und der
kanonischen Filtration.
Beispiel 3.19 (Brownsche Bewegung). Auf dem kanonischen Raum C(R+ , R) ist das WienerMaß, d.h., das eindeutige Maß, so dass der kanonische Prozess eine Brownsche Bewegung
ist, die eindeutige Lösung des Martingalproblems zu At = t und P0 = δ0 , s. Bemerkung
3.11.
8
Eine weitere Möglichkeit einen Grenzprozess eindeutig zu charakterisieren ergibt sich aus der Konvergenz der endlich-dimensionalen Verteilungen in Satz 3.12, da diese ebenfalls einen stochastischen Prozess
(bis auf Variationen) eindeutig definieren.
3.6. SCHWACHE KONVERGENZ VON MARTINGALEN
69
Beispiel 3.20. Betrachtet man dasselbe Martingalproblem wie im vorherigen Beispiel auf
dem kanonischen Raum D(R+ , R), dann geht sofort die Eindeutigkeit verloren, da für Inet = Nt − t ebenfalls die quadratische
tensität λ = 1 der kompensierte Poisson Prozess N
Variation At = t besitzt. Es ist aber möglich ein restriktiveres Konzept eines Martingalproblem zu formulieren, so dass beide Prozesse auf D(R+ , R) eindeutige Lösungen eines
Martingalproblems sind.
Es gibt in der Literatur sehr viele Untersuchungen, wann Martingalprobleme eine Lösung
besitzen und wann diese eindeutig ist. Dies wollen wir an dieser Stelle nicht näher diskutieren. Zuletzt soll der folgende Satz aber zeigen, wie man aus diesem Wissen den Grenzwert
eines Martingals eindeutig charakterisieren kann.
Satz 3.15. Sei M n eine Folge f.s. stetiger lokaler Martingale und A sei ein f.s. wachsender
und stetiger Prozess mit A0 = 0. Unter den Bedingungen
(i) die Folge M n ist straff,
(ii) die Folge M0n konvergiert schwach gegen eine Verteilung P0 ,
(iii) die Folge der quadratischen Variationen hM n , M n i konvergiert schwach gegen A und
(iv) das Martingalproblem (A, P0 ) besitzt auf dem kanonischen Raum C(R+ , R) eine eindeutige Lösung P
gilt, dass M n schwach gegen P konvergiert.
Beweis. Da die Folge M n straff ist existiert zu einer Teilfolge ein schwacher Grenzwert M ,
der nach Satz 3.14 ein lokales Martingal ist. Da die schwache Konvergenz die Konvergenz
der eindimensionalen Verteilungen impliziert, folgt dass für jede konvergente Teilfolge das
Maß P die Verteilung von M0 ist. Weiters konvergieren auch die quadratischen Variationen gegen die quadratische Variation von M . Nach Voraussetzung konvergiert aber jede
Teilfolge von hM n , M n i schwach gegen A. Aus der Eindeutigkeit des schwachen Grenzwertes folgt, dass für jede konvergent Teilfolge der Grenzwert hM, M i = A erfüllt. Daraus
folgt aber, dass für jede konvergente Teilfolge die Verteilung von M das Martingalproblem
zu (A, P0 ) löst. Dieses besitzt laut Voraussetzung eine eindeutige Lösung, also stimmt der
Grenzwert jeder konvergenten Teilfolge mit der eindeutigen Lösung des Martingalproblems
überein.
70
KAPITEL 3. MARTINGALE
Anhang A
Gleichgradige Integrierbarkeit
Wir präsentieren die Bedingung der gleichgradigen Integrierbarkeit. Diese erlaubt
es von stochastischer Konvergenz auf Konvergenz im Mittel zu schliessen und wir
erhalten auch eine weitere Bedingung, die das Vertauschen von Grenzwertbildung
und Erwartungswert erlaubt.
Ein wichtige theoretische, doch eher technische Bedingung, für die Konvergenz von Mengen
von Zufallsvariablen ist deren gleichgradige Integrierbarkeit. Im folgenden sei {Xα , α ∈
M}, eine (beliebige auch überabzählbare) Familie von reellen Zufallsvariablen auf einem
Wahrscheinlichkeitsraum (Ω, F, P).1
Definition A.1 (Gleichgradige Integrierbarkeit). Die Familie {Xα , α ∈ M} heißt gleichgradig integrierbar, falls für alle > 0 ein c = c() > 0 existiert, sodass gilt
Z
|Xα | dP ≤ .
(A.1)
supα∈M
{|Xα |>c}
Die Bedingung (A.1) der Definition kann äquivalent auch als
Z
supα∈M E|Xα | I{|Xα |>c} ≤ bzw.
lim supα∈M
c→∞
{|Xα |≥c}
|Xα | dP = 0 .
geschrieben werden. Klarerweise gilt {Xα , α ∈ M} ist genau dann gleichgradig integrierbar
wenn {|Xα |, α ∈ M} gleichgradig integrierbar ist.
Beispiel A.1. Jede endliche Menge integrierbarer Zufallsvariablen ist gleichgradig integrierbar. Eine Zufallsvariable ist genau dann gleichgradig integrierbar falls sie integrierbar ist.
Endliche Vereinigungen gleichgradig integrierbarer Familien sind gleichgradig integrierbar.
Existiert zur Familie eine integrierbare Majorante, dann ist die Familie integrierbar. Existiert zu jedem Element eine Majorante und ist die Familie der Majoranten gleichgradig
integrierbar, dann ist auch die ursprüngliche Familie gleichgradig integrierbar.
1
Die Definitionen und Resultate in diesem Kapitel gelten ohne Einschränkungen auf einem beliebigen
Massraum mit endlichen Mass.
71
72
ANHANG A. GLEICHGRADIGE INTEGRIERBARKEIT
Eine wichtige Eigenschaft der gleichgradigen Integrierbarkeit ist, dass unter dieser die
Äquivalenz zwischen Konvergenz in Wahrscheinlichkeit und Konvergenz im p-ten Mittel
gilt.
Satz A.1. Sei 1 ≤ p < ∞, dann gilt eine Folge p-integrierbarer Zufallsvariablen (Xn )n∈N
konvergiert genau dann im p-ten Mittel falls diese in Wahrscheinlichkeit konvergiert und
{|Xn |p , n ∈ N} gleichgradig integrierbar ist.
Der nachfolgende Satz gibt nun notwendige und hinreichende Bedingungen für die gleichgradige Integrierbarkeit an. Vor allem sehen wir, dass die gleichgradige Integrierbarkeit
stärker als gleichmässige Beschränktheit der ersten Momente ist, doch die gleichgradige
Integrierbarkeit aus der gleichmässigen Beschränktheit der zweiten Momente folgt.
Satz A.2. Die folgenden Aussagen sind äquivalent.
(i) Die Familie {Xα , α ∈ M} ist gleichgradig integrierbar.
(ii) limc→∞ supα∈M E |Xα | − c ∧ |Xα | = 0
(iii) (Satz von de la Vallèe Poussin) Es existiert eine nicht-negative, nicht-fallende, konvexe
Funktion G auf R+ , sodass limt→∞ G(t)/t = ∞ und supα∈M EG(|Xα |) < ∞.
(iv) Die Familie {Xα , α ∈ M} ist beschränkt in L1 (P), d.h., supα∈M E|Xα | < ∞, und
absolut stetig, d.h., für jedes > 0 existiert ein δ > 0, so dass für jedes A ∈ F gilt
Z
P(A) ≤ δ =⇒
|Xα | dP ≤ ∀ α ∈ M .
A
(v) (Satz von Dunford-Pettis) Die Familie {Xα , α ∈ M} ⊂ L1 (P) ist relativ kompakt in
der schwachen Topologie, d.h., jede Folge aus der Familie besitzt eine Teilfolge Xnk
sodass ein X ∈ L1 (P) existiert und es gilt schwache Konvergenz, d.h.,
lim E[Xnk Z] = E[XZ]
k→∞
∀ Z ∈ L∞ (P) .
Beispiel A.2. Sei p > 1 dann ist jede in Lp (P)-beschränkte Menge gleichgradig integrierbar.
Beispiel A.3. Sei X eine integrierbare Zufallsvariable und {Fα , α ∈ M} eine Familie von
Teil-σ-Algebren von F. Dann ist die Familie {E[X|Fα ], α ∈ M} gleichgradig integrierbar.
Dies folgt aus der Jensen’schen Ungleichung: Die Zufallsvariable X ist gleichgradig integrierbar und daher existiert eine Funktion G, die die Bedingungen in Satz A.2 (iii) erfüllt.
Weiters gilt aber wegen zweimaliger Anwendung der bedingten Jensen’schen Ungleichung
sup EG(|Xα |) = sup EG(|E[X|Fα ]|) ≤ sup EG(E[|X| |Fα ])
α∈M
α∈M
α∈M
≤ sup E[E[G(|X|)Fα ]]
α∈M
= EG(|X|) < ∞ .
Aus Satz A.2 (iii) folgt nun auch die gleichgradige Integrierbarkeit der Familie {E[X|Fα ], α ∈
M}. Diese Aussage verallgemeinert sich sofort zu beliebigen Familien bedingter Erwartungen von Zufallsvariablen aus einer gleichgradig integrierbaren Familie.
73
Schlussendlich erhält man nun aus dem folgenden Sätzen eine Bedingungen, die die Vertauschbarkeit der Grenzwertbildung und des Erwartungswertes als eine Verallgemeinerung
des Satzes von der Dominierten Konvergenz erlaubt.
Satz A.3. Sei die Familie {Xn , n ∈ N} gleichgradig integrierbar und Xn konvergiert
schwach gegen X, dann gilt limn→∞ EXn = EX . Umgekehrt gilt, dass, falls Xn , n ∈ N,
integrierbar ist, schwach gegen X konvergiert und limn→∞ E|Xn | = E|X| gilt, dann ist
{Xn , n ∈ N} gleichgradig integrierbar.