Ellipse - Theoretische Physik I, TU Dortmund

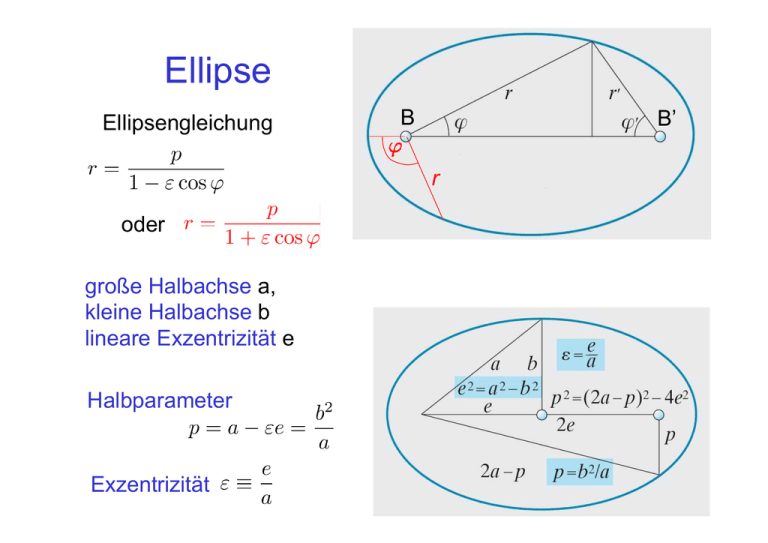
Ellipse
Ellipsengleichung
B
B’
r
oder
große Halbachse a,
kleine Halbachse b
lineare Exzentrizität e
Halbparameter
Exzentrizität
Erstes Keplersches Gesetz
•Ursprung r=0 der
Relativkoordinate
ist ein Brennpunkt
der Ellipse
B
•r=0 heißt
B’
r
Also folgt 1. Keplersches Gesetz:
Die Planeten bewegen sich auf Ellipsenbahnen, in deren
einem Brennpunkt die Sonne (genauer: der Schwerpunkt)
steht.
Keplersche Gesetze
Erstes und zweites Keplersches Gesetz bereits hergeleitet,
drittes folgt…
Historisches
Vorlesung: Gravitationsgesetz Æ Ellipsenbahnen
Historisch: Ellipsenbahnen Æ Gravitationsgesetz
Nikolaus Kopernikus
1543 (Todesjahr):
De Revolutionibus
Sonne
Nikolaus Kopernikus,
Jurist und Arzt (1473-1543)
Annahme:
Kreisbahnen
Heliozentrisches
(„Kopernikanisches“) Weltbild
Davor: Geozentrisches Weltbild;
Claudius Ptolemäus (100-175)
Tycho Brahe
Tycho Brahe,
dänischer Astronom (1546-1601)
genaue Vermessung der Planetenbahnen
mit Mauerquadrant
(noch kein Fernrohr! Æ Galilei 1610)
Johannes Kepler
Nachfolger Brahes als
Hofmathematiker in Prag
Keplersche Gesetze
Johannes Kepler,
Mathematiker (1571-1630),
Astrologe Wallensteins
Astronomica Nova (1609)
1. und 2. Gesetz
Harmonici Mundi (1619)
3. Gesetz
Abgeleitet aus Tycho Brahes Daten:
Rudolfinische Tafeln
Newton
Isaac Newton (1642-1727)
[Gerthsen, Seite 1]
Gravitation
der Apfel,
John Conduitt, Newton’s Assistant:
In the year 1666 he retired again from Cambridge to
his mother in Lincolnshire. Whilst he was pensively
meandering in a garden it came into his thought that
the power of gravity (which brought an apple from a
tree to the ground) was not limited to a certain
distance from earth, but that this power must extend
much further than was usually thought. Why not as
high as the Moon said he to himself & if so,
that must influence her motion & perhaps retain her
in her orbit, whereupon he fell a calculating what
would be the effect of that supposition
Fernwirkung der Gravitation
Æ Äpfel/Planeten
ÆNewtonsches Gravitationsgesetz,
aus Keplerschen Gesetzen abgeleitet
Botanischer Garten
Cambridge, Nachkomme von
Newtons Apfelbaum
5.4 Rutherford Streuung
α-Teilchen
(He-Kerne,
2p+2n)
Gold-Folie
ZnS-Folie
Geiger
und Marsden 1909
Rutherford Streuung
unspektakulärer Versuch,
durchgeführt von Marsden und Geiger
auf Vorschlag von Rutherford
Hans
Geiger
Ernest
Rutherford
Streuexperiment
Thomsonsches Atommodell
Erwartung damals basierend auf
Thomsonschem Atommodell
(“Plum-Pudding”)
Joseph John Thomson,
Entdecker des Elektrons (1897),
Nobelpreis 1906
Elektronen und verteilte positive Ladung
(negative Pflaumen im positiven Pudding)
Rutherford Streuung
Erwartung im
Thomson-Modell:
kaum Ablenkung der Teilchen
durch leichte Elektronen
oder durch positiven “pudding”
Ergebnis:
einige Ereignisse mit
starker Richtungsänderung
Rutherford:
It was quite the most incredible event that has ever happened to me in my life. It was almost
as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and
hit you. On consideration, I realized that this scattering backward must be the result of a single
collision, and when I made calculations I saw that it was impossible to get anything of that
order of magnitude unless you took a system in which the greater part of the mass of the atom
was concentrated in a minute nucleus. It was then that I had the idea of an atom with a
minute massive centre, carrying a charge
Qualitative Erklärung
1) vereinfachte Annahme:
zentrale elastische Stöße mα mit m?
wenn mα>>m? (z.B. wenn ? = Elektron)
dann
(kaum Impulsänderung
durch Stoß)
also alle α-Teilchen kaum gestreut
nur wenn mα<<m? , kann
auftreten, d.h. α-teilchen kommen manchmal ”zurück”
Also: α-Teilchen werden an schweren Teilchen gestreut
Qualitative Erklärung
2)
Nur wenige Streuereignisse:
Also: schwere Teilchen nehmen
“wenig Raum” ein
1),2) Æ Atommasse in Zentren
konzentriert! Æ im Kern
quantitative Erklärung folgt….
Rutherford Atommodell
Rutherfordsches Atommodell
(keine Aussage über Elektronenorte)
ÆBeginn der Kernphysik
später:
Ernest
Bohrsches Atommodell
Rutherford
(Elektronenbahnen)
(1871-1937)
Nobelpreis 1908
Quantenmechanik der Atome
(keine Bahnen mehr,
Wahrscheinlichkeitsverteilungen,
Unschärferelation!)