kq
Werbung
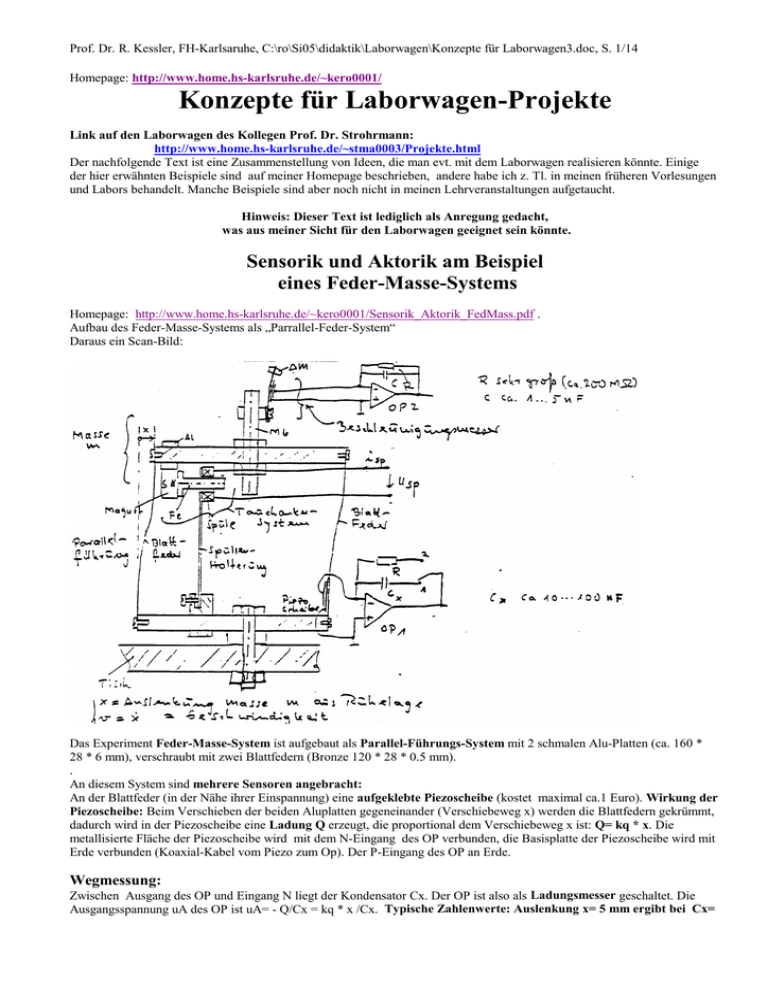
Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 1/14 Homepage: http://www.home.hs-karlsruhe.de/~kero0001/ Konzepte für Laborwagen-Projekte Link auf den Laborwagen des Kollegen Prof. Dr. Strohrmann: http://www.home.hs-karlsruhe.de/~stma0003/Projekte.html Der nachfolgende Text ist eine Zusammenstellung von Ideen, die man evt. mit dem Laborwagen realisieren könnte. Einige der hier erwähnten Beispiele sind auf meiner Homepage beschrieben, andere habe ich z. Tl. in meinen früheren Vorlesungen und Labors behandelt. Manche Beispiele sind aber noch nicht in meinen Lehrveranstaltungen aufgetaucht. Hinweis: Dieser Text ist lediglich als Anregung gedacht, was aus meiner Sicht für den Laborwagen geeignet sein könnte. Sensorik und Aktorik am Beispiel eines Feder-Masse-Systems Homepage: http://www.home.hs-karlsruhe.de/~kero0001/Sensorik_Aktorik_FedMass.pdf . Aufbau des Feder-Masse-Systems als „Parrallel-Feder-System“ Daraus ein Scan-Bild: Das Experiment Feder-Masse-System ist aufgebaut als Parallel-Führungs-System mit 2 schmalen Alu-Platten (ca. 160 * 28 * 6 mm), verschraubt mit zwei Blattfedern (Bronze 120 * 28 * 0.5 mm). . An diesem System sind mehrere Sensoren angebracht: An der Blattfeder (in der Nähe ihrer Einspannung) eine aufgeklebte Piezoscheibe (kostet maximal ca.1 Euro). Wirkung der Piezoscheibe: Beim Verschieben der beiden Aluplatten gegeneinander (Verschiebeweg x) werden die Blattfedern gekrümmt, dadurch wird in der Piezoscheibe eine Ladung Q erzeugt, die proportional dem Verschiebeweg x ist: Q= kq * x. Die metallisierte Fläche der Piezoscheibe wird mit dem N-Eingang des OP verbunden, die Basisplatte der Piezoscheibe wird mit Erde verbunden (Koaxial-Kabel vom Piezo zum Op). Der P-Eingang des OP an Erde. Wegmessung: Zwischen Ausgang des OP und Eingang N liegt der Kondensator Cx. Der OP ist also als Ladungsmesser geschaltet. Die Ausgangsspannung uA des OP ist uA= - Q/Cx = kq * x /Cx. Typische Zahlenwerte: Auslenkung x= 5 mm ergibt bei Cx= Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 2/14 100 nF Ausgangsspannung uA = -2 Volt, also ist die Sensorkonstante kq = Cx*uA/x = 100 nF *2 V/(0.005 m) = 4E-5 [Coulomb/Meter ] Geschwindigkeitsmessung mit dem gleichen Piezo: Statt des Kondensators wird der Widerstand R benutzt. Der Strom vom Piezoelement ist i= dQ/dt = kq* dx/dt = kq * v (v = Geschwindigkeit). Die Ausgangsspannung ist jetzt uA =r*i = - R * kq * v, also ist die Geschwindigkeit v= - uA/(R*kq). Typische Werte: Widerstand R = 100 kiloOhm ergibt R*kq = 100E3*kq =100E*4E-5 = 4 [Volt/(Meter/sec)]. Beschleunigungsmessung Im einfachsten Fall besteht der Beschleunigungsmesser aus einer Piezoscheibe, deren metallische Basisplatte am ihrem Rande an eine Alu-Halterung geklebt ist. Die Elektronik ist ähnlich wie bei der Wegmessung, also Ladungsverstärker, aber weil die entstehende Ladung so klein ist, ist dem Kondensator ein sehr großer Widerstand parallel geschaltet, um die „Drift“ infolge des OP-Eingangsstromes zu kompensieren. Typische Werte: C= 3.9 nF, R = 100 MegOhm Wie kommt der Messeffekt zustande? Bei Beschleunigung der Alu-Halterung verbiegt sich die Piezoscheibe etwas infolge ihrer eigenen Masse (seismische Masse). Dadurch entsteht im Piezo eine Ladung proportional der Beschleunigung Um den Messeffekt zu vergrößern, kann man eine kleine Masse auf das andere Ende der metallischen Basis der Piezoscheibe kleben, z.B. mit doppelseitig klebender Folie eine Mutter M5 draufkleben. Wichtig bei den Ladungsmessern: OP mit FET-Eingang verwenden, z.B. den TL081, nicht etwa den 714. Tauchanker-Sysstem, ( vgl obige Figur) Er besteht aus einem Permanent-Magneten, der sich relativ zu einer Spule bewegt. Typischerweise ist die Spule mit der unteren Platte verschraubt, der Magnet mit der oberen Platte. Neuerdings verwende ich die sog. Powermagnete, s. z.B. http://www.powermagnetshop.de/pi863768495.htm?categoryId=10 Dort Angebot 30 Magnete 14mm Durchmesser, Stärke 5 mm kosten ca. 30 Euro, also ein sehr preiswertes Vergnügen Damit die magnetische Wirkung sich über viele Millimeter erstreckt, z.B über 20 mm, wird auf den Magneten eine Eisenschraube M6 aufgesetzt. Sie hält sich mit der magnetische Kraft am Magneten fest. Diese Eisenschraube bewegt sich berührungslos in der Spule. Dabei gibt es zwei Wirkungen: Tauchankersystem als Geschwindigkeitsmesser Bei Relativbewegung von Spule und Tauchanker wird in der Spule ein Spannung uSp induziert: uSp= kg* v (kg = „Generator-Konstante“) Infolge der mechanischen Anordnung (der lange Eisenstab in der Spule) ist der Proportionalfaktor kg nahezu konstant, also unabhängig von der Position x. Das liegt offenbar daran, dass der von der Spule umfasste magnetische Fluss Phi nahezu linear abhängig ist von der Auslenkung x . Auf meiner Homepage wird beim Experiment Magnetlager ein solches Tauchanker-System verwendet. Es dient zur Messung der Geschwindigkeit als Istwert der unterlagerter Geschwindigkeits-Regelung: http://www.home.hs-karlsruhe.de/~kero0001/maglag5/maglag5HS.html Tauchankersystem als Aktor Fließt durch die Spule des Tauchankersystems der Strom i, so wirkt zwischen Spule und Magnet eine elektromagnetische Kraft Fel = km* iSp, mit km = „Motorkostante“. Laut Energiesatz ist km = kg. Man kann den Spulenstrom mit einer externen Spannung u erzeugen : iSp = u/Rsp ( Rsp) Spulenwiderstand, je nach Wicklung ca 10 bis 100 Ohm), folglich Leistungsverstärker nötig (s. z.B: http://www.home.hs-karlsruhe.de/~kero0001/Reglerschaltungen.html ) Durch den Spulenstrom entsteht die Kraft Fel = kg*iSp. Die externe Spannung uSp kann natürlich beliebige Kurvenform und Frequenz haben . Auf diese Weise kann man in sehr einfacher Weise die Beeinflussung eines mechanischen Schwingungs-Systems durch extern vorgegebene Kraft untersuchen, also das Thema „Erzwungene Schwingungen“ Diese Anordnung Tauchankersystem und Piezo-Sensorik am Feder-Masse-System ist sehr viel eleganter als das, was in „jedem“ physikalischen Praktikum der Universitäten (und Fachhochschulen?) geboten wird: Hier einige Google-Funde beim Suchbegriff Erzwungene Schwingungen Praktikum: http://pi.physik.uni-bonn.de/~aprakt/AP-PN-V06.pdf http://www.hausarbeiten.de/faecher/vorschau/21365.html http://www.physik.uni-essen.de/praktikum/anfaenger/M10.pdf http://www.uni-koeln.de/ew-fak/physik/Fortgeschrittenen-Vers_04.pdf Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 3/14 Dort und in zig weiteren Fundstellen wird nach wie vor das „Pohlsche Rad“ benutzt: Damals, als R. W. Pohl (1884-1976) sein System ersonnen hat, war das eine wunderbare Anordnung, wie auch seine vielen anderen Experimente. Leider hat der Versuch auch heute noch meist keinerlei Elektronik. Die Messmethodik ist witzlos und langweilig: Die Amplituden werden mit bloßem Auge an einer groben Skala abgelesen und dann schnell ins Protokollheft notiert. Irgendeine Registrierung von Kraft und Auslenkung wird wohl so gut wie nie realisiert. Außerdem kann die Kraft nur Sinusform haben. Die Phasenlage zwischen Kraft und Auslenkung kann man nur sehr grob ablesen, wieder nur mit bloßem Auge. Im Vergleich zum Pohlschen Rad ist das oben beschriebene Parallel-Führungs-System außerordentlich vielseitig. Natürlich ist die Registrierung von Kraft und Auslenkung oder auch Geschwindigkeit oder Beschleunigung möglich, die Zeitform der Kraft kann, wie schon gesagt, beliebig sein, etwa Rechteck oder Dreieck oder Rauschen oder … Eine Simulation mit variierter Erregerfrequenz (Frequenz-Sweep) findet man auf der homepage: http://www.home.hs-karlsruhe.de/~kero0001/sweepfedmas/SweepFedMas2.pdf Ganz neu (im Vergleich zum Pohlschen Rad) ist die Möglichkeit, den Spulenstrom durch die Tauchankerspule vom schwingenden System selbst zu erzeugen. Man kann also eine Rückkopplung realisieren. Besonders wirkungsvoll ist es natürlich, die vom Geschwindigkeits-Sensor (etwa. Piezo mit Widerstand am OP (s. o), oder mittels eines zweiten Tauchankersystems) gelieferte Spannung zu verwenden. Dann ergibt sich eine Kraft proportional zur Geschwindigkeit v: Fel= k*v. Je nach Spulenpolung wirkt diese Kraft in die gleiche Richtung wie v oder entgegengesetzt. Im ersten Fall ist das eine Mitkopplung, im zweiten Fall Gegenkopplung. Bei Mitkopplung ergeben sich selbsterregte Schwingungen, bei Gegenkopplung hat man eine aktive Bremse. Mit diesem Parallelfedersystem kann man auch diverse Dämpfungs-Methoden untersuchen, außer der schon erwähnten aktiven Dämpfung: Gleitreibung Man hält (mit einer ortsfesten Halterung) einen Streifen Pappe (oder ein anders Material) auf die bewegliche obere Platte. Auf diesen Dämpfungsstreifen legt man eine Masse mK (Klotz). Dan wirkt auf die bewegliche Platte die Normalkraft Fn= mK * g (g = Fallbeschleunigung) und folglich eine Gleitreibungskraft FGL = mu * Fn (mu = Gleitreibungszahl). Man wird es nicht glauben: In den Büchern über Technische Mechanik oder auch in Physik-Büchern wird selten mal der Einfluss der Gleitreibung auf Schwingungen untersucht. Drum mein Homepage-Text http://www.home.hskarlsruhe.de/~kero0001/fedmass/FedMassSchwing.pdf Ein besonderer Effekt ergibt sich, wenn auf die bewegliche Platte ein Massenklotz aufgelegt wird und man die obere Platte auslenkt und dann loslässt: Es ergibt sich zunächst Dämpfung, aber dann schwingt das System nahezu ungedämpft weiter. Simulation dazu in http://www.home.hs-karlsruhe.de/~kero0001/UebApril06.html Reibklotz auf schwingender Platte Gleitreibung in Kombination mit der Selbsterregung Bei der oben erwähnten selbsterregten Schwingung ergibt sich bei Vorhandensein von Gleitreibung ein besonderer Effekt nämlich ein sog. Chaos-Effekt: Nur wenn die Startauslenkung größer ist als ein gewisser „kritischer Wert“, ergeben sich Schwingungen mit ansteigender Amplitude, unterhalb dieses kritischen Wertes schwingt das System eine Zeit lang, dann aber nehmen die Amplituden wieder ab und die Schwingung kommt völlig zur Ruhe. Diese Amplituden-Abnahme erfolgt überraschenderweise nicht so, wie man es von den üblichen gedämpften Schwingungen kennt, nämlich nicht wie bei den exponentiell gedämpften Schwingung mit „nach innen“ gewölbten Einhüllenden der Amplituden, sondern die Einhüllende der Amplituden ist „nach außen gewölbt“ . Auf der Homepage habe ich mehrere andere Experimente mit Chaos-Effekt beschrieben: http://www.home.hs-karlsruhe.de/~kero0001/WiChaos/WiregChaos2.pdf http://www.home.hs-karlsruhe.de/~kero0001/hub60/hub_60.html http://www.home.hs-karlsruhe.de/~kero0001/PaddelChaos/PaddelChaos.html http://www.home.hs-karlsruhe.de/~kero0001/Drehos/DREHOSZ5s.html Bei allen diesen Beispielen ist die Gleitreibung der Lager die Ursache für den Chaoseffekt. Tilger als Schwingungsdämpfer Dazu verweise ich der Einfachheit halber auf die homepage: http://www.home.hs-karlsruhe.de/~kero0001/UebApril06.html Die Wirkung von Tilgern wird selten mal in einem Lehrbuch erwähnt. Dabei können Tilger sehr nützlich sein, wie man am Beispiel der Millenium-Brücke London oder dem Hochhaus Taiwan sehen kann: http://www.isd.uni-hannover.de/fileadmin/eroeffn-kolloq/gerasch-folien.pdf Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 4/14 Weitere Sensorik DMS- Biegebalken Taktile Roboterhand http://www.home.hs-karlsruhe.de/~kero0001/takthand/takth5.html Modellversuch zur „Servolenkung“ (Lenkkraftverstärker) Das Experiment habe ich noch nirgends beschrieben. Prinzip: Ein mit einer DMS-Vollbrücke aufgebauter DrehmomentSensor ist an eine Welle (Durchmesser 6 mm) geschraubt, diese Welle hat infolge einer als Reibbremse angeklammerter Laborklemme so viel Reibung, dass man die Welle mit der Hand kaum drehen kann. Das vom DMS-Sensor gelieferte Spannung wird verstärkt und speist über einen Leistungs-Spannungsfolger einen an die Welle angeschlossenen Getriebemotor.- Auf diese Weise kann man mit winziger Anstrengung die Welle drehen. Der Gesamtverstärkungsfaktor ist ein Maß für die noch notwendige Körperkraft: je größer die Verstärkung, umso weniger Körperkraft ist nötig. Kraftsensor Halb-professioneller Biegbalken zur Messung von Kräften unabhängig vom Ort der Krafteinwirkung. Dieser Biegebalken wurde von einem Studenten privat hergestellt, von mir mit DMS-Brücke beklebt. Damit könnte man allerlei Experimente zur Kraftmessung durchführen. Beispiele: Messung der Wirbelstromkraft: auf den Kraftsensor wird ein Dauermagnet montiert, vor diesem Magneten bewegt sich eine metallische Scheibe, etwa angetrieben von einem Elektromotor. Die Wirbelstromkraft ist abhängig vom Abstand zu Scheibe, von der Dicke und dem Material und der Geschwindigkeit der Scheibe (Eine alternative Methode zur Messung der Wirbelstromkraft s. Seite 14) Messung der Lagerkräfte bei einem schwingenden Pendel, Vergleich mit numerisch simulierten Werten. Ein einfaches Experiment mit Überraschungseffekt: An eínem DMS-Kraftsenor hängt an einer langen weichen Feder eine Kugel. Der Kraftmesser misst die Federkraft, also das Produkt D* Federlängerverlängerung (D= Federkonstante) , also misst der Kraftmesser (indirekt) die Position der Kugel. Die Kugel hebt man etwas hoch und lässt sie los. Überraschenderweise ist die Amplitudenverlauf dieser Feder-Masse-Schwingung NICHT etwa eine Exponentialfunktion exp(-t/tau) (wie in jedem Lehrbuch zur Physik und Technischen Mechanik behauptet), sondern anfangs starke Dämpfung, später fast keine Dämpfung mehr. Die Erklärung: Die Reibungskraft ist nicht etwa proportional der Geschwindigkeit, sondern proportional v*abs(v), nämlich turbulente Luftreibung. Eine Simulation einschließlich Messwerten s. Homepage (dort allerdings Messungen mit einem Piezo-Biegebalken, daher Nachteil: Driftproblem infolge Eingangsstrom des OP). http://www.home.hs-karlsruhe.de/~kero0001/kugelanfeder/KugelAnFeder2.pdf Optoelektronische Sensoren Man baue sich einen Lichtsenor aus Fotodiode und Operationsverstärker und teste damit allerlei Lichtquellen, die in unsrer Umgebung vorhanden sind: Glühlampe, Glühlampe mit Dimmer betrieben, Leuchtstofflampe, die Signallampen von Elektrogeräten (Lötkolben, Bügelleisen, Steckerleiste,…), Straßenlaternen,…. . Etwa Thema Glühlampe: Zeigt deren Licht überhaupt eine gewisse Welligkeit? Wenn ja, sind das 50 Hertz oder was anderes? Würde zusätzlich zum Licht auch die Versorgungs-Spannung der Glühlampe gemessen (also die Netzspannung), dann ergibt sich die Frage: Welche Phasenlage hat die Helligkeit bezogen auf die Wechselspannung? Man überlege sich ein mathematisches Modell zur Glühlampe. Der Widerstand ist natürlich abhängig von der Temperatur und damit auch von der Spannung. Die Wärmeabgabe der Glühlampe ist proportional der 4. Potenz der absoluten Temperatur (StefanBoltzmann-Gesetz). Also ergibt sich (mal wieder!) eine nichtlineare DGL. Drum findet man dies alltägliche Beispiel in keinem Lehrbuch! Einige Experimente mit optoelektronischen Sensoren wurden auf der Homepage beschrieben: Beim Experiment „Kugel auf Felgenrad“ dient die Kombination Glühlampe, Solarzelle, Operationsverstärker zu Messung der Kugelposition. http://www.home.hs-karlsruhe.de/~kero0001/Felgenrad/FelgenradHS.html Beim Experiment „Magnetlager“ wird eine Dual-Reflex-Lichtschranke verwendet zur Messung der Position des Eisenjoches (Leuchtdioden, Fototransistoren): http://www.home.hs-karlsruhe.de/~kero0001/Magnetlager.html Beim Experiment „Relais-Dynamik“ einseitige Reflex-Lichtschranke http://www.home.hs-karlsruhe.de/~kero0001/relais/relaisdynamik.html Beim Experiment „PLL-Drehzahlregelung“ Leuchtdiode plus Fototransistor plus rotierende Schlitzscheibe. http://www.home.hs-karlsruhe.de/~kero0001/PLL.html Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 5/14 Beim Experiment „Unwuchtsynchronisation“ ebenfalls Lichtschranke und Schlitzscheibe: http://www.home.hs-karlsruhe.de/~kero0001/Unwucht/Unwuchtsyn.html Beim Experiment „Lichtstrahlverfolger“ zwei Fototransistoren: http://www.home.hs-karlsruhe.de/~kero0001/Lichtstrahlverfolger.html Man überlege sich eine Lichtschranken-Schaltung zur vorzeichenrichtigen Drehzahlmessung. Ziel: Analogspannung proportional der Drehzahl, positiv bei Drehung rechts herum, negativ bei Drehung links herum. Wirbelstrom-Sensor Wenn man von Google die Suchbegriffe Wirbelstromsensor und/oder Näherungssensor oder Metalldetektor eingibt, ergeben sich sehr viele Fundstellen über diese nützlichen und preiswerten Geräte. Es ist lehrreich, solche Sensoren zu Experimentierzwecken selbst zu bauen: Man baue einen LC-Osizillator auf (z.B. als LC-Parallelschwingkreis mit OPSchaltung ( http://www.home.hs-karlsruhe.de/~kero0001/sinus/sinus.html ) oder auch mit Transistorschaltung. Eine solche Schaltung kann als Wegsensor verwendet werden. Hält man die Spule in die Nähe von Metall, so werden im Metall Wirbelströme induziert. Diese haben zwei Wirkungen auf den Oszillator: Infolge des Ohmschen Widerstands entziehen die Wirbelströme dem Oszillator Energie und gleichzeitig beeinflussen sie die Frequenz des Oszillators. Je näher das Metall zur Spule ist, umso mehr werden die Amplituden gedämpft. Durch Gleichrichtung und Tiefpass gewinnt man eine Spannung, die von der Position des Metalls abhängt. Bei einer langen Spule mit einem in die Spule eintauchenden Stab aus Metall ergibt sich ein berührungsloser Positions-Sensor für die Eintauchtiefe des Metallstabes. Wenn man sich Mühe gibt, kann man die Kennlinie linearisieren. – Die Frequenz des Oszillators ist ebenfalls von der Position und den Eigenschaften des Metalls abhängig. Bei ferromagnetischem Material wird die Frequenz kleiner, bei allen andere Metallen wird die Frequenz größer (warum eigentlich??) Mikrofon als Sensor Bekanntlich gibt es sehr preiswerte Mikrofone (Elektret-Kondensator-Mikrofone), die sehr klein sein können (z.B Durchmesser bis herab zu etwa 4 mm, Länge auch nur wenige mm). Mit einer einfachen OP-Schaltung gewinnt man eine Spannung proportional dem Schalldruck. Damit kann man bis z.B. 60 kHz messen. Natürlich kann man sich allerlei Versuche einfallen lassen, bei denen das Mikrofon Töne misst. Auf der Homepage findet man Messungen von Vokalen mit der Koblitz-Platine, ausgewertet im Zeitbereich und im Frequenzbereich mit Matlab: http://www.home.hs-karlsruhe.de/~kero0001/vokale/vokale.html Weitere Experimente zur Akustik bieten sich an: stehende Wellen in Rohren, Einfluss des Wandmaterials auf den Reflexionsfaktor, Einfluss der Gasart auf die Schallgeschwindigkeit, Dynamik des Einschwingvorgangs und des Ausschwingvorgangs beim Ein- und Ausschalten des Erregersinus. Experimente mit Helmholtz-Resonatoren: Ein Mikrofon befindet sich in einem Hohlraum, z.B. einer gewöhnlichen Glasflasche, in der Nähe der Flasche steht ein Lautsprecher, mit dem man Sinustöne erzeugt. Man findet eine Resonanzfrequenz fres. Diese Helmholtzfrequenz ist fres=1/(2*pi) * c* sqrt(A/(V*L)), mit c= Schallgeschwindigkeit des Gases im Hohlraum, A = Querschnittsfläche des "Loches", L= Länge des Loches, V= Volumen des Hohlraums Das zugehörige mathematische Modell ist wie folgt: Die Masse des Gases im Flaschenhals ist die Masse m, das Volumen der Flasche wirkt als Feder D (adiabatische Zustandsänderung) , das ergibt die Formel f = sqrt(D/m) /(2*pi). Beim oben beschriebenem Experiment findet man, dass es bei Resonanz innerhalb der Flasche sehr viel lauter ist als außerhalb der Flasche (wieso eigentlich?). Wenn man den Erregersinus nur eine endliche Anzahl (z.B. 50) von Sinusperioden wirken lässt, steigt zunächst der Schalldruck in der Flasche an. Nachdem Abstellen des Sinuserregers schwingt die Luft in der Flasche noch weiter, natürlich gedämpft. Die Frage ist z.B. von was hängt die Dämpfung ab? Mit welcher Frequenz schwingt die Luft weiter? Ist das die Erregerfrequenz? Vergl. den oben erwähnten Ein- und Ausschwingvorgang bei stehende Wellen in Rohren. Bekanntlich spielen Helmholtz-Resonatoren im Mundbereich bei der Vokalbildung unsrer Stimme eine wichtige Rolle (Stichwort Formanten). Man lasse sich eine elektronische Schaltung einfallen, mit der die Luft in der Flasche zu selbsterregten Schwingungen angeregt wird. (Rückkopplungs-Pfeifen). Dabei das Problem, dass die Luft in der Flasche nicht nur die Helmholtz-Frequenz hat, sondern infolge stehender Wellen in der Flaschenluft auch andere Resonanz- Effekte auftreten. Man muss also dafür sorgen, dass nur die gewünschte Helmholtzfrequenz zur Selbsterregung führt. Methode: z.B. aktiver Tiefpass 2. Ordnung, zusätzlich aktiver Phasenschieber. Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 6/14 Mikrofon als Sensor für die Beschleunigung schwingender Flächen. Außer für akustische Experimente kann man ein Mikrofon auch für die Untersuchung schwingender Oberflächen anwenden. Einfachstes Beispiel: Man nehme eine Kaffee-Tasse und schlage mit einem harten Gegenstand auf die Wand der Tasse. Jedermann weiß, dass die Tasse durch den Schlag zu Tönen angeregt wird, die man sehr deutlich hört. Die Frage ist natürlich: Wie schwingt denn eigentlich eine solche Tasse? Ohne Elektronik kommt man da nicht weiter. Mit zwei Mikrofonen, mit DigitalOszi (etwa Koblitzplatine) wird man da bald schlauer. Spektralanalyse (FFT) der Mikrofonsignale. Man erkennt, dass im dem Klang der angeschlagenen Tasse viele Frequenzen enthalten sind. Die sind aber nicht etwa „harmonisch“ , sondern die Oberschwingungen sind keinesfalls ganzzahlige Vielfache einer Grundschwingung, wie es etwa beim Klang eines Geigentones oder Gitarrentones oder Flötentones, oder auch eines menschlichen Vokals ist Grund für die Nichtharmonizität des Tassen-Schwingung: Die zugrunde liegende DGL der Biegschwingungen ist eine partielle DGL 4. Ordnung, während es sich bei den anderen um DGln 2. Ordnung handelt. Statt der angeschlagenen Tasse kann man die Schwingungen vielerlei anderer Objekte mit Mikrofonen „erforschen“. Statt die Körper einfach anzuschlagen, kann man die Töne (mit einem geeigneten Aktor) auch gezielt in einer der Resonanzfrequenzen erregen und mit dem Mikrofon die Oberfläche abhorchen. Man betreibt also „Modalanalyse“. Als Aktor für Experimente dieser Art kann man z.B. eine Piezoscheibe auf die Oberfläche kleben. Beim Anlegen einer Spannung, etwa einer Sinusspannung, verbiegt sich die Piezoscheibe etwas und regt auf diese Weise den ganzen Körper zum schwingen an. Über ein Experiment mit Schwingungsanregung einer Stahlplatte mit Piezoscheibe s. S. 10 Man überlege sich Experimente, die zeigen dass das Mikrofon vor einer schwingenden Fläche die Beschleunigung der Fläche anzeigt, nicht etwa die Geschwindigkeit. Tonabnehmer als Sensor und als Aktor Tonabnehmer aus der Schallplattentechnik (z.B. sog. Kristall-Tonabnehmer, also piezoelektrische Tonabnehmer ) lassen sich ebenfalls gut als Sensoren und als Aktoren verwenden, natürlich nur für winzige Kräfte). Leider sind Tonabnehmer heute wohl nicht mehr im Handel Füllstands-Sensor Bei meinen Experimenten zur Füllstandsregelung verwende ich kapazitiv arbeitende Füllstands-Sensoren, die eine Spannung proportional der Füllhöhe des Wassers in den Tanks liefern: http://www.home.hs-karlsruhe.de/~kero0001/F%FCllstandsregelung_n.html Dort findet man die Beschreibung der Wirkungsweise und die elektronische Schaltung . Jetzt folgt die stichwortartige Beschreibung einiger Experimente Gekoppelte Feder-Masse-Systeme, Stichwort Modalanalyse Das ganz am Anfang beschriebene Parallelfedersystem kann man natürlich in vielfältiger Weise mit anderen Parallelfedersystemen zu gekoppelten Feder-Masse-Systemen verbinden, z. mehrere Systeme übereinander, oder mittels zusätzlicher Koppelfedern nebeneinander oder auch eine Kombination von übereinander und nebeneinander. Wozu soll das gut sein?? Zur „Motivation“ zu diesem Thema lasse man von Google suchen: gekoppelte Schwingungen, physikalisches Praktikum. Es ergeben sich über 700 Fundstellen. Was findet man darin? Den klassischen Versuch mit zwei über eine Feder gekoppelten identischen(!) reibungslosen (!) Pendeln. Man hat den Eindruck, dass an „allen“ Universitäten und Fachhochschulen dieser Versuch durchgeführt werden muss. Die Messtechnik: Bei den meisten Laboranleitungen wird nur mit Stoppuhr die Periodendauer gemessen. Dabei die drei Sonderfälle der Startbedingungen: beide Pendel gleiche Startauslenkung, dann beide Pendel entgegensetzt gleiche Startauslenkung, dann ein Pendel ausgelenkt, das andere in Ruhelage. Das Ziel dieser einschläfernden Versuche ist, die Theorie zu bestätigen. Aber bitte nur kleine (!) Startauslenkungen verwenden, denn für große Amplituden hat man ja keine Theorie! Diesen Versuch gibt es schon seit (mindestens) 100 Jahren! Sagt die Laboranleitung irgendetwas darüber aus, wie man den Versuch verallgemeinern kann, z. B. verschiedenartige Pendel, z.B. mehr als zwei Pendel, z.B. Pendel mit Reibung ? Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 7/14 Zusammengefasst: Das didaktische Ziel des Experiments gekoppelte Pendel ist es, einige der Erscheinungen zu untersuchen, die durch die Kopplung von zwei Schwingungs-Systeme auftreten. Leider aber wird mangels Sensorik und mangels numerischer Mathematik nur der einfachste Fall untersucht, der gerade noch analytisch, also ohne numerische Mathematik behandelbar ist. Diese Thematik gehört in den Bereich der „Modalanalyse“, also die experimentelle oder auch theoretische Untersuchung von „Schwingungs-Moden“. Mathematische Stichworte Eigenwerte, Eigenvektoren Jetzt einige Beispiele zu Experimenten und Simulationen mit den oben erwähnten gekoppelten Systemen, die man mit dem Parallel-Feder-System realisieren kann. Mehrere Beispiele findet auf dieser Homepage: Die mathematische Modellbildung und die daraus sich ergebende Computer-Simulation: http://www.home.hs-karlsruhe.de/~kero0001/FedMas3/FedMasKet3h.html Eine Simulation zur experimentellen Modalanalyse: http://www.home.hs-karlsruhe.de/~kero0001/demodal/DemoModal_3.html Ein Beispiel zur experimentellen Realisierung mit gekoppelten Parallel-Feder-Systemen, Messungen mit der Koblitz-Platine, Auswertungen mit Tephys. http://www.home.hs-karlsruhe.de/~kero0001/kobmod/kobmod1.html Solche Art Experimente habe ich schon seit Jahren in meiner damaligen Physik für Semester F4 (damals Feinwerktechnik) durchgeführt, allerdings mit anderen Oszilloskopen. Ein weiteres experimentelles Beispiel, ebenfalls mit Tephys: http://www.home.hs-karlsruhe.de/~kero0001/Tepmod/ExpModal4Etag_Tephys.pdf Schließlich mehrer Beispiele zur experimentellen Modalanalyse, die ich in den Jahren um 1987 mit Hilfe des FFTAnalysators ONO SOKKI und einer selbstprogrammierten Software ausgeführt habe: http://www.home.hs-karlsruhe.de/~kero0001/modal/modal4com.html Darin unter anderem die Modalanalyse der (sehr schwingfreudigen) Treppe im Physik-Bau unsrer Fachhochschule. Die Dateien kann man runter laden. Die Animation der Schwingungsformen funktioniert heute noch auf jedem(?) PC. Experimente mit Ultraschall-Piezo-Dosen In meiner Vorlesung „Physikalische Messtechnik“ (damals Semester F7, F8) habe ich einige Experimente mit solchen Ultraschall-Piezo-Dosen behandelt, unter anderem auch mit dem FFT-Analysator ONO SOKKI. Auf der Homepage findet sich nichts von den damaligen Experimenten. Aber ich kann mir vorstellen, dass solche Experimente gut geeignet wären für den Laborwagen Einzelheiten in meinen damaligen (Papier-) Texten: Seiten 30 bis 35 und Seiten Piezo-XEFR-1 bis PiezoXEFR-7. Hier einige Stichworte Aufbau der Piezo-Dosen, geeignet als Sender und Empfänger. Eigenfrequenzen und Schwingungsformen der Abstrahlfläche (unter anderem durch Aufstreuen von Sand (ChladniKlangfiguren) Bestimmung der Schwingungsformen mit aufgesetzter Nadel eines Piezo-Tonabnhmers, Impulsbetrieb eines Ultraschall-Sender-Empfänger-Systems. Zeitbereich und Spektalbereich. Dabei ein Überraschungseffekt: Der Sender wird zwar mit nur einer einzigen Sinusperiode der Eigenschwingung (ca 30 kHz) angeregt, das Empfänger-Signal hat aber eine überraschend komplizierte Zeitform: Abgesehen von der (natürlich erwarteten Zeitverschiebung infolge Laufzeit des Schalls) antwortet der Empfänger mit ca 17 Perioden ansteigenden Sinusamplituden, gefolgt von allmählich abnehmenden Sinusamplituden. Zur Deutung dieser Erscheinungen zunächst ein Analogie-Experiment: Mit LC-Bandpässen (statt des Piezosystems), dann wieder Experimente mit auf die Abstrahlfläche aufgesetzten Tonabnehmer-Nadel. Dann experimentelle Aufnahme des komplexen Leitwertes Y = Strom durch Spannung eines Piezoelementes. Dabei wieder ONO-SOKKI benutzt ( Rauschen als Spannung am Piezo, Strom-Messung mit einer Transistor-Basis-Schalung). ONO SOKKI liefert Betrag und Phase des Leitwerts Y, auch als komplexe Ortskurve dargestellt. Deutung dieser experimentellen Leitwert-Kurve durch ein mathematisches Modell. Das liefert ziemlich genau die experimentellen Werte. Diese Simulation findet man auf der Homepage: http://www.home.hs-karlsruhe.de/~kero0001/piezo/piezo4.pdf In meiner damaligen Elektronik-Vorlesung und im zugehörigen Labor habe ich eine Schaltung behandelt, mit der man die Geschwindigkeit der eines bewegten Körpers mit Hilfe des Doppler-Effektes messen kann. Eine in Resonanz (ca. 30 kHz) betriebene Ultraschall-Dose sitzt auf dem bewegten Körper, dessen Geschwindigkeit gemessen werden soll. Die von einem ruhenden Empfänger (z.B. eine ähnliche Ultraschalldose) gemessenen Frequenzen werden multiplikativ in den Bereich tiefer Frequenzen verschoben. Dadurch wird die durch die Geschwindigkeit verursachte relative Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 8/14 Dopplerverschiebung, bezogen auf die absolute Frequenz, sehr viel größer und kann mit einem Frequenz-Spannungs-Wandler gemessen und registriert werden. Z.B. kann man auf diese Weise die Schwingung eines Biegebalkens, auf dem die abstrahlende Ultraschall-Piezo-Dose sitzt, gemessen werden. Der Einfachheit halber füge ich ein Scan-Bild aus meiner damaligen Elektronik-Vorlesung ein: Die zeigt nur das Prinzip. Die Frequenz der Ultraschalldose ist 30 kHz. Der Vorlesungstext nimmt 20 kHz an. Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 9/14 Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 10/14 Messung von Realteil und Imaginärteil mit der „Sinus-Cosinus-Technik“ Darstellung als komplexe Ortskurve. Auf dieser Seite nur das Prinzip und eine Schaltung zum Kalibrieren der Elektronik. Als Untersuchungsobjekte habe ich z.B. ein „Kabel-Modell“ benutzt, das aus mehreren gekoppelten Spulen (als Längs-Impedanzen ) und Kondensatoren (als Querleitwerte) besteht Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 11/14 Ein Beispiel, wie man trotz Anwesenheit sehr starker Störsignale den Frequenzverlauf von Realteil und Imaginärteil messen kann. Als „Strecke“ diente eine Stahlplatte, die mit aufgeklebter Piezoscheibe sinusförmig erregt wurde. Als (bewusst störempfindlicher) Empfänger diente ein über die Platte gehaltenes Mikrophon (entspricht Beschleunigungsmesser, s.o.) . Als Störsignale diente laute Musik aus einem Tonbandgerät (z.B. „Mexico“ von Les-Humphries). Oder zusätzlich möglichst lautes Schreien der Studenten. Trotz aller Störsignale konnte man der Frequenzverlauf von Realteil und Imaginärteil messen. Das war ein sehr überzeugendes Experiment für raffinierte Messtechnik. Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 12/14 Experimentier-Aufbau einer Auswuchtmaschine Eine weitere Anwendung der Messung von Realteil und Imaginärteil, auch bei Anwesenheit von Störsignalen, findet sich im Experiment Auswuchtmaschine.. Davon ( zum Einstieg ) die erste Seite meines Vorlesungstextes. Hinweis: Diese Auswuchtmaschine funktioniert auch heute noch. Leider findet sich im Studiengang Sensorsystemtechnik niemand, der sich für diese Thematik interessiert. Die Auswertung der Mess-Signale erfolgt mit raffinierter Mathematik, u.A. MatrizenRechnung, wäre gut für Matlab geeignet Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 13/14 Experimente mit einem „Zentrifugen-Lager“ und Simulationen Dies Experiment habe ich zwar in der Vorlesung Physikalische Messtechnik behandelt. Es ist aber noch nicht auf der Homepage beschrieben. Motivation: Eine handelsübliche Wäscheschleuder, getrennt von der eigentlichen Waschmaschine, mit vertikaler Achse , ist eine Zentrifuge. Um Übertragung der Unwuchten auf die Umgebung (den Aufstellort) zu vermeiden, ist der Motor weich gelagert (mit Gummifedern). Beim Hochlauf einer Wäscheschleuder ergeben sich mehrere Überraschungs-Effekte. Einer davon ist die Synchronisation der Drehzahl mit der Schwingungsfrequenz (das wird weiter oben beim Thema UnwuchtSynchronisation erwähnt). Ein zweiter Effekt bei weichgelagerten Zentrifugen ist ein Kreiseleffekt. Der wird anschließend beschrieben. Experimentelle Anordnung: Ein DC-Motor ist mit (mindestens 3) Federn so gespannt, dass im Ruhezustand die Motorwelle senkrecht steht. Am unteren Ende ist an das Motorgehäuse ein Stütz-Stab koaxiale montiert, dessen unteres Ende als Spitze ausgeführt ist. Diese Spitze stützt sich auf der Grundplatte ab. Das ist ein Schwingungs-System mit 2 Freiheitsgraden. Vor oben gesehen hat man die Auslenkung in x-Richtung und die Auslenkung in y-Richtung. Wegen der Lagerung auf der Spitze ist diese Auslenkung aber keine Translation, sondern eine Drehschwingung um das Spitzenlager. Sensorik: Drehzahlmessung, mit Lichtschranke. Winkelmessung der Drehschwingung um die x-Achse mit einem Biegebalken, von dessen Ende ein Faden gespannt zum Stütz-Stab kurz über dem Spitzenlager. Ein zweiter Biegebalken plus Faden misst die Drehschwingung um die y-Achse. Ohne Rotation der Motorwelle erwartet man zwei Schwingungsformen, eine Drehschwingung um die x-Achse, eine um die y-Achse. Bei symmetrischem Aufbau sind die beiden Eigenfrequenzen für beide Schwingungsformen gleich groß. Obwohl das System zwei Freiheitsgrade hat, findet man also nur eine einzige Frequenz. Man nennt solche Systeme mit gleichen Eigenwerten (Frequenzen), aber verschiedenen Eigenvektoren (Schwigungsformen) auch „entartet“. Diese beiden Schwingungsformen sind entkoppelt, d.h. die Schwingung um die x.Achse beeinflusst die Schwingung um die y-Achse nicht. --- Wäre die Federn unsymmetrisch, dann wären 2 Eigenfrequenzen vorhanden, aber auch dann würden sich die Schwingungen nicht gegenseitig beeinflussen Wenn der auf der Motorwelle ein Schwungrad angebracht ist, dann findet man bei rotierendem Motor einen Überraschungseffekt: Start z.B. so: Winkelauslenkung um die x-Achse und dann loslassen. Dann schwingt die Masse nicht etwa weiter nur um die x-Achse, sondern man erkennt eine seitliche „Ablenkung“. Von oben gesehen ergibt sich für das obere Ende der Motorwelle eine „rosettenfömige“ Schwingungsbahn. Das Spektrum der beiden Sensorsignale zeigt jetzt zwei Frequenzen, eine etwas höher, eine etwas tiefer als die Frequenz ohne Rotation. Die zugehörigen Phasenwinkel sind plus 90 Grad bzw. minus 90 Grad.—Die Frequenzänderung ist umso größer, je größer die Drehzahl ist. Die Drehrichtung der Rosettenbahn hängt von der Drehrichtung des Motors ab. Zur Deutung der beschriebenen Effekte muss man die Kreiselwirkung berücksichtigen. Die rotierende Welle hat einen Drehimpuls pz = wz * Jz (wz = Winkelgeschwindigkeit der Rotation um die Motorachse, Jz = Trägheitsmoment um die Motorachse ). Der Drehimpuls ist ein Vektor, der in Drehrichtung zeigt. Bei der Drehschwingung um das Spitzenlager ändert sich die Richtung der Motorwelle und folglich auch die Richtung des Drehimpulses. Nach dem Drehimpuls-Satz ist der zeitliche Differentialquotient des Drehimpulses gleich dem wirkenden Drehmoment M. Infolge der Drehschwingung entsteht also bei rotierendem Motor ein Drehmoment in Richtung der Änderung des Drehimpulsvektors. Das ergibt im einfachsten Fall (symmetrische Anordnung, keine Reibung) die 4 DGLn: d alfx/dt = wx d alfy/dt = wy J* d wx/dt = (-D*alfx - pz* wy) J* d wy/dt = (-D*alfy + pz* wx) Dabei ist alfx der Drehwinkel um die x-Achse, alfy der Drehwinkel um die y-Achse, wx= Winkelgeschwindigkeit der Drehschwingung um die x-Achse, wy= Winkelgeschwindigkeit der Drehschwingung um die y-Achse, J das Trägheitsmoment der Drehschwingung um das Spitzenlager, D die Federkonstante dieser Drehschwingung, pz = Jz * wz = Drehimpuls um die Motorachse (s.o.). Die numerische Lösung dieses DGL-Systems zeigt die beschriebenen Effekt und ist in guter Übereinstimmung mit den Experimenten. Zusätzlich zum Kreiseleffekt kommt (natürlich ) noch der Effekt der Unwucht-Synchronisation hinzu (s.o). Um den Hochlauf des Motors zu erleichtern, kann man durch Anbringen von Schwingungs-Tilgern die Drehschwingungen dämpfen.. Das Experiment „Zentrifugenlager“ zeigt also gleichzeitig drei Effekte: Kreiselwirkung, Unwucht-Synchronisation, Tilgerwirkung. Prof. Dr. R. Kessler, FH-Karlsaruhe, C:\ro\Si05\didaktik\Laborwagen\Konzepte für Laborwagen3.doc, S. 14/14 Messung der Drehmoment-Kennlinie von Asynchron-Motoren, Messung der Wirbelstromkraft. Bekanntlich haben Asynchron-Drehstrom-Motoren im Vergleich zu Gleichstrom-Motoren eine komplizierte Kennlinie (Drehmoment M als Funktion der Winkelgeschwindigkeit w). Insbesondere ist der Bereich, in dem M mit w ansteigt, ein instabiler Bereich. Folglich kann man diese Kennlinien nicht mit der Methode „Pronyscher Zaum“ messen (Drehmoment-Messung mit Hilfe einer Reib-Bremse an Motorwelle) Alternative Mess-Methode mit Hilfe der Elektronik: Man montiert an den zu testenden Motor eine geeignete Schwungmasse, z. B. eine Kupferscheibe) . Mit einem DC-Tachogenerator wird die Winkelgeschwindigkeit w gemessen . Diese Tachospannung wird zunächst etwas geglättet, z.B. mit einem aktiven Tiefpass 2. Ordnung, und dann differenziert (mit einem OP- Differenzierer ). Mit XY-Schreiber wird in X-Richtung die Winkelgeschwindigkeit w , in Y-Richtung die Ableitung dw/dt dargestellt. Nach Newton ist J*dw/dt = Summe der Drehmomente. (J = Trägheitsmoment der Rotation). Nach Anlegen der Motorspannung wird auf diese Weise die Summe aus Antriebsdrehmoment plus Reibungdrehmoment gemessen. Nach Abschalten der Motorspannung wird der Motor wieder langsamer, dabei misst man das Reibungsdrehmoment allein Statt XY-Schreiber kann man auch ein Digitaloszilloskop verwenden. Die Messwerte in einen PC einziehen und dann die XY-Darstellung z.B. mit Matlab realisieren. Bei dieser experimentellen Anordnung bietet es sich an, die Wirbelstrom-Kraft zu messen: Nach Abstellen der Motorspannung schaltet man ein Magnetfeld ein (z.B. mit Elektromagnet oder einen Dauermagneten mechanisch einschwenken). Das Magnetfeld soll senkrecht zu rotierende Kupferscheibe stehen. Die in der Scheibe induzierten Wirbelströme bewirken infolge des Magnetfeldes eine Bremskraft, die u.a. von der Winkelgeschwindigkeit abhängt. Auch bei diesem Experiment findet man wieder einen Überraschungseffekt: Die Wirbelstromkraft ist keineswegs proportional zur Winkelgeschwindigkeit, sondern mit wachsender Winkelgeschwindigkeit geht die Wirbelstromkraft über ein Maximum und fällt dann wieder ab. Über diese Eigenschaft der Wirbelstromkraft findet man in den Lehrbüchern (Physik, Elektrotechnik) nichts Mit diesem einfachen Experiment erhält man zwei Kennlinien: Beim Hochlauf des Motors die Motorkennlinie (Antriebsdrehmoment als Funktion der Winkelgeschwindigkeit) und beim Auslauf des Motors die Kennlinie einer Wirbelstrombremse (Drehmoment der Wirbelstromkraft als Funktion der Winkelgeschwindigkeit).