Zahlenmengen

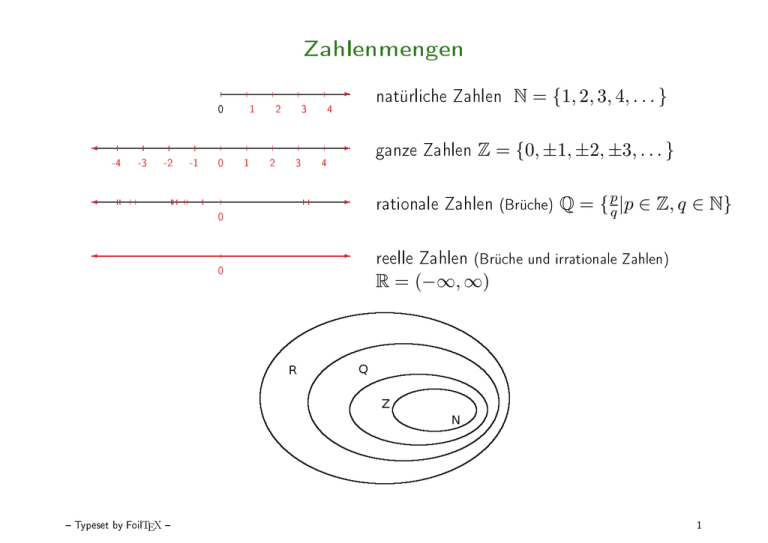
Zahlenmengen
0
1
2
3
-4
-3
-2
-1
0
1
2
3
natürliche Zahlen
-
ganze Zahlen
-
rationale Zahlen (Brüche)
-
reelle Zahlen (Brüche und irrationale Zahlen)
4
4
0
0
Typeset by FoilTEX N = {1, 2, 3, 4, . . . }
-
Z = {0, ±1, ±2, ±3, . . . }
Q = { pq |p ∈ Z, q ∈ N}
R = (−∞, ∞)
1
Dezimalsystem (Basis 10)
Endliche, periodische und unendliche Dezimalzahlen:
1. Rationale Zahlen, die mit einer endlichen Anzahl von Dezimalstellen dargestellt
werden können, heiÿen endliche Dezimalzahlen.
zB:
−
126
1
= −1.26, 1984, = 0.125
100
8
2. Nicht jede rationale Zahlen kann als endliche Dezimalzahl dargestellt werden:
100
11
= 33.333 . . . ,
= 0.1571428571428571428 . . .
3
70
allerdings als periodische Dezimalzahl.
3. Die unendlichen, nicht periodischen Dezimalzahlen sind die irrationalen Zahlen.
√
Typeset by FoilTEX √
2, − 5,
2
Also:
•
Die rationalen Zahlen sind die endlichen und periodischen Dezimalzahlen.
•
Die irrationalen Zahlen sind die unendlichen (nicht period.) Dezimalzahlen.
•
Die reellen Zahlen bestehen aus den rationalen und irrationalen Zahlen.
Typeset by FoilTEX 3
Wurzeln
a
1
2
1
2
1
2
=
√
a
für
a≥0
1 1
2+2
= a1 = a
a a = a
√
√ √
ab =
a b
r
√
a
a
= √
b
b
√
√
√
a + b 6=
a+ b
n-te Wurzeln
1
n
a =
√
n
Wenn
a
Typeset by FoilTEX a
eine positive und
n
eine natürliche Zahl ist, dann ist
eindeutig bestimmte positive Zahl, deren
1 n
n
(a ) = a.
n-te
1
an
die
Potenz a ergibt, dh.
4
Gebrochene Exponenten
Wenn
a
q eine natürliche
√
p
√
q p
q
a = a = ( q a)p.
eine positive,
und
p
eine ganze Zahl ist, dann gilt
Weitere Rechenregeln für Potenzen:
ar+s = ar as
(ar )s = ars
1
a−s =
as
Typeset by FoilTEX 5