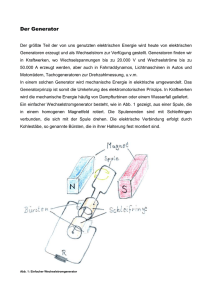
Physik 2 Elektrodynamik und Optik

Physik 2
Elektrodynamik und Optik
Thomas Klinker
Hochschule für Angewandte Wissenschaften Hamburg
2007
Inhaltsverzeichnis
1 Grundlagen der Elektrostatik
1.1 Das COULOMBsche Gesetz . . . . . . . . . . .
1.2 Das elektrische Feld . . . . . . . . . . . . . . . .
1.3 Das elektrische Potential . . . . . . . . . . . . .
1.4 Potential und Feld eines elektrischen Dipols . .
1.5 Das GAUSSsche Gesetz für das elektrische Feld
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Anwendungen der Gesetze der Elektrostatik
2.1 Das elektrische Feld einer ebenen Ladungsverteilung .
2.2 Das elektrische Feld einer linearen Ladungsverteilung
2.3 Das elektrische Feld einer homogen geladenen Kugel .
2.4 Elektrische Felder von Leitern . . . . . . . . . . . . .
2.5 Der FARADAYsche Käfig . . . . . . . . . . . . . . .
2.6 Influenz . . . . . . . . . . . . . . . . . . . . . . . . .
2.7 Kapazität . . . . . . . . . . . . . . . . . . . . . . . .
2.8 Die Energie des elektrischen Feldes . . . . . . . . . .
2.9 Das elektrische Feld in Materie . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Der
3.1
3.2
3.3
3.4
3.5
elektrische Strom
Strom und die Bewegung von Ladungen . . . . . . . . . . .
Elektrische Leitfähigkeit und das OHMsche Gesetz . . . . .
Mikroskopisches Modell für das OHMsche Gesetz . . . . . .
Die elektrische Leistung eines Stromes an einem Widerstand
Die KIRCHHOFFschen Regeln . . . . . . . . . . . . . . . .
4 Das
4.1
4.2
4.3
4.4
magnetische Feld
Kräfte auf bewegte Ladungen im Magnetfeld
Das BIOT-SAVARTsche Gesetz . . . . . . .
Das GAUSSsche Gesetz für das Magnetfeld .
Das AMPEREsche Gesetz . . . . . . . . . .
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
5
8
10
15
19
.
.
.
.
.
.
.
.
.
27
27
28
30
31
35
38
39
46
49
.
.
.
.
.
51
51
53
54
56
58
.
.
.
.
63
63
67
69
72
2
INHALTSVERZEICHNIS
4.5
4.6
4.7
Drehmoment auf eine Leiterschleife im Magnetfeld . . . . . . . . 81
Der HALL-Effekt . . . . . . . . . . . . . . . . . . . . . . . . . . 83
Bahnen freier Ladungen im Magnetfeld . . . . . . . . . . . . . . 85
5 Induktion
5.1 Das FARADAYsche Induktionsgesetz
5.2 Die LENZsche Regel . . . . . . . . .
5.3 Beispiele zum Induktionsgesetz . . .
5.4 Gegeninduktion . . . . . . . . . . . .
5.5 Selbstinduktion . . . . . . . . . . . .
5.6 Der RL-Kreis . . . . . . . . . . . . .
5.7 Die Energie des magnetischen Feldes
5.8 Materie im Magnetfeld . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
89
89
91
93
97
100
104
107
109
6 Elektromagnetische Wellen
6.1 Das AMPERE-MAXWELLsche Gesetz . . . . . . . . . . . .
6.2 Die MAXWELLschen Gleichungen . . . . . . . . . . . . . .
6.3 Grundlagen der Wellenausbreitung . . . . . . . . . . . . . .
6.4 Wellengleichung für das elektrische und magnetische Feld . .
6.5 Energiedichte und Intensität einer elektromagnetischen Welle
.
.
.
.
.
.
.
.
.
.
113
113
115
116
123
130
.
.
.
.
.
.
.
.
.
.
.
133
. 133
. 134
. 136
. 143
. 146
. 155
. 157
. 157
. 158
. 159
. 160
.
.
.
.
163
. 163
. 165
. 170
. 171
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7 Geometrische Optik
7.1 Das HUYGENSsche Prinzip . . . . . . . . . . .
7.2 Prämisse der geometrischen Optik . . . . . . . .
7.3 Reflexion und Brechung . . . . . . . . . . . . .
7.4 Brechung an sphärischen Grenzflächen . . . . .
7.5 Abbildung durch Linsen . . . . . . . . . . . . .
7.6 Das menschliche Auge . . . . . . . . . . . . . .
7.7 Optische Instrumente . . . . . . . . . . . . . . .
7.7.1 Vergrößerung durch optische Instrumente
7.7.2 Lupe . . . . . . . . . . . . . . . . . . . .
7.7.3 Mikroskop . . . . . . . . . . . . . . . . .
7.7.4 Fernrohr . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
8 Beugung
8.1 FRAUNHOFERsche und FRESNELsche Beugung
8.2 Beugung am Spalt . . . . . . . . . . . . . . . . .
8.3 Beugung an einer kreisförmigen Öffnung . . . . .
8.4 Beugung am Gitter . . . . . . . . . . . . . . . . .
A Aufgaben mit Lösungen
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
177
INHALTSVERZEICHNIS
3
B Lineare Differentialgleichungen
199
C Literaturverzeichnis
203
D Physikalische Konstanten
205
E Das Griechische Alphabet
207
4
INHALTSVERZEICHNIS
Kapitel 1
Grundlagen der Elektrostatik
1.1
Das COULOMBsche Gesetz
Durch Reiben eines Plastikstabes an einem Fell oder eines Glasstabes an Seide
kann man Körper elektrisch aufladen. Dabei zeigt sich, dass sich die aufgeladenen Gegenstände entweder anziehen oder abstoßen. Die Erklärung ist, dass
alle Materie zwei Arten von Ladung besitzt, positive und negative. Ungeladene
Körper haben gleich viel positive wie negative Ladung. Durch Reiben kann nun
Ladung von einem Körper auf einen anderen übergehen. Ist dieser Aufladungsvorgang beendet, hat der eine Körper einen Überschuss an positiver Ladung,
der andere einen Überschuss an negativer Ladung. Weiter zeigt sich, dass sich
Objekte mit gleicher Ladung abstoßen, während sich Objekte mit ungleicher
Ladung anziehen. Reibt man einen Glasstab an Seide, so gibt er beispielsweise
Elektronen an die Seide ab. Träger der Ladung sind die Protonen und Elektronen der Atome. Es zeigt sich weiter, dass die Ladung quantisiert ist, d.h.
Ladung tritt in der Natur nur als ganzzahliges Vielfaches einer Elementarladung auf. Diese Elementarladung konnte zum ersten Mal 1909 von MILLIKAN
mit seinem berühmten Öltröpfchenversuch bestimmt werden. Sie hat den Wert
e = 1, 602 · 10−19 C .
(1.1)
Das Coulomb (C) ist hierbei die Einheit der Ladung, auf die wir weiter unten
zu sprechen kommen. Ein weiteres fundamentales Gesetz ist das Gesetz der
Ladungserhaltung: In einem abgeschlossenen System bleibt die Gesamtladung
erhalten, egal welche Vorgänge in diesem System im Detail ablaufen.
Die Kraft zwischen ruhenden elektrischen Ladungen wurde von COULOMB
untersucht, und er fand ein Gesetz ähnlich dem NEWTONschen Gravitationsgesetzt. Es lautet:
5
6
1 Grundlagen der Elektrostatik
Eine Ladung q1 übt auf eine Ladung q0 eine Kraft aus, die dem
Produkt aus beiden Ladungen proportional und dem Quadrat des
Abstandes beider Ladungen umgekehrt proportional ist. Die Kraft
wirkt in Richtung der Verbindungslinie zwischen beiden Ladungen,
in Zeichen
q0 q1
F~ = k 2 ~ˆr01 .
(1.2)
r01
Hierbei ist ~r01 der Vektor, der vom Ort der Ladung q1 zum Ort
der Ladung q0 zeigt, ~ˆr01 der zugehörige Einheitsvektor und r01 der
Abstand beider Ladungen.
Der Wert der Proportionalitätskonstanten k hängt von dem verwendeten Einheitensystem ab. Im SI-Einheitensystem setzt man die Proportionalitätskonstante k zu
1
k=
,
(1.3)
4πε0
wobei die elektrische Feldkonstante ε0 den Wert
ε0 = 8, 854 · 10−12 C2 m−2 N−1
(1.4)
erhält. Damit hat k den Wert
k=
1
= 8, 9876 · 109 N m2 C−2 .
4πε0
(1.5)
Hierbei steht C für die Einheit der Ladung, das Coulomb. Der exakte Wert
von ε0 kann erst später genau begründet werden. Er ergibt sich dadurch, das
die Einheit der Ladung nicht durch Gl. (1.2) festgelegt wird, sondern an die
Definition der Einheit der Stromstärke, das Ampere (A), geknüpft ist, siehe
Kap. 4.1. Mit der in Kap. 6.4 hergeleiteten Gleichung
c= √
1
,
ε0 µ0
wobei µ0 die magnetische Feldkonstante und c die Lichtgeschwindigkeit im
Vakuum ist, ergibt sich obiger Wert für ε0 . Wir wollen dies hier nicht weiter
verfolgen, sondern verweisen auf die entsprechenden späteren Kapitel. Aus
Gl. (1.2) läßt sich aber ablesen, das für die Ladungseinheit Coulomb gilt:
Ein Coulomb ist diejenige Ladung, die eine gleichgroße Ladung in
einem Abstand von 1 m mit einer Kraft von etwa 9 · 109 N abstößt.
1.1 Das COULOMBsche Gesetz
7
Wirken auf eine Ladung q0 mehrere Ladungen qi (i = 1, . . . , n), so zeigt
die experimentelle Beobachtung, dass sich die Gesamtkraft auf die Ladung
q einfach durch Addition der einzelnen Kräfte gemäß dem COULOMBschen
Gesetz (1.2) ergibt, in Zeichen
F~ =
n
1 X
q0 qi ˆ
~r0i .
2
4πε0 i=1 r0i
(1.6)
Hierbei ist ~r0i der Vektor, der vom Ort der Ladung qi zum Ort der Ladung q0
zeigt, ~ˆr0i der zugehörige Einheitsvektor und r0i der Abstand beider Ladungen.
Diese Gleichung kann auch in der folgenden Form geschrieben werden:
F~ =
n
q0 qi ~r − ~ri
1 X
.
4πε0 i=1 |~r − ~ri |2 |~r − ~ri |
(1.7)
Hierbei bezeichnet ~r den Ort der Ladung q0 und ~ri den Ort, an dem sich die
Ladung qi befindet, siehe Abb. 1.1. ~r0i = ~r − ~ri ist der Vektor, der vom Ort
~ri der Ladung qi zum Ort ~r der Ladung q0 zeigt. ~ˆr0i = (~r − ~ri )/|~r − ~ri | ist der
zugehörige Einheitsvektor und |~r − ~ri | der Abstand, den die Ladungenq0 und
qi voneinander haben. Die in Gl. (1.7) beschriebene vektorielle Addition der
Einzelkräfte zur Gesamtkraft wird auch als Superpositionsprinzip bezeichnet.
Abbildung 1.1: Kraft auf eine Ladung q0 am Ort ~r verursacht von mehreren
Punktladung qi an den Orten ~ri (i = 1, . . . , n).
8
1.2
1 Grundlagen der Elektrostatik
Das elektrische Feld
~ einer Ladungsverteilung an einem Ort ~r wird definiert
Das elektrische Feld E
als die Kraft, die diese Ladungsverteilung auf eine Probeladung q0 am Orte ~r
bewirkt, dividiert durch den Wert dieser Probeladung, in Zeichen
~
~ := F .
E
q0
(1.8)
Damit lässt sich die Kraft auf die Probeladung q0 schreiben in der Form
~ .
F~ = q0 E
(1.9)
Die im COULOMBschen Gesetz beschriebene Fernwirkung der elektrostatischen Kraft auf eine Ladung wird auf diese Weise gedeutet als lokale Wechselwirkung dieser Ladung mit einem von den übrigen Ladungen erzeugten Feld.
Diese Idee geht auf FARADAY zurück. Aus der Definitionsgleichung des elek~
trischen Felds Gl. (1.8) und Gl. (1.7) folgt direkt für das elektrische Feld E
am Orte ~r, bewirkt von n Punktladungen qi (i = 1, . . . , n), die sich an den
Raumpunkten ~ri befindet:
~ r) =
E(~
n
1 X
~r − ~ri
qi
.
4πε0 i=1 |~r − ~ri |2 |~r − ~ri |
(1.10)
Für das elektrische Feld einer einzigen Punktladung q, die sich im Koordinatenursprung befindet, ergibt sich insbesondere
~ r) =
E(~
1 q ˆ
~r .
4πε0 r2
(1.11)
Hierbei ist ~ˆr der Einheitsvektor in Richtung von ~r. Gl. (1.11) werden wir im
folgenden noch sehr oft verwenden.
Ist die Ladungsverteilung nicht punktförmig, sondern kontinuierlich, so muss
sie durch eine Dichtefunktion ̺(~r ) beschrieben werden. Die Funktion ̺(~r ) gibt
dabei die Ladungsdichte an der Stelle ~r an. Sie ist definiert durch
∆Q
.
∆V →0 ∆V
̺(~r ) = lim
(1.12)
Hierbei ist ∆Q die Ladung eines Volumens ∆V , welches sich bei der Grenzwertbildung in Gl. (1.12) auf den Raumpunkt ~r zusammenzieht. Die Einheit
der Ladungsdichte ̺ ergibt sich zu C/m3 . Um das elektrische Feld einer kontinuierlichen Ladungsverteilung zu berechnen, teilt man das Gesamtvolumen
9
1.2 Das elektrische Feld
Abbildung 1.2: Zur Berechnung des elektrischen Feldes einer kontinuierlichen
Ladungsverteilung.
V , über das sich die Ladung erstreckt, in kleine Volumenelemente ∆Vi mit
i = 1, . . . , n. Sind die Volumenelemente ∆Vi hinreichend klein, so kann die Ladungsdichte über jedem Volumenelement ∆Vi als konstant angesehen werden
mit dem Wert ̺(~ri ), wobei ~ri der Ortsvektor zu einem beliebigen Punkt des
Volumenelementes ∆Vi ist. Das Volumenelementes ∆Vi trägt damit die Ladung ∆Qi = ̺(~ri ) ∆Vi . Das elektrische Feld der gesamten Ladungsverteilung
ergibt sich dann mit Gl. (1.10) zu
~ r ) = lim
E(~
∆Vi →0
n
1 X
̺(~ri ) ~r − ~ri
∆Vi .
4πε0 i=1 |~r − ~ri |2 |~r − ~ri |
(1.13)
Bei obiger Grenzwertbildung streben alle Volumenelemente ∆Vi gegen 0 und
ihre Gesamtzahl n damit gegen ∞. Der Grenzwert in Gl. (1.13) wird als Volumenintegral bezeichnet und geschrieben in der Form:
~ r) =
E(~
1 Z ̺(~r ′ ) ~r − ~r ′
dV ′ .
′
2
′
4πε0
|~r − ~r | |~r − ~r |
(1.14)
V
dV ′ ist hierbei das differentielle Volumenelement (siehe Abb. 1.2), welches bei
Verwendung kartesischerkoordinaten die Form hat dV ′ = dx′ dy ′ dz ′ . Mit den
Gln. (1.10) und (1.14) kann im Prinzip das elektrische Feld jeder Ladungsverteilung berechnet werden. Allerdings bringt die Auswertung des Volumenintegrals in Gl. (1.14) manchmal erhebliche mathematische Probleme mit sich.
Wir verfolgen dies deshalb hier nicht weiter, weil wir später auch noch andere
Methoden kennenlernen werden, elektrische Felder zu berechnen.
10
1.3
1 Grundlagen der Elektrostatik
Das elektrische Potential
In der Mechanik wird die potentielle Energie Ep eines Teilchen in einem konservativen Kraftfeld F~ eingeführt durch
Ep (~r) = −
Z~r
F~ d~r .
(1.15)
~
r0
Die potentielle Energie entspricht der Arbeit, die für eine Verschiebung des
Teilchens vom Punkte ~r0 zum Punkte ~r gegen das Kraftfeld F~ verrichtet werden
muß. Sie kann interpretiert werden als Lageenergie, welche das Teilchen im
Punke ~r besitzt. ~r0 ist der Bezugspunkt der potentiellen Energie. In ~r0 gilt
Ep (~r0 ) = 0. Wir betrachten nun eine Probeladung q0 in einem elektrischen
~ Sie erfährt die Kraft F~ = q0 E
~ und hat damit gemäß Gl. (1.15) die
Feld E.
potentielle Energie
Ep (~r) = − q0
Z~r
~ d~r .
E
(1.16)
~
r0
Das elektrische Potential ist nun einfach definiert als die potentielle Energie
pro Ladungseinheit, in Zeichen
~
r
Z
Ep (~r)
~ d~r .
ϕ(~r) =
=− E
q0
(1.17)
~
r0
Die Einheit des elektrischen Potentials ϕ wird als Volt (V) festgesetzt, wobei
gemäß Gl. (1.17) gilt V = J/C. Für die Einheit des elektrischen Feldes E ergibt
sich damit V/m.
Damit die Definition (1.17) sinnvoll ist, muss das dort auftretende Kurvenintegral wegunabhängig sein. Das ist aber genau dann der Fall, wenn für jede
beliebige geschlossene Kurve C gilt:
I
~ d~r = 0 .
E
(1.18)
C
Wir werden im folgenden nachweisen, dass dieser Sachverhalt für statische
elektrische Felder gilt. Wir betrachten dazu zunächst das elektrische Feld einer
Punktladung,
~ = 1 q ~ˆr .
E
(1.19)
4πε0 r2
Wir betrachten außerdem zunächst eine spezielle geschlossene Kurve, wie sie
in Abb. 1.3 dargestellt ist. Sie besteht aus den zwei konzentrischen Kreisbögen
11
1.3 Das elektrische Potential
Abbildung 1.3: Eine spezielle geschlossene Kurve im Feld einer Punktladung
bestehend aus zwei konzentrischen Kreisbögen C1 und C2 , die verbunden sind
durch zwei geradlinige, radial verlaufende, Wegstücke C3 und C4 . Die gesamte
Kurve werde im Gegenuhrzeigersinn durchlaufen.
C1 mit dem Radius r1 und C2 mit dem Radius r2 , die verbunden sind durch
die geradlinigen radial verlaufenden, Wegstücke C3 und C4 . Die gesamte Kurve
werde im Gegenuhrzeigersinn durchlaufen. Die Wegintegrale längs der Kreis~ in jedem
bogensegmente C1 und C2 verschwinden, da das elektrische Feld E
Punkt dieser Kurvenstücke senkrecht auf d~r steht, also
Z
~ d~r =
E
C1
Z
~ d~r = 0 .
E
C2
Für die radial verlaufenden geradlinigen Wegstücke gilt:
Z
~ d~r =
E
Z
~ d~r =
E
C3
bzw.
C4
also:
Zr2
r1
r2
q Z 1
1
q
1
E dr =
,
dr =
−
4πε0 r r2
4πε0 r1 r2
Zr1
r1
q Z 1
1
q
1
E dr =
,
dr =
−
4πε0 r r2
4πε0 r2 r1
r2
1
2
Z
C4
~ d~r = −
E
Z
C3
~ d~r .
E
12
1 Grundlagen der Elektrostatik
Damit gilt für die geschlossene Kurve in Abb. 1.3:
I
~ d~r = 0 .
E
(1.20)
C
Dieser Sachverhalt lässt sich nun direkt auf beliebiege geschlossene Kurven
verallgemeinern. Wie in Abb. 1.4 dargestellt, kann eine beliebige geschlossene Kurve C beliebig genau approximiert werden durch kleine konzentrische
Kreisbögen, die durch kleine radial verlaufende, geradlinige Wegstücke verbunden sind. Die Anteile zum Kurvenintegral entlang der Kreisbögen verschwin-
Abbildung 1.4: Eine beliebige geschlossene Kurve im Feld einer Punktladung.
~ senkrecht auf diesen Wegstücken steht.
den wieder, da das elektrische Feld E
Die Anteile entlang der geradlinigen Wegstücke, z.B. entlang C1 und C2 in
Abb. 1.4, heben sich paarweise auf, ganz ähnlich wie bei der in Abb. 1.3 dargestellten Konfiguration. Damit gilt die Beziehung in Gl. (1.20) für beliebige
geschlossenen Kurven im Feld einer Punktladung. Auf Grund des Prinzips der
Superposition und wegen der Linearität des Integrals gilt die Beziehung schließlich aber auch für beliebige Ladungsverteilungen. Zusammenfassend haben wir
damit folgenden Sachverhalt bewiesen:
Das Integral des elektrostatischen Feldes längs einer beliebigen geschlossenen Kurve C ist Null, in Zeichen:
I
~ d~r = 0 .
E
(1.21)
C
Man kann dies auch so formulieren: Das elektrostatische Feld ist
wirbelfrei“.
”
13
1.3 Das elektrische Potential
Damit ist aber auch die Definition des elektrischen Potentials in Gl. (1.17)
sinnvoll. Aus dieser Definition ergibt sich direkt, dass die Flächen gleichen Potentials, die sogenannten Äquipotentialflächen stets senkrecht zum elektrischen
~ verlaufen. Es sei noch ausdrücklich darauf hingewiesen, dass Gl. (1.21)
Feld E
nur für statische elektrische Felder gilt, nicht aber, wie wir später sehen werden,
für zeitabhängige elektromagnetische Felder.
Wir wollen nun das elektrische Potential einiger konkreter Ladungsverteilungen berechen. Wir bestimmen zunächst das Potential einer Punktladung q,
welche sich im Ursprung des Koordinatensystems befindet. Aus Symmetriegründen hängt das Potential nur vom Abstand r vom Zentrum ab. Wegen der
Wegunabhängigkeit des Integrals in Gl. (1.17) können wir einen radial verlaufenden, geradlinigen Weg wählen. Als Bezugspunkt werde das Unendliche,
r0 = ∞, gewählt. Mit Gl. (1.17) und (1.19) folgt
ϕ(r) = −
Zr
∞
E dr =
Z∞
r
∞
q Z 1
q 1
E dr =
dr =
.
2
4πε0 r r
4πε0 r
Das elektrische Potential einer Punktladung q lautet somit:
ϕ(r) =
1 q
.
4πε0 r
(1.22)
Wird das elektrische Feld von mehreren Punktladungen qi (i = 1, . . . , n) hervorgerufen, wobei sich die Ladung qi am Ort ~ri befinde, so folgt aus dem Superpositionsprinzip und der Linearität des Integrals für das elektrische Potential
am Ort ~r
n
qi
1 X
.
(1.23)
ϕ(~r) =
4πε0 i=1 |~r − ~ri |
Dabei ist |~r − ~ri | der Abstand des betrachteten Punktes ~r vom Ort ~ri der i-ten
Punktladung. Liegt schließlich eine kontinuierliche Ladungsverteilung mit der
Ladungsdichte ̺(~r ′ ) vor, so erhält man für das elektrische Potential
1 Z ̺(~r ′ )
ϕ(~r) =
dV ′ .
4πε0
|~r − ~r ′ |
(1.24)
V
Die Potentiale weiterer Ladungsverteilungen werden wir in Kap. 2 im Zusammenhang mit Kondensatoren berechen.
Die Potentialdifferenz zwischen zwei Punkten ~r1 und ~r2 in einem elektrischen
Feld hat große praktische Bedeutung. Sie wird als elektrische Spannung U
bezeichnet. Sie gibt die Arbeit an, die notwendig ist, eine Einheitsladung in
14
1 Grundlagen der Elektrostatik
~ von ~r1 nach ~r2 zu bewegen. Aus Gl. (1.17) folgt direkt
dem elektrischen Feld E
U = ϕ(~r2 ) − ϕ(~r1 ) = −
Z~r2
~ d~r .
E
(1.25)
~
r1
Die Spannung U wird natürlich wie das Potential ϕ in Volt (V) gemessen. Da in
praktischen Anwendungen immer nur Potentialdifferenzen eine Rolle spielen,
ist man bei der Wahl des Bezugspunktes ~r0 in Gl. (1.17) frei. Die Festlegung,
das Potential einer Punktladung im Unendlichen (r0 = ∞) auf den Wert Null
zu setzen, ist bequem, aber willkürlich und keinesfalls notwendig.
Die Gleichung
ϕ(~r) = −
Z~r
~ d~r .
E
(1.26)
~
r0
liefert den Zusammenhang zwischen dem Potential ϕ und dem elektrischen Feld
~ in Form eines Integrals. Man kann mit Gl. (1.26) bei bekanntem Feldverlauf
E
das zugehörige Potential berechnen. Man kann aus Gl. (1.26) aber auch einen
differentiellen Zusammenhang zwischen dem Feld und dem Potential herleiten.
Dieser ermöglicht die Berechnung des elektrischen Feldes, wenn das elektrische
Potential bekannt ist. Dies ist in der Praxis hilfreich, da das Potential einer
Ladungsverteilung manchmal einfacher zu berechenen ist als das elektrische
Feld. Wir betrachten dazu die Potentialdifferenz dϕ = ϕ(~r + d~r) − ϕ(~r) zweier
benachbarter Punkte ~r = (x, y, z) und ~r + d~r = (x + dx, y + dy, z + dz). Die
Änderung des Potentials, wenn man vom ersten zum zweiten Punkt übergeht,
ist gegeben durch
∂ϕ
∂ϕ
∂ϕ
dϕ =
dx +
dy +
dz .
(1.27)
∂x
∂y
∂z
∂ϕ/∂x, ∂ϕ/∂y und ∂ϕ/∂z sind die partiellen Ableitungen der Funktion ϕ. Die
partielle Ableitung ∂ϕ/∂x beschreibt dabei die Änderung von ϕ in x-Richtung,
wobei die übrigen Variablen y und z konstant gehalten werden. Den Ausdruck
in Gl. (1.27) bezeichnet man auch als totales Differential. Aus Gl. (1.26) ergibt
sich andererseits für dϕ
~ d~r = − (Ex dx + Ey dy + Ez dz) ,
dϕ = − E
(1.28)
~ = (Ex , Ey , Ez ). Durch Vergleich von Gl. (1.27) und (1.28) folgt
mit E
Ex = −
∂ϕ
,
∂x
Ey = −
∂ϕ
,
∂y
Ez = −
∂ϕ
,
∂z
(1.29)
15
1.4 Potential und Feld eines elektrischen Dipols
oder
~ = − ∂ϕ , ∂ϕ , ∂ϕ
E
∂x ∂y ∂z
!
,
(1.30)
oder
~ = − grad ϕ ,
E
(1.31)
wobei der Gradient einer Funktion definiert ist durch
grad ϕ =
∂ϕ ∂ϕ ∂ϕ
,
,
∂x ∂y ∂z
!
.
(1.32)
Der Gradient einer Funktion zeigt allgemein in Richtung des stärksten Anstiegs, und er steht senkrecht auf den Flächen, auf denen die Funktion konstant
ist. Das elektrische Feld zeigt demzufolge in Richtung der stärksten Abnahme des Potentials und steht senkrecht auf den Äquipotentialflächen, was uns
bereits bekannt ist.
1.4
Potential und Feld eines elektrischen Dipols
In diesem Abschnitt wollen wir das Potential und das Feld eines elektrischen
Dipols berechenen. Ein elektrischer Dipol besteht aus zwei Punktladungen +q
und −q, die in einem Abstand d voneinander angeordnet sind, siehe Abb. 1.5.
Der Dipol sei ohne Beschränkung der Allgemeinheit parallel zur z-Achse angeordnet. Die Ladung +q befindet sich am Ort ~r+ = (0, 0, d/2) und die Ladung
−q am Ort ~r− = (0, 0, −d/2). Der Koordinatenursprung liegt somit in der Mitte zwischen beiden Ladungen. Das elektrische Potential ϕ(x, y, z) eines solchen
Dipols im Raumpunkt ~r = (x, y, z) ergibt sich gemäß Gl. (1.17) zu:


1 
q
−q
 .
q
ϕ(x, y, z) =
+q
4πε0
x2 + y 2 + (z − d2 )2
x2 + y 2 + (z + d2 )2
(1.33)
Häufig
man sich für das Potential in einem großen Abstand
√ 2interessiert
2
2
r = x + y + z vom Dipol, d.h. d ≪ r bzw. d/r ≪ 1. In diesem Fall gilt
die Näherung
d2
x +y +z −zd+
4
2
2
2
!− 1
2
= r
2
d2
zd
1− 2 + 2
r
4r
!!− 1
2
zd
1
1+ 2
≈
r
2r
!
.
16
1 Grundlagen der Elektrostatik
Abbildung 1.5: Zur Berechnung des Potentials eines elektrischen Dipols im
Punkte ~r = (x, y, z). Eingezeichnet sind auch die Polarkoordinaten r und θ.
Hierbei haben wir zunächst den Term d2 /4r2 vernachlässigt, da er quadratisch in d/r ist, und somit gilt d2 /4r2 ≪ zd/r2 . Schließlich haben wir noch die
Beziehung (1 + x)−1/2 ≈ 1 − x/2 für |x| ≪ 1 ausgenutzt. Analog gilt
d2
x2 + y 2 + z 2 + z d +
4
!− 1
2
1
zd
≈
1− 2
r
2r
!
.
Mit Gl. (1.33) folgt für das Potential des Dipols im Fernfeld (r ≫ d):
ϕ(x, y, z) =
1 (q d) z
.
4πε0 r3
(1.34)
Wir führen nun das Dipolmoment p~ ein gemäß
p~ = q d~ ,
wobei d~ = ~r+ − ~r− = (0, 0, d) der Abstandsvektor ist, der von der negativen
zur positiven Ladung zeigt. Führen wir noch, wie in Abb. 1.5 dargestellt, θ als
Winkel zwischen den Vektoren p~ und ~r ein, so gilt z/r = cos θ. Damit erhalten
17
1.4 Potential und Feld eines elektrischen Dipols
wir aus Gl. (1.34) das Potential eines Dipols in folgender Form, die unabhängig
von der speziellen Lage des Dipols im Koordinatensystem ist:
ϕ(~r) =
1 p~ ~r
1 p cos θ
=
.
2
4πε0 r
4πε0 r3
(1.35)
Für die weitere Berechnung sei der Dipol der Einfachheit halber wieder parallel
zur z-Achse orientiert, also p~ = (0, 0, p) mit p = q d, womit sich das Potential
ergibt zu
1 pz
ϕ(x, y, z) =
.
(1.36)
4πε0 r3
~ des Dipols erhält man gemäß Gl. (1.29) durch GradiDas elektrische Feld E
entenbildung aus dem elektrischen Potential, Gl. (1.33), bzw. im Fernfeld aus
Gl. (1.36). Wir beschränken uns auf die Berechnung des elektrischen Feldes im
Fernfeld und erhalten aus Gl. (1.36)
∂ϕ
p ∂ϕ
Ex = −
= −
∂x
4πε0 ∂x
∂ϕ
p ∂ϕ
Ey = −
= −
∂y
4πε0 ∂y
p ∂ϕ
∂ϕ
= −
Ez = −
∂z
4πε0 ∂z
3
2
!
=
p 3zx
,
4πε0 r5
3
2
!
=
p 3zy
,
4πε0 r5
!
−p
=
4πε0
z
(x2 + y 2 + z 2 )
z
(x2 + y 2 + z 2 )
z
3
(x2 + y 2 + z 2 ) 2
1
3 z2
−
r3
r5
!
p 3 cos2 θ − 1
=
.
4πε0
r3
Da das Feld rotationssymmetrisch um die Dipolachse (z-Achse) ist, ist es sinn~ in zwei Komponenten zu zerlegen, von denen die
voll das elektrische Feld E
~ k ) parallel zur Dipolachse und die andere (E
~ ⊥ ) senkrecht dazu steht.
eine (E
Aus den obigen Beziehungen folgt
E⊥ =
q
Ex2 + Ey2 =
p 3z q 2
p 3 cos θ sin θ
x + y2 =
, (1.37)
5
4πε0 r
4πε0
r3
p 3 cos2 θ − 1
,
(1.38)
4πε0
r3
√
wobei wir die Beziehung x2 + y 2 /r = sin θ benutzt haben, welche man direkt
aus Abb. 1.5 ablesen kann. Der Verlauf des Potentials und des Feldes eines
elektrischen Dipols ist in Abb. 1.6 dargesellt. Der Verlauf des Feldes im Fernfeld
wird durch die Gln. (1.37) und (1.38) wiedergegeben. Insbesondere zeigt sich,
Ek = Ez =
18
1 Grundlagen der Elektrostatik
~ ⊥ ) verschwindet für θ = 00 und θ = 900 . Die parallele Feldkomponenete
dass (E
~ k ) hat für θ = 00 den Wert
(E
~k =
E
p
2πε0 r3
für θ = 00 ,
(1.39)
−p
4πε0 r3
für θ = 900 .
(1.40)
und für θ = 900 den Wert
~k =
E
Sie ist damit bei gleichem Abstand r für θ = 00 doppelt so groß wie für θ = 900
und sie ist umgekehrt gerichtet. Die Gln. (1.37) und (1.38) zeigen außerdem,
dass das Feld des elektrische Dipols in alle Richtungen proportional zu 1/r3
nach außen abfällt.
Abbildung 1.6: Die Äquipotentialflächen (gestrichelt) und die Feldlinien eines
elektrischen Dipols.
1.5. DAS GAUSSSCHE GESETZ FÜR DAS ELEKTRISCHE FELD
1.5
19
Das GAUSSsche Gesetz für das elektrische Feld
Wir wollen in diesem Kapitel einen Zusammenhang zwischen dem elektrischen
Feld und seinen Quellen, den elektrischen Ladungen herleiten. Zur Formulierung des GAUSSschen Gesetzes müssen wir zunächst den Begriff des Flusses eines Vektorfeldes erläutern. Für die strömenden Teilchen eines Gases oder einer
Flüssigkeit hat der Fluss eine ganz anschauliche Bedeutung, die wir zunächst
betrachten. In Abb. 1.7 ist eine kleine Fläche A gezeigt, durch die Teilchen mit
der Geschwindigkeit ~v strömen. Die Geschwindigkeit ~v sei über dem ganzen
Bereich der Fläche A konstant. Weiter sei ̺ die Zahl der Teilchen pro Volumeneinheit. Steht die Fläche A senkrecht auf dem Vektorfeld ~v , so ist der
Teilchenfluss durch die Fläche A gegeben durch Φ = ̺ v A, liegt die Fläche parallel im Teichenstrom, so verschwindet der Fluss, Φ = 0. Im allgemeinen Fall
schließlich, die Flächennormle ~n bildet dann den Winkel θ mit dem Vektorfeld
~v , ist der Fluss durch die Fläche A gegeben durch
Φ = ̺ v A cos θ .
(1.41)
~ = ~n A und die Teilchenstromdichte ~j = ̺ ~v
Führt man den Flächenvektor A
ein, so kann man den Fluss in Gl. (1.41) auch schreiben in der Form
~ .
Φ = ~j A
Ist der Teilchenfluss inhomogen oder die Fläche A gekrümmt oder beides,
~ i = ~ni ∆Ai
so muss man die Fläche A in viele kleine Flächenelemente ∆A
unterteilen, durch die dann jeweils der Teilchenstrom ~ji tritt. Der Gesamtfluss
des Teichenstroms durch die Fläche A ist dann gegeben durch
Φ = lim
∆Ai →0
n
X
~i ,
~ji ∆A
i=1
Abbildung 1.7: Der Teilchenfluss Φ durch eine Fläche A bei unterschiedlicher
Orientierung der Fläche.
20
1 Grundlagen der Elektrostatik
oder
Φ=
Z
~ ,
~j dA
(1.42)
A
wobei Gl. (1.42) das Flächenintegral des Teilchenflusses ~j über die Fläche A
darstellt. Es liefert hier die Zahl der Teilchen, die pro Sekunde durch die betrachtete Fläche treten.
Wir wollen nun diese Definition des Flusses, die für beliebige Vektorfelder
~ anwenden. Dann ergibt sich der Fluss des
gilt, auf das elektrische Feld E
elektrischen Feldes durch eine Fläche A zu
Φ=
Z
~ dA
~ .
E
(1.43)
A
Nach diesen Vorbetrachtungen können wir nun das GAUSSsche Gesetz für für
das elektrische Feld formulieren:
~ durch eine geschlossene OberDer Fluss des elektrischen Feldes E
fläche A ist gleich der gesamten Ladung Q, die sich innerhalb dieser
Fläche befindet, dividiert durch ε0 , in Zeichen:
I
A
~ dA
~= Q .
E
ε0
(1.44)
Obige Aussage kann man auch so formulieren: Ladungen sind die Quellen und
Senken des elektrischen Feldes. Die elektischen Feldlinien beginnen demzufolge
bei den positiven Ladungen und enden bei den negativen.
Im Folgenden wollen wir zeigen, dass das GAUSSsche Gesetz (1.44) aus
dem COULOMBschen Gesetz hergeleitet werden kann. Wir betrachten dazu
zunächst das elektrische Feld einer Punktladung q (wobei wir q > 0 voraussetzen), welche sich im Ursprung des Koordinatensystems befindet. Nach dem
COULOMBschen Gesetz ist das Feld gegeben durch
~ =
E
1 q ˆ
~r .
4πε0 r2
Wir betrachten nun den Fluss des elektrischen Feldes durch ein Kugelsegment,
welches sich außerhalb der Ladung q befindet, siehe Abb. 1.8. Das Kugelsegment wird innen und außen berandet durch die Flächen A1 und A2 , die jeweils
Ausschnitte aus einer Kugeloberfläche sind mit dem Radius r1 bzw. r2 , und
die an den Ecken begrenzt werden durch vier radial vom Ursprung nach außen
laufende Strahlen. Die Flächenvektoren sind alle, wie stets bei geschlossenen
21
1.5 Das GAUSSsche Gesetz für das elektrische Feld
Abbildung 1.8: Der Fluss des elektrischen Feldes einer Punktladung q durch
ein Kugelsegment, welches sich außerhalb der Ladung befindet.
Oberflächen, nach außen gerichtet. Der Fluß durch die vier planaren Seitenflächen, die durch die radial nach außen verlaufenden Geraden berandet werden, ist Null, da das elektrische Feld tangential in diesen Flächen liegt, bzw.
~ steht. Der Fluss durch die Fläche A2
die Flächennormale dort senkrecht auf E
~
~
ist positiv, da die Richtung von E parallel ist zu der des Flächenvektors dA.
Da das elektrische Feld in jedem Punkt der Fläche A2 den konstanten Betrag
E2 = q/4πε0 r22 hat, berechnet sich der Fluss durch das Flächenstück A2 zu
Z
A2
~ dA
~ = E2 A2 =
E
q
A2 .
4πε0 r22
Ganz ähnlich erhält man den Fluss durch die Fläche A1 , wobei der Fluss hier
~ hier entgegengesetzt ist zu der von dA.
~
negativ ist, da die Richtung von E
Da das elektrische Feld in jedem Punkt der Fläche A1 den konstanten Betrag
E1 = q/4πε0 r12 hat, ergibt sich der Fluss durch das Flächenstück A1 zu
Z
A1
~ dA
~ = − E1 A1 = −
E
q
A1 .
4πε0 r12
Da die beiden sphärischen Flächenelemente A1 und A2 durch die selben radial nach außen verlaufenden Strahlen begrenzt sind, gilt A2 /A1 = r22 /r12 oder
A2 = (r22 /r12 ) A1 . Für den Fluss durch die Fläche A2 erhält man damit
Z
A2
~ dA
~=
E
Z
q
r22
q
~ dA
~ .
E
A
=
A
=
−
1
1
4πε0 r22 r12
4πε0 r12
A1
(1.45)
22
1 Grundlagen der Elektrostatik
Abbildung 1.9: Der Fluss des elektrischen Feldes einer Punktladung q durch
eine beliebige geschlossenen Fläche, welche die Ladung nicht umschließt.
Der Fluss durch die Fläche A2 ist also genau entgegengesetzt gleich groß dem
Fluß durch die Fläche A1 . Damit ist der gesamten Fluss des elektrischen Feldes
durch die geschlossene Oberfläche des in Abb. 1.8 dargestellten Kugelsegmentes gleich Null. Dieser Sachverhalt lässt sich nun direkt verallgemeinern auf
beliebige geschlossene Flächen, welche die Ladung q nicht umschliessen. Eine
beliebige Fläche kann, wie in Abb. 1.9 dargestellt wird, beliebig genau durch
eine immer feiner werdende Überlagerung von geeigeten Kugelsegmenten aufgebaut werden. Die geschlossene Fäche wird dabei angenähert durch sphärische Flächenstücke, die miteinander verbunden sind durch radial nach außen
verlaufende, planare Flächenstücke. In Abb. 1.9 ist dies in Form eines Schnittbildes dargestellt. Der Fluss durch die planaren Flächenstücke verschwindet,
da die elektrische Feldstärke tangential in diesen Flächenstücken liegt. Der
Fluss durch die sphärischen Flächenstücke, z.B. durch die Flächenstücke A1
und A2 in Abb. 1.9, hebt sich paarweise auf, wie wir weiter oben an Hand der
in Abb. 1.8 dargestellten Konfiguration ausführlich begründet hatten. Damit
ist aber der Fluß durch die gesamte geschlossene Fläche gleich Null. Wir haben somit gezeigt, dass der Fluss des elektrischen Feldes einer Punktladung
durch eine beliebige geschlossene Fläche, welche die Ladung nicht umschließt,
verschwindet.
Als nächstes berechnen wir den Fluss des elektrischen Feldes einer Punktladung q durch eine Kugeloberfläche, in deren Zentrum sich die Ladung befindet.
~ in
Der Radius der Kugel sei r. Der Fluss ist positiv, da die Richtung von E
1.5 Das GAUSSsche Gesetz für das elektrische Feld
23
Abbildung 1.10: Der Fluss des elektrischen Feldes einer Punktladung q durch
eine beliebige geschlossenen Fläche, welche die Ladung umschließt. Diese
Fläche kann beliebig genau aufgebaut werden durch Kugeloberflächensegment,
die verbunden sind durch planare, radial nach außen verlaufende Seitenflächen.
~
jedem Punkt der Kugeloberfläche parallel ist zu der des Flächenvektors dA.
Da das elektrische Feld in jedem Punkt der Kugeloberfläche A den konstanten
Betrag E = q/4πε0 r2 hat, und die Oberfläche A der Kugel gegeben ist durch
A = 4πr2 , ergibt sich der Fluss des elektrischen Feldes durch eine Kugeloberfläche mit der Ladung q im Zentrum
I
q
q
~ dA
~=
E
4πr2 =
.
(1.46)
2
4πε0 r
ε0
A
Dieser Sachverhalt lässt sich nun direkt verallgemeinern auf beliebige geschlossene Flächen, welche die Ladung q umschliessen. Eine beliebige Fläche, welche
die Ladung q umschließt, kann nämlich, wie in Abb. 1.10 dargestellt wird, beliebig genau aufgebaut werden durch eine immer feiner werdende Überlagerung
von geeigeten Ausschnitten aus Kugeloberflächen, die verschiedene Radien haben und in deren Zentrum sich die Ladung q befindet, sowie planaren Seitenflächen, die diese verbinden. Der Fluß durch die planaren, radial nach außen
verlaufenden Seitenflächen ist aber Null, da das elektrische Feld tangential
in diesen Flächen liegt. Der Fluss durch die weiter außen liegenden Kugeloberflächensegmente kann direkt in Beziehung gesetzt werden mit dem Fluss
durch Flächensegmente auf einer weiter innen liegenden Kugel. Der Fluss beispielsweise durch das Kugeloberflächensegment A2 in Abb. 1.10 ist gleich dem
24
1 Grundlagen der Elektrostatik
Fluss durch das entsprechende Kugeloberflächensegment A1 auf der weiter innen liegenden Kugel. Die Argumentation hierbei ist ähnlich der, die wir weiter
oben an Hand der in Abb. 1.8 dargestellten Konfiguration geführt hatten. Der
Flächenvektor ist jetzt aber bei beiden Flächen A2 und A1 nach außen gerich~ Der Fluss durch die Fläche A2
tet, also in Richtung des elektrischen Feldes E.
ist somit positiv und berechnet sich zu
Z
A2
~ dA
~ = E2 A2 =
E
q
A2 .
4πε0 r22
(1.47)
Der Fluss durch die Fläche A1 mit dem Radius r1 ist ebenfalls positiv ist und
berechnet sich zu
Z
q
~ dA
~ = E1 A1 =
E
A1 .
(1.48)
4πε0 r12
A1
Da die beiden sphärischen Flächenelemente A1 und A2 durch die selben radial nach außen verlaufenden Strahlen begrenzt sind, gilt A2 /A1 = r22 /r12 oder
A2 = (r22 /r12 ) A1 . Für den Fluss durch die Fläche A2 erhält man damit
Z
A2
~ dA
~=
E
Z
q
q
r22
~ dA
~ .
E
A
=
A
=
1
1
4πε0 r22 r12
4πε0 r12
(1.49)
A1
Der Fluss durch die Fläche A2 ist also genau gleich groß dem Fluß durch die innen liegende Fläche A1 . Summiert man nun den Fluß durch alle außen liegende
Kugeloberflächensegmente auf, so ergibt sich, dass der Fluss des elektrischen
Feldes durch die beliebig geformte Fläche A gleich dem Fluss durch die Oberfläche einer weiter innen liegenden Kugel ist. Dieser ist aber gemäß Gl. (1.46)
gleich q/ε0 . Wir haben damit gezeigt, dass der Fluss des elektrischen Feldes
einer Punktladung durch eine beliebige geschlossene Fläche, welche die Ladung
umschließt, gleich q/ε0 ist.
Bislang haben wir den elektrischen Fluss lediglich einer Ladung q berachtet.
Wir wollen nun sehen, was sich ergibt, wenn wir für eine beliebige Ladungsverteilung den Fluss des von diesen Ladungen erzeugten elektrischen Feldes durch
eine beliebeige Fläche berechnen wollen. Im allgemeinen wird die Fläche einen
Teil der Ladungen einschließen, die restlichen aber nicht. Wir betrachten dazu
die in Abb. 1.11 dargestellte Situation. Der Einfachheit halber gehen wir davon
aus, das elektrische Feld werde lediglich von drei Ladungen erzeugt. Die Fläche
A umschließe nur die Ladungen q1 und q3 nicht aber q2 . Nach dem Superpositionsprinzip ergibt sich das Feld der drei Ladungen in jedem Raumpunkt
~ =E
~1 + E
~2 + E
~ 3 , wobei E
~ i , i = 1, 2, 3, das elektrische Feld der jeweilizu E
gen Punktladung qi bedeutet. Damit ergibt sich für den Fluß des elektrischen
1.5 Das GAUSSsche Gesetz für das elektrische Feld
25
Abbildung 1.11: Der Fluss des elektrischen Feldes von drei Punktladung
q1 , q2 , q3 durch eine beliebige geschlossenen Fläche, welche die Ladung q1 und
q3 umschließt, nicht aber q2 .
Feldes der drei Ladungen
I
~ dA
~=
E
A
I ~1 + E
~2 + E
~ 3 dA
~ .
E
A
Da das Integral der Summe von Funktionen gleich der Summe der Integrale
ist, folgt
I
I
I
I
~ dA
~= E
~ 1 dA
~+ E
~ 2 dA
~+ E
~ 3 dA
~ .
E
(1.50)
A
A
A
A
Die Integrale auf der rechten Seite von Gl. (1.50) stellen den Fluss des elektrischen Feldes der einzelnen Punktladung qi durch die Fläche A dar. Nach
dem oben Bewiesenen ist der Fluss des elektrischen Feldes einer Punktladung
durch eine beliebige geschlossene Fläche gleich q/ε0 , wenn die Ladung von
dieser Fläche umschlossen wird, sonst ist er Null. Das liefert
I
A
~ dA
~ = q1 + 0 + q3 = Q ,
E
ε0
ε0
ε0
wobei Q = q1 + q3 die gesamte von der Fläche A umschlossene Ladung ist. Da
die obige Argumentation direkt auf beliebige Ladungsverteilungen übertragen
werden kann, ist das GAUSSsche Gesetz damit bewiesen.
Es sei noch einmal ausdrücklich darauf hingewiesen, dass in dem
~ in dem Flussintegral das
GAUSSschen Gesetz (1.44) das elektrische Feld E
Feld ist, das von allen Ladungen herrührt, sowohl die innerhalb, als auch die
außerhalb der geschlossenen Fläche liegen, während Q auf der rechten Seite
der Gl. (1.44) nur die Ladungen umfasst, die sich innerhalb der geschlossenen
Fläche befinden.
26
1 Grundlagen der Elektrostatik
Wir wollen hier schnell noch eine Folgerung aus dem GAUSSschen Gesetzt
ziehen. Wir brauchen dazu den Begriff der Feldlinie. Eine Feldlinie ist nichts
anderes, als eine Kurve die überall tangential zu dem elektrischen Feld verläuft,
siehe Abb. 1.12. Der Feldlinienverlauf gibt somit zunächst nur die Richtung des
Feldes wieder. Wir werden aber sehen, dass der Feldlinien Verlauf auch eine
Aussage über den Betrag des Feldes macht. Wir betrachten dazu eine kleine
Querschnittsfläche A1 , die senkrecht zum Feldlinienverlauf orientiert sei. Folgt
man dem Verlauf der Feldlinien, so ändert sich diese Fläche, verkleinert sich
z.B. auf die in Abb. 1.12 dargestellten Fläche A2 . Wir betrachen nun den Fluss
des elektrischen Feldes durch die Oberfläche des röhrenförmigen Gebildes bestehend aus den Frontflächen A1 und A2 und einer Mantelfläche die parallel
zum Verlauf der Feldlinien liegt. Da die Flächen A1 und A2 als sehr klein vorausgesetzt wurden, kann das elektrische Feld auf ihnen als konstant angenommen werden. Es habe auf der Fläche A1 den Betrag E1 und auf der Fläche A2
den Betrag E2 und steht jeweils senkrecht auf diesen Flächen. Der Fluss des
elektrischen Feldes durch die Oberfläche dieses röhrenförmigen Körpers (die
Flächennormalen sind wie üblich überall nach außen orientiert) ergibt sich zu
I
A
~ dA
~ = −E1 A1 + E2 A2 .
E
Da die geschlossene Oberfläche keine Ladungen umschließt, muss nach dem
GAUSSschen Gesetz der Fluss des elektrischen Feldes durch diese Oberfläche
verschwinden, also
E2 A2 = E1 A1 .
Das bedeutet aber, dass der Betrag des elektrischen Feldes groß ist, da wo die
Feldlinien eng beieinanderliegen, und umgekehrt. Der Feldlinienverlauf macht
also auch eine Aussage über den Betrag des elektrischen Feldes.
Abbildung 1.12: Die Feldlinien eines elektrischen Feldes.
Kapitel 2
Anwendungen der Gesetze der
Elektrostatik
Das elektrostatische Feld wird vollständig durch die folgenden beiden Gesetze
beschrieben. Zum einen gilt das GAUSSsche Gesetz:
I
A
~ dA
~= Q ,
E
ε0
(2.1)
~ durch eine geschloswelches aussagt, dass der Fluss des elektrischen Feldes E
sene Oberfläche A gleich der gesamten Ladung Q ist, die sich innerhalb dieser
Fläche befindet, dividiert durch ε0 . Zum anderen gilt
I
~ d~r = 0 ,
E
(2.2)
C
~ gleich Null ist.
welches aussagt, dass die Zirkulation des elektrischen Feldes E
In diesem Kapitel wollen wir diese Gesetze benutzen, um das elekrische Feld
von verschieden Ladungskonfigurationen zu berechnen.
2.1
Das elektrische Feld einer ebenen Ladungsverteilung
Als erstes wollen wir das elektrische Feld einer unendlich ausgedehnten, ebenen,
homogenen Ladungsverteilung berechnen. Aus Symmetriegründen folgt sofort,
~ nur senkrecht auf der geladenen Ebene stehen kann, sowie rechts und
dass E
links von der Ebene den gleichen Betrag haben muss, siehe Abb. 2.1. Für die
Anwendung des GAUSSschen Satzes wird eine geeignete geschlossene Fläche
27
28
2 Anwendungen der Gesetze der Elektrostatik
Abbildung 2.1: Zur Berechnung des elektrischen Feldes einer unendlich ausgedehnten, ebenen Ladungsverteilung.
mit den planaren Seitenflächen A1 und A2 verwendet, die einen Teil Q der
Flächenladung umschließt, siehe Abb. 2.1. Wir berechnen nun den Fluss durch
~ steht senkrecht auf den beiden großen Seitendiese geschlossenen Fläche. E
flächen A1 und A2 , liegt dagegen aber parallel zu den übrigen vier schmalen
Teilflächen. Daher tragen nur die Flächen A1 und A2 zum Fluss bei, und das
GAUSSsche Gesetz liefert:
E1 A1 + E2 A2 =
Q
.
ε0
(2.3)
Mit A1 = A2 = A und |E1 | = |E2 | = E folgt:
E=
1 Q
σ
=
,
2 ε0 A
2 ε0
(2.4)
wobei σ = Q/A die Flächenladungsdichte der geladenen Schicht ist. Bemerkenswert ist, dass das elektrische Feld in jedem Abstand von einer unendlich
ausgedehneten, geladenen Schicht den gleichen Wert hat.
2.2
Das elektrische Feld einer linearen Ladungsverteilung
In diesem Abschnitt berechnen wir das elektrische Feld einer unendlich langen,
lininenhaften Ladungsverteilung, also z.B. das elektrische Feld eines unendlich langen, geraden Drahtes, der homogen geladen sein soll. Aus Symmetriegründen kann das elektrische Feld nur senkrecht zur Drahtachse stehen und hat
2.2 Das elektrische Feld einer linearen Ladungsverteilung
29
bei allen Punkten mit demselben Abstand von dem Draht den gleichen Betrag.
Außerdem zeigt es bei einem positiv geladen Draht überall nach außen. Wir
wollen das elektrische Feld mit Hilfe des GAUSSschen Gesetzes berechen. Wir
betrachten dazu den elektrischen Fluss durch einen Zylinder mit dem Radius
r und der Länge l, dessen Symmetrieachse mit dem geladenen Draht zusam~ steht senkrecht auf der Mantelfläche des Zylinders,
menfällt, siehe Abb. 2.2. E
Abbildung 2.2: Zur Berechnung des elektrischen Feldes einer unendlich ausgedehnten, linearen Ladungsverteilung.
liegt aber parallel zu den beiden Kreisflächen A1 und A2 des Zylinders. Daher
trägt nur die Mantelfläche zum Fluss bei, nicht aber die Flächen A1 und A2 .
Der GAUSSsche Satz liefert dann
E 2πr l =
Q
,
ε0
(2.5)
wobei Q der Teil der Ladung auf dem Draht ist, der von der Zylinderfläche
umschlossen wird, und E ist der Betrag des elektischen Feldes auf der Zylindermantelfläche, also im Abstand r vom Draht. Aus Gl. (2.5) folgt
E=
λ
1 Q
=
.
2πε0 r l
2πε0 r
(2.6)
Hierbei bezeichnet λ = Q/l die Linienladungsdichte, d.h. die Ladung pro
Längeneinheit. Das elektrische Feld eines unendlich langen, geraden Drahtes
fällt also mit 1/r nach außen ab.
30
2.3
2 Anwendungen der Gesetze der Elektrostatik
Das elektrische Feld einer homogen geladenen Kugel
In diesem Abschnitt berechnen wir das elektrische Feld einer homogen geladenen Kugel, sowohl im Außenraum der Kugel als auch im Innern der Kugel.
Die gesamte Ladung der Kugel sei Q und ihr Radius sei R0 . Auch hier wollen
wir für die Berechnung des elektrischen Feldes das GAUSSsche Gesetz anwenden. Dazu betrachten wir eine Kugelfläche A mit dem Radius r, welche, wie
in Abb. 2.3 dargestellt, die homogen geladene Kugel konzentrisch umschließt
(r > R0 ). Aus Symmetriegründen kann das elektrische Feld nur radial nach außen gerichtet sein und steht daher senkrecht auf der GAUSSschen Integrationsfläche. Weiter kann der Betrag des elektrischen Feldes aus Symmetriegründen
nur vom Abstand r vom Kugelmittelpunkt abhängen. Das GAUSSsche Gesetz
Abbildung 2.3: Zur Berechnung des elektrischen Feldes einer homogen geladenen Kugel.
angewendet auf die Kugelfläche A mit A = 4πr2 liefert dann
E 4πr2 =
oder
E=
1 Q
4πε0 r2
Q
ε0
für r > R0 .
(2.7)
(2.8)
Das elektrische Feld einer homogen geladenen Kugel fällt also im Außenraum
mit 1/r2 nach außen ab. Durch Vergleich mit Gl. (1.11) zeigt sich weiter, dass
das Feld im Außenraum identisch ist mit dem Feld einer Punktladung, bei
welcher die gesamte Kugelladung Q im Kugelmittelpunkt konzentriert ist.
31
2.4 Elektrische Felder von Leitern
Nun wollen wir noch das elektrische Feld im Innnern einer homogen geladenen Kugel berechnen. Das elektrische Feld ist aus Symmatriegründen auch im
Innern radial nach außen gerichtet. Wir berechen jetzt den Fluss durch eine
sphärische Fläche A, die innerhalb der Kugel liegt (r < R0 ). Sie umschließt
den Teil Q r3 /R03 der Gesamtladung Q. Das GAUSSsche Gesetz angewendet
auf die Kugelfläche A mit A = 4πr2 liefert dann
E 4πr2 =
oder
E=
1 Qr
4πε0 R03
r3
1
Q 3
ε 0 R0
für r < R0 .
(2.9)
(2.10)
Das elektrische Feld einer homogen geladenen Kugel wächst also im Innenraum
proportional zu r nach außen an. In Abb. 2.4 ist das elektrische Feld innerhalb
und außerhalb einer homogen geladenen Kugel als Funktion von r graphisch
dargestellt.
Abbildung 2.4: Das elektrische Feld innerhalb und außerhalb einer homogen
geladenen Kugel als Funktion von r.
2.4
Elektrische Felder von Leitern
Elektrische Leiter besitzen frei bewegliche Elektronen. Bringt man eine zusätzliche Ladung Q auf den Leiter, so verteilt sich diese, bis ein Gleichgewichtszustand erreicht ist. Dieser ist dadurch gekennzeichnet, dass im Innern des
~ = 0 gelten muss. Denn solange noch irgendwo im Innern des Leiters
Leiters E
~ 6= 0 gilt, würden die frei beweglichen Ladungsträger eine Kraft erfahren und
E
in Bewegung gesetzt werden, so dass noch nicht von einem stationären Zustand
32
2 Anwendungen der Gesetze der Elektrostatik
gesprochen werden kann. Wenn wir also einen Leiter im Kontext der Elektrostatik betrachten, muss das elektrische Feld in seinem Innern verschwinden.
Dies bedeutet wegen des GAUSSschen Gesetzes aber auch, dass überall im
Innern des Leiters die Ladungsdichte verschwinden muss, d.h. ̺ = 0. Man lege dazu, wie in Abb. 2.5 dargestellt, eine beliebige geschlossene GAUSSsche
~ = 0 gilt, ist
Fläche in das Innere des Leiters. Da im gesamten Leiterinneren E
der Fluss durch die Fläche Null, und damit ist nach dem GAUSSschen Gesetz
auch die gesamte von der Fläche umschlossene Ladung gleich Null. Da dies für
beliebeige geschlossene Flächen gilt, muss überall im Innern des Leiters ̺ = 0
gelten.
Abbildung 2.5: Im Innern eines Leiters gilt im elektrostatischen Gleichgewicht
~ = 0 und ̺ = 0.
E
~ = 0 überall im Innern des Leiters folgt ferner, dass sich alle Punke des
Aus E
Leiters auf dem gleichen Potential befinden. Das bedeutet aber, dass das ele~ überall senkrecht auf der Oberfläche eines Leiters stehen muss.
trische Feld E
Mit Hilfe des GAUSSschen Gesetzes können wir nun eine Beziehung herleiten
~ an der Leiteroberfläche und der dort vorhanzwischen dem elektrische Feld E
denen Flächenladungsdichte σ. Man lege dazu, wie in Abb. 2.6 dargestellt, eine
zylinderförmige, geschlossene GAUSSsche Fläche so durch die Oberfläche des
Leiters, dass die eine Hälfte innerhalb und die andere Hälfte außerhalb des Leiters liegt. Die Längenausdehnung des Zylinders sei vernachlässigbar klein, so
dass nur die beiden kreisförmigen Flächen der Größe A zum elektrische Fluss
~ = 0 gilt, und E
~ unmittelbar außerhalb des
beitragen. Da im Leiterinnern E
Leiters senkrecht auf der Leiteroberfläche steht, folgt mit dem GAUSSschen
33
2.4 Elektrische Felder von Leitern
Gesetz
EA=
Q
,
ε0
wobei Q der Teil der Ladung auf der Leiteroberfläche ist, der von dem Zylinder
umschlossen wird. Damit folgt für das elektrische Feld an der Oberfläche eines
elektrischen Leiters:
σ
E=
,
(2.11)
ε0
wobei σ = Q/A die Flächenladungsdichte an der Oberfläche des Leiters bezeichnet.
Abbildung 2.6: Zur Berechnung des elektrischen Feldes an der Oberfläche eines
Leiters.
Wir betrachten nun speziell das elektrische Feld einer geladenen Metallkugel mit dem Radius R0 und der gesamten Ladung Q. Im Innern der Kugel
~ = 0. Die Flächenladungsdichte ist
verschwindet das elektrische Feld, d.h. E
aus Symmetriegründen auf der ganzen Kugeloberfläche konstant und hat den
Wert σ = Q/4πR02 . Für das elektrische Feld an der Kugeloberfläche fogt dann
aus Gl. (2.11):
1 Q
.
(2.12)
E0 =
ε0 4πR02
Das elektrische Feld im Außenraum erhält man auf die gleiche Weise wie in
Kapitel 2.3. Es ergibt sich zu
E=
1 Q
4πε0 r2
(2.13)
34
2 Anwendungen der Gesetze der Elektrostatik
und ist somit auch hier identisch mit dem Feld einer Punktladung, bei welcher die gesamte Kugelladung Q im Kugelmittelpunkt konzentriert ist. Das
elektrische Potential lautet dann
ϕ=
1 Q
.
4πε0 r
(2.14)
Das Potential speziell an der Kugeloberfläche ergibt sich zu
ϕ0 =
1 Q
.
4πε0 R0
(2.15)
Mit den Gln. (2.12) und (2.15) kann man das elektrische Feld an der Kugeloberfläche auch durch das Potential an der Kugeloberfläche ausdrücken. Es
gilt:
ϕ0
E0 =
.
(2.16)
R0
Das elektrische Feld verhält sich also umgekeht proportional zum Radius der
Kugel. Das hat folgende Konsequenz. Wenn wir beispielsweise, wie in Abb. 2.7
dargestellt, eine große und eine kleine Kugel mit einem Draht verbinden, und
somit beide auf das gleiche Potential bringen, so ist nach Gl. (2.15) die elektrische Feldstärke an der Oberfläche der kleinen Kugel deutlich größer als an
der Oberfläche der großen Kugel. Für beliebig geformte Leiter wie in Abb. 2.8
Abbildung 2.7: Zwei mit einem Draht verbundene Metallkugeln. Sie befinden
sich auf dem gleichen Potential. Die elektrische Feldstärke an der Oberfläche
der kleinen Kugel ist deutlich größer als an der Oberfläche der großen Kugel.
bedeutet das, dass die Feldstärke im Allgemeinen umgekehrt proportional zum
Krümmungsradius an der Leiteroberfläche ist. Um bei Hochspannungsgeräten
das Auftreten hoher Feldstärken zu verhindern, ist es daher notwendig, nur abgerundete Metallteile mit großem Krümmungsradius zu verwenden und nach
Möglichkeit jede Art von Spitzen zu vermeiden. Andererseits kann man sich
die hohen Feldstärken an Spitzen zunutze machen. Ein Beispiel hierfür ist
35
2.5 Der FARADAYsche Käfig
Ladungsübertragung. Da nach Gl. (2.15) die elektrische Feldstärke an Metalloberflächen proportional zur Flächenladungsdichte σ ist, kann man mit einem
Löffel von der Spitze der Leiteroberfläche in Abb. 2.8 eine größere Ladungsmenge abstreifen als von einer weniger stark gekrümmten Stelle der Oberfäche.
Eine weiter wichtige Anwendung findet man beim Aufbau eines FeldionenMikroskops.
Abbildung 2.8: Das elektrische Feld an der Oberfläche eines beliebig geformten
Leiters. Die elektrische Feldstärke ist umgekehrt proportional zum jeweiligen
Krümmungsradius an der Leiteroberfläche.
2.5
Der FARADAYsche Käfig
Als nächstes wollen wir zeigen, dass das elektrische Feld nicht nur im Innern
von Leitern verschwindet, sondern auch in Hohlräumen von Leitern. Vorausgesetzt ist dabei, dass der Hohlraum keine Ladungen enthält. Da das elektrische
Feld, wie wir im vorigen Abschnitt gesehen haben, im Inneren eines Leiters
Null ist, verschwindet auch der Fluss des Feldes durch eine beliebige Fläche A,
die vollständig im Innern des Leiters liegt und den Hohlraum ganz umschließt,
siehe Abb. 2.9. Dies bedeutet nach dem GAUSSschen Gesetz, dass auf der
Oberfläche des innneren Hohlraumes die Gesamtladung Null sein muss. Das
schließt aber nicht aus, dass beispielsweise positive Ladungen auf der einen
und negative Ladungen auf der anderen Seite dieser Oberfläche sitzen, was zu
einem elektrischen Feld im Hohlraum führen würde. Um zu beweisen, dass das
elektrische Feld tatsächlich im Hohlraum verschwindet, machen wir erstmalig
von Gl. (2.2) Gebrauch, die ausdrückt, dass das elektrostatische Feld wirbelfrei
ist:
I
~ d~r = 0 .
E
(2.17)
C
36
2 Anwendungen der Gesetze der Elektrostatik
Abbildung 2.9: Geschlossene GAUSSsche Fläche A im Innern eines Leiters, die
den Hohlraum umschließt.
Abbildung 2.10: Für die Auswertung des Linienintergrals in Gl. (2.17) wählen
wir eine geschlossene Kurve C, die teilweise im Innern des Leiters und teilweise
durch den Hohlraum verläuf.
Als Integrationsweg für dieses Linienintergral wählen wir eine beliebige geschlossene Kurve C, die teilweise durch den Leiter und teilweise durch den
~ = 0 gilt, verschwindet
Hohlraum verläuf, siehe Abb. 2.10. Da im Leiter E
der Beitrag zum Integral in Gl. (2.17), entlang des Teils der Kurve, der im
Leiter verläuft. Da das Gesamtintegral über die geschlossene Kurve verschwindet, muß auch der Beitrag entlang des Kurvenstücks im Hohlraum Null sein.
Da dies für beliebige Integrationswege gilt, die durch den Hohlraum verlaufen,
~ = 0 gelten. Natürlich ist hierbei vorausgesetzt,
muss im gesamten Hohlraum E
2.5 Der FARADAYsche Käfig
37
dass sich keine Ladungen im Inneren des Hohlraums befinden.
Diese Feldfreiheit von metallischen Hohlräumen wird in der Elektrotechnik
zur Abschirmung von elektrischen Feldern ausgenutzt. So erreicht man im sogenannten FARADAYschen Käfig eine vollständige Abschirmung elektrischer
Felder. Die Feldfreiheit metallischer Hohlräume kann auch zur Erzeugung hoher Spannungen genutzt werden. Bringt man (siehe Abb. 2.11a) von einer
Ladungsquelle mit einem Löffel“
Ladungen in das Innere einer metalli”
schen Hohlkugel, so wandern die Ladungen sofort nach außen und der innere
Hohlraum bleibt feldfrei, unabhängig davon wieviel Ladungen die Hohlkugel
bereits trägt. Durch wiederholtes Transportieren von Ladungen von einer positiven Ladungsquelle, die sich auf dem Potential U0 befindet, wobei man immer
wieder die gesamte Ladung des Löffels auf die Hohlkugel überträgt, kann diese
schließlich ein viel höheres Potential erreichen als die Ladungsquelle. Entscheidend ist dabei das Abstreifen der Ladung des Löffels im feldfreien Inneren der
Hohlkugel! Bei dem VAN DE GRAAFF-Generator (siehe Abb. 2.11b) wird
dieses Verfahren automatisiert“. Die Ladung wird durch ein rotierendes, iso”
Abbildung 2.11: Durch Wiederholtes Aufbringen von kleinen Ladungsmengen
in das Innere einer Metall-Hohlkugel kann die Hohlkugel auf sehr hohe Spannung aufgeladen werden (Bild a). Prinzip des VAN DE GRAAFF-Generator
(Bild b).
38
2 Anwendungen der Gesetze der Elektrostatik
lierendes Band in das Innere der Hohlkugel übertragen. Unten werden dabei
z.B. positive Ladungen von dem positiven Pol einer Ladungsquelle auf das
Band gesprüht, dann nach oben transportiert und schließlich oben im Innern
der Hohlkugel wieder abgestreift. Auf diese Weise kann man erreichen, dass
sich die Kugel bis auf etwa 10 Millionen Volt auflädt.
2.6
Influenz
Wir hatten in Abschnitt 2.4 gesehen, dass das elektrische Feld im Innern eines
Leiters verschwindet. Hier wollen wir noch etwas genauer verstehen, wie es
zu der Auslöschung des elektrischen Felds in einem Leiter kommt. Bringen wir
einen Leiter, z.B. ein beliebiges Stück Metall, in das elektrische Feld eines Plattenkondensators, so werden unter dem Einfluss des Feldes Ladungen in dem
Leiter getrennt. Es bilden sich sogenannte Influenzladungen, siehe Abb. 2.12.
Sie verursachen im Innern des Leiters ein Feld, das dem ursprünglichen entgegengerichtet ist und dieses exakt zu Null kompensiert. Genau aus diesem
Grund verschwindet letztlich das elektrische Feld in einem Leiter.
Abbildung 2.12: Ein beliebiger Leiter im Feld eines Plattenkondensators Die
Influenzladungen verteilen sich so auf der Leiteroberfäche, dass das elektrische
Feld im Innern des Leiters verschwindet.
Das Auftreten der Influenzladungen kann in dem folgenden Versuch noch
genauer demonstriert werden, siehe Abb. 2.13. Wir pressen zwei flache Aluminiumscheiben, die jeweils an einem isolierenden Stil befestigt sind (La~ (siehe
dungslöffel), zusammen und bringen sie in eine elektrisches Feld E
Abb. 2.13a). Die Influenzladungen sammeln sich an den nach außen gerichteten Oberflächen der Aluminiumscheiben. Das elektrische Feld im Innern der
2.7 Kapazität
39
Scheiben verschwindet. Die Scheiben mit den Influenzladungen werden nun in
dem äußeren Feld getrennt (siehe Abb. 2.13b). Das Feld zwischen den Scheiben bleibt weiterhin Null. Nun werden die getrennten Scheiben aus dem Feld
~ herausgenommen (siehe Abb. 2.13c). Zwischen den getrennten Scheiben exiE
~ ′ , das genau
stiert dann auf Grund der Influenzladungen ein elektrisches Feld E
~ aber entgegengesetzt gerichtet ist, d.h. E
~ ′ = −E.
~ Die Influenzso groß wie E,
ladungen können nun mit einem Elektrometer gemessen werden, und so kann
auf diese Weise die eletrische Feldstärke gemessen werden.
Abbildung 2.13: Demonstrationsversuch zum Nachweis der Influenzladungen.
2.7
Kapazität
Als nächstes wollen wir uns mit einem isolierten Leiter beschäftigen, der die
Ladung Q trägt und dessen Potential ϕ sei, wobei der Nullpunkt des Potentials
40
2 Anwendungen der Gesetze der Elektrostatik
im Unendlichen liegen soll. Das Potential enspricht damit der Spannungsdifferenz U = ϕ gegenüber dem Unendlichen. Der Quotient aus U und Q wird
dann als Kapazität des Leiters definiert und mit C bezeichnet,
C=
Q
.
U
(2.18)
Die Kapazität gibt also die pro Spannungseinheit auf dem Leiter gespeicherte
Ladung an. Sie wird gemessen in der Einheit Farad (F), wobei nach Gl. (2.18)
gilt F = C/V.
Als Beispiel betrachten wir eine homogene, leitende Kugel mit dem Radius
R0 . Nach Gl. (2.15) ist das Potential an der Kugeloberfläche
ϕ0 =
1 Q
.
4πε0 R0
(2.19)
Dies enspricht der Spannung U gegenüber dem Unendlichen, und damit ergibt
sich für die Kapazität C = Q/U einer leitenden Kugel:
C = 4 π ε 0 R0 .
(2.20)
Für technische Anwendungen verwendet man zur Speicherung von Ladungen in der Regel zwei Leiter, die mit den entgegengesetzten Ladungen Q und
−Q geladenen sind, siehe Abb. 2.14. Eine solche Anordnung wird als Kondensator bezeichnet. In diesem Fall ist die Kapazität C der Quotient aus der
Ladung Q und der Spannungsdifferenz U zwischen den beiden Leitern. Die
Kapazität ist also auch hier gegeben durch Gl. (2.18)
C=
Q
,
U
(2.21)
Abbildung 2.14: Eine allgemeine Anordnung zur Speicherung von Ladung. Sie
wird als Kondensator bezeichnet.
41
2.7 Kapazität
wobei die Spannungsdifferenz U zwischen den beiden Leitern gemäß Gl. (1.25)
gegeben ist durch
U = ϕ(~r+ ) − ϕ(~r− ) =
Z~r−
~ d~r .
E
(2.22)
~
r+
Hierbei ist ~r+ ein beliebiger Punkt auf dem positiv geladenen Leiter und ~r− ein
beliebiger Punkt auf dem negativ geladenen Leiter. Insbesondere können die
Punkte natürlich auf der Oberfläche des jeweiligen Leiters liegen. Im folgenden
wird nun die Kapazität von verschiedenen Leiteranordnungen berechnet.
Als erstes betrachten wir den Plattenkondensator. Hier stehen sich zwei geladene Platten gegenüber, siehe Abb. 2.15. Die linke Platte habe die Ladung
Q die rechte die Ladung −Q. Der Abstand d der Platten sei klein gegenüber
den Abmessungen der Fläche A der Platten, so dass das elektrische Feld in
dem Zwischenraum als homogen angenommen werden kann. Das Feld dieser
Abbildung 2.15: Plattenkondensator. Das elektrische Feld ergibt sich durch
Superposition der Felder zweier entgegengesetzt geladener Platten gleicher Ladung.
Anordnung erhält man durch Superposition der Felder der beiden, entgegengesetzt geladenene Platten. Das von der positiv geladenen Platte erzeugte Feld
~ + , das von der negativ geladenen Platte erzeugte Feld mit E
~ − bewird mit E
zeichnet, siehe Abb. 2.15. Für den Betrag beider Felder gilt nach Gl. (2.4)
E+ = E− = σ/(2 ε0 ), wobei σ = Q/A die Flächenladungsdichte der geladenen
Platten ist. Wie man sieht, kompensieren sich die Felder im Außenraum, im
Innenraum dagegen verdoppelt sich das Feld. Das Feld zwischen den Platten
hat damit den Wert
σ
1 Q
E=
=
.
(2.23)
ε0
ε0 A
42
2 Anwendungen der Gesetze der Elektrostatik
Dieses Feld ist im gesamten Raum zwischen den Platten der Richtung und
dem Betrag nach gleich und ist unabhängig vom Abstand d der Platten. Das
Potential zwischen den Platten (die positiv geladene Platte befinde sich bei
x = 0, die negativ geladene bei x = d) ergibt sich gemäß Gl. (1.17) zu
ϕ(x) = −
Z
x
d
E dx =
Z
d
x
E dx = E (d − x) ,
(2.24)
wobei wir die negativ geladene Platte zum Nullpunkt des Potentials gewählt
haben. Für die Spannung zwichen den Platten erhalten wir aus Gl. (2.24)
U = ϕ(0) − ϕ(d) = E d .
(2.25)
Mit Gln. (2.21), (2.25) und (2.23) ergibt sich die Kapazität eines Plattenkondensators zu:
A
.
(2.26)
C = ε0
d
Als nächstes wollen wir die Kapazität eines Zylinderkondensators berechnen. In der Praxis kann es sich dabei auch um ein Koaxialkabel handeln. Der
Zylinderkondensator besteht aus zwei koaxial ineinander gesteckten Zylindern.
Der innere Zylinder mit dem Radius ri habe die Ladung Q, der äußere mit
dem Radius ra die Ladung −Q. Beide haben die Länge l, siehe Abb. 2.16. Wir
nehmen an, dass die Längenausdehnung viel größer ist als die radialen Abmessungen, l ≫ ra , wodurch Randeffekte vernachlässigbar sind. Zur Berechnung
des elektrischen Feldes benutzen wir das GAUSSsche Gesetz. Die Betrachtung ist dabei ganz ähnlich der in Kap. 2.2. Wir betrachten den elektrischen
Fluss durch einen Zylinder mit dem Radius r und der Länge l, dessen Symmetrieachse mit der des Kondensators zusammenfällt. Das elektrische Feld ist
nach außen gerichtet. Es kann aus Symmetriegründen nur senkrecht zur Zylinderachse stehen und hat bei allen Punkten mit demselben Abstand von der
Zylinderachse den gleichen Betrag. Wählen wir für den Radius des Zylinders
r < ri , so tritt kein Fluß durch die GAUSSsche Fläche, da keine Ladung umschlossen wird. Das elektrische Feld innerhalb der inneren Kondensatorfläche
ist somit Null. Das gleiche gilt für das elektrische Feld im Außenraum. Auch
hier wird von der GAUSSschen Fläche keine Ladung umschlossen, da sich die
Ladungen Q und −Q aufheben. Legen wir die GAUSSsche Fläche aber, wie in
Abb. 2.16 dargestellt, in den Zwischenraum zwischen die beiden Flächen des
Kondensators, ri < r < ra , so folgt mit dem GAUSSschen Gesetz
E 2πr l =
Q
.
ε0
(2.27)
43
2.7 Kapazität
Abbildung 2.16: Zylinderkondensator. Das elektrische Feld im Innern des Kondensators läßt sich berechnen mit Hilfe des GAUSSschen Gesetzes.
Dabei trägt nur die Mantelfläche des GAUSSschen Zylinders zum Fluss bei,
nicht aber die kreisförmigen Begrenzungsflächen an den beiden Enden, da das
elektrische Feld tangential in diesen Flächen liegt. Für das elektrische Feld
folgt aus Gl. (2.27)
Q
E=
.
(2.28)
2πε0 l r
Für das Potential im Bereich zwischen den zylindrischen Platten des Kondensators folgt mit Gl. (1.17)
Q
Q
ra
,
(2.29)
dr =
ln
2πε0 l r
2πε0 l
r
r
r
ra
wobei wir den negativ geladenen äußeren Zylinder zum Nullpunkt des Potentials gewählt haben. Für die Spannung zwischen den beiden Zylindern erhalten
wir aus Gl. (2.29)
ϕ=−
Z
r
E dr =
Z
ra
E dr =
Z
ra
ra
Q
ln
U = ϕ(ri ) − ϕ(ra ) =
2πε0 l
ri
.
(2.30)
Mit Gln. (2.21) und (2.25) ergibt sich die Kapazität eines Zylinderkondensators
(oder Koaxialkabels) der Länge l zu:
C=
Q
=
U
Q
Q
2πε0 l
ln
ra
ri
=
2πε0 l
ln
ra
ri
.
(2.31)
44
2 Anwendungen der Gesetze der Elektrostatik
Als letztes betrachten wir einen Kugelkondensator. Der Kugelkondensator
besteht aus zwei konzentrisch ineinander gesteckten Kugeln. Die innere Kugel mit dem Radius ri trage die Ladung Q, die äußere mit dem Radius ra die
Ladung −Q. Ein solcher Kugelkondensator ist in Abb. 2.17 dargestellt. Zur Be-
Abbildung 2.17: Kugelkondensator (Schnittbild). Das elektrische Feld im Innern des Kondensators läßt sich berechnen mit Hilfe des GAUSSschen Gesetzes.
rechnung des elektrischen Feldes benutzen wir wieder das GAUSSsche Gesetz.
Die Betrachtung ist dabei ganz ähnlich der in Kap. 2.3. Wir betrachten den
elektrischen Fluss durch eine Kugel mit dem Radius r deren Mittelpunkt mit
dem des Kugelkondensators zusammenfällt. Aus Symmetriegründen kann das
elektrische Feld nur radial nach außen zeigen und hat bei allen Punkten mit
demselben Abstand vom Mittelpunkt der Kugel den gleichen Betrag. Wählen
wir für den Radius der Kugel r < ri , so tritt kein Fluß durch die GAUSSsche
Fläche, da keine Ladung umschlossen wird. Das elektrische Feld innerhalb der
inneren Kondensatorfläche ist somit Null. Das gleiche gilt für das elektrische
Feld im Außenraum. Auch hier wird von der GAUSSschen Fläche keine Ladung umschlossen, da sich die Ladungen Q und −Q aufheben. Legen wir die
GAUSSsche Fläche aber, wie in Abb. 2.16 dargestellt, in den Zwischenraum
zwischen die beiden Flächen des Kondensators, ri < r < ra , so folgt mit dem
GAUSSschen Gesetz
E 4πr2 =
Q
.
ε0
(2.32)
45
2.7 Kapazität
Für das elektrische Feld folgt aus Gl. (2.32)
E=
1 Q
.
4πε0 r2
(2.33)
Für das Potential im Bereich zwischen den kugelförmigen Platten des Kondensators folgt mit Gl. (1.17)
ϕ=−
Z
r
ra
E dr =
Z
ra
r
E dr =
Z
ra
r
1 Q
Q
dr =
2
4πε0 r
4πε0
1
1
−
r ra
,
(2.34)
wobei wir die negativ geladene äußere Kugel zum Nullpunkt des Potentials
gewählt haben. Für die Spannung zwischen den beiden Kugeln erhalten wir
aus Gl. (2.34)
U = ϕ(ri ) − ϕ(ra ) =
Q
4πε0
1
1
−
ri ra
=
Q
4πε0
ra − ri
ra ri
.
(2.35)
Mit Gln. (2.21) und (2.35) ergibt sich die Kapazität eines Kugelkondensators
zu:
Q
ra ri
C=
.
(2.36)
= 4πε0
U
ra − ri
Durch Parallel- und Serienschaltung von Kondensatoren lassen sich neue
Kapazitäten herstellen. Bei der Parallelschaltung von zwei Kondensatoren, siehe Abb. 2.18a, liegt an beiden die gleiche Spannung U . Es gilt:
Q = Q1 + Q2 = C1 U + C2 U = (C1 + C2 ) U .
Vergleicht man dies mit der Definitionsgleichung für die Kapazität Q = C U ,
so sehen wir: Die Parallellschaltung zweier Kapazitäten C1 und C2 besitzt eine
Gesamtkapazität C mit
C = C1 + C2 .
(2.37)
Bei der Serienschaltung zweier Kondensatoren, siehe Abb. 2.18b, tragen beide Kondensatoren die gleiche Ladung Q. Denn wird die Anordnung mit einer
Spannungsquelle verbunden, so ist die Potentialdifferenz über die gesamte Anordnung hinweg U . Auf der linken Platte von C1 sammelt sich die Ladung Q.
Durch Influenz wird auf der rechten Platte von C1 die Ladung −Q induziert.
Diese rührt von Ladungsträgern her, die von der linken Platte von C2 abgeflossen sind, wodurch auf der linken Platte von C2 die Ladung Q verbleibt. Auf der
rechten Platte von C2 haben wir schließlich wieder wegen des Influenzeffektes
die entsprechende Ladung −Q. Da die Geamtspannung U gleich der Summe
der Spannungen U1 und U2 an den einzelnen Kondensatoren ist, folgt
Q
Q
1
1
U = U1 + U2 =
Q .
+
=
+
C1 C2
C1 C2
46
2 Anwendungen der Gesetze der Elektrostatik
Vergleicht man dies mit der Definitionsgleichung für die Kapazität U = Q/C,
so sehen wir: Die Serienschaltung zweier Kapazitäten C1 und C2 besitzt eine
Gesamtkapazität C mit
1
1
1
=
+
.
(2.38)
C
C1 C2
Abbildung 2.18: Parallelschaltung (a) und Serienschaltung (b) von Kondensatoren.
2.8
Die Energie des elektrischen Feldes
Beim Aufladen eines Kondensators muss man Arbeit verrichten, die dann als
~
elektrische Energie im E-Feld
des Kondensators gespeichert ist. Wir sehen uns
einen solche Aufladevorgang im Detail an, siehe Abb. 2.19. Die momentane
Ladung des Kondensators betrage q, die Spannung u = q/C. Um eine weitere
Ladung dq von der negativen zur positiven Platte zu bewegen ist die Arbeit
dW = u dq
nötig. Die Arbeit für die gesamte Aufladung bis zur Ladung Q beträgt somit:
W =
ZQ
0
u dq =
ZQ
0
q
Q2
1
dq =
= C U2 .
C
2C
2
(2.39)
Dies ist dann die in dem elektrischen Feld des Kondensators gespeicherte Energie. Wir betrachten nun speziell einen Plattenkondensator. Seine Kapazität ist
2.8 Die Energie des elektrischen Feldes
47
Abbildung 2.19: Aufladen eines Kondensators.
gemäß Gl. (2.26) gegeben durch C = ε0 A/d. Für die Spannung zwischen den
Kondensatorplatten gilt U = E d. Für die Energie des elektrischen Feldes eines
Plattenkondensator folgt damit aus Gl. (2.39)
W =
1 A
1
1
ε0 (E d)2 = ε0 A d E 2 = ε0 E 2 V ,
2
d
2
2
wobei V = A d das Volumen in dem Plattenkondensator ist. Damit folgt für die
Energiedichte we = W/V des elektrischen Feldes in einem Plattenkondensator
we =
1
ε0 E 2 .
2
(2.40)
Wir haben Gl. (2.40) hergeleitet für das elektrische Feld eines Plattenkondensators. Es lässt sich allgemein zeigen, dass die Energiedichte eines beliebigen
elektrischen Feldes gegeben ist durch den Ausdruck in Gl. (2.40).
Zum Schluss wollen wir noch die Kraft zwischen den Platten in einem Plattenkondensator berechen. Die Platten tragen die Ladungen Q bzw. −Q. Für
das elektrische Feld zwischen den Platten gilt nach Gl. (2.23) E = Q/(ε0 A)
und es ist somit unabhängig vom Plattenabstand d (Vorausgesetzt ist wieder, dass der Abstand d der Platten klein ist gegenüber den Abmessungen der
Fläche A der Platten). Da die Platten entgegengesetzt geladen sind, ziehen
sie sich gegenseitig an mit einer Kraft vom Betrag F , welche nun berechnet
werden soll. Wir stellen dazu folgende Überlegung an. Wenn wir die Platten,
wie in Abb. 2.20 dargestellt, gegen die Wirkung dieser Kraft F um eine kleine
Strecke ∆d auseinander ziehen, so erfordert das die Arbeit
∆W = F ∆d .
(2.41)
48
2 Anwendungen der Gesetze der Elektrostatik
Abbildung 2.20: Zur Berechnung der Kraft zwischen den Platten eines Plattenkondensators.
Da das Feld unabhängig vom Plattenabstand ist, bleibt gemäß Gl. (2.40) auch
die Energiedichte konstant. Durch die Volumenzunahme ∆V = A ∆d erhöht
sich aber gemäß Gl. (2.40) die Energie des elektrischen Feldes um den Betrag
∆W =
1
ε0 E 2 A ∆d .
2
(2.42)
Dieser Energiezuwachs des Feldes muss gleich der verrichteten Arbeit sein. Aus
den Gln. (2.41) und (2.42) folgt damit:
F =
1
ε0 E 2 A ,
2
bzw. wegen E = Q/(ε0 A)
1
QE .
(2.43)
2
Dies mag überraschen, da nach Gl. (1.9) die Kraft auf eine Ladung q in einem
elektrischen Feld E gegeben ist durch F = q E. Wir müssen aber bedenken,
dass gemäß Gl. (2.4) das elektrische Feld einer Platte, z.B. der positiv geladenen gegeben ist durch
F =
E+ =
σ
E
1 Q
=
.
=
2 ε0
2 ε0 A
2
Damit wirkt auf die negative Platte mit der Ladung −Q eine Kraft vom Betrag
F = Q E+ =
in Übereinstimmung mit Gl. (2.43)
1
QE .
2
(2.44)
2.9. DAS ELEKTRISCHE FELD IN MATERIE
2.9
49
Das elektrische Feld in Materie
Während das Innere von Leitern in der Elektrostatik immer feldfrei ist, greifen elektrische Felder durch Isolatoren hindurch. Daher heißen Isolatoren auch
Dielektrika (nach dem griechischen Wort dia = durch). Der Einfluß eines Dielektrikums auf das elektrische Feld ist dabei folgender. Bringt man zwischen
die Platten eines Kondensators, auf dessen Platten sich die Ladung Q bzw.
−Q befindet, ein Dielektrikum, so verringert sich das elektrische Feld von E0
auf E. Der Faktor, um den das elektrische Feld E0 (ohne Dielektrikum) größer
ist als das elektrische Feld E (mit Dielektrikum) wird als Dielektrizitätszahl ε
bezeichnet,
E0
ε :=
.
(2.45)
E
Wegen U = E d, wobei U die Spannung zwischen den Kondensatorplatten und
d der Plattenabstand ist, sinkt auch die Spannung zwischen den Kondensatorplatten beim Einbringen des Dielektrikums um denselben Faktor wie das
elektrische Feld,
E0
U0
=
=ε .
(2.46)
U
E
Hierbei ist U0 die Spannung ohne Dielektrikum und U die Spannung mit Dielektrikum. Die Kapazität des Kondensators hingegen nimmt um den Faktor
ε zu. Denn wegen C = Q/U folgt
C
Q/U
U0
=ε .
=
=
C0
Q/U0
U
(2.47)
Hierbei ist C0 die Kapazität ohne Dielektrikum und C die Kapazität mit Dielektrikum. Dies ist dann auch eine der wichtigsten Eigenschaften von Dielektrika. Mit ihnen kann die Kapazität von Kondensatoren erheblich vergrößert
werden. Die Kapazität eines Plattenkondensators, zwischen dessen Platten sich
eine Dielektrikum mit der Dielektrizitätszahl ε befindet, ergibt sich beispielsweise wegen Gl. (2.26) zu:
A
.
C = ε ε0
d
Der Grund für die Abnahme des elektrischen Feldes im Dielektrikum liegt in
der Polarisation des Dielektrikums. Wir betrachten dazu einen Isolator im Feld
eines Plattenkondensators, siehe Abb. 2.21. Da das elektrische Feld an allen
Atomen bzw. Molekülen des Dielektrikums in gleicher Weise angreift, werden
deren negative und positive Ladungen um ein kleines Stück gegeneinander verschoben, so dass ein induziertes Dipolmoment entsteht. Diese Polarisation des
50
2 Anwendungen der Gesetze der Elektrostatik
Abbildung 2.21: Ein Dielektrikum innerhalb eines Plattenkondensators.
Dielektrikums ändert nichts an der elektrischen Neutralität im Inneren des Isolators. Sie erzeugt aber eine negative Überschussladung (−Qp ) auf der linken
Oberfläche und eine positive Überschussladung (Qp ) auf der rechten Oberfläche
des Isolators, siehe Abb. 2.21. Diese Polarisationsladungen schwächen nun das
elektrische Feld der freien Ladungen Q bzw −Q auf den Kondensatorplatten
ab, weil sie das entgegengesetzte Vorzeichen haben. In der nachfolgenden Tabelle sind Werte der Dielektrizitätszahl ε für einige Substanzen aufgelistet. Es
sind auch einige Substanten mit polaren Molekülen dabei, wie z.B. H2 O oder
SrTiO3 . Bei diesen Substanzen besitzen die Moleküle, auch ohne dass sie in ein
äußeres Feld gebracht werden, ein permanentes elektrisches Dipolmoment und
die Dielektrizitätszahl dieser Substanzen nimmt besonders große Werte an.
Substanz
Luft
HCl
H2 O
H2 O
Benzol
Porzellan
Paraffin
SrTiO3
Zustand des Mediums
gasförmig, 00 C, 1 bar
gasförmig, 00 C, 1 bar
gasförmig, 1100 C, 1 bar
flüssig, 200 C
flüssig, 200 C
fest, 200 C
Wachs, 200 C
Kristall, 10 K
ε
1,00059
1,0046
1,0126
80,0
2,28
4,0
2,1
12000
Kapitel 3
Der elektrische Strom
3.1
Strom und die Bewegung von Ladungen
Elektrische Ströme werden durch die Bewegung von Ladungsträgern (sehr
häufig Elektronen) erzeugt. Wir betrachten dazu einen Leiter mit der Querschnittsfläche A, siehe Abb. 3.1. Die Teilchenzahldichte der beweglichen Ladungsträger sei n und jeder Ladungsträger habe die Ladung q. Wir nehmen
weiter an, alle Ladungsträger bewegen sich mit der gleichen Geschwindigkeit
~vD , der Driftgeschwindigkeit. Dann fließen in dem Zeitintervall dt alle Ladungen, die sich in dem Volumen A dx = A vD dt vor einer Querschnittsfläche A
Abbildung 3.1: Die Bewegung von Ladungsträgern in einem Leiter.
51
52
3 Der elektrische Strom
befinden, durch diese Querschnittsfläche hindurch. Das ergibt für die gesamte
durch die Querschnittsfläche A transportierte Ladung
dQ = n q A vD dt .
(3.1)
Der elektrische Strom I wird nun definiert als Ladung, die pro Zeit durch eine
Querschnittsfläche des Leiters tritt, in Zeichen
I :=
dQ
.
dt
(3.2)
Die Stromstärke wird gemessen in der Einheit Ampere (A). Aus Gl. (3.2) folgt
A = C/s. Aus den Gln. (3.1) und (3.2) folgt für den elektrischen Strom
I = n q A vD .
(3.3)
In Wirklichkeit bewegen sich die Ladungsträger allerdings nicht alle mit der
gleichen Geschwindigkeit, sondern der gerichteten Bewegung der Ladungsträger ist eine viel stärkere thermische Bewegung überlagert. Die Driftgeschwindigkeit ~vD ist eigentlich gegeben durch den Mittelwert h~v i, gebildet
über alle Ladungsträger. Wir gehen darauf in Kap. 3.3 noch ausführlich ein.
Ist der Strom der Ladungsträger nicht homogen, so muss er durch die Stromdichte ~j beschrieben werden. Diese ist definiert durch
~j(~r ) = lim ∆I ~n .
∆A→0 ∆A
(3.4)
Hierbei ist ∆I der Strom, der durch die Fläche ∆A tritt, welche senkrecht
zu dem Strom ∆I orientiert ist. ~n bezeichnet die Flächennormale der Fläche
A, orientiert in Richtung des Stromes ∆I. Die Fläche ∆A zieht sich bei der
Grenzwertbildung in Gl. (3.4) auf den Raumpunkt ~r zusammen. Die Einheit
der Stromdichte ~j ergibt sich zu A/m2 . Mit Gl. (3.3) folgt für die Stromdichte
~j = n q ~vD .
(3.5)
Den gesamten Strom durch eine beliebige Fläche A im Raum erhält man durch
Bilden des Flächenintegrals
Z
~ .
I = ~j dA
(3.6)
A
Mit Hilfe der Stromdichte lässt sich noch ein wichtiges Grundprinzip der
Elektrizitätslehre formulieren, das Gesetz der Ladungserhaltung. Es sagt aus:
Die Ladung, die pro Zeit aus einer geschlossenen Fläche A herausfließt, muss
3.2 Elektrische Leitfähigkeit und das OHMsche Gesetz
53
gleich der Abnahme der Ladung Q in dem von der Fläche A umschlossenen
Volumen V sein, in Zeichen:
I
A
Z
~ = − dQ = − d ̺ dV .
~j dA
dt
dt
(3.7)
V
Obige Gleichung wird auch als Kontinuitätsgleichung bezeichnet. Ist die Ladungsdichte ̺ konstant, was in Leitern üblicherweise der Fall ist, so vereinfacht
sich Gl. (3.7) zu
I
~=0 .
~j dA
(3.8)
A
Das bedeutet, die Summe über alle zu- und abfließenden Ströme durch eine beliebige geschlossene Fläche A muss Null sein. Wir werden darauf noch
einmal in Kap. 3.5 im Zusammenhang mit den KIRCHHOFFschen Regeln
zurückkommen.
3.2
Elektrische Leitfähigkeit und das OHMsche Gesetz
Die antreibende Kraft für einen elektrischen Strom ist ein elektrisches Feld
bzw. eine elektrische Spannung, die an einem Leiter angelegt wird. Für den
Zusammenhang zwischen Strom und Spannung zeigt sich dabei experimentell
für sehr viele Leiter das OHMsche Gesetz:
Der Strom durch einen Leiter ist proportional zu der angelegten
Spannung, in Zeichen:
U = RI .
(3.9)
Die Proportionalitätskonstante R wird als OHMscher Widerstand des Leiters bezeichnet. Die Einheit für den Widerstand ist das Ohm (Ω), wobei nach
Gl. (3.9) gilt Ω = V/A. Die Aussage des OHMschen Gesetzes besteht also darin, dass der Widerstand R unabhängig von der Spannung U ist. Er hängt allerdings von der Temperatur des Leiters ab. Außerdem hängt er von der Länge
l und dem Querschnitt A des Leiters ab. Es zeigt sich dabei experimentell der
Zusammenhang
l
R=̺
.
(3.10)
A
Dabei ist ̺ der spezifische Widerstand des Leitermaterials. ̺ wird in der Einheit Ω m gemessen.
54
3 Der elektrische Strom
Man kann das OHMsche Gesetz auch noch anders formulieren, und zwar
durch einen Zusammenhang zwischen der Stromdichte ~j und dem elektrischen
~ Mit den Beziehungen U = E l und I = j A, wobei l die Länge und A
Feld E.
der Querschnitt des Leiters ist, folgt aus Gl. (3.9)
El = RjA
bzw.
l
E .
(3.11)
AR
Führen wir an dieser Stelle die spezifische Leitfähigkeit σ des Leitermaterials
ein gemäß
1
l
=
,
σ=
AR
̺
j=
so lässt sich Gl. (3.11) schreiben in der Form
j = σE ,
oder in vektorieller Schreibweise
~ .
~j = σ E
(3.12)
Gl. (3.12) ist eine lokale Formulierung des OHMschen Gesetzes. Diese ist insofern allgemeiner als Gl. (3.9), weil sie auch für inhomogene Stromverteilungen
gültig ist. Die eigentliche Aussage des OHMschen Gesetzes in der Formulierung
(3.12) ist, dass die Stromdichte ~j an irgendeinem Ort im Leiter proportional
~ an derselben Stelle ist. Das bedeutet insbesondere,
zum elektrischen Feld E
~ ist.
dass die spezifische Leitfähigkeit σ unabhängig von E
3.3
Mikroskopisches Modell für das OHMsche
Gesetz
Im Jahr 1900 schlug P.K. DRUDE ein Modell vor, das einen tieferen Einblick
in die Natur der elektrischen Leitung in Metallen gewährte und darüber hinaus
eine Herleitung des OHMschen Gesetzes erlaubte. Ausgangspunkt dieses Modells ist eine Betrachtung der mikroskopischen Bewegung der Ladungsträger
durch den Leiter. Im thermodynamischen Gleichgewicht bewegen sich die Ladungsträger (z.B. Elektronen) mit einer hohen thermischen Geschwindigkeit
durch den Leiter. Dabei erfahren sie ständig Stöße mit den nahezu raumfesten
Ionen des Leiters. Die mittlere Zeit zwischen zwei solchen Stößen sei τ . Ohne
3.3 Mikroskopisches Modell für das OHMsche Gesetz
55
~ ist die mittlere Geschwindigkeit h~v i = 0, da
ein äußeres elektrisches Feld E
die Bewegung der Ladungsträger statistisch ist und somit keine Richtung im
~ angelegt wird,
Raum ausgezeichnet ist. Sobald jedoch ein elektrisches Feld E
~
~ wobei q
erfährt jeder Ladungsträger zwischen zwei Stößen die Kraft F = q E,
die Ladung der Ladungsträger ist. Nach dem zweiten NEWTONschen Axiom
m ~a = F~ bewirkt diese Kraft die Beschleunigung
~a =
q ~
d~v
=
E ,
dt
m
wobei m die Masse der Ladungsträger ist. Durch Integration nach der Zeit t
folgt
q ~
t ,
(3.13)
~v = ~v0 + E
m
wobei ~v0 die Geschwindigkeit des Ladungsträgers direkt nach dem letzten Stoß
ist. Um daraus die mittlere Geschwindigkeit (Driftgeschwindigkeit) ~vD = h~v i
zu erhalten, müssen wir in Gl. (3.13) für irgendeinen beliebigen Zeitpunkt über
die Geschwindigkeiten aller Ladungsträger mitteln. Das liefert
h~v i = h~v0 i +
q ~
Eτ .
m
(3.14)
Hierbei ist τ die bereits erwähnte mittlere Zeit zwischen zwei Stößen. Für die
mittlere Geschwindigkeit h~v0 i der Ladungsträger direkt nach dem letzten Stoß
gilt h~v0 i = 0. Dies kann man wie folgt einsehen. Für einen normalen Strom
liegt die Driftgeschwindigkeit vD in der Größenordnung vD ≈ 10−4 m/s, wohingegen die mittlere Geschwindigkeit hvi ungefähr hvi ≈ 106 m/s beträgt. Da
hvi somit um den Faktor 1010 größer ist als vD , ist auf der mikroskopischen
Betrachtungsebene der Anteil an der Bewegung eines Ladungsträgers, der auf
das elektrische Feld zurück geht, vernachlässigbar klein. Man kann deshalb davon ausgehen, dass die Geschwindigkeit ~v0 eines Ladungsträgers direkt nach
dem Stoß wieder zufällig gerichtet ist, also h~v0 i = 0. Aus Gl. (3.14) folgt damit
~vD = h~v i =
qτ ~
E .
m
(3.15)
Wir führen an dieser Stelle die Beweglichkeit µ der Ladungsträger ein gemäß
µ=
qτ
.
m
Damit lässt sich Gl. (3.15) schreiben in der Form
~ .
~vD = µ E
56
3 Der elektrische Strom
Für die Stromdichte ~j folgt mit Gl. (3.5) schließlich
~ .
~j = n q ~vD = n q µ E
~ folgt im Rahmen dieses
Durch Vergleich mit der Beziehung (3.12), ~j = σ E,
mikroskopischen Modells für die spezifische Leitfähigkeit σ
σ = nqµ =
n q2 τ
.
m
Das OHMsche Gesetz ist bewiesen, wenn wir noch zeigen können, das σ un~ ist. Die Faktoren n, q und m sind sicher unabhängig von E,
~
abhängig von E
aber was ist mit τ ? Wir erwarten, dass τ von der mittleren Geschwindigkeit hvi
~ nur um den Betrag vD ≈ 10−4 m/s
abhängt. Da aber hvi ≈ 106 m/s durch E
~ und damit ist das OHMsche
geändert wird, ist hvi praktisch unabhängig von E,
Gesetz hergeleitet.
Man kann Gl. (3.15) noch auf folgende Weise schreiben:
~ − m ~vD = 0 .
qE
τ
Dies lässt folgende Interpretation zu. Der die Ladungsträger antreibenden
~ wirkt eine vom Betrage gleich große Kraft
Kraft q E
m
F~R = − ~vD
τ
(3.16)
entgegen. Die Ladungsträger bewegen sich also so durch den Leiter, als wenn
sie eine geschwindigkeitsproportionale (viskose) Reibungskaft spüren würden.
Sie bewegen sich damit ganz ähnlich durch den Leiter wie Teilchen in einer
Flüssigkeit oder einem Gas.
3.4
Die elektrische Leistung eines Stromes an
einem Widerstand
Wir betrachten einen einfachen Stromkreis bestehend aus einer Spannungsquelle mit der Betriebsspanung U und einem Ohmschen Widerstand R, siehe Abb. 3.2. Die Spannung am Widerstand beträgt U = ϕ(a) − ϕ(b), wobei
ϕ(a) das elektrische Potential in Stromrichtung vor dem Widerstand und ϕ(b)
das elektrische Potential hinter dem Widerstand ist. Bewegt sich in Folge des
3.4 Die elektrische Leistung eines Stromes an einem Widerstand
57
Abbildung 3.2: Zur Berechnung der Leistung, die von einem Strom an einem
Widerstand abgeführt wird.
Stroms I in der Zeit dt die Ladung dQ = I dt durch den Widerstand R, so
verliert sie die potentielle Energie
dEp = dQ ϕ(b) − dQ ϕ(a) = − (ϕ(a) − ϕ(b)) dQ
= −U dQ = −U I dt .
Diese frei gewordene potentielle Energie entspricht gerade der Arbeit
dW = −dEp , die notwendig ist, um die Ladung dQ gegen die Reibungskraft“in
”
Gl. (3.16) durch den Leiter zu bewegen. Dabei wird folgende Leistung an dem
Widerstand R abgeführt.
P =
dW
dEp
=−
=UI .
dt
dt
(3.17)
Auf mikroskopischer Betrachtungsebene stellt sich der Vorgang folgendermaßen dar: Die Ladungsträger verlieren ihre potentielle Energie durch Stöße mit
den Gitter-Ionen des Leiters, die dadurch in Schwingungen versetzt werden.
Dabei erhöht sich die mittlere kinetische Energie der Ionen und damit die
Temperatur des Leiters. Letztlich wird die von den Ladungsträgern abgegebene Energie also in Wärme umgewandelt. Mit dem OHMschen Gesetz U = R I
und mit Gl. (3.17) läßt sich die an einem Widerstand R abgeführte Leistung
auch schreiben in der Form
P = I2 R =
U2
.
R
(3.18)
58
3.5
3 Der elektrische Strom
Die KIRCHHOFFschen Regeln
Üblicher Weise definiert man die Stromrichtung als positiv, in die sich positive
Ladungsträger bewegen würden, also von der positiven zur negativen Klemme
einer Batterie (technische Stromrichtung). Wir betrachten nun das Linienin~ entlang eines geschlossenen Stromkreises
tegral der elektrischen Feldstärke E
(bzw. einer Masche in einem Netzwerk). Dieses muss nach Gl. (1.18) verschwinden,
I
~ d~r = 0 .
E
(3.19)
C
Berücksichtig man, dass
U = ϕ(a) − ϕ(b) =
Zb
~ d~r
E
(3.20)
a
der Spannungsabfall über einem Bauelement ist, wobei ϕ(a) das elektrische
Potential vor dem Bauelement und ϕ(b) das elektrische Potential hinter dem
Bauelement bezeichnet, so folgt aus Gl. (3.19) direkt die KIRCHHOFFsche
Maschenregel:
In einem geschlossenen Stromkreis ist die Summe der Spannungen
Un über allen Bauelemente gleich Null, in Zeichen:
X
Un = 0 .
(3.21)
n
Die Spannungen (Potentialdifferenzen) Un an den Bauelementen entsprechen
Differenzen der potentiellen Energie einer Probeladung, siehe Gl. (1.17). Damit
drückt Gl. (3.21) letztlich eine Energieerhaltung aus. Führt man eine Probeladung einmal in einem geschlossene Stromkreis herum, so hat sie dieselbe
Energie wie am Anfang.
Als Beispiel sehen wir uns einen einfachen Stromkreis an, bestehend aus
einer Spannungsquelle mit der Betriebsspannug U und zwei Widerständen R1
und R2 , siehe Abb. 3.3. Offensichtlich gilt in Einklang mit der KIRCHHOFFschen Maschenregel
(ϕ(a) − ϕ(b)) + (ϕ(b) − ϕ(c)) + (ϕ(c) − ϕ(a)) = 0 ,
(3.22)
wobei ϕ(a), ϕ(b) und ϕ(c) die elektrischen Potentiale an den Punkten a, b und
c sind, siehe Abb. 3.3. Da U1 = ϕ(a) − ϕ(b) die Spannung am Widerstand R1 ,
59
3.5 Die KIRCHHOFFschen Regeln
Abbildung 3.3: Beispiel zur Anwendung der KIRCHHOFFschen Maschenregel.
U2 = ϕ(b) − ϕ(c) die Spannung am Widerstand R2 und U = ϕ(a) − ϕ(c) die
Betriebsspannung der Spannungsquelle ist, folgt aus Gl. (3.22)
U1 + U2 − U = 0 .
Wir haben demzufolge bei der Anwendung der KIRCHHOFFschen Maschenregel die Spannung über einem Bauelement mit einem positiven Vorzeichen
zu berücksichtigen, wenn wir beim Durchlauf der Masche erst auf das höhere
Potential (+) und dann auf das niedrigere Potential (-) stoßen. Entsprechend
haben wir die Spannung über einem Bauelement mit einem negativen Vorzeichen zu berücksichtigen, wenn wir erst auf das niedrigere Potential (-) und dann
auf das höhere Potential (+) stoßen. Die Betriebsspannung U muss demzufolge in dem Stromkreis in Abb. 3.3, wenn wir ihn in technischer Stromrichtung
durchlaufen, mit einem negativen Vorzeichen berüchsichtigt werden.
An einem Punkt, wo mehrere Leitungen in einem Netzwerk zusammentreffen gilt außerdem die KIRCHHOFFsche Knotenregel:
Die Summe aller Ströme In , die in einen Knoten hinein- und herausfließen, ist gleich Null, in Zeichen:
X
In = 0 .
(3.23)
n
Die KIRCHHOFFsche Knotenregel ist eine direkte Folgerung der Ladungserhaltung, siehe Gl. (3.8). In Gl. (3.23) müssen zu- und abfließende Ströme
mit entgegengesetzten Vorzeichen berücksichtigt werden. Häufig ordnet man
willkürlich den abfließenden Strömen ein negatives und den zufließenden
Strömen ein positives Vorzeichen zu.
60
3 Der elektrische Strom
Auch hierzu betrachten wir ein kleines Beispiel. Für den Knoten in Abb. 3.4
gilt mit der KIRCHHOFFschen Maschenregel
I1 − I2 − I3 = 0 ,
bzw.
I1 = I2 + I3 .
Abbildung 3.4: Beispiel zur Anwendung der KIRCHHOFFschen Knotenregel.
Als weitere Anwendung der KIRCHHOFFschen Regeln betrachten wir die
Reihen- und Parallelschaltung von Ohmschen Widerständen, siehe Abb. 3.5.
Für die Reihenschaltung zweier Widerstände R1 und R2 (Abb. 3.5a) gilt nach
der KIRCHHOFFschen Maschenregel
U = U1 + U2 ,
wobei U1 die Spannung am Widerstand R1 und und U2 die Spannung am
Widerstand R2 ist. Mit I = I1 = I2 , wobei I1 der Strom durch den Widerstand
R1 und und I2 der Strom durch den Widerstand R2 ist, folgt
U = R1 I + R2 I = (R1 + R2 ) I .
Durch Vergleich mit dem OHMschen Gesetz U = R I folgt für den Gesamtwiderstand R einer Reihenschaltung zweier Widerstände R1 und R2
R = R1 + R2 .
Für die Parallelschaltung zweier Widerstände R1 und R2 (Abb. 3.5b) gilt
nach der KIRCHHOFFschen Knotenregel
I = I1 + I2 ,
61
3.5 Die KIRCHHOFFschen Regeln
Abbildung 3.5: Reihenschaltung (a) und Parallelschaltung (b) zweier Widerstände.
wobei I1 der Strom durch den Widerstand R1 und und I2 der Strom durch den
Widerstand R2 ist. Mit U = U1 = U2 , wobei U1 die Spannung am Widerstand
R1 und und U2 die Spannung am Widerstand R2 ist, folgt
U
U
1
1
I=
+
=
+
R1 R2
R1 R2
U .
Durch Vergleich mit dem OHMschen Gesetz I = U/R folgt für den Gesamtwiderstand R einer Parallelschaltung zweier Widerstände R1 und R2
1
1
1
=
+
.
R
R1 R2
62
3 Der elektrische Strom
Kapitel 4
Das magnetische Feld
4.1
Kräfte auf bewegte Ladungen im Magnetfeld
Magnetfelder werden hervorgerufen durch elektrische Ströme aber auch durch
Permanentmagneten wie Hufeisen- und Stabmagneten. Die Feldlinien sind
stets geschlossen. Bei einem Stab- oder Hufeisenmagneten bezeichnet man den
Pol, wo die Feldlinien austreten als Nordpol, und den Pol, wo sie eintreten als
Südpol. Man kann das Vorhandensein eines Magnetfeldes durch Eisenfeilspäne
oder Kompassnadeln sichtbar machen. Magnetfelder erzeugen aber auch eine
Kraft auf bewegte elektrische Ladungen. Wir betrachten dazu die Anordnung
in Abb. (4.1). Eine Ladung q bewege sich mit der Geschwindigkeit ~v durch ein
~ Dann wirkt auf sie die LORENTZ-Kraft:
homogenes Magnetfeld B.
~ .
F~ = q (~v × B)
(4.1)
Abbildung 4.1: Kraft auf eine bewegte elektrische Ladung im Magnetfeld.
63
64
4 Das magnetische Feld
~ Gilt
Die LORENTZ-Kraft steht also senkrecht auf den Vektoren ~v und B.
~
speziell ~v ⊥ B, so folgt aus Gl. (4.1) für den Betrag der LORENTZ-Kraft
F = qvB .
(4.2)
Die Einheit Tesla (T) des Magnetfeldes ergibt sich aus dieser Gleichung zu
T=
Ns
.
Cm
Außerdem wird noch die Einheit 1 Gauß (G) verwendet, für die gilt
1 G = 10−4 T.
Hängen wir, wie in Abb. 4.2 dargestellt, einen stromdurchflossenen Leiter in
ein Magnetfeld, so erfahren die Ladungsträger in dem Leiter gemäß Gl. (4.1)
eine Kraft, und damit erfährt auch der gesamte Leiter eine Kraft, die wir nun
berechnen wollen. Für den Strom in dem Leiter gilt zunächst
I = j A = nqvA ,
(4.3)
wobei n die Ladungsträgerdichte, q die Ladung der Ladungsträger, v die Driftgeschwindigkeit der Elektronen und A die Querschnittsfläche des Leiters be~ so erhält man mit
zeichnet. Ist l die Länge des Leiters im Magnetfeld B,
Gl. (4.1) für die Kraft auf den Leiter
~
F~ = l A n q (~v × B)
bzw. mit Gl. (4.3)
~ .
F~ = I (~l × B)
(4.4)
Abbildung 4.2: Kraft auf einen geradlinigen, stomdurchflossenen Leiter im
Magnetfeld.
4.1 Kräfte auf bewegte Ladungen im Magnetfeld
65
Hierbei gibt der Vektor ~l die Länge des Leiters an und zeigt in Richtung von
~v , bzw. in Richtung des Stroms.
Für das Magnetfeld eines langen Drahtes zeigt sich experimentell, dass die
magnetischen Feldlinien den Draht konzentrisch umschließen, siehe Abb. 4.3,
und für den Betrag des Magnetfeldes gilt
B=
µ0 I
.
2π r
(4.5)
Der Betrag des Magnetfeldes ist also proportional zu I und umgekehrt proportional zu dem Abstand r von der Drahtachse. Die Richtung des Magnetfeldes
und Stromes stehen in einem Rechtsschraubensinn zueinander.
Abbildung 4.3: Das Magnetfeld eines langen, geradlinigen stromdurchlossenen
Drahtes.
Als nächstes betrachten wir zwei unendlich lange, parallele, stromdurchflossene Leiter, die in einem Abstand r voneinander angeornet sind, siehe Abb. 4.4.
Der Strom habe in beiden Leitern denselben Wert I und soll in beiden Leitern
in die gleiche Richtung fließen . Die Länge l der Leiter sei sehr groß gegenüber
dem Abstand r (l ≫ r), so dass wir Randeffekte vernachlässigen können. Wir
wollen die Kraft berechnen, mit der sich beide Drähte anziehen. Der Strom
I in einem der Leiter, z.B. dem linken, erzeugt am Ort des rechten Leiters
~ mit einem Betrag gemäß Gl. (4.5). Dieses Magnetfeld steht
ein Magnetfeld B
überall senkrecht auf dem rechten Leiter. Es übt somit gemäß Gl. (4.4) auf
den rechten Leiter eine Kraft F~ aus mit dem Betrag
F = lI B ,
die, wie Abb. 4.4 dargestellt ist, nach links gerichtet ist. Setzt man B aus
Gl. (4.5) in diese Beziehung ein, so folgt für die Kraft, die der linke Draht auf
66
4 Das magnetische Feld
Abbildung 4.4: Kraft zwischen zwei unendlich langen, stromdurchlossenen Leitern.
den rechten ausübt:
µ0 I 2
.
(4.6)
2π r
Der rechte Draht übt auf den linken eine entgegengesetzt gerichtete, vom Betrage gleich große Kraft aus. Beide Drähte ziehen sich also mit der obigen Kraft
an. Aus Gl. (4.6) erhalten wir für die Kraft pro Längeneinheit
F =l
µ0 I 2
F
=
.
l
2π r
(4.7)
Diese Gleichung ist von großer Bedeutung in der Elektrizitätslehre, denn mit
ihr wird die Einheit der Stromstärke, das Ampere (A) definiert, und die Festlegung aller weiteren Einheiten wird dann daraus abgeleitet. Die magnetische
Feldkonstante µ0 wird festgesetzt auf den Wert
µ0 = 4 π · 10−7
N
.
A2
(4.8)
Das führt mit Gl. (4.7) zu folgender Definition der Einheit der Stromstärke:
Ein Ampere ist die Stärke eines Stroms, der durch zwei im Vakuum parallel im Abstand 1 m voneinander angeordnete, geradlinige, unendlich lange Leiter fließt und zwischen diesen Leitern pro
Längeneinheit eine Kraft von 2 · 10−7 N hervorruft.
67
4.2 Das BIOT-SAVARTsche Gesetz
Aus der Definition des elektrischen Stroms I = dQ/dt ergibt sich damit für die
Definition der Einheit der Ladung:
Die Ladung 1 Coulomb (C) ist definiert als die Ladung, die in einer
Sekunde durch die Querschnittsfläche eines Leiters transportiert
wird, in dem der konstante Strom 1 Ampere fließt. Also C = A s.
Aus der Definitionsgleichung für das elektrische Potential (1.17) folgt für die
Einheit der Spannung (Volt) V = J/C, und aus der Defenitionsgleichung für
den elektrische Widerstand (3.9) folgt für die Einheit des Widerstandes (Ohm)
Ω = V/A.
4.2
Das BIOT-SAVARTsche Gesetz
Wir haben im vorigen Abschnitt gesehen, dass für einen unendlich langen,
~ konzentrische Kreise um
geradlinigen Leiter die Feldlinien des Magnetfeldes B
~
den Leiter bilden, und dass für den Betrag von B gilt:
B=
µ0 I
.
2π r
(4.9)
Obiges Gesetz ist ein Spezialfall des allgemeineren Gesetzes von BIOT und
SAVART, welches die Berechnung des Magnetfeldes für eine beliebige Stromverteilung erlaubt. Es lautet in differentieller Form
~ =
dB
µ0 I d~l × ~ˆr
.
4π
r2
(4.10)
~ der Anteil des Magnetfeldes, der von dem Leiterelement d~l erDabei ist dB
zeugt wird, siehe Abb. 4.5. Der Vektor ~r zeigt von dem Leiterelement zu dem
Aufpunkt P , in dem das Magnetfeld berechnet werden soll. Der Vektor ~ˆr ist der
zugehörige Einheitsvektor und I bezeichnet den Strom, der in dem Leiter fließt.
~ steht nach Gl. (4.10) senkrecht auf d~l und ~r und hängt
Das Magnetfeld dB
somit mit der Richtung des Stroms über einem Rechtsschraubensinn zusam~ eines stromdurchflossenen Leiters
men. Will man das gesamte Magnetfeld B
haben, so muss man längs des Leiters integrieren, und erhält aus Gl. (4.10)
das BIOT-SAVARTsche Gesetz in Integralform:
~ =
B
Z
C
µ0 I d~l × ~ˆr
.
4π
r2
(4.11)
68
4 Das magnetische Feld
Abbildung 4.5: Das von einem infinitesimalen Leiterelement d~l erzeugte Ma~
gnetfeld dB.
Als Beispiel soll das Magnetfeld eines unendlich langen, geradlinigen Leites
berechnet werden, siehe Abb. 4.6. Wir wollen das Magnetfeld bestimmen in
einem beliebigen Punkt, der den Abstand R von dem Leiter habe. Der Leiter
liege auf der x-Achse des verwendeten Koordinatensystems. Für das Leiterelement d~l gilt damit d~l = dx ~ex , wobei ~ex der Einheitsvektor in x-Richtung ist.
Wegen des Kreuzpoduktes in Gl. (4.10) ergibt sich sofort, dass das Magnetfeld
in Abb. 4.6 aus der Zeichenebene herauszeigt. Für den Betrag dB des von dem
Leiterelement dx erzeugten Magnetfeldes folgt aus Gl. (4.10) mit r2 = x2 + R2
dB =
µ0 I dx sin θ
µ0
I R dx
.
=
2
2
4π x + R
4 π (x2 + R2 ) 23
Hierbei ist θ der von d~l und ~r eingeschossene Winkel. Für den Sinus dieses Winkels kann man aus Abb. 4.6 die Beziehung sin θ = sin(π − θ) = R/(x2 + R2 )1/2
ablesen, die wir bei der zweiten Gleichheit verwendet haben. Das Magnetfeld
des gesamten Leiter erhalten wir nun durch Integration entlang der gesamten
x-Achse von −∞ bis ∞, also
B =
Z∞
−∞
µ0
I R dx
4 π (x2 + R2 ) 23
∞
dx
µ0 I R Z
=
3
4π
(x2 + R2 ) 2
−∞
69
4.3 Das GAUSSsche Gesetz für das Magnetfeld
µ0 I R
=
4π
"
x
1
R2 (x2 + R2 ) 2
µ0 I R 2
=
,
4 π R2
und damit
B=
#∞
−∞
(4.12)
µ0 I
,
2π R
in Übereinstimmung mit dem uns bereits bekannten Resultat in Gl. (4.9). Das
Magnetfeld in Gl. (4.9) stellt also, wie bereits erwähnt, einen Spezialfall des
wesentlich allgemeineren BIOT-SAVARTschen Gesetzes dar.
Abbildung 4.6: Zur Berechnung des Magnetfelds eines unendlich langen, geradlinigen stromdurchlossenen Leiters.
4.3
Das GAUSSsche Gesetz für das Magnetfeld
Wir wollen in diesem Abschnitt das GAUSSsche Gesetz für das Magnetfeld
~
formulieren. Wir betrachten dazu den Fluss Φ des magnetischen Feldes B
durch eine Fläche A,
Z
~ dA
~ .
Φ= B
(4.13)
A
Der magnetische Fluss Φ wird im Zusammenhang mit dem Phänomen der Induktion noch eine sehr wichtige Rolle spielen, siehe Kap. 5. Er wird in der Einheit Weber (Wb) gemessen. Nach Gl. (4.13) gilt Wb = T · m2 . Das GAUSSsche
Gesetz lautet nun:
70
4 Das magnetische Feld
~ durch eine beliebige geschlossenen
Der Fluss des Magnetfeldes B
Fläche A ist stets gleich Null, in Zeichen:
I
~ dA
~=0 .
B
(4.14)
A
Man kann dies auch so formulieren: Das Magnetfeld ist quellen”
frei“.
Das GAUSSsche Gesetz kann allgemein aus dem BIOT-SAVARTschen Gesetz hergeleitet werden. Wir gehen bei unserer Herleitung der Einfachheit halber von dem Magnetfeld eines unendlich langen, geradlinigen, stromdurchflossenen Leiters aus, welches in Abb. 4.3 dargestellt ist, und dessen Betrag gemäß
Gl. (4.5) gegeben ist durch
µ0 I
B=
.
(4.15)
2π r
Wir berechnen zunächst den Fluss dieses Magnetfelds durch eine spezielle
geschlossenen Fläche, nämlich die Oberfläche eines Zylindersegments, wie in
Abb. 4.7 dargestellt. Da die Feldlinien konzentrische Kreise um den Leiter
bilden, und der Betrag des Magnetfeldes entlang dieser Kreise konstant ist,
kann man aus Abb. 4.7 direkt ablesen, dass der Fluss durch die Fläche A1
entgegengesetzt gleich groß dem Fluss durch die Flächa A2 ist. Diese beiden
~ eines unendlich langen, geradliniAbbildung 4.7: Der Fluss des Magnetfeld B
gen, stromdurchflossenen Leiters durch die Oberfläche eines Zylindersegments.
4.3 Das GAUSSsche Gesetz für das Magnetfeld
71
Anteile zum Fluss des Magnetfeldes durch die gesamte, geschlossenen Oberfläche des Zylindersegments heben sich somit gegenseitig auf. Der Fluss durch
alle übrigen Flächen des Zylindersegments verschwinden, da das Magnetfeld
~ tangential zu diesen Flächen liegt, bzw. B
~ in diesen Flächen senkrecht auf
B
~ steht. Damit ist der Fluss des Magnetfeldes durch
den Flächenelementen dA
die gesamte Oberfläche gleich Null.
Nun wollen wir den Fluss durch eine beliebig geformte, geschlossene Oberfläche A berechnen. Eine beliebige Oberfläche kann aber durch eine Überlagerung geeigneter Zylindersegmente aufgebaut werden, wie in Abb. 4.8 dargestellt. Dabei wird die Oberfläche A beliebig genau approximiert durch kleine,
konzentrische Zylinderflächensegmente, die verbunden sind durch kleine, radial gerichtete, ebene Flächenstücke. Die Anteile zum Flussintegral in Gl. (4.14)
~
durch die Zylinderflächensegmente verschwinden alle, da das Magnetfeld B
tangential zu diesen Flächen liegt. Die Anteile durch die planaren, radial verlaufenden Seitenflächen, z.B. durch die Flächen A1 und A2 in Abb. 4.8, heben
sich paarweise auf, ganz ähnlich wie bei der in Abb. 4.7 dargestellten Konfiguration. Damit ist die Beziehung in Gl. (4.14) aber für beliebige geschlossene
Flächen im Magnetfeld eines geraden Leites bewiesen. Auf Grund des Superpositionsprinzips und wegen der Linearität des Integrals lässt sich diese Be-
~ eines unendlich langen, geradliAbbildung 4.8: Der Fluss des Magnetfeldes B
nigen, stromdurchflossenen Leiters durch eine beliebige Oberfläche. Der Leiter
steht senkrecht zur Zeichenebene, der Strom ist aus der Zeichenebene heraus
gerichtet.
72
4 Das magnetische Feld
ziehung auch auf das Magnetfeld einer beliebigen Anordnung von geradlinigen
Leitern verallgemeinern, und schließlich, was hier nicht mehr bewiesen werden
soll, auch auf das Magnetfeld beliebiger Stromverteilungen oder Permanentmagnete.
4.4
Das AMPEREsche Gesetz
Wir wollen in diesem Kapitel das AMPEREsche Gesetz herleiten. Es lautet:
~ gilt: Das Integral
Für ein beliebiges statisches Magnetfeldes B
des Magnetfeldes längs einer beliebigen geschlossenen Kurve C ist
gleich dem gesamten Strom I, der von dieser Kurve umschlossen
wird, multipliziert mit µ0 , in Zeichen
I
~ d~r = µ0 I .
B
(4.16)
C
Das AMPEREsche Gesetz kann allgemein aus dem BIOT-SAVARTschen
Gesetz hergeleitet werden. Wir gehen bei unserer Herleitung der Einfachheit
halber wieder von dem Magnetfeld eines unendlich langen, geradlinigen, stromdurchflossenen Leiters aus,
µ0 I
,
(4.17)
B=
2π r
und berechnen zunächst das Integral dieses Magnetfelds entlang einer bestimmten, geschlossenen Kurve C, die den Leiter nicht umschließt, siehe Abb. 4.9.
Die Kurve bestehe aus den beiden Kreisbögen C1 und C2 , die durch zwei geradlinige, radial verlaufende Wegstücke C3 und C4 verbunden sind. Die gesamte
Kurve werde im Gegenuhrzeigersinn durchlaufen. Die Intergrale längs der geradlinigen Wegstücke C3 und C4 tragen zu dem gesamten Kurvenintegral in
~ senkrecht auf diesen Wegstücken
Gl. (4.16) nichts bei, da das Magnetfeld B
steht, also
Z
Z
~
~ d~r = 0 .
B d~r = B
(4.18)
C3
C4
Für die Integrale entlang der Kreisbögen folgt mit Gl. (4.17)
Z
C1
bzw.
~ d~r = − B1 s1 = − µ0 I s1
B
2 π r1
(4.19)
~ d~r = B2 s2 = µ0 I s2 .
B
2 π r2
(4.20)
Z
C2
73
4.4 Das AMPEREsche Gesetz
Abbildung 4.9: Zur Berechnung des Integrals in Gl. (4.16) entlang einer speziellen geschlossenen Kurve, die den geradlinigen, stromdurchflossenen Leiter
nicht umschließt. Sie besteht aus den beiden Kreisbögen C1 und C2 , die durch
zwei geradlinige, radial verlaufende Wegstücke C3 und C4 verbunden sind.
Dabei bezeichet B1 den Betrag des Magnetfeldes entlang des inneren Kreisbogens, s1 die Länge und r1 den Radius des inneren Kreisbogens, sowie B2 den
Betrag des Magnetfeldes entlang des äußeren Kreisbogens, s2 die Länge und r2
den Radius des äußeren Kreisbogens. Da beide Kreisbögen durch die gleichen,
radial verlaufenden Geraden begrenzt werden, die den Winkel θ einschließen,
gilt s1 = r1 θ und s2 = r2 θ, und damit s2 = (r2 /r1 ) s1 . Damit folgt aus den
Gln. (4.19) und (4.20)
Z
Z
~ d~r .
~ d~r = − B
(4.21)
B
C2
C1
Aus den Gln. (4.18) und (4.21) folgt schließlich, dass das Integral längs des
gesamten geschlossenen Weges C = C1 + C2 + C3 + C4 in Abb. 4.9 gleich Null
ist.
Wir betrachten nun eine beliebige geschlossene Kurve C, die den Leiter nicht
umschließt, und berechnen das Integral des Magnetfeldes entlang dieser Kurve.
Wie in Abb. 4.10 dargestellt, kann eine beliebige geschlossene Kurve C beliebig
genau approximiert werden durch kleine konzentrische Kreisbögen, die durch
kleine radial verlaufende, geradlinige Wegstücke verbunden sind. Die Anteile
74
4 Das magnetische Feld
zum Kurvenintegral entlang der geradlinigen Wegstücke verschwinden, da das
~ senkrecht auf diesen Wegstücken steht. Die Anteile entlang der
Magnetfeld B
Kreisbögen, z.B. entlang C1 und C2 in Abb. 4.10, heben sich paarweise auf,
ganz ähnlich wie bei der in Abb. 4.9 dargestellten Konfiguration. Damit haben
wir gezeigt, dass das Integral des Magnetfeldes eines geradlinigen Leiters entlang einer beliebigen, geschlossenen Kurve C, die den Leiter nicht umschließt,
gleich Null ist.
Abbildung 4.10: Zur Berechnung des Integrals in Gl. (4.16) entlang einer beliebigen geschlossenen Kurve C, die den geradlinigen, stromdurchflossenen Leiter
nicht umschließt.
Wir betrachten nun das Integral des Magnetfeldes eines geradlinigen Leiters
entlang einer speziellen, geschlossenen Kurve C, die den Leiter umschließt.
Dieser Weg sei ein Kreis mit dem Radius r, durch dessen Mittelpunkt der
Leiter senkrecht zur Kreisfläche verläuft, siehe Abb. 4.11. Die Richtung des
Stromes zeige senkrecht aus der Zeichenebene heraus. Der Kreis werde im
Gegenuhrzeigersinn durchlaufen. Mit Gl. (4.17) folgt
I
C
~ d~r = µ0 I 2πr = µ0 I .
B
2π r
(4.22)
Aus obiger Betrachtung ergibt sich sofort, dass in Gl. (4.22) der Strom I positiv gezählt wird, wenn er in einem Rechtsschraubensinn von der Kurve C
umschlossen wird, andernfalls wird er negativ gezählt.
4.4 Das AMPEREsche Gesetz
75
Abbildung 4.11: Zur Berechnung des Integrals in Gl. (4.16) entlang einer
kreisförmigen Kurve mit dem Radius r, die den geradlinigen, stromdurchflossenen Leiter symmetrisch umschließt.
Der Sachverhalt in Gl. (4.22) läßt sich direkt übertragen auf beliebige, geschlossene Kurven, die den Leiter umschießen. Eine beliebige, geschlossene
Kurve C läßt sich nämlich, wie in Abb. 4.12 dargestellt, beliebig genau approximieren durch konzentrische Kreisbögen, die durch kleine radial verlaufende, geradlinige Wegstücke verbunden sind. Die Anteile zum Kurvenintegral
~ senkentlang der geradlinigen Wegstücke verschwinden, da das Magnetfeld B
recht auf diesen Wegstücken steht. Die Anteile auf den weiter außen liegenden
Abbildung 4.12: Zur Berechnung des Integrals in Gl. (4.16) entlang einer beliebeigen Kurve C, die den geradlinigen, stromdurchflossenen Leiter umschließt.
76
4 Das magnetische Feld
Kreisbögen können direkt in Beziehung gesetzt werden, mit entsprechenden
Anteilen auf einem weiter innen liegenden Kreis. Zum Beispiel gilt für die
beiden Kreisbogensegmente C2 und C1 in Abb. 4.12
Z
~ d~r = B2 s2 = µ0 I s2
B
2 π r2
(4.23)
Z
~ d~r = B1 s1 = µ0 I s1 .
B
2 π r1
(4.24)
C2
bzw.
C1
Dabei bezeichet B1 den Betrag des Magnetfeldes entlang des inneren Kreisbogens, s1 die Länge und r1 den Radius des inneren Kreisbogens, sowie B2 den
Betrag des Magnetfeldes entlang des äußeren Kreisbogens, s2 die Länge und r2
den Radius des äußeren Kreisbogens. Da beide Kreisbögen durch die gleichen,
redial verlaufenden Geraden begrenzt werden, die den Winkel θ einschließen,
gilt s1 = r1 θ und s2 = r2 θ, und damit s2 = (r2 /r1 ) s1 . Damit folgt aus den
Gln. (4.23) und (4.24)
Z
Z
~ d~r .
~
B d~r = B
C1
C2
Summiert man nun über alle die Kurve C approximierenden Kreisbögen auf,
so zeigt sich, dass das Kurvenintegral längs der geschlossenen Kurve C gleich
ist dem Kurvenintegral längs des weiter innen liegenden Kreises. Für dieses gilt
aber Gl. (4.22). Damit haben wir aber gezeigt, dass für das Kurvenintegral des
~ eines geradlinigen Leiters längs eines beliebigen, geschlossenen
Magnetfeldes B
Weges C, der den Leiter umschließt, gilt
I
~ d~r = µ0 I .
B
C
Auf Grund des Superpositionsprinzips und wegen der Linearität des Integrals lässt sich dieser Sachverhalt auch auf das Magnetfeld einer beliebigen
Anordnung von geradlinigen Leitern verallgemeinern. Für die in Abb. 4.13
dargestellte Anordnung gilt beispielsweise
I
C
~ d~r = µ0 (I1 + I2 − I3 ) .
B
(4.25)
Dabei müssen, wie oben erwähnt, die Ströme, die im Rechtsschraubensinn
von der Kurve C umschlossen werden (z.B. I1 und I2 in Abb. 4.13), positiv
gezählt werden, während die übrigen (z.B. I3 in Abb. 4.13) negativ zu zählen
4.4 Das AMPEREsche Gesetz
77
Abbildung 4.13: Zur Berechnung des Integrals in Gl. (4.16) entlang einer beliebigen Kurve C für den Fall eines Magnetfeldes einer Anordnung bestehend
aus mehreren geradlinigen Leitern.
sind. Die Ströme I4 und I5 tauchen auf der rechten Seite von Gl. (4.25) nicht
auf, da sie von der Kurve C nicht umschlosen werden. Schließlich kann man
noch zeigen, dass Gl. (4.25) auch für beliebig geformte Leiter gilt. Damit ist
das AMPEREsche Gesetz bewiesen. Es sei noch einmal ausdrücklich darauf
~ in
hingewiesen, dass in dem AMPEREschen Gesetz (4.16) das Magnetfeld B
dem Kurvenintegral das Feld ist, das von allen Strömen herrührt, sowohl die
innerhalb, als auch die außerhalb der geschlossenen Kurve liegen, während I
auf der rechten Seite der Gl. (4.16) nur die Ströme umfasst, die von der Kurve
umschlossen werden. Außerdem sei angemerkt, dass das AMPEREsche Gesetz
nur im Rahmen der Magnetostatik, also für Magnetfelder konstanter Ströme
gilt. Bei zeitlich veränderlichen Strömen erfährt das AMPEREsche Gesetz eine
Erweiterung, auf die wir später zu sprechen kommen
Wir wollen nun einige Anwendungen des AMPEREschen Gesetzes betrachten. Als erstes wollen wir das Magnetfeld eines langen geradlinigen Leiters
berechnen, durch den der Strom I fließt. Der Draht habe in diesem Fall den
endlichen Radius a, und wir wollen das Magnetfeld sowohl außerhalb, als auch
im Innern des Drahtes berechnen, siehe Abb. 4.14. Für die Anwendung des
AMPEREschen Gesetzes verwenden wir einen kreisförmigen Integrationsweg,
dessen Mittelpunkt mit der Symmetrieachse des Drahtes zusammenfällt. Aus
Symmetriegründen kann das Magnetfeld nur vom Abstand r von der Symmetrieachse abhängen. Es kann keine radiale Komponente haben, da sich dann
ein magnetischer Fluss durch geschlossene, den Draht symmetrisch umgebende
Zylinderflächen ergäbe, was dem GAUSSschen Gesetz Gl. (4.14) widersprechen
~ tangential zu dem Kreis. Wir wollen das
würde. Also liegt das Magnetfeld B
Magnetfeld zunächst im Außenraum berechnen, und wählen deshalb r > a
78
4 Das magnetische Feld
Abbildung 4.14: Zur Berechnung des Magnetfeldes außerhalb und innerhalb
eines stromdurchflossenen Drahtes.
(Fall 1 in Abb. 4.14). Das AMPEREsche Gesetz (4.16) liefert
B 2πr = µ0 I
und damit
µ0 I
für r > a .
(4.26)
2π r
Im Außenraum ist das Magnetfeld eines Drahtes mit endlichem Durchmesser
also identisch mit dem eines beliebig dünnen Drahtes, durch den der gleiche
Strom fließt, siehe Gl. (4.17). Um das Magnetfeld im Innern des Leiters zu berechnen, wählen wir für den Radius r des kreisförmigen Integrationsweges r < a
(Fall 2 in Abb. 4.14). Jetzt wird nicht mehr der komplette Strom I von dem
Integrationsweg umschlossen, sondern nur der Teil I (πr2 /πa2 ) = I (r2 /a2 ), wobei wir angenommen haben, dass die Stromdichte über dem ganzen, kreisförmigen Leiterquerschnitt konstant ist. Das AMPEREsche Gesetz liefert dann
B=
B 2πr = µ0 I
und damit
r2
,
a2
µ0 I r
für r < a .
(4.27)
2 π a2
Im Innenraum des Leiters nimmt das Magnetfeld also proportional mit r
zu, während es im Außenraum umgekehrt proportional zu r abfällt, siehe
Abb. 4.14.
B=
79
4.4 Das AMPEREsche Gesetz
Abbildung 4.15: Zur Berechnung des Magnetfeldes eines stromdurchflossenen
Koaxialkabels.
Als nächstes wollen wir das Magnetfeld eines Koaxialkabels berechnen, siehe Abb. 4.15. Das Koaxialkabel bestehe aus einem Innenleiter mit dem Radius
a und einem Außenleiter mit dem Radius b. In beiden Leitern fließt der Strom
I, aber in entgegengesetzte Richtung. Mit denselben Überlegungen wie im vorigen Abschnitt ergibt sich, dass das Magnetfeld nur vom Abstand r von der
Symmetrieachse abhängen kann, und keine Radialkomponente besitzen kann.
Als Integrationsweg wählen wir, die Symmetrie der Anordnung ausnutzend,
wieder einen Kreis, dessen Mittelpunkt mit der Symmetrieachse des Koaxialkabels zusamenfällt. Für r > b liefert das AMPEREsche Gesetz (4.16)
B 2πr = µ0 (I − I) ,
weil der Strom I im Innenleiter im Rechtsschraubensinn, der Strom I im Außenleiter aber in entgegengesetztem Sinn von dem Integrationsweg umschlossen
wird. Damit gilt B = 0 für r > b. D.h. im Außenraum des Koaxialkabels verschwindet das Magnetfeld. Legt man den kreisförmigen Integrationsweg zwischen die beiden Leiter, wählt also für den Radius r einen Wert in dem Bereich
a < r < b, so liefert das AMPEREsche Gesetz (4.16)
B 2πr = µ0 I
und damit
µ0 I
für a < r < b .
(4.28)
2π r
Im Zwischenraum zwischen den Leitern ist das Magnetfeld eines Koaxialkabels
also identisch mit dem eines beliebig dünnen Drahtes, siehe Gl. (4.17). Ist der
B=
80
4 Das magnetische Feld
Innenleiter ein Vollleiter, so ist das Magnetfeld in diesem durch Gl. (4.27)
gegeben, ist der Innenleiter ein Hohlleiter, so verschwindet das Magnetfeld in
seinem Inneren. Zur Begründung wähle man in Abb. 4.15 einen kreisförmigen
Integrationsweg mit r < a und wende das AMPEREsche an.
Als letztes wollen wir noch das Magnetfeld einer langen, dicht gewickelten
Spule berechnen, siehe Abb. 4.16. Ist die Länge der Spule sehr groß im Vergleich
zu ihrem Durchmesser, so kann das Magnetfeld im Innern der Spule als parallel zur Spulenachse orientiert und konstant angenommen werden, während
das Magnetfeld im Außenraum als vernachlässigbar klein angenommen werden kann. Für die Anwendung des AMPEREschen Gesetzes betrachten wir
das Integral des Magnetfeldes der Spule längs eines rechteckförmigen Integrationsweges C, bestehend aus den vier geraden Wegstücken C1 bis C4 , siehe
Abb. 4.16. Der Strom trete in den von dem Integrationsweg umschlossenen
Wicklungen aus der Zeichenebene heraus und wird so von dem im Gegenuhrzeigersinn durchlaufenen Integrationsweg in einem Rechtsschraubensinn umschlossen. Die Anteile zum Kurvenintegral längs der Wegstücke C2 und C4
verschwinden, da das Magnetfeld senkrecht auf diesen Wegstücken steht. Der
Anteil längs des Wegstückes C3 verschwindet ebenfalls, da im Außenraum der
~ = 0 gilt. Der Anteil längs des Wegstückes C1 liefert B L, da B
~ entlang
Spule B
des Wegstückes C1 konstant ist. Wendet man das AMPEREsche Gesetz (4.16)
nun auf den gesamten geschlossenen Integrationsweg C = C1 + C2 + C3 + C4
an, so folgt
B L = µ0 N I ,
wobei N die Anzahl der Windungen ist, die von dem Integrationsweg umschlossen werden, die also auf ein Spulenstück der Länge L entfallen. Damit
Abbildung 4.16: Zur Berechnung des Magnetfeldes einer langen Spule.
4.5 Drehmoment auf eine Leiterschleife im Magnetfeld
81
folgt
B = µ0
N
I = µ0 n I ,
L
(4.29)
wobei n = N/L die Wicklungsdichte der Spule ist, also die Anzahl der Wicklungen pro Längeneinheit. Da der rechteckförmige Integrationsweg in Abb. 4.16
beliebig durch das Spuleninnere gelegt werden kann, ohne dass sich an dem Resultat in Gl. (4.29) etwas ändert, folgt, dass das Magnetfeld im Spuleninneren
homogen ist und durch Gl. (4.29) gegeben ist.
4.5
Drehmoment auf eine Leiterschleife im
Magnetfeld
In Kap. 4.1 Gl. (4.4) hatten wir gesehen, dass die Kraft auf einen geradlinigen,
~ gegeben ist durch
stromdurchflossenen Leiter der Länge l in eine Magnetfeld B
~ ,
F~ = I (~l × B)
(4.30)
wobei I die Stromstärke in dem Leiter bezeichnet, und der Vektor ~l zeigt von
dem einen Ende des Leiters zum anderen und ist in Richtung des Stromes
orientiert ist. Die Kraft in Gl. (4.30) liegt fast allen elektrischen Maschinen zu
Grunde.
Als Beispiel betrachten wir eine rechteckförmige Leiterschleife in einem Ma~ Sie sei um eine Achse drehbar gelagert und führe den Strom I,
gnetfeld B.
siehe Abb. 4.17. Die Längenabmessungen der Leiterschleife sein a und b. Bei
~ beziehen wir uns auf das
der folgenden Berechnung des Drehmomentes M
Schnittbild in Abb. 4.18. Zum Drehmonent um die Drahtachse tragen nur die
beiden Kräfte F~1 und F~2 bei, die jeweils auf die geradlinigen Leiterstücke der
Länge b wirken. Die Kräfte Kräfte F~1 und F~2 sind entgegengesetzt gerichtet,
und haben gemäß Gl. (4.30) beide den Betrag
F1 = F2 = I b B .
(4.31)
Der Vektor ~r1 in Abb. 4.18 bezeichnet den Ortsvektor (Hebelarm), der von
der Drehachse zum Angriffspunkt der Kraft F~1 zeigt. Analog bezeichnet ~r2
den Ortsvektor (Hebelarm), der von der Drehachse zum Angriffspunkt der
Kraft F~2 zeigt. Wegen ~r2 = −~r1 und F~2 = −F~1 folgt für die von den Kräften
~ 1 = ~r1 × F~1 bzw. M
~ 2 = ~r2 × F~2 , dass
F~1 bzw. F~2 ausgeübten Drehmomente M
~
~
~
gilt M2 = M1 . Der Hebelarm ~r1 und die Kraft F1 schließen den Winkel ϑ ein,
82
4 Das magnetische Feld
Abbildung 4.17: Drehmoment auf eine Leiterschleife im Magnetfeld.
ebenso der Hebelarm ~r2 und die Kraft F~2 . Mit Gl. (4.31) ergibt sich damit für
~ 1 und M
~2
den Betrag der Drehmomente M
M1 = M2 =
a
I b B sin ϑ .
2
Abbildung 4.18: Zur Berechnung des Drehmoments auf eine Leiterschleife im
Magnetfeld.
83
4.6 Der HALL-Effekt
~ =M
~1 +M
~2
Damit folgt für den Betrag des gesamten Drehmoments M
M = I a b B sin ϑ = I A B sin ϑ ,
(4.32)
wobei A = a b die Fläche der rechteckförmigen Leiterschleife bezeichnet. Wir
führen nun das magnetische Dipolmoment m
~ einer Leiterschleife ein:
~ .
m
~ =IA
(4.33)
~ so orientiert, dass er senkrecht auf der LeiterDabei ist der Flächenvektor A
schleife steht und mit der Richtung des Stroms I in einem Rechtsschraubensinn
verbunden ist. Sein Betrag gibt die Größe der von der Leiterschleife umrandeten Fläche an. Für die rechteckförmige Leiterschleife in Abb. 4.17 gilt damit
~ und
A = a b. Aus Abb. 4.18 kann man entnehmen, dass der Flächenvektor A
~
das Magnetfeld B ebenfalls den Winkel ϑ einschließen. Damit kann man das
Drehmoment in Gl. (4.32) vektoriell schreiben in der Form
~ =m
~ .
M
~ ×B
(4.34)
Wir haben Gl. (4.34) hergeleitet für rechteckförmige Leiterschleifen. Man kann
aber zeigen, dass das Resultat auch gültig bleibt für beliebig geformte ebene
Leiterschleifen (Übungsaufgabe). Besteht die Leiterschleife nicht nur aus einer Windung sondern N Windungen, so tragen natürlich alle N Windungen
gleichermassen zum Drehmoment bei. Das magnetische Dipolmoment einer
Leiterschleife mit N Windungen ist damit allgemein definiert durch:
~ .
m
~ =NIA
(4.35)
Behält man die Stromrichtung in der Leiterschleife bei, so dreht sich die
Leiterschleife solange, bis sich das magnetische Dipolmoment m
~ parallel zu dem
~
Magnetfeld B einstellt. Will man aber wie bei einem Elektromotor die Drehung
aufrecht erhalten, so muss die Richtung des Stromes nach jeder Drehung um
~ gerichtet ist)
1800 im richtigen Moment (wenn m
~ parallel oder antiparallel zu B
umgepolt werden. Dies kann man, wie in Abb. 4.17 dargestellt, mit Hilfe eines
sogenannten Kommutators bestehend aus zwei halbkreisförmigen Kontakten
und zwei Bürsten erreichen.
4.6
Der HALL-Effekt
In diesem Abschnitt untersuchen wir für eine konkrete Leiteranordnung, wie
sich ein Magnetfeld auf die Verteilung der Ladungsträger in einem stromdurchflossenen Leiter auswirkt. Wir betrachten einen dünnen Leiter mit rechteckförmigem Querschnitt, durch den in horizontale Richtung von links nach
84
4 Das magnetische Feld
Abbildung 4.19: Der HALL-Effekt.
rechts ein Strom I fließe, siehe Abb. 4.19. Der Leiter habe die Breite b und
die Dicke d. Wir nehmen an, dass der Strom durch positive Ladungsträger der
Dichte n und der Ladung q zustande kommt, die sich mit der Driftgeschindigkeit ~v nach rechts durch den Leiter bewegen. Der Leiter befinde sich in
~ dass senkrecht in die Zeichenebene hineineinem homogenen Magnetfeld B,
zeigt. Die Ladungsträger erfahren dann eine nach oben gerichtete LORENTZKraft FL = q v B, die sie nach oben ablenkt. Auf diese Weise entsteht oben ein
Überschuss und unten ein Mangel an positiven Ladungsträgern, wodurch senk~ aufgebaut wird. Dieses Feld zeigt
recht zum Strom I ein elektrisches Feld E
in Abb. 4.19 von oben nach unten und übt auf die Ladungsträger q die nach
unten gerichtete COULOMB-Kraft FC = q E aus. Die Aufladung des Leiters
nimmt nun solange zu, bis sich zwischen der LORENTZ-Kraft FL = q v B und
der COULOMB-Kraft FC = q E ein Gleichgewicht einstellt,
qE = qvB .
Das elektrische Feld erreicht also den Wert
E = vB .
(4.36)
Für den Strom I gilt nach Gl. (3.3) I = q n v A, wobei v die Driftgeschwindigkeit der Ladunsträger ist, n die Ladungsträgerdichte und A die Querschnittsfläche des Leiters. Damit ergibt sich für v
v=
I
.
qnA
85
4.7 Bahnen freier Ladungen im Magnetfeld
Setzt man dies in Gl. (4.36) ein, und berücksichtigt den rechteckförmigen Querschnitt des Leiters mit der Fläche A = b d, so folgt für das elektrische Feld
E=
IB
IB
=
.
qnA
qnbd
(4.37)
Die zugehörige Spannungsdifferenz zwischen der Oberkante und der Unterkante des Leiters wird als HALL-Spannung UH bezeichnet. Sie ergibt sich mit
Gl. (4.37) zu
IB
IB
UH = E b =
= RH
.
(4.38)
qnd
d
Hierbei ist
RH =
1
qn
die sogenannte HALL-Konstante, die für jedes Leitermaterial einen besimmten
Wert hat. Aus Gl. (4.38) lassen sich direkt einige Anwendungen des HALLEffektes ablesen. Wegen der Proportionalität der HALL-Spannung UH zum
Magnetfeld B kann durch Messen der HALL-Spannung leicht die Stärke eines Magnetfeldes gemessen werden. Dies geschieht mittels sogenannter HALLSonden. Man kann weiterhin durch Messen der HALL-Konstanten RH die Ladungsträgerdichte n des Leitermaterials ermitteln. Schließlich kann man auch
ermitteln, ob der Strom durch positive oder negative Ladungsträger zustande
kommt. Läßt man in Abb. 4.19 negative Ladungsträger von rechts nach links
wandern, so bleibt die technische Stromrichtung dieselbe wie in Abb. 4.19. Da
die LORENTZ-Kraft auch in diesem Fall nach oben zeigt, sammeln sich nun
~
negative Ladungsträger an der Oberkante des Leiters. Damit zeigt das E-Feld
aber von unten nach oben und das Vorzeichen der HALL-Spannung kehrt sich
um.
4.7
Bahnen freier Ladungen im Magnetfeld
~ auf ein
Wir hatten in Abschnitt 4.1 gesehen, dass von einem Magnetfeld B
geladenes Teilchen, das sich mit der Geschwindigkeit ~v in dem Magnetfeld be~ ausgeübt wird. Ein wichtiges Merkwegt, die LORENTZ-Kraft F~ = q (~v × B)
mal der LORENTZ-Kraft ist, dass sie stets senkrecht zur Bewegungsrichtung
wirkt. Daher wird zwar die Richtung, nicht aber der Betrag der Geschwindigkeit des Teilchens geändert. Das Magnetfeld leistet somit keine Arbeit an
dem Teilchen und hat somit auch keinen Einfluss auf seine kinetische Energie.
Bewegt sich ein geladenes Teilchen genau senkrecht zu einem homogenen Magnetfeld (siehe Abb. 4.20), so führt die Richtung der Kraftwirkung dazu, dass
86
4 Das magnetische Feld
Abbildung 4.20: Eine geladenes Teilchen bewegt sich auf einer Kreisbahn senkrecht zu einem homogenen Magnetfeld.
das geladene Teilchen im Magnetfeld eine Kreisbahn beschreibt. Für die notwendige Zentripetalbeschleunigung kommt gerade die LORENTZ-Kraft auf.
Oder, wenn wir den Standpunkt des mitrotierenden Beobachters einnehmen,
so ist die Kreisbahn dadurch bestimmt, dass der Betrag der Zentrifugalkraft
mv 2 /r und der Betrag der LORENTZ-Kraft qvB dort gleich sein müssen, also
qvB = m
oder
r=
v2
r
mv
.
qB
(4.39)
Das heisst, der Radius r der Kreisbahn nimmt proportional mit der Geschwindigkeit v zu. Aus Gl. (4.39) können wir für die Winkelgeschwindigkeit oder
Kreisfrequenz ω = v/r ablesen
ω=
v
qB
=
.
r
m
(4.40)
~ hängt die Winkelgeschwindigkeit oder
In einem homogenen Magnetfeld B
Kreisfrequenz ω für eine bestimmte Teilchensorte nur von der Stärke des Magnetfeldes ab.
Obige Frequenz wird entscheidend ausgenutzt bei einem Zyklotron, weshalb
sie auch als Zyklotronfrequenz ωc = q B/m bezeichnet wird. Ein Zyklotron
(siehe Abb. 4.21) ist ein Teilchenbeschleuniger, bei dem die geladenen Teilchen durch eine Wechselspannung, angelegt zwischen zwei hohlen, D-förmigen
Leitern, auf Touren“ gebracht werden. Die Leiter haben jeder die Form einer
”
4.7 Bahnen freier Ladungen im Magnetfeld
87
senkrecht in der Mitte durchgeschnittenen Dose. Das elektrische Feld zwischen
den D-förmige Elektroden wirkt auf die im Zentrum von der Quelle S emittierten, geladenen Teilchen im Takt ihrer Zyklotronfrequenz. Diese werden
dadurch bei jedem Durchgang durch das elektrische Feld beschleunigt, wobei
sich der Bahnradius entsprechend immer weiter vergrößert. Die Teilchen werden nur in dem Zwischenraum zwischen den Dosen beschleunigt, denn innerhalb jeder Dose verschwindet das elektrische Feld. Die Geschwindigkeit und
der Radius nehmen bei jedem Umlauf zu, die Kreisfrequenz ωc aber bleibt
gleich. Der entscheidende Punkt dafür, dass sich die Geschwindigkeit erhöht,
ist natürlich, dass die Wechselspannung mit der Kreisfrequenz ωc in Phase mit
den umlaufenden Teilchen angewandt wird. Die Teilchen laufen dann auf einer
spiralförmigen Bahn nach außen, bis sie durch eine geeignete Ablenkelektrode
aus dem Zyklotron herausgeführt werden.
Abbildung 4.21: Aufbau eines Zyklotrons.
88
4 Das magnetische Feld
Kapitel 5
Induktion
5.1
Das FARADAYsche Induktionsgesetz
Um 1830 führte FARADAY zahlreiche Experimente durch, mit dem Ziel mit
Hilfe von Magnetfeldern elektrische Ströme zu erzeugen. Er fand dabei folgendes Gesetz, das als FARADAYsches Induktionsgesetz bezeichnet wird:
Ein zeitlich sich ändernder magnetischer Fluss durch eine Leiterschleife ruft in dieser eine elektrische Spannung hervor. Es gilt:
Uind = −
dΦ
.
dt
(5.1)
Hierbei ist Uind die in der Leiterschleife induzierte Spannung und Φ der magnetische Fluss durch die Leiterschleife, also
Φ=
Z
~ dA
~ .
B
(5.2)
A
A bezeichnet dabei die von der Leiterschleife eingeschlossene Fläche. Die induzierte Spannung hat die gleiche Wirkung wie die Leerlaufspannung einer Batterie. Sie ruft in der Leiterschleife, wenn diese geschlossen wird, einen induzierten Strom hervor. Wie die Leerlaufspannung einer Batterie wird die induzierte
Spannung Uind manchmal mit dem veralteten Bergriff elektromotorische Kraft
(EMK) bezeichnet.
Das FARADAYsche Induktionsgesetz kann mit der Versuchsanordnung in
Abb. 5.1 veranschaulicht werden. Sie besteht aus einer einfachen Drahtschleife,
die sich im Magnetfeld eines Stabmagneten befindet, und die an ein Spannungsmessgerät angeschlossen ist. Wenn sich der Fluss des Magnetfeldes durch die
89
90
5 Induktion
Abbildung 5.1: Versuchsanordnung zur Demonstration des FARADAYschen
Induktionsgesetzes.
Drahtschleife nicht ändert, tritt an den Enden der Drahtschleife keine Spannung auf. Sobald sich aber durch Annäherung oder Entfernen des Stabmagneten der magnetische Fluss in der Drahtschleife ändert, tritt eine induzierte
Spannung gemäß Gl. (5.1) auf. Durch Drehen der Drahtschleife im Magnetfeld
des Stabmagneten kann der magnetische Fluss durch die Drahtschleife ebenfalls geändert werden. Auch in diesem Fall zeigt sich eine induzierte Spannung
gemäß Gl. (5.1).
~
Die induzierte Spannung Uind ist verbunden mit einem elektrischen Feld E,
das sich entlang der Leiterschleife ausbreitet. Es gilt
Uind =
I
~ d~r ,
E
(5.3)
C
wobei das Linienintegral entlang der Leiterschleife ausgeführt werden muss.
Dieses elektrische Feld bewirkt gerade die Bewegung der Ladungsträger bei
dem elektrischen Strom, der eintritt, sobald die Leiterschleife z.B. über einen
Widerstand geschlossen wird. Mit den Gln. (5.2) und (5.3) kann man das
FARADAYsche Induktionsgesetz (5.1) auch schreiben in der Form
I
C
d Z ~ ~
~
E d~r = −
B dA .
dt
(5.4)
A
Hierbei ist darauf zu achten, dass die Orientierung der Fläche A und die Orientierung der sie berandenden Kurve C durch einen Rechtsschraubensinn mitein-
91
5.2 Die LENZsche Regel
ander verbunden sind. Das FARADAYsche Induktionsgesetz in der Form (5.4)
ist insofern allgemeiner als Gl. (5.1), als es nicht an das Vorhandensein einer
Leiterschleife gebunden ist. Gemäß Gl. (5.4) ruft ein zeitlich sich änderndes
Magnetfeld stets ein elektrisches Feld hervor. Dies ist für die Ausbreitung von
elektromagnetischen Wellen von fundamentaler Bedeutung, wie wir in Kap. 6.4
noch sehen werden. Mit einer Leiterschleife kann das Vorhandensein des elektrischen Feldes durch die damit verbundene induzierte Spannung oder den
damit verbundenen elektrischen Strom nachgewiesen werden.
5.2
Die LENZsche Regel
Nach dem OHMschen Gesetz führt die induzierte Spannung Uind zu einem
Strom
1 dΦ
1 d Z ~ ~
Uind
=−
=−
I=
B dA
(5.5)
R
R dt
R dt
A
in der Leiterschleife, wenn R der gesamte ohmsche Widerstand der Leiterschleife ist. Die Richtung der Induktionsspannung und des induzierten Stroms ist
zwar durch Gl. (5.5) gegeben, die Auswertung ist aber oft unhandlich, weil man
zunächst die Fläche A und die sie berandende Kurve C so orientieren muss,
dass sie durch einen Rechtsschraubensinn miteinander verbunden sind, und
dann muss noch das Minuszeichen berücksichtigt werden. Hier ist die LENZsche Regel hilfreich, mit der man sich die Richtung der Induktionsspannung
und des induzierten Stroms einfacher klar machen kann. Sie lautet:
Die Induktionsspannung und der Induktionsstrom, sind immer so
gerichtet, dass sie der Flussänderung, die sie hervorruft, entgegenwirken.
Wir wollen die Anwendung der LENZschen Regel anhand der in Abb. 5.2 dargestellten Anordnung illustrieren. Sie besteht aus einem Stabmagneten und
einer ringförmigen Drahtschleife, welche den Widerstand R besitzt. Das Magnetfeld des Stabmagneten zeigt nach links aus dem Nordpol des Magneten
heraus. Bewegt sich der Magnet auf die Drahtschleife zu (siehe Abb. 5.2a), so
erhöht sich der magnetische Fluss durch die Drahtschleife, weil das Magnetfeld
in der Nähe des Nordpols stärker ist als in größerer Entfernung von ihm. Der
Strom, der in der Drahtschleife induziert wird, erzeugt selbst wieder ein Magnetfeld. Er fließt nun in die Richtung, so dass das von ihm erzeugte Magnetfeld
dem des Stabmagneten entgegengerichtet ist, siehe Abb. 5.2a. Der Strom ist
also so gerichtet, dass er der Zunahme des magnetischen Flusses entgegenwirkt.
Wird umgekehrt der Magnet von der Drahtschleife entfernt (siehe Abb. 5.2b),
92
5 Induktion
Abbildung 5.2: Zur Anwendung der LENZschen Regel. Der Stabmagnet wird
auf die Leiterschleife zubewegt (a). Der Stabmagnet wird von der Leiterschleife
entfernt (b).
so nimmt der magnetische Fluss durch die Drahtschleife ab. Der Strom, der
jetzt in der Drahtschleife induziert wird, fließt in die entgegengesetze Richtung
wie bei der Situation (a). Er ist so gerichtet, dass das von ihm erzeugte Magnetfeld die gleiche Richtung hat wie das des Stabmagneten, siehe Abb. 5.2b.
Der Strom ist also so gerichtet, dass er die Abnahme des magnetischen Flusses
zu verhindern versucht. In beiden Fällen (a) und (b) ist der induzierte Strom
also so gerichtet, dass er seiner Ursache, nämlich der Änderung des magnetischen Flusses entgegenwirkt, was gerade die Aussage der LENZschen Regel
ist.
Wir können das ganze auch noch auf folgende Weise verstehen. Nach
Gl. (4.33) kann jedem Strom ein magnetisches Moment m
~ zugeordnet werden. Dieses steht senkrecht auf der Leiterschleife und ist mit der Richtung
des Stroms I in einem Rechtsschraubensinn verbunden. Es zeigt in Abb. 5.2a
demzufolge nach rechts. Die Drahtschleife wirkt damit selber wie ein kleiner
Magnet mit Nordpol rechts und Südpol links. Da sich gleichnamige Pole abstoßen, wirkt eine Kraft der Annäherung des Stabmagneten entgegen. Umgekehrt
zeigt in Abb. 5.2b das magnetische Moment der Drahtschleife nach links. Die
Drahtschleife wirkt damit wie ein kleiner Magnet mit Nordpol links und Südpol
rechts. Da sich ungleichnamige Pole anziehen, wirkt hier eine Kraft dem Entfernen des Stabmagneten von der Drahtschleife entgegen. In beiden Fällen (a)
und (b) ist das magnetische Moment des induzierten Stroms so gerichtet, dass
es seine Ursache, nämliche die Bewegung des Stabmagneten abzubremsen versucht.
Die LENZsche Regel folgt direkt aus dem Energieerhaltungssatz. Würde
in der in Abb. 5.2a dargestellten Situation der Strom in die Gegenrichtung
fließen, so wäre auch das magnetische Moment entgegengesetzt gerichtet. Es
würde dann auf den Stabmagneten eine anziehende Kraft ausüben. Ein leich-
93
5.3 Beispiele zum Induktionsgesetz
tes Anstoßen des Stabmagneten in Richtung der Drahtschleife hätte dann zur
Folge, dass der Magnet zur Drahtschleife hin beschleunigt würde. Dies würde
den induzierten Strom weiter erhöhen, was eine noch stärkere Beschleunigung
zur Folge hätte und so fort. Der Magnet würde sich letztlich immer schneller
auf die Drahtschleife zubewegen, und auf Grund des induzierten Stroms würde
in der Drahtschleife immer mehr JOULEsche Wärme erzeugt, obwohl dem System keinerlei Energie zugeführt wird. Dies wäre eine offensichtliche Verletzung
des Energiesatzes. Tatsächlich ist es so, dass die JOULEsche Wärme, die in
der Drahtschleife mit dem Widerstand R erzeugt wird, gerade der kinetischen
Energie des Stabmagneten entzogen wird.
5.3
Beispiele zum Induktionsgesetz
In diesem Abschnitt wollen wir einige Beispiele zum Induktionsgesetz untersuchen. Wir betrachten als erstes die in Abb. 5.3 dargestellte Leiterschleife. Sie
besteht aus zwei parallelen Metallschienen, die links durch einen Widerstand R
verbunden sind. Rechts wird die Leiterschleife geschlossen durch einen beweglichen Metallstab. Dieser wird mit der konstanten Geschwindigkeit v gleitend
über die Schienen nach rechts bewegt. Der Abstand der parallelen Schienen
voneinander sei l, und der Abstand des beweglichen Metallstabes vom linken
Schienenende sei x. Die gesamte Leiterschleife befindet sich in einem homoge~ welches senkrecht in die Zeicheneben hineinzeigt. Wird der
nen Magnetfeld B,
bewegliche Metallstab mit der Geschwindigkeit v nach rechts bewegt, so gilt
x = v t. Damit nimmt die Fläche A = l x der Leiterschleife proportional zur
Zeit t zu und ebenso der magnetische Fluss Φ = B l x durch die Leiterschleife.
Dies liefert die induzierte Spannung
dΦ
d
= − B lx = −B lv ,
(5.6)
dt
dt
wobei v = dx/dt die Geschwindigkeit des bewegten Metallstabes ist. Wir erhalten auf diese Weise einen Gleichspannungsgenerator. Befindet sich in der
Leiterschleife, wie in Abb. 5.3 dargestellt, ein Verbraucher mit dem Widerstand R, so fließt auf Grund der induzierten Spannung ein induzierter Strom
I der Stärke
Blv
|Uind |
=
(5.7)
I=
R
R
in die in Abb. 5.3 eingezeichnete Richtung. Durch diesen Strom wird im Widerstand R die elektrische Leistung
Uind = −
Pel = R I 2 =
B 2 l2 v 2
R
(5.8)
94
5 Induktion
Abbildung 5.3: Eine Leiterschleife mit einem beweglichen Metallstab rechts.
~
Die gesamte Leiterschleife befindet sich in einem homogenen Magnetfeld B,
das senkrecht in die Zeicheneben hineinzeigt.
verbraucht. Es stellt sich die Frage, auf welche Weise diese Leistung dem System zugeführt wird. Nach Gl. (4.4) erfährt der stromdurchflossene Metallstab
eine LORENTZ-Kraft vom Betrag F = I l B. Sie ist in Abb. 5.3 nach links gerichtet. Um den Metallstab mit der konstanten Geschwindigkeit v nach rechts
zu verschieben, müssen wir eine entsprechende, gleich große Gegenkraft nach
rechts aufbringen. Mit Gl. (5.7) berechnet sich die für die Verschiebung des
Stabes erforderliche mechanische Leistung zu
Pmech = F v = I l B v =
B 2 l2 v 2
.
R
(5.9)
Die Gleichheit von Pmech und Pel bedeutet nichts anderes als die Energieerhaltung. Die mechanische Leistung, die für das Verschieben des Metallstabes
aufgebracht werden muss, wird durch den induzierten Strom in Form von elektrischer Leistung an dem Widerstand R wieder abgeführt.
Mittels einer rotierenden Leiterschleife in einem Magnetfeld läßt sich eine
Wechselspannung erzeugen, siehe Abb. 5.4. Die Leiterschleife befinde sich in ei~ Der magnetische Fluss durch die Leiterschleife
nem homogenen Magnetfeld B.
mit der Fläche A = a b beträgt
Φ = B A cos ϑ ,
~ einwobei ϑ der Winkel ist, den die Flächennormale ~n und das Magnetfeld B
schließen. Rotiert die Leiterschleife mit der konstanten Winkelgeschwindigkeit
5.3 Beispiele zum Induktionsgesetz
95
Abbildung 5.4: Das Prinzip des Wechselstromgenerators. Die Leiterschleife
wird in einem homogenen Magnetfeld gedreht.
ω im Gegenuhrzeigersinn, so gilt ϑ = ω t, und man erhält an den Enden der
Leiterschleife die induzierte Spannung
Uind = −
dΦ
d
= − B A cos(ω t) = B A ω sin(ω t) .
dt
dt
Ersetzt man die einfache Leiterschleife durch eine Leiterschleife (Spule) mit N
Windungen so ergibt sich die induzierte Spannung zu
Uind = N B A ω sin(ω t) .
(5.10)
Verbindet man die Enden der Leiterschleife durch einen Verbraucher mit dem
Widerstand R, so fließt durch die Leiterschleife der induzierte Strom
I=
Uind
N B A ω sin(ω t)
=
.
R
R
(5.11)
Durch diesen Strom wird am Verbraucher mit dem Widerstand R die elektrische Leistung Pel = R I 2 abgeführt. Diese berechnet sich mit Gl. (5.11) zu
Pel = R I 2 =
N 2 B 2 A2 ω 2 sin2 (ω t)
.
R
(5.12)
96
5 Induktion
Auch hier stellt sich die Frage, auf welche Weise diese Leistung dem System
zugeführt wird. Durch den induzierten Strom I erfährt die Spule in dem Ma~ gemäß Gl. (4.34) das Drehmoment
gnetfeld B
Dabei ist
~ =m
~ .
M
~ ×B
(5.13)
~
m
~ =NIA
(5.14)
das magnetische Moment einer Leiterschleife mit N Windungen, siehe
~ = A ~n bezeichnet den zugehörigen Flächenvektor. Der Betrag
Gl. (4.35). A
~ berechnet sich mit den Gl. (5.13) und (5.14) zu
des Drehmoments M
M = N I A B sin ϑ = N I A B sin(ω t) ,
(5.15)
da ϑ = ω t der Winkel ist, den die Flächennormale ~n und das Magnetfeld
~ einschließen. Zur Aufrechterhaltung der Drehung der Leiterschleife muss
B
ein entsprechendes, vom Betrag gleich großes Drehmonent aufgebracht werden. Dazu ist die mechanische Leistung Pmech = M ω erforderlich. Mit den
Gln. (5.15) und (5.11) berechnet sich diese zu
Pmech = M ω = N I A B ω sin(ω t) =
N 2 B 2 A2 ω 2 sin2 (ω t)
.
R
(5.16)
Auch hier zeigt sich die Energieerhaltung Pmech = Pel . Um die Leiterschleife
~ zu drehen, muss dem System die mechanische Leistung
in dem Magnetfeld B
Pmech zugeführt werden. Diese wird durch den induzierten Strom als elektrischer Leistung Pel an dem Widerstand R wieder abgeführt. Diese Anwendung
der Induktion ist von überragender Bedeutung in der Technik. Nahezu die gesamte, weltweit erzeugte Energie wird mittels Generatoren aus mechanischer
Energie gewonnen.
In den bisher besprochenen Fällen wurden Induktionsströme nur in Drähten
und Leitungen z.B. einer Spule erzeugt. Aber auch in kompakten Metallen werden Kreisströme bei Änderung des magnetischen Flusses erzeugt. Diese Kreisströme nennt man Wirbelströme. In Abb. 5.5 ist eine Anordnung dargestellt,
mit der sich das Auftreten von Wirbelströmen zeigen lässt. Am Ende eines
Pendels ist eine Aluminiumscheibe befestigt. Versucht man nun, diese Scheibe durch die Pole eines starken Hufeisenmagneten durchschwingen zu lassen,
so wird man feststellen, dass die Scheibe deutlich abgebremst wird, obwohl
keine Berührung zwischen der Scheibe und dem Magneten stattfindet. Der
Grund ist folgender. Wenn die Scheibe in das Magnetfeld des Hufeisenmagneten eindringt, ändert sich der magnetische Fluss durch jede geschlossene
97
5.4 Gegeninduktion
Kurve in dem Metall. Somit wird längs jeder Kurve eine Spannung induziert
und es fließt ein geschlossener Strom. Die Richtung dieser Ströme wird durch
die LENZsche Regel festgelegt. Auf diese Ströme wirkt die LORENTZkraft,
welche die Metallscheibe sowohl beim Hineinbewegen in den Magneten, als
auch beim Herausbewegen aus dem Magneten abbremst. Dieses Prinzip der
Wirbelstrombremse findet in der Technik vielfältige Anwendung. Aber auch
bei der Magnet-Schwebebahn werden entscheidend Wirbelströme ausgenutzt.
Abbildung 5.5: Anordnung zur Demonstration des Auftretens von Wirbelströmen.
5.4
Gegeninduktion
In diesem Abschnitt wollen wir uns noch etwas genauer mit dem Phänomen der
Induktion beschäftigen und zwar mit der Gegeninduktion. Wir betrachten dazu
die Anordnung in Abb. 5.6 bestehend aus den beiden Leiterschleifen C1 und
C2 . Fließt durch die Leiterschleife C1 ein Strom I1 , so entsteht ein Magnetfeld
~ 1 und in der Leiterschleife C2 wird der magnetische Fluss Φ21 erzeugt mit
B
Φ21 =
Z
A2
~ 1 dA
~2 ,
B
98
5 Induktion
Abbildung 5.6: Zur Gegeninduktion. Fließt durch die Leiterschleife C1 ein
~ 1 und in der Leiterschleife C2 wird
Strom I1 , so entsteht ein Magnetfeld B
der magnetische Fluss Φ21 erzeugt.
wobei A2 die von der Leiterschleife C2 berandete Fläche ist. Aus dem BIOT~ 1 proportional zu dem
SAVARTschen Gesetz ergibt sich, dass das Magnetfeld B
Strom I1 ist. Damit ist aber auch der Fluss Φ21 proportional zu I1 , also
Φ21 = M21 I1 .
(5.17)
Ändert sich der Strom I1 mit der Zeit, so wird gemäß dem FARADAYschen
Induktionsgesetz in der Leiterschleife C2 eine Spannung U21 induziert mit
dΦ21
dI1
= − M21
.
(5.18)
dt
dt
Die Proportionalitätskonstante M21 in Gl. (5.17) wird als Gegeninduktivität
bezeichnet. Sie wird in der Einheit Henry (H) gemessen. Aus Gl. (5.18) ergibt
sich für diese Einheit
Vs
H=
.
A
Fließt umgekehrt durch die Leiterschleife C2 ein Strom I2 , so entsteht ein
~ 2 und in der Leiterschleife C1 wird der magnetische Fluss Φ12
Magnetfeld B
erzeugt mit
Z
~ 2 dA
~1 ,
Φ12 = B
U21 = −
A1
wobei A1 die von der Leiterschleife C1 berandete Fläche ist. Aus dem BIOT~ 2 proportional zu dem
SAVARTschen Gesetz ergibt sich, dass das Magnetfeld B
Strom I2 ist. Damit ist aber auch der Fluss Φ12 proportional zu I2 , also
Φ12 = M12 I2 .
(5.19)
99
5.4 Gegeninduktion
Ändert sich der Strom I2 mit der Zeit, so wird gemäß dem FARADAYschen
Induktionsgesetz in der Leiterschleife C1 eine Spannung U12 induziert mit
U12 = −
dI2
dΦ12
= − M12
.
dt
dt
(5.20)
Die Gegeninduktivitäten M21 und M12 hängen von der geometrischen Form der
beiden Leiterschleifen C1 und C2 und der geometrischen Anordnung der beiden
Leiterschleifen zueinander ab. Ihre Berechnung kann im Einzelfall durchaus
kompliziert sein. Es lässt sich aber der Reziprozitätssatz beweisen, der aussagt,
dass ganz allgemein gilt:
M12 = M21 .
(5.21)
Das bedeutet, für konkrete Anordnungen muss nur eine der Gegeninduktivitäten berechnet werden, wobei man dann geschickterweise die einfacher zu
ermittelnde berechnet.
Als konkretes Beispiel berechnen wir die Gegeninduktivität zweier langer
Spulen, die konzentrisch ineinander liegen, siehe Abb. 5.7. Beide Spulen haben
die Länge l, die äußere habe die Querschnittsfläche A1 die innere die Querschnittsfläche A2 . Die äußere habe N1 Windungen und die innere N2 . Wir
setzten weiter voraus, dass die Länge l der Spulen viel größer ist, als ihre Querabmessungen. Das bedeutet, fließt durch eine der Spulen ein Strom, so wird im
Innern der jeweiligen Spule ein homogenes Magnetfeld erzeugt, während das
Magnetfeld im Außenraum der Spule veschwindet. Fließt z.B. durch die äußere
Abbildung 5.7: Zur Berechnung der Gegeninduktivität zweier langer Spulen,
die konzentrisch ineinander liegen.
100
5 Induktion
~1
Spule 1 der Strom I1 , so wird in ihrem Innern ein homogenes Magnetfeld B
erzeugt, für das gemäß Gl. (4.29) gilt:
B 1 = µ0
N1
I 1 = µ 0 n1 I 1 ,
l
wobei n1 = N1 /l die Wicklungsdichte der Spule 1 ist. In den N2 Windungen
der inneren Spule 2 bewirkt dieses Magnetfeld den Fluss
Φ21 = N2 B1 A2 = µ0
N1 N2
A2 I1 .
l
Durch Vergleich mit der Definitionsgleichung der Gegeninduktivität, Gl. (5.17),
ergibt sich für die Gegeninduktivität M21 dieser Anordnung
M21 = µ0
N1 N2
A2 = µ0 n1 n2 A2 l ,
l
(5.22)
wobei n2 = N2 /l die Wicklungsdichte der Spule 2 ist.
Fließt umgekehrt durch die innere Spule 2 der Strom I2 so wird in ihrem
~ 2 erzeugt, das gemäß Gl. (4.29) gegeben
Innern ein homogenes Magnetfeld B
ist durch
N2
I 2 = µ 0 n2 I 2 .
B 2 = µ0
l
Im Außenraum der Spule verschwindet das Magnetfeld. In den N1 Windungen
der äußeren Spule 1 bewirkt dieses Magnetfeld den Fluss
Φ12 = N1 B2 A2 = µ0
N1 N2
A2 I2 .
l
Durch Vergleich mit der Definitionsgleichung der Gegeninduktivität, Gl. (5.19),
ergibt sich für die Gegeninduktivität M12 dieser Anordnung
M12 = µ0
N1 N2
A2 = µ0 n1 n2 A2 l = M21 ,
l
(5.23)
Für die einfache Anordnung zweier langer Spulen, die konzentrisch ineinander
liegen, konnten wir damit die Gültigkeit des Reziprozitätssatzes sogar nachweisen.
5.5
Selbstinduktion
Aber auch wenn wir nur eine Leiterschleife haben, tritt bei zeitlich veränderlichen Strömen der Effekt der Induktion auf. Man spricht dann von Selbstinduktion. Wir betrachten dazu die Anordnung in Abb. 5.8 bestehend aus nur
101
5.5 Selbstinduktion
Abbildung 5.8: Zur Selbstinduktion. Fließt durch eine Leiterschleife C ein
~ und in der Leiterschleife wird der maStrom I, so entsteht ein Magnetfeld B
gnetische Fluss Φ erzeugt.
einer Leiterschleife C. Fließt durch die Leiterschleife C ein Strom I, so ent~ und in der Leiterschleife wird ein
steht um die Leiterschleife ein Magnetfeld B,
magnetische Fluss Φ erzeugt mit
Φ=
Z
~ dA
~ ,
B
A
wobei A die von der Leiterschleife berandete Fläche ist. Aus dem BIOT~ proportional zu dem
SAVARTschen Gesetz ergibt sich, dass das Magnetfeld B
Strom I ist. Damit ist aber auch der Fluss Φ proportional zu I, also
Φ = LI .
(5.24)
Ändert sich der Strom I mit der Zeit, so wird gemäß dem FARADAYschen
Induktionsgesetz in der Leiterschleife C eine Spannung Uind induziert mit
Uind = −
dΦ
dI
= −L
.
dt
dt
(5.25)
Die Proportionalitätskonstante L in Gl. (5.24) bzw. Gl. (5.25) wird als Selstinduktivität oder meist kurz Induktivität der Leiterschleife bezeichnet. Sie wird
wie die Gegeninduktivität in der Einheit Henry (H) gemessen. Das negative
Vorzeichen in Gl. (5.25) drückt wie gehabt aus, dass die induzierte Spannung
Uind der Stromänderung entgegenwirkt (LENZsche Regel).
102
5 Induktion
Als konkretes Beispiel berechnen wir die Induktivität einer langen Spule.
Die Spule habe die Länge l und die Querschnittsfläche A. Sie habe außerdem
N Windungen. Wir setzten weiter voraus, dass die Länge l der Spule viel größer
ist als ihre Querabmessungen. Das bedeutet, fließt durch die Spule ein Strom,
so wird im Innern der Spule ein homogenes Magnetfeld erzeugt, während das
~ im Inneren der
Magnetfeld im Außenraum veschwindet. Für das Magnetfeld B
Spule gilt gemäß Gl. (4.29):
B = µ0
N
I = µ0 n I ,
l
wobei n = N/l die Wicklungsdichte der Spule ist, und I der Strom, der durch
die Spule fließt. In den N Windungen der Spule bewirkt dieses Magnetfeld den
Fluss
N
N2
Φ = N B A = N µ0 I A = µ0
AI .
l
l
Durch Vergleich mit der Definitionsgleichung der Induktivität, Gl. (5.24), ergibt sich für die Induktivität einer langen Spule
L = µ0
N2
A = µ 0 n2 A l .
l
(5.26)
Ein weiteres technisch wichtiges Beispiel ist das schon in Abschitt 4.4 behandelte Koaxialkabel, dessen Induktivität wir jetzt berechnen wollen. Ein
Koaxialkabel besteht aus zwei koaxialen Metallzylindern, in denen antiparallel
der Strom I fließt, siehe Abb. 5.9. Der innere Zylinder habe den Radius a, der
äußere den Radius b. Ist die Länge l des Koaxialkabels groß verglichen mit
den Querabmessungen, so können wir Randeffekte vernachlässigen, und das
Magnetfeld im Innern des Kabels ist gemäß Gl. (4.28) gegeben durch
B=
µ0 I
.
2π r
(5.27)
Die Magnetfeldlinien laufen dabei kreisförmig um den Innenleiter. Der magnetische Fluss Φ durch die schraffierte Fläche A zwischen Innen- und Außenleiter
in Abb. 5.9 beträgt
Φ =
Z
~ dA
~ =
B
Z l Zb
0 a
A
b
µ0 I
dr dx
2π r
!
Z
µ0
1
µ0
b
=
Il
dr =
l ln
I .
2π
r
2π
a
a
103
5.5 Selbstinduktion
Abbildung 5.9: Zur Berechnung der Induktivität eines Koaxialkabels.
Durch Vergleich mit der Definitionsgleichung der Induktivität, Gl. (5.24), ergibt sich für die Induktivität eines Koaxialkabels der Länge l
b
µ0
l ln
L=
2π
a
!
.
(5.28)
Betrachtet man nur ein Stück der Länge x des Koaxialkabels, so hat dieses die
Induktivität
!
µ0
b
L(x) =
.
(5.29)
x ln
2π
a
Diese Induktivität führt dazu, dass sich bei einer zeitlichen Änderung des
Stroms (auch ohne jeden ohmschen Widerstand) die Spannung zwischen Innenund Außenleiter des Koaxialkabels mit der Position x entlang des Koaxialkabels so ändert, dass gilt
U (x) − U (0) = − L(x)
dI
.
dt
Zum Abschluss wollen wir noch die Reihen- und Parallelschaltung von Induktivitäten betrachten. Bei einer Reihenschaltung (Abb. 5.10a) addieren sich
die induzierten Spannungen einfach. Das heißt, es gilt
Uind = Uind,1 + Uind,2 = −L1
dI
dI
dI
− L2
= −(L1 + L2 )
.
dt
dt
dt
Vergleicht man dies mit der allgemeinen Definitionsgleichung für die Induktivität, Uind = −L dI/dt, so sehen wir: Die Reihenschaltungschaltung zweier
104
5 Induktion
Induktivitätentäten L1 und L2 besitzt eine Gesamtinduktivität L mit
L = L1 + L2 .
Bei der Parallelschaltung (Abb. 5.10b) gilt Uind,1 = Uind,2 =: Uind und nach
dem zweiten KIRCHHOFFschen Gesetz I = I1 + I2 . Daraus folgt:
dI1 dI2
Uind Uind
dI
=
+
=−
−
=−
dt
dt
dt
L1
L2
1
1
+
L1 L2
Uind .
Vergleicht man dies mit der allgemeinen Definitionsgleichung für die Induktivität, Uind = −L dI/dt, so sehen wir: Die Parallelschaltung zweier Induktivitäten L1 und L2 besitzt eine Gesamtinduktivität L mit
1
1
1
=
+
.
L
L1 L2
Abbildung 5.10: Reihenschaltung (a) und Parallelschaltung (b) von Induktivitäten.
5.6
Der RL-Kreis
Das Auftreten einer selbstinduzierten Spannung gemäß Gl. (5.25) läßt sich am
einfachsten erkennen, wenn man einen Strom durch eine Spule mit der Induktivität L ein- oder ausschalten will, siehe Abb. (5.11). Denn beim Ein- oder
Ausschalten ist die Stromänderung dI/dt besonders groß und damit auch die
induzierte Spannung Uind = −L dI/dt. Wir betrachten zunächst den Einschaltvorgang, also die Situation, wenn der Schalter von Position a nach Position b
bewegt wird. Ohne die Induktivität L würde der Strom nach dem OHMschen
Gesetzt gleich auf den stationären Wert I0 = U0 /R ansteigen, wobei U0 die
105
5.6 Der RL-Kreis
Abbildung 5.11: Ein- und Ausschaltvorgang beim RL-Kreis.
Spannung der Spannungsquelle ist. Infolge der Selbstinduktion entsteht in der
Spule jedoch eine Spannung, die nach der LENZschen Regel so gerichtet ist, das
sie dem Aufbau des magnetischen Flusses entgegenwirkt. Die am Widerstand
anliegende Spannung verringert sich dadurch von U0 auf
U0 + Uind = U0 − L
dI
.
dt
(5.30)
Die zeitliche Zunahme des Stroms dI/dt kann nach Gl. (5.30) den Wert U0 /L
nicht überschreiten und bleibt daher immer endlich. Wir berechnen nun den
genauen zeitlichen Verlauf des Stroms in dem RL-Kreis nach dem Einschalten
der Spannung U0 . Da über dem Widerstand R die Spannung in Gl. (5.30)
abfällt, gilt nach dem OHMschen Gesetz
U0 − L
bzw.
dI
= RI
dt
dI R
U0
+ I=
.
dt
L
L
(5.31)
Dies ist eine Differentialgleichung 1. Ordnung für die Funktion I(t). Eine direkte Methode, sie zu lösen, besteht in der Trennung der Variablen“. Aus
”
Gl. (5.31) folgt
R U0
− I dt
dI =
L R
106
5 Induktion
und damit
R
dI
dt .
U0 = −
L
I− R
Wir integrieren nun beide Seiten und berücksichtigen dabei die Anfangsbedingung, dass der Strom I zum Einschaltzeitpunkt t = 0 verschwindet, also
I(0) = 0. Das liefert
ZI
0
t
RZ
dI ′
=
−
dt′ ,
U0
′
L
I − R
(5.32)
0
wobei wir die Integrationsvariablen zur Unterscheidung von den Integrationsgrenzen mit einem Strich versehen haben. Die Berechnung der Integrale in
Gl. (5.32) liefert
!
I − UR0
R
ln
=− t .
U0
L
− R
Durch Anwenden der Exponentialfunktion auf beiden Seiten folgt
I−
U0 − R t
U0
=−
e L .
R
R
Und damit folgt schließlich
R
I(t) = I0 1 − e− L t
,
(5.33)
mit I0 = U0 /R. Der Strom nähert sich also asymptotisch dem Endwert
I0 = U0 /R, siehe Abb. (5.12a). Dabei spielt die Zeitkonstante des RL-Kreises
τ=
L
R
eine entscheidende Rolle. Aus Gl. (5.33) folgt I(τ )/I0 = 1 − 1/e ≈ 0, 63. Das
heißt, zur Zeit τ hat der Strom 63% des Endwertes erreicht. Diese Zeit wird
um so länger, je größer L und je kleiner R ist.
Als nächstes betrachten wir den Ausschaltvorgang, also die Situation, wenn
der Schalter in Abb. (5.11) von Position b wieder nach Position a bewegt wird.
Beim Ausschaltvorgang fällt der Strom nicht direkt auf Null ab, sondern infolge
der Selbstinduktion entsteht in der Spule eine Spannung, die so gerichtet ist,
dass der Abbau des magnetischen Flusses erschwert wird. Wir berechnen nun
den genauen zeitlichen Verlauf des Stroms für den Ausschaltvorgang. Nach
dem Abklemmen der Spannung U0 liegt nur noch die induzierte Spannung
Uind = −L dI/dt der Spule an dem Widerstand R an. Nach dem OHMschen
Gesetz gilt damit
dI
−L
= RI
dt
107
5.7 Die Energie des magnetischen Feldes
Abbildung 5.12: Der zeitliche Verlauf des Stroms in einem RL-Kreis beim Einschaltvorgang (a) und beim Ausschaltvorgang (b).
bzw.
dI
R
=− I .
(5.34)
dt
L
Auch diese Differentialgleichung kann man direkt mit der Methode der Trennung der Variablen lösen. Aus Gl. (5.34) folgt
R
dI
= − dt .
I
L
Integration beider Seiten unter Berücksichtigung der Anfangsbedingung
I(0) = I0 liefert
ZI
I0
t
RZ
dI ′
dt′
=
−
I′
L
0
und damit
I
R
=− t .
I0
L
Durch Anwenden der Exponentialfunktion auf beiden Seiten folgt
ln
R
I(t) = I0 e− L t .
(5.35)
Der Strom fällt also exponentiell auf Null ab, siehe Abb. (5.12b). Auch hier
tritt die Zeitkonstante τ = L/R auf. Aus Gl. (5.35) folgt I(τ )/I0 = 1/e ≈ 0, 37.
Das heißt, zur Zeit τ ist der Strom auf 37% des Anfangswertes gefallen.
5.7
Die Energie des magnetischen Feldes
Wir wollen nun den Einschaltstrom durch eine Induktivität L von einem Energiestandpunkt aus betrachten. Wir gehen davon aus, dass zu einem bestimmten Zeitpunkt der Strom i durch eine Induktivität L fließt, und dass dieser
108
5 Induktion
Strom weiter ansteigt. Das bewirkt in der Induktivität die induzierte Spannung Uind = −L di/dt. Um die weitere Ladung dq = i dt gegen diese Spannung
zu transportieren, muss die Arbeit
dW = − Uind dq = L
di
i dt = L i di
dt
aufgebracht werden. Um den Strom von i = 0 auf den Endwert i = I hochzufahren, ist insgesamt die Arbeit
W =
ZI
L i di =
0
1
L I2
2
(5.36)
notwendig. Durch den elektrischen Strom wird das Magnetfeld in der Induktivität aufgebaut, und es ist deshalb einleuchtend, davon auszugehen, dass die
aufgewandte Arbeit gemäß Gl. (5.36) als Energie in dem Magnetfeld steckt.
Wir betrachten nun speziell eine lange Spule. Die Länge l der Spule sei
sehr groß im Vergleich zu den Querabmessungen. Fließt durch die Spule der
Strom I, so entsteht gemäß Gl. (4.29) in ihrem Innern das homogene Magnetfeld
B = µ0 n I ,
(5.37)
wobei n die Wicklungsdichte der Spule ist, also die Anzahl der Wicklungen pro
Längeneinheit. Im Außenraum verschwindet das Magnetfeld. Nach Gl. (5.26)
ist die Induktivität einer langen Spule gegeben durch
L = µ 0 n2 A l ,
(5.38)
wobei A die Querschnittsfläche der Spule bezeichnet. Mit den Gln. (5.36),
(5.37) und (5.38) erhalten wir für die Energie des Magnetfeldes einer Spule
1
1
B2
B2
2
2
2
W = L I = µ0 n A l I =
Al =
V ,
2
2
2 µ0
2 µ0
wobei V = A l das Volumen des Raumes im Inneren der Spule ist, also
des Bereichs, wo das Magnetfeld existiert. Damit folgt für die Energiedichte wm = W/V des magnetischen Feldes in einer langen Spule
wm =
B2
.
2 µ0
(5.39)
Wir haben Gl. (5.39) hergeleitet für das Magnetfeld einer langen Spule. Es lässt
sich aber allgemein zeigen, dass die Energiedichte eines beliebigen Magnetfeldes
gegeben ist durch den Ausdruck in Gl. (5.39).
109
5.8 Materie im Magnetfeld
Die Gültigkeit der Formel in Gl. (5.36) können wir auch noch auf folgende
Weise einsehen. Wir betrachten dazu noch einmal den Ausschlaltvorgang in
einem RL-Kreis. Obwohl die Spannung zum Zeitpunkt t = 0 abgeschaltet wird,
fließt noch ein exponentiell abklingender Strom. Dieser hat gemäß Gl. (5.35)
die Form
R
I = I0 e− L t .
Dieser Strom verbraucht an dem Widerstand R pro Zeiteinheit die Energie
R
dW
= R I 2 = R I02 e−2 L t .
dt
Durch Integration erhält man daraus die gesamte am Widerstand geleistet
Arbeit (welche in Wärme umgewandelt wird) zu
W =
Z∞
0
=
Z∞
R
dW
R I02 e−2 L t dt
dt =
dt
R I02
0
Z∞
0
=
R
e−2 L t dt = R I02 −
L −2 R t
e L
2R
∞
0
1 2
LI .
2 0
Dies ist aber gemäß Gl. (5.36) gerade die gesamte im Magnetfeld der Induktivität gespeicherte Energie. Nach Abschalten der Spannung wird also das
Magnetfeld der Induktivität langsam abgebaut und die dabei frei werdende
Energie wird an dem Widerstand in Wärme umgewandelt.
5.8
Materie im Magnetfeld
Bei Materie in Magnetfeldern treten ähnliche Effekte auf, wie bei Materie
in elektrischen Feldern. Durch die Anwesenheit der Materie ändert sich das
Magnetfeld um den Faktor µ, also
~ = µB
~0 .
B
~ 0 das Magnetfeld im Vakuum und B
~ das Magnetfeld in der
Hierbei ist B
Materie. Der Faktor µ wird als Permeabilitätszahl oder relative Permeabilität bezeichnet. Im Gegensatz zu Dielektrika, die elektrische Felder immer
abschwächen, kann Materie Magnetfelder nicht nur schwächen, sondern auch
110
5 Induktion
verstärken, bei ferromagnetischen Materialien sogar erheblich. Im Einzelnen
unterscheidet man drei Fälle:
1. Diamagnetismus (µ < 1) Hier wird das Magnetfeld durch das Material
abgeschwächt. Der Grund dafür ist, dass auf atomarer Ebene Kreisströme induziert werden, die nach der LENZschen Regel ein Magnetfeld erzeugen, das
dem äußeren Feld entgegengerichtet ist und so eine Abschwächung des äußeren Feldes bewirkt. Dieser Effekt tritt bei allen Materialien auf, die erzeugten
magnetischen Momente sind aber nur klein. Wegen der geringen Größe wird
der Diamagnetismus bei Stoffen, deren Atome permanente magnetische Momente haben von anderen Effekten überlagert, die in den nachfolgenden Fällen
beschrieben werden.
2. Paramagnetismus (µ > 1) Im Gegensatz zu Diamagnetika haben paramagnetische Stoffe auf Grund der Bahnbewegung und des Spin der Elektronen
atomare magnetische Momente. Diese magnetischen Momente werden durch
ein äußeres Magnetfeld ausgerichtet, und das äußere Magnetfeld wird somit
verstärkt. Allerdings tritt eine nennenswerte Orientierung der magnetischen
Dipole nur bei sehr tiefen Temperaturen auf. Bei normalen Tempraturen ist
infolge der relativ hohen thermischen Energie nur ein geringer Teil der atomaren Dipole in Richtung des äußeren Feldes orientiert. Dabei nimmt der
Grad der atomaren Orientierung proportional mit wachsendem Magnetfeld
und umgekehrt proportional mit der Temperatur zu. Voraussetzung für dieses
paramagnetische Verhalten ist eine hinreichend kleine magnetische Wechselwirkung zwischen den einzelnen Dipolen, so dass die Wechselwirkungsenergie
viel kleiner als die thermische Energie der Dipole ist.
3. Ferromagnetismus (µ ≫ 1) Bei ferromagnetischen Stoffen, wie z.B.
Eisen, ist die Wechselwirkung zwischen benachbarten magnetischen Atomen
groß. Dadurch wird die parallele Ausrichtung aller magnetischen Dipole in
gewissen Bereichen erzwungen selbst ohne ein äußeres Feld. Erst beim Überschreiten einer bestimmten Temperatur, der CURIE-Temperatur, bricht die
spontane Kopplung und Ausrichtung der magnetischen Dipole zusammen, und
das Material wird paramagnetisch. Unterhalb der CURIE-Temperatur ist bei
ferromagnetischen Stoffen, auch wenn sie makroskopisch nicht magnetisch sind,
die spontane Magnetisierung lokal vorhanden. Sie wird makroskopisch nicht
beobachtet, da die atomaren Dipole nur über kleine Bereiche von größenordnungsmäßig 0, 01 mm Durchmesser parallel angeornet sind. Die Magnetisierungen dieser sogenannten WEISSschen Bezirke sind aber in einer nicht magnetisierten Probe statistisch orientiert, so dass die Gesamtmagnetisierung der
Probe verschwindet. Erst bei Anlegen eines äußeren Magnetfeldes ist eine makroskopische Magnetisierung der Probe zu beobachten, da die WEISSschen
Bezirke, deren spontane Magnetisierung parallel zu dem äußeren Feld gerich-
5.8 Materie im Magnetfeld
111
tet ist, auf Kosten der anderen Bezirke wachsen. Bei genügend hohem äußeren
Feld nähert sich die Magnetisierung der Probe der Sättigungsmagnetisierung.
In diesem Fall sind alle atomaren magnetischen Dipolmomente parallel ausgerichtet. Das bedeutet, dass bei Ferromagntika die Magnetisierung nicht proportional zu dem Magnetfeld ist. Tatsächlich zeigt die Magnetisierungskurve
einen sogenanntes Hystereseverhalten, siehe Abb. 5.13. Hier ist das Magnetfeld B in der Probe aufgetragen gegen das magnetisierende Feld B0 . Geht
Abbildung 5.13: Die Magnetisierungskurve B(B0 ) einer Weicheisenprobe.
man von einer nicht magnetisierten Probe aus, so folgt man bei Erhöhung des
magnetisierenden Feldes B0 der sog. Neukurve und erreicht bei hinreichend
großen Feldern die Sättigungsmagnetisierug. Verringert man nun B0 wieder,
so folgt man nicht mehr der Neukurve, sondern einer höher liegenden Kurve.
Insbesondere bleibt für B0 = 0 eine Restmagnetisierung, die sog. Remanenz .
Diese wird erst durch ein bestimmtes entgegengerichtetes Feld B0 , das man als
Koerzitivkraft bezeichnet, zum Verschwinden gebracht. Remanenz und Koerzitivkraft lassen sich durch besondere Behandlung und die Zusammensetzung
des Materials in weitem Bereich beeinflussen. So wird man für einen Dauermagneten eine große Remanenz und Koerzitivkraft fordern, während man
für einen Transformatorkern einen ferromagnetischen Werkstoff mit geringer
Hysterese verwenden wird.
112
5 Induktion
Kapitel 6
Elektromagnetische Wellen
6.1
Das AMPERE-MAXWELLsche Gesetz
Das AMPEREsche Gesetz (4.16) sagt aus, dass jeder Leitungsstrom I von
~ umgeben ist wobei gilt:
einem magnetischen Wirbelfeld B
I
~ d~r = µ0 I .
B
(6.1)
C
~ entlang der Kurve C, welche die Fläche A
Das heißt, das Kurvenintegral von B
berandet, ist proportional zu dem durch diese Fäche tretenden Strom. MAXWELL wies als erster darauf hin, dass das Gesetz in dieser Form schon bei einfachen Wechselstromkreisen mit einem Kondensator keine eindeutigen Werte
~ liefert, also zu Widersprüchen führt. Wie in Bild (6.1) dargestellt ist,
für B
endet nämlich der von links kommende Leitungsstrom auf der linken Kondensatorplatte. Legt man daher die Fläche, entlang deren Berandung nach dem
AMPEREsche Gesetz integriert werden soll, links von der linken Kondensatorplatte (Fläche A1 in Abb. 6.1), so geht der volle Leitungsstrom durch diese
~ einen Wert mit B
~ 6= 0 entlang der Berandung C.
Fläche und man erhält für B
Legt man dagegen für die gleiche Berandungskurve C die zugehörige Integrationsfläche rechts von der linken Kondensatorplatte (Fläche A2 in Abb. 6.1), so
~ im Kondensator, aber kein Leitungsstrom
tritt lediglich das elektrische Feld E
mehr durch sie hindurch, und das Magnetfeld wäre gemäß Gl. (6.1) Null. Dieser offensichtliche Widerspruch ist natürlich physikalisch unsinnig und zeigt,
dass das AMPEREsche Gesetz (6.1) noch einer Erweiterung bedarf.
Es ist nun nicht schwer herzuleiten, welche Erweiterung notwendig ist. Nach
Gl. (2.23) erzeugt eine Ladung Q auf dem Plattenkondensator der Fläche A ein
elektrisches Feld E zwischen den Kondensatorplatten, wobei gilt Q = ε0 A E.
113
114
6 Elektromagnetische Wellen
Abbildung 6.1: Das AMPEREsche Gesetz angewandt auf einen einfachen
Stromkreis mit Kondensator. Die Inegrationsfläche verläuft einmal außerhalb
(Fläche A1 ) und einmal innerhalb (Fläche A2 ) des Kondensators.
Der Leitungsstrom I = dQ/dt, der in den Kondensator fließt, ist folglich
I = ε0 A
dE
.
dt
(6.2)
Wenn wir daher auf der rechten Seite von Gl. (6.1) zu dem Leitungsstrom I
noch den von dem elektrischen Feld E abhängigen Term IV = ε0 A dE/dt, den
man auch Verschiebungsstrom nennt, addieren, so erhalten wir in Abb. 6.1
sowohl für die Integrationsfläche A1 als auch A2 den gleichen Wert für das Ma~ Dies gilt gemäß unserer Herleitung zunächst für den Plattenkongnetfeld B.
~ über der betrachteten Fläche konstant ist. Im allgemeinen
densator, bei dem E
enthält man den Verschiebungsstrom durch Integration über die Fläche A, also
d Z ~ ~
E dA .
I V = ε0
dt
(6.3)
A
Damit erhalten wir folgende Erweiterung des AMPEREsche Gesetz (6.1), die
zuerst von MAXWELL vorgeschlagen wurde:
I
C
d Z ~ ~
~
E dA .
B d~r = µ0 I + ε0 µ0
dt
(6.4)
A
Heute ist durch viele Beobachtungen bewiesen, dass obige Erweiterung richtig ist, d.h. nicht nur Leitungsströme, sondern auch zeitlich sich ändernde
115
6.2 Die MAXWELLschen Gleichungen
elektrische Felder können magnetische Felder hervorrufen. Insbesondere bei
der Ausbreitung von elektromagnetischen Wellen werden Magnetfelder durch
zeitlich veränderliche elektrische Felder erzeugt, so dass die Existenz elektromagnetischer Wellen als bester Beweis für die Richtigkeit des AMPEREMAXWELLschen Gesetzes (6.4) angesehen werden kann.
6.2
Die MAXWELLschen Gleichungen
Wir sind nun in der Lage die entscheidenden Gleichungen für die Berechnung
von elektromagnetischen Feldern zusammenzustellen. Das GAUSSsche Gesetz
für das elektrische Feld (1.44), das GAUSSsche Gesetz für das magnetische
Feld (4.14), das FARADAYsche Induktionsgesetz (5.4) und das AMPEREMAXWELLsche Gesetz (6.4) stellen eine vollständige Beschreibung des elektromagnetischen Feldes dar. Alle vier Gleichnungen zusammen werden auch
als MAXWELLsche Gleichungen bezeichnet. Sie sind hier noch eimal zusammengestellt:
I
~ dA
~ = Q ,
E
ε0
(6.5)
I
~ dA
~ = 0,
B
(6.6)
A
A
I
~ d~r = − d
E
dt
I
Z
~ d~r = µ0 I + ε0 µ0 d E
~ dA
~.
B
dt
C
C
Z
~ dA
~,
B
(6.7)
A
(6.8)
A
Wegen der zentralen Bedeutung dieser Gleichungen für die Elektrodynamik
seien die Aussagen der einzelnen Gleichungen im folgenden noch einmal kurz
zusammengefasst.
Gl. (6.5) ist das GAUSSsche Gesetz für das elektrische Feld. Es sagt aus,
dass der Fluß des elektrischen Feldes durch eine geschlossene Oberfläche A
proportional zu der Ladung Q ist, die sich in dem Volumen befindet, welches
von der Fläche A eingeschlossen wird. Man kann dies auch so formulieren:
Ladungen sind die Quellen des elektrischen Feldes.
Gl. (6.6) ist das GAUSSsche Gesetz für das magnetische Feld. Es sagt aus,
dass der Fluß des magnetischen Feldes durch eine geschlossene Oberfläche A
stets Null ist. Dies ist gleichbedeutend damit, dass keine magnetischen Ladungen existieren, oder anders ausgedrückt, das magnetische Feld ist quellenfrei.
116
6 Elektromagnetische Wellen
Gl. (6.7) ist das FARADAYsche Induktionsgesetz. Es sagt aus, dass das
Wegintegral des elektrischen Feldes entlang einer geschlossenen Kurve C proportional ist zu der zeitlichen Änderung des magnetischen Flusses durch eine
Fläche A, die von der Kurve C berandet wird. Ein zeitlich veränderliches magnetisches Feld erzeugt also ein elektrisches (Wirbel-)Feld.
Gl. (6.8) ist das AMPERE-MAXWELLsche Gesetz. Es sagt aus, dass das
Wegintegral des magnetischen Feldes entlang einer geschlossenen Kurve C
gleich der Summe zweier Terme ist. Der erste Term ist proportional zu dem
elektrischen Strom I, der durch eine Fläche A fließt, die von der Kurve C berandet wird. Der zweite Term ist proportional zu der zeitlichen Änderung des elektrischen Flusses durch die gleiche Fläche A. Ein magnetisches (Wirbel-)Feld
wird demnach hervorgerufen durch einen elektrischen Strom und durch ein
zeitlich veränderliches elektrisches Feld.
In der dritten und vierten MAXWELLschen Gleichung bezeichnet A eine
beliebige Fläche im Raum, die von der Kurve C berandet wird. Der Umlaufsinn der Kurve C und die Orientierung der Fläche A stehen immer in einem
Rechtsschraubensinn zueinander. Die MAXWELLschen Gleichungen (6.5) bis
(6.8) beschreiben elektromagnetische Felder im Vakuum. Das elektromagneti~ der elektrischen Feldstärke und durch
sche Feld wird dabei durch den Vektor E
~ des magnetischen Feldes vollständig beschrieben. Die zeitliche
den Vektor B
und räumliche Entwicklung dieser Felder ist dann bei vorgegebenen Ladungen
Q und Strömen I bestimmt durch die obigen vier MAXWELLschen Gleichungen. Für die Berechnung elektromagnetischer Felder in Materie nehmen die
MAXWELLschen Gleichungen eine leicht modifizierte Form an. Hier ist dann
noch die Polarisation und die Magnetisierung der Materie zu berücksichtigen.
Die Gleichungen (6.5) bis (6.8) sind die MAXWELLschen Gleichungen in Integralform. Man kann sie auch in differentieller Form schreiben, worauf wir
aber hier nicht eingehen wollen.
6.3
Grundlagen der Wellenausbreitung
Eine Wellenausbreitung wird beobachtet, wenn schwingungsfähige Systeme
räumlich miteinander gekoppelt sind. Durch die Kopplung kann sich die
Schwingung eines Systems auf die Nachbarn übertragen, was zu einer räumlichen Ausbreitung des Schwingungszustandes führt. In Abb. 6.2a ist eine Kette
von Fadenpendeln dargestellt, die über Schraubenfedern miteinander verbunden sind. Regt man das erste Pendel senkrecht zur x-Achse in s-Richtung zu
einer Schwingung an, so wird die erste Feder periodisch gedehnt und gestaucht,
so daß sie das zweite Pendel ebenfalls zu Schwingungen in s-Richtung anregt.
6.3 Grundlagen der Wellenausbreitung
117
Abbildung 6.2: Kette von Fadenpendeln, die über Schraubenfedern miteinander verbunden sind: a) System im Ruhezustand, b) Momentaufnahme“ einer
”
Transversalwelle, c) Momentaufnahme“ einer Longitudinalwelle
”
Die Anregung breitet sich auf diese Weise in x-Richtung aus, bis die ganze Kette schwingt. Die einzelnen Pendel schwingen mit einer zeitlichen Verzögerung,
denn die Auslenkung einer Feder wird erst eine kurze Zeit später am anderen
Ende der Feder wirksam. Auch die Masse der einzelnen Fadenpendel hat Einfluß darauf, wie schnell ein Pendel auf die Anregung durch seinen Vorgänger
reagiert. Der Schwingungszustand breitet sich also entlang der Kette mit einer charakteristischen Geschwindigkeit aus, die von der Federkonstante der
Kopplungsfedern und der Masse der Fadenpendel abhängt. In Abb. 6.2b ist
eine Momentaufnahme“ der entstehenden Welle dargestellt. Die Auslenkung
”
der Pendel wird durch die Größe s beschrieben. Sie hängt ab von dem Ort x,
an dem sich das jeweilige Pendel befindet, und von der Zeit t. s ist also eine
Funktion der zwei Variablen x und t, in Zeichen s = s(x, t).
Schwingen die Pendel, wie in Abb. 6.2b zu sehen, senkrecht zur Ausbreitungsrichtung, so spricht man von einer Transversalwelle. Schwingen die einzelnen Pendel in Ausbreitungsrichtung, x- und s-Achse sind dann parallel, so
spricht man von einer Longitudinalwelle. Eine solche Welle ergibt sich, wenn
das erste Pendel zu Schwingungen in x-Richtung angeregt wird. Abb. 6.2c
118
6 Elektromagnetische Wellen
zeigt eine Momentaufnahme“ einer Longitudinalwelle. Sie besteht aus einer
”
Folge von Verdichtungen und Verdünnungen, die sich mit einer bestimmten
Geschwindigkeit in x-Richtung ausbreiten.
Betrachtet man Wellen, die sich entlang einer Kette aus gekoppelten Pendeln ausbreiten, so ist deutlich zu sehen, daß bei der Ausbreitung einer Welle
keine Materie transportiert wird, sondern daß lediglich ein Schwingungszustand übertragen wird. Dies ist ein allgemeines Charakteristikum von Wellen.
Wir halten deshalb fest:
Bei der Ausbreitung einer Welle wird keine Materie transportiert,
dafür aber Energie.
Besteht das Medium, in dem sich die Welle ausbreitet, aus einzelnen Elementen (z.B. die Fadenpendel in Abb. 6.2), so spricht man von einem diskreten
System. Ist das welleleitende Medium demgegenüber eine Gas- oder Flüssigkeitssäule oder ein fester Stab, so spricht man von einem kontinuierlichen System. Auch ein Kontinuum besteht streng genommen aus einzelnen Oszillatoren, aber ihre Ausdehnung ist so gering, daß man sie gegen Null gehen lassen
kann. Man denkt sich die Masse und die elastische Eigenschaft des Materials
kontinuierlich verteilt. In Gasen und Flüssigkeiten ohne innere Reibung sind
lediglich Longitudinalwellen ausbreitungsfähig, da praktisch keine Querkräfte
übertragen werden können. In Festkörpern sind sowohl Longitudinal- als auch
Transversalwellen ausbreitungsfähig. Bei den Transversalwellen gibt es zwei
verschiedene Typen: die Scher- und die Torsionswellen. Longitudinalwellen in
Festkörpern, Flüssigkeiten oder Gasen werden auch als Schallwellen bezeichnet, da das menschliche Ohr diese Wellen in einem bestimmten Frequenzbereich
als Schall wahrnimmt.
Eine besondere Form von Transversalwellen sind die elektromagnetischen
Wellen. Bei ihnen schwingen der elektrische und der magnetische Feldstärkevektor senkrecht zur Ausbreitungsrichtung. Die elektromagnetischen Wellen
benötigen im Gegensatz zu den mechanischen Wellen kein Übertragungsmedium. Sie können sich auch im Vakuum ausbreiten. In einem bestimmten
Frequenzbereich werden diese Wellen vom menschlichen Auge als Licht wahrgenommen. Die Natur des Lichtes als elektromagnetische Transversalwelle wurde
zuerst von MAXWELL (1831 - 1879) erkannt.
Verbindet man bei einer sich räumlich ausbreitenden Welle benachbarte
Punkte mit gleichem Schwingungszustand (z.B. Maximum der Auslenkung)
miteinander, so erhält man bestimmte geometrische Flächen, die als Wellenflächen oder Wellenfronten bezeichnet werden. Die Form der Wellenflächen
hängt von der Geometrie des Erregers (Senders) der Welle sowie von den Eigenschaften des Übertragungsmediums ab. Von besonderer Bedeutung sind
6.3 Grundlagen der Wellenausbreitung
119
Kugelwellen, Zylinderwellen und ebene Wellen. Kugelwellen entstehen, wenn
punkt- oder kugelförmige Erreger Wellen aussenden. Die Wellenflächen sind in
diesem Fall konzentrische Kugelflächen um das Erregerzentrum. Beispielsweise
breitet sich nach der Zündung eines Knallkörpers eine kugelförmige Druckwelle
in der Luft aus. Sendet ein geradliniger oder zylinderförmiger Erreger radial
Wellen aus, so sind die Wellenflächen konzentrische Zylindermantelflächen, und
die entstehenden Wellen werden Zylinderwellen genannt. Ebene Wellen ergeben sich schließlich, wenn ein ausgedehnter ebener Strahler Wellen aussendet.
Ein Lautsprecher mit einer großen Membran gibt näherungsweise ebene Wellen ab. Ein Ausschnitt aus einer Kugel- bzw. Zylinderwelle kann in großem
Abstand vom Erregerzentrum als ebene Welle angesehen werden.
Wir betrachten im folgenden ungedämpfte Wellen, die sich in eine Raumrichtung ausbreiten mögen. Ansonsten kann es sich jedoch um ganz beliebige
Wellen handeln, longitudinal oder transversal, mechanisch oder elektromagnetisch, u.s.w. An einem bestimmten Ort sei die sich ändernde physikalische
Größe s (z.B. die Auslenkung des ersten Pendels in Abb. 6.2) als Funktion der
Zeit vorgegeben, etwa durch die Funktion f (t). Diese stellt die Anregung der
Welle dar, die an einem Ende des welleleitenden Mediums (ohne Einschränkung
der Allgemeinheit an der Stelle x = 0) erfolgen soll. Gesucht ist die Größe s an
einem beliebigen Ort x des welleleitenden Mediums zu einem beliebigen Zeitpunkt t. Eine Bedingung für die gesuchte Funktion s(x, t) ist gemäß obigem
s(0, t) = f (t) .
(6.9)
Wir setzen an dieser Stelle voraus, daß sich alle Werte der physikalischen
Größe s mit derselben Geschwindigkeit c, der sogenannten Ausbreitungs- oder
Phasengeschwindigkeit, ausbreiten. Die Phasengeschwindigkeit ist damit folgendermaßen definiert:
Definition 1 Bei einer Welle bezeichnet man den Quotienten aus dem Weg,
den ein bestimmter Schwingungszustand (z.B. ein Nulldurchgang oder ein Maximum der Auslenkung) zurücklegt, und der Zeit, die dafür benötigt wird, als
Phasengeschwindigkeit c.
Die Welle breite sich in positive x-Richtung aus. Ein bestimmter Wert der
physikalischen Größe s benötigt dann, um von x = 0 nach x zu kommen, die
Laufzeit τ = x/c. Das bedeutet, dasjenige s, welches zur Zeit t am Orte x
vorliegt, ist zur Zeit
x
t−τ =t−
(6.10)
c
120
6 Elektromagnetische Wellen
am Orte x = 0 gewesen. Mit den Gln. (6.9) und (6.10) folgt
x
x
=f t−
s(x, t) = s(0, t − τ ) = s 0, t −
c
c
.
Da wir für die Anregung der Welle eine beliebige Funktion f (t) zugelassen
hatten, erhalten wir somit das Ergebnis: Jede ungedämpfte, in positive xRichtung laufende Welle läßt sich in der Form
x
c
(6.11)
x
c
(6.12)
s(x, t) = f t −
darstellen. Entsprechend wird durch
s(x, t) = f t +
eine beliebige ungedämpfte, in negative x-Richtung laufende Welle dargestellt.
Ein besonders wichtiger Wellentyp ergibt sich, wenn die Anregung der Welle
durch eine harmonische Schwingung erfolgt. In diesem Fall hat die Funktion
f (t) die Form
f (t) = ŝ sin(ωt) .
Hierbei ist ŝ die Amplitude und ω = 2πf = 2π/T die Kreisfrequenz der Anregung, wobei f deren Frequenz und T deren Periodendauer ist. Die zugehörige
sich in positive x-Richtung ausbreitende harmonische Welle ist dann gemäß
Gl. (6.11) gegeben durch
x
s(x, t) = ŝ sin ω t −
c
.
(6.13)
Führt man durch λ = cT = c/f eine neue physikalische Größe ein, so läßt sich
die harmonische Welle auch in der Form
s(x, t) = ŝ sin 2π
t
x
−
T
λ
(6.14)
schreiben. In dieser Darstellung ist eine wichtige Eigenschaft einer harmonischen Welle gut zu erkennen. Die Auslenkung s(x, t) ist periodisch sowohl in
der Zeit t als auch in der Ortsvariablen x. Bei festem Ort x ist s als Funktion
der Zeit periodisch mit der Periodendauer T , und zu einer festen Zeit t ist s als
Funktion des Ortes periodisch mit der räumlichen Periode λ. Die Größe λ wird
als Wellenlänge der harmonischen Welle bezeichnet. Betrachten wir beispielsweise eine harmonische Welle, die sich entlang der in Abb. 6.2 dargestellten
Kette aus gekoppelten Pendeln ausbreitet, so liefert uns s(x, t) bei festem Ort x
121
6.3 Grundlagen der Wellenausbreitung
als Funktion der Zeit t ein Oszillogramm“ der Schwingung des Pendels an der
”
Stelle x, während uns s(x, t) bei fester Zeit t als Funktion von x eine Mo”
mentaufnahme“ der harmonischen Welle liefert, wie sie in diesem Augenblick
entlang der gesamten Kette wahrgenommen werden kann. In Abb. 6.3 sind
solche Momentaufnahmen für verschiedene Zeitpunkte dargestellt. Zwischen
s
6
-
t=0
x
s
6
-
t = T /4
x
s
6
-
t = T /2
x
λ
-
Abbildung 6.3: Momentaufnahmen“ einer harmonischen Welle zu verschiede”
nen Zeitpunkten
der Frequenz f , der Wellenlänge λ und der Phasengeschwindigkeit c besteht
der wichtige Zusammenhang
c = λf .
(6.15)
Wird also bei einer harmonischen Welle die Frequenz vorgegeben, so liegt die
Wellenlänge automatisch fest. Eine kleine Frequenz bedingt eine große Wellenlänge und umgekehrt. Eine dritte Darstellung einer harmonischen Welle
erhält man, wenn man analog zur Kreisfrequenz ω = 2π/T die Kreiswellenzahl k einführt durch k = 2π/λ. Die Kreiswellenzahl hat damit die Einheit
[k] = m−1 . Aus Gl. (6.14) folgt direkt
s(x, t) = ŝ sin(ωt − kx) .
(6.16)
122
6 Elektromagnetische Wellen
Die Beziehung c = λf läßt sich auch mit der Kreisfrequenz ω und der Kreiswellenzahl k formulieren. Es gilt
ω
c= .
(6.17)
k
Es sei noch einmal darauf hingewiesen, daß die in diesem Abschnitt durchgeführten Betrachtungen voraussetzen, daß die Wellenausbreitung verlustfrei
ist und nur in eine Raumrichtung erfolgt. Durch die Gleichung
s(x, t) = ŝ sin(ωt + kx)
wird analog zu Gl. (6.16) eine harmonische Welle beschrieben, die sich in negative x-Richtung ausbreitet.
Die harmonische Welle ist eine spezielle, in der Praxis jedoch sehr häufig
vorkommende Wellenform, da die Anregung einer Welle in vielen Fällen durch
eine harmonische Schwingung erfolgt. Die Hauptbedeutung der harmonischen
Welle besteht aber darin, daß sich jede beliebige Wellenform als Überlagerung
harmonischer Wellen darstellen läßt (FOURIER-Analyse).
Wellenausbreitung wird in der Physik allgemein durch folgende Gleichung
beschrieben:
2
∂ 2s
2∂ s
=
c
.
(6.18)
∂t2
∂x2
Diese Beziehung für s(x, t) wird als Wellengleichung bezeichnet. Wann immer
sich für eine physikalische Größe s obige Gleichung herleiten lässt, so ist für
diese Größe Wellenausbreitung möglich.
Man kann nämlich leicht nachprüfen, daß die harmonische Welle
x
s(x, t) = ŝ sin ω t −
c
(6.19)
eine Lösung der Wellengleichung ist. Wir berechnen dazu die ensprechenden
partiellen Ableitungen.
x
∂s
= ωŝ cos ω t −
∂t
c
∂ 2s
x
= −ω 2 ŝ sin ω t −
2
∂t
c
,
∂ 2s
ω2
x
=
−
ŝ sin ω t −
2
2
∂x
c
c
,
bzw.
∂s
ω
x
= − ŝ cos ω t −
∂x
c
c
,
.
Einsetzen dieser Ergebnisse in Gl. (6.18) liefert sofort, daß die harmonische
Welle (6.19) eine Lösung der Wellengleichung (6.18) ist, und man erkennt weiter, daß die Konstante c in Gl. (6.18) die Bedeutung der Phasengeschwindigkeit
hat.
6.4 Wellengleichung für das elektrische und magnetische Feld
123
Aber nicht nur die harmonische Welle s(x, t) = ŝ sin ω(t − x/c), sondern jede
Welle der Form
x
s(x, t) = f t −
c
ist Lösung der Wellengleichung (6.18), wobei f (ξ) eine beliebige, zweimal stetig differenzierbare Funktion ist. Durch Bilden der entsprechenden Ableitungen
und Einsetzen in Gl. (6.18) läßt sich dies direkt nachprüfen (Übungsaufgabe).
Das bedeutet, ganz beliebige Wellenprofile können sich in dem entsprechenden Medium ausbreiten, und alle haben die durch die Konstante c festgelegte
Ausbreitungsgeschwindigkeit.
6.4
Wellengleichung für das elektrische und
magnetische Feld
Wir wollen in diesem Kapitel zeigen, daß sich aus den MAXWELLschen Gleichungen die Existenz elektromagnetischer Wellen herleiten läßt. Die grundlegende Idee dabei ist, daß gemäß der dritten und vierten MAXWELLschen
Gleichung zeitlich veränderliche elektrische und magnetische Felder untrennbar
miteinander verbunden sind, sie erzeugen sich gegenseitig. Die Kombination
beider Prinzipien ermöglicht, wie wir sehen werden, die Ausbreitung elektromagnetischer Wellen. Wir betrachten einen Raumbereich, der weit entfernt ist
von den Ladungen Q und den Strömen I, die das elektromagnetische Feld erzeugen, d.h. in dem von uns betrachteten Raumbereich gilt Q = 0 und I = 0.
Die MAXWELLschen Gleichungen haben damit die Form:
I
~ dA
~ = 0,
E
(6.20)
I
~ dA
~ = 0,
B
(6.21)
A
A
I
~ d~r = − d
E
dt
I
Z
~ d~r = µ0 I + ε0 µ0 d E
~ dA
~.
B
dt
C
C
Z
~ dA
~,
B
(6.22)
A
(6.23)
A
Die Entfernung vom Sender der elektromagnetischen Welle soll groß sein verglichen mit den räumlichen Abmessungen des Senders. Wir können daher an~ und B
~ räumlich nur noch von einer Koordinate
nehmen, daß die Feldgrößen E
abhängen, die entlang einer geraden Linie vom Sender zum Beobachtungspunkt gemessen wird. Dies soll im folgenden die x-Koordinate sein. Anders
124
6 Elektromagnetische Wellen
ausgedrückt, wir gehen davon aus, das die elektromagnetische Welle in dem
betrachteten Bereich als ebene Welle angesehen werden kann. Weiter wollen wir
voraussetzen, daß sowohl das elektrische als auch das magnetische Feld linear
polarisiert ist. Die oben getroffenen Voraussetzungen lassen sich folgendermaßen zusammenfassen: Wir gehen von einem elektrischen Feld aus, das überall
im Raum parallel zur y-Achse ist und nur von einer räumlichen Koordinate,
der x-Koordinate, und der Zeit t abhängt, d.h.
~
E(x,
t) = Ey (x, t)~ey .
(6.24)
Wir gehen weiter von einem magnetischen Feld aus, das überall im Raum
parallel zur z-Achse ist und ebenfalls nur von der x-Koordinate und der Zeit t
abhängt, d.h.
~
B(x,
t) = Bz (x, t) ~ez .
(6.25)
Mit diesem Ansatz versuchen wir, die MAXWELLschen Gleichungen zu lösen,
und wollen sehen, welche Bedingungen sich für Ey (x, t) und Bz (x, t) ergeben.
Wir sind bei obigem Ansatz davon ausgegangen, dass das elektrische und das
magnetische Feld senkrecht zueinander und senkrecht zur Ausbreitungsrichtung stehen. Es läßt sich zeigen, daß dies allgemein gültig ist.
Wir wenden nun die dritte MAXWELLsche Gleichung, Gl. (6.22), auf eine
kleine quadratische Fläche in der x, y-Ebene und die sie berandende Kurve
an, siehe Abb. 6.4. Die berandende Kurve besteht aus den vier Wegstücken
y
6
y + dy
d~
r4
y
?
+
~
dA
z+
d~
r3
6
d~
r2
-
d~
r1
-
x
x + dx
x
Abbildung 6.4: Anwendung der dritten MAXWELLschen Gleichung auf ein
kleines Quadrat in der x, y-Ebene
d~r1 = dx ~ex , d~r2 = dy ~ey , d~r3 = −dx ~ex und d~r4 = −dy ~ey . Da die elektrische
Feldstärke senkrecht auf den Wegstücken d~r1 und d~r3 steht, tragen diese
zum Wegintegral nicht bei. Entlang des Wegstücks d~r2 ist die elektrische
125
6.4 Wellengleichung für das elektrische und magnetische Feld
~ + dx, t) = Ey (x + dx, t)~ey . EntFeldstärke konstant und hat den Wert E(x
lang des Wegstücks d~r4 ist die elektrische Feldstärke ebenfalls konstant und
~
hat den Wert E(x,
t) = Ey (x, t)~ey . Das Wegintegral auf der linken Seite der
dritten MAXWELLschen Gleichung ergibt sich damit zu
I
C
~ d~r = Ey (x + dx, t) − Ey (x, t) dy = ∂Ey dx dy .
E
∂x
Hierbei wurde für das elektrische Feld Ey (x + dx, t)
Reihenentwicklung bis zur ersten Ordnung benutzt:
Ey (x + dx, t) = Ey (x, t) +
eine
(6.26)
Taylor-
∂Ey
(x, t) dx .
∂x
Das quadratische Flächenstück wird beschrieben durch den Flächenvektor
~ = dx dy ~ez . Die Orientierung des Flächenvektors ist festgelegt durch die
dA
Bedingung, daß der Umlaufsinn der berandenden Kurve und die Orientierung
der Fläche in einem Rechtsschraubensinn zueinander stehen müssen. Da das
Quadrat infinitesimal klein ist, kann das magnetische Feld über dem ganzen
~
Quadrat als konstant angesehen werden mit dem Wert B(x,
t) = Bz (x, t)~ez .
Das Flächenintegral auf der rechten Seite der dritten MAXWELLschen Gleichung ergibt sich damit zu
I
~ dA
~ = Bz dx dy .
B
(6.27)
A
Setzt man die in den Gln. (6.26) und (6.27) gewonnenen Resultate in die dritte
MAXWELLsche Gleichung, Gl. (6.22), ein, so folgt
∂Ey
∂Bz
dx dy = −
dx dy
∂x
∂t
bzw. nach Division durch dx dy
∂Ey
∂Bz
=−
.
∂x
∂t
(6.28)
Als nächstes führen wir eine ganz ähnliche Betrachtung durch, wobei wir
diesmal die vierte MAXWELLsche Gleichung, Gl. (6.23), benutzen (beachte
I = 0). Wir wenden diese Gleichung an auf eine kleine quadratische Fläche
in der x, z-Ebene und die sie berandende Kurve, siehe Abb. 6.5. Die berandende Kurve besteht aus den vier Wegstücken d~r1 = −dx ~ex , d~r2 = dz ~ez ,
~ senkrecht auf den
d~r3 = dx ~ex und d~r4 = −dz ~ez . Da das magnetische Feld B
126
6 Elektromagnetische Wellen
y
6
~
dA
6x
z
d~
r2
z + dz
z
x
-
d~
r1
-
x + dx
d~
r4
d~
r3
Abbildung 6.5: Anwendung der vierten MAXWELLschen Gleichung auf ein
kleines Quadrat in der x, z-Ebene
Wegstücken d~r1 und d~r3 steht, tragen diese zum Wegintegral nicht bei. Entlang des Wegstücks d~r2 ist das magnetische Feld konstant und hat den Wert
~
B(x,
t) = Bz (x, t)~ez . Entlang des Wegstücks d~r4 ist das magnetische Feld eben~ + dx, t) = Bz (x + dx, t)~ez . Das Wegintefalls konstant und hat den Wert B(x
gral auf der linken Seite der vierten MAXWELLschen Gleichung ergibt sich
damit zu
I
~ d~r = Bz (x, t) − Bz (x + dx, t) dz = − ∂Bz dx dz .
B
(6.29)
∂x
C
Das quadratische Flächenstück wird beschrieben durch den in y-Richtung zei~ = dx dz ~ey . Da das Quadrat infinitesimal klein ist,
genden Flächenvektor dA
kann das elektrische Feld über dem ganzen Quadrat als konstant angesehen
~
werden mit dem Wert E(x,
t) = Ey (x, t)~ey . Das Flächenintegral auf der rechten
Seite der vierten MAXWELLschen Gleichung ergibt sich damit zu
I
~ dA
~ = Ey dx dz .
E
(6.30)
A
Setzt man die in den Gln. (6.29) und (6.30) gewonnenen Resultate in die vierte
MAXWELLsche Gleichung, Gl. (6.23), ein, so folgt
∂Bz
∂Ey
dx dz = ε0 µ0
dx dz
∂x
∂t
bzw. nach Division durch −dx dz
−
∂Bz
∂Ey
= −ε0 µ0
.
∂x
∂t
(6.31)
6.4 Wellengleichung für das elektrische und magnetische Feld
127
Durch geeignetes Zusammenfügen der Gln. (6.28) und (6.31) erhält man
die Wellengleichung für die Feldkomponenten Ey und Bz . Differenziert man
Gl. (6.28) nach x und Gl. (6.31) nach t, so ergibt sich
∂
∂ 2 Ey
=
−
∂x2
∂x
∂Bz
∂t
!
und
∂
∂t
∂Bz
∂x
!
= −ε0 µ0
∂ 2 Ey
.
∂t2
Setzen wir Ey und Bz als zweimal stetig differenzierbar voraus, so ist bei den
gemischten partiellen Ableitungen die Reihenfolge unerheblich, und aus den
obigen beiden Gleichungen folgt
∂ 2 Ey
∂ 2 Ey
=
ε
µ
.
0
0
∂x2
∂t2
(6.32)
Differenziert man Gl. (6.31) nach x und Gl. (6.28) nach t, so erhält man
ganz ähnlich wie oben
∂ 2 Bz
∂ 2 Bz
=
ε
µ
.
(6.33)
0
0
∂x2
∂t2
Gl. (6.32) bzw. (6.33) ist die Wellengleichung für Ey bzw. Bz . Wir haben bei obiger Herleitung lediglich die dritte und vierte MAXWELLsche Gleichung benutzt. Man kann aber zeigen, daß bei unserem Ansatz, Gl. (6.24) und
(6.25), die ersten beiden MAXWELLschen Gleichungen automatisch erfüllt
sind (Übungsaufgabe). Durch Vergleich mit der allgemeinen Form der Wellengleichung ∂ 2 s/∂t2 = c2 ∂ 2 s/∂x2 ergibt sich, daß für die Ausbreitungsgeschwindigkeit (Phasengeschwindigkeit) elektromagnetischer Wellen im Vakuum c2 = 1/ε0 µ0 gilt oder
1
c= √
.
(6.34)
ε0 µ0
Setzt man in diese Gleichung die Zahlenwerte für die elektrische Feldkonstante ε0 und die magnetische Feldkonstante µ0 ein, so erhält man für c den
Wert der Lichtgeschwindigkeit im Vakuum. Das legt die Vermutung nahe, daß
Licht eine elektromagnetische Welle ist, was zuerst von MAXWELL erkannt
wurde. Im heute verwendeten Internationalen Einheitensystem (SI) spielt
Gl. (6.34) eine wichtige Rolle. Durch die Definition der Einheit für die elektrische Stromstärke (Ampere) wird die magnetische Feldkonstante auf den Wert
µ0 = 4π · 10−7 N A−2 festgesetzt. Für die Lichtgeschwindigkeit im Vakuum ist
der Wert c = 299 792 458 m s−1 festgesetzt. Der Wert für die elektrische Feldkonstante ergibt sich dann mit Gl. (6.34) zu ε0 = 8, 854187817 . . . 10−12 F m−1 .
Breitet sich die elektromagnetische Welle nicht im Vakuum, sondern in einem
Material mit der Dielektrizitätszahl ε und der Permeabilitätszahl µ aus, dann
128
6 Elektromagnetische Wellen
ist die Ausbreitungsgeschwindigkeit der Welle gegeben durch
c= √
1
.
εε0 µµ0
Dies ist auch die Lichtgeschwindigkeit in dem entsprechenden Material.
Wie wir wissen, ist insbesondere die harmonische Welle eine Lösung der Wellengleichung. Eine mögliche Form einer elektromagnetischen Welle, wie man
sie z.B. im Fernfeld einer Dipolantenne findet, ist somit gegeben durch
Ey = Ê sin(ωt − kx) ,
(6.35)
Bz = B̂ sin(ωt − kx) ,
(6.36)
wobei die Kreisfrequenz ω und die Kreiswellenzahl k der Beziehung c = ω/k
genügen müssen. Die Amplituden Ê und B̂ zeigen eine gegenseitige Abhängigkeit, die man bestimmen kann, wenn man die obigen Ausdrücke für Ey und
Bz in die Gl. (6.28) einsetzt. Es ergibt sich
−k Ê cos(ωt − kx) = −ω B̂ cos(ωt − kx)
und damit
Ê = cB̂ .
(6.37)
Für die Felder Ey und Bz selbst gilt dann ebenfalls der Zusammenhang
Ey = cBz .
y
6
?
z
(6.38)
?
~
6 E
6 6
? ~
B
?
?
6
6
? 6
?
?
6
6
? 6
-
x
Abbildung 6.6: Darstellung einer harmonischen, linear polarisierten, elektromagnetischen Welle
6.4 Wellengleichung für das elektrische und magnetische Feld
129
Da das elektrische Feld und das magnetische Feld räumlich nur von x
abhängen, also für feste Zeit t konstant sind auf Ebenen senkrecht zur Ausbrei-
λ/m
104
103
102
101
100
10−1
10−2
10−3
10−4
10−5
10−6
10−7
10−8
10−9
10−10
10−11
10−12
10−13
f /Hz
104
105
Langwellen
106
Mittelwellen
107
Kurzwellen
108
Ultrakurzwellen
109
1010
1012
1013
380
420
480
560
580
640
. . . 420
. . . 480
. . . 560
. . . 580
. . . 640
. . . 780
Infrarot
1014
1015
sichtbares Licht
1016
Ultraviolett
1017
1018
Röntgenstrahlen
1019
γ-Strahlen
1020
1021
λ/nm
ca.
ca.
ca.
ca.
ca.
ca.
Mikrowellen
1011
ca.
ca.
ca.
ca.
ca.
ca.
f /THz
Spektralfarbe
790
710
620
540
520
470
Violett
Blau
Grün
Gelb
Orange
Rot
. . . 710
. . . 620
. . . 540
. . . 520
. . . 470
. . . 390
Abbildung 6.7: Einteilung der elektromagnetischen Wellen nach Wellenlänge
und Frequenz
130
6 Elektromagnetische Wellen
tungsrichtung, ist die oben beschriebene elektromagnetische Welle eine ebene
Welle. In Abb. 6.6 ist eine Momentaufnahme dieser elektromagnetischen Welle
dargestellt.
Elektromagnetische Wellen kommen mit Frequenzen f zwischen einigen Hz
und 1024 Hz vor. Das gesamte Frequenzspektrum ist in Abb. 6.7 dargestellt.
Neben den Frequenzen sind auch die zugehörigen Wellenlängen λ in Vakuum angegeben. Der Zusammenhang zwischen der Frequenz f und der Wellenlänge λ ist gegeben durch c = λf , wobei c die Lichtgeschwindigkeit im Vakuum ist. Das sichtbare Licht umfaßt den Wellenlängenbereich von ca. 380 nm
bis ca. 780 nm.
6.5
Energiedichte und Intensität einer elektromagnetischen Welle
Wie bei allen Wellen wird auch durch eine elektromagnetische Welle Energie
transportiert. In vorausgegangenen Kapiteln haben wir gezeigt, daß für die
Energiedichte we des elektrischen Feldes we = (1/2)ε0 E 2 und für die Energiedichte wm des magnetischen Feldes wm = (1/2µ0 )B 2 gilt. Die Energiedichte w
eines elektromagnetischen Feldes setzt sich aus diesen beiden Anteilen zusammen, d.h. es gilt
1
1 2
w = w e + w m = ε0 E 2 +
B .
2
2µ0
Wir werden nun zeigen, daß für eine harmonische elektromagnetische Welle
die Energiedichten wm und we gleich sind, was allgemein für ebene elektromagnetische Wellen gültig ist. Mit den Beziehungen Ey = cBz und c2 = 1/ε0 µ0
ergibt sich
wm =
1 2
1 2
1
ε0 2 ε0 2
2
E = E = we ,
B =
Bz =
(cB
)
=
z
2µ0
2µ0
2µ0 c2
2 y
2
also wm = we . Damit läßt sich die Energiedichte w schreiben in der Form
w = we + wm = 2we = ε0 Ey2 .
(6.39)
Nachdem wir die Energiedichte w bestimmt haben, läßt sich auch die Intensität S einer elektomagnetischen Welle berechnen. Die Intensität S einer
Welle ist dabei allgemein definiert durch:
Definition 2 Bei einer Welle wird der Quotient aus der Leistung P , die durch
die Fläche A transportiert wird, und der Fläche A selbst, welche senkrecht zur
6.5 Energiedichte und Intensität einer elektromagnetischen Welle
131
Ausbreitungsrichtung der Welle steht, als Energiestromdichte oder Intensität S
bezeichnet, in Zeichen
P
.
(6.40)
S=
A
In der Zeit dt wird die Energie dE = wAc dt durch eine Fläche A senkrecht
zur Ausbreitungsrichtung der Welle transportiert. Damit ergibt sich für die
durch die Fläche A transportierte Leistung P
P =
dE
= wAc .
dt
(6.41)
Mit Gl. (6.40) und (6.41) erhält man folgenden Zusammenhang zwischen
der Intensität S und der Energiedichte w einer Welle
S = wc .
(6.42)
Dieser Zusammenhang gilt nicht nur für mechanische Wellen, sondern allgemein, da in seine Herleitung keine nur mechanische Wellen betreffenden Beziehungen eingehen.
Aus S = wc folgt mit Gl. (6.39) und Ey = cBz
S = wc = ε0 cEy2 = ε0 c2 Ey Bz =
1
Ey Bz .
µ0
(6.43)
~ = Ey~ey und B
~ = Bz~ez gilt
Wegen E
~ ×B
~ = Ey Bz~ex .
E
Die rechte Seite in Gl. (6.43) läßt sich somit auffassen als der Betrag des
Vektors
~= 1E
~ ×B
~ .
S
(6.44)
µ0
Dieser Vektor wird als POYNTING-Vektor bezeichnet nach J. H. POYNTING
~ gibt offensichtlich die Intensität einer elektro(1852 - 1914). Der Betrag von S
~ gibt die Richtung an, in die
magnetischen Welle an, und die Richtung von S
sich eine elektromagnetische Welle ausbreitet.
Im Fall einer harmonischen Welle, beschrieben durch die Gln. (6.35) und
(6.36), erhält man mit Hilfe von Gl. (6.43) für die Intensität S
S=
1
1
Ey Bz = Ê B̂ sin2 (ωt − kx) .
µ0
µ0
(6.45)
Man erkennt, daß die Intensität periodisch von der Zeit abhängt. Das Zeitintervall, über welchem die Intensität einer elektromagnetischen Welle gemessen
132
6 Elektromagnetische Wellen
wird, ist in der Regel sehr viel länger als die Periodendauer T = 1/f der Welle.
Bei Lichtwellen liegt die Frequenz f z.B. in der Größenordnung von 5 · 1014 Hz.
Zum Vergleich mit experimentellen Ergebnissen ist deshalb die mittlere Intensität S von Interesse. Mit Gl. (6.45) läßt sie sich berechnen zu
S=
wobei
sin2 (ωt − kx) =
1
Ê B̂ ,
2µ0
(6.46)
1ZT
1
sin2 (ωt − kx) dt =
T 0
2
benutzt wurde. Mit den Beziehungen Ê = cB̂ und c2 = 1/ε0 µ0 läßt sich die
mittlere Intensität auch auf folgende Weisen schreiben
1
c 2
S = ε0 cÊ 2 =
B̂ .
2
2µ0
(6.47)
Die mittlere Intensität ist also proportional zum Quadrat der Amplitude Ê
bzw. B̂ der elektromagnetischen Welle.
Kapitel 7
Geometrische Optik
7.1
Das HUYGENSsche Prinzip
Die Optik beschreibt das Verhalten und die Eigenschaften des Lichtes. Die
Auffassung über die Natur des Lichtes änderte sich mehrmals in der Geschichte der Physik. Von NEWTON wurde 1672 eine Korpuskulartheorie entwickelt.
Ihr zufolge sendet eine Lichtquelle kleine Teilchen aus, die sich mit großer Geschwindigkeit ausbreiten. Die Phänomene der Beugung und Interferenz konnten aber nur mit der zuerst von HUYGENS 1678 entwickelten Wellentheorie
des Lichtes erklärt werden. Dabei wurde allgemein angenommen, daß es sich bei
Licht um elastische Longitudinalwellen handelt, die sich in einem den ganzen
Raum erfüllenden Medium, Äther genannt, ausbreiten. Nach der Entdeckung
der Polarisation wurde von FRESNEL 1815 der Schluß gezogen, daß Licht eine
Transversalwelle sein muß. Die Natur der Lichtwellen als elektromagnetische
Transversalwellen wurde schließlich 1865 von MAXWELL erkannt. Durch das
Experiment von MICHELSON und MORLEY 1887 wurde die Existenz eines
Äthers ausgeschlossen. Elektromagnetische Wellen, insbesondere Lichtwellen,
benötigen demzufolge kein Übertragungsmedium und können sich auch im Vakuum ausbreiten.
Bei der Beschreibung der Ausbreitung von Wellen haben wir bislang immer
ein homogenes Medium vorausgesetzt. Dies ist aber nicht mehr gegeben, wenn
eine Welle z.B. auf die Grenzfläche zwischen zwei unterschiedlichen Medien
oder eine begrenzende Öffnung oder ein sonstiges Hindernis trifft. Die Ausbreitung von Wellen unter diesen Bedingungen liesse sich im Prinzip zwar durch
Lösen der Wellengleichung berechnen, der Aufwand wäre aber sehr hoch. Hier
ist das HUYGENSsche Prinzip sehr hilfreich, welches der holländische Physiker
C. HUYGENS 1690 formulierte, um die Ausbreitung von Licht zu beschreiben.
Es lautet:
133
134
7 Geometrische Optik
Jeder Punkt auf einer primären Wellenfläche kann als Ursprung von
kugelförmigen sekundären Elementarwellen angesehen werden. Die
primäre Wellenfront zu einem späteren Zeitpunkt ergibt sich als
gemeinsame Einhüllende dieser Elementarwellen. Die sekundären
Elementarwellen schreiten mit einer Geschwindigkeit und Frequenz
fort, die gleich denen der Primärwelle in dem entsprechenden Punkt
des Raumes sind.
Im Rahmen einer Beugungstheorie, die auf der exakten Lösung der Wellengleichung beruht, konnte G. R. KIRCHHOFF (1824 - 1887) eine strenge mathematische Rechtfertigung des HUYGENSschen Prinzips geben. Dabei ergab
sich noch eine wichtige Ergänzung, deren Notwendigkeit man leicht einsehen
kann. Würden sich die sekundären Elementarwellen wirklich als Kugelwellen
gleichmäßig in alle Richtungen ausbereiten, so würde sich z.B. bei einer nach
rechts laufenden ebenen Welle als gemeinsame Einhüllende der Elementarwellen in Rückwärtsrichtung eine nach links wandernde, rückläufige Welle ergeben, die in der Realität natürlich nicht beobachtet wird. Die KIRCHHOFFsche
Beugungstheorie zeigt nun, daß die sekundären Elementarwellen mit einer bestimmten Richtungscharakteristik abgestrahlt werden. Wir werden das beim
Anwenden des HUYGENSschen Prinzips dadurch berücksichtigen, daß wir lediglich die Einhüllende in Ausbreitungsrichtung betrachten.
7.2
Prämisse der geometrischen Optik
Besonders in der Optik spricht man im Zusammenhang mit der Ausbreitung
von Wellen häufig von Strahlen bzw. Lichtstrahlen. Ein Strahl ist in der Physik
allgemein eine Trajektorie, die orthogonal zu den Wellenflächen verläuft. Das
heißt, ein Strahl ist eine Linie, die in jedem Schnittpunkt mit einer Wellenfläche senkrecht auf der Wellenfläche steht. Ein Strahl zeigt in die Richtung, in
die sich die Welle ausbreitet. Eine ebene Welle ist demzufolge ein Bündel paralleler Strahlen, während eine Kugelwelle einem radial vom Erregungszentrum
nach außen zeigenden Bündel divergenter Strahlen entspricht. Die geometrische
Optik oder Strahlenoptik fußt auf der Prämisse:
Im homogenen Medium breiten sich Lichtstrahlen geradlinig aus.
Dies ist aber nur dann der Fall, wenn die räumlichen Abmessungen sämtlicher Objekte, die die Ausbreitung des Lichtes beeinflussen, wie z.B. Blenden,
Linsen oder Spiegel, groß sind im Vergleich zur Wellenlänge des verwendeten Lichtes. Ansonsten treten Beugungseffekte auf, die ein Abweichen von der
7.2 Prämisse der geometrischen Optik
135
Abbildung 7.1: Erzeugung eines Bildes mit Hilfe einer Lochkamera. Man beachte die Veränderung der Bildschärfe, wenn der Lochdurchmesser abnimmt.
(Photos mit freundlicher Genehmigung von Dr. N. Joel, UNESCO)
136
7 Geometrische Optik
geradlinigen Ausbreitung der Lichtstrahlen bewirken. Der oben beschriebene
Sachverhalt läßt sich sehr deutlich beim Erzeugen eines Bildes mit Hilfe einer
Lochkamera sichtbar machen. Eine solche Kamera besteht aus einem Kasten,
bei dem sich in einer Seite ein sehr kleines Loch befindet, siehe Abb. 7.1. Wird
nun ein beleuchteter Gegenstand vor diese Kamera gebracht, so erzeugen alle
von dem Gegenstand ausgehenden Strahlen auf der dem Loch gegenüberliegenden Wand ein Bild. Allerdings entspricht jedem Punkt des Gegenstandes
nicht genau ein Bildpunkt, sondern ein Fleck, dessen Größe proportional zum
Durchmesser des Lochs ist. Dies führt dazu, daß das entstehende Bild unscharf
ist. Man könnte nun annehmen, daß das erzeugte Bild immer schärfer wird, je
kleiner man das Loch macht. Dies ist zunächst auch der Fall; wird der Durchmesser des Lochs aber vergleichbar mit der Wellenlänge des Lichtes, so wird
das entstehende Bild wieder unschärfer, siehe Abb. 7.1. In diesem Bereich beginnen Beugungseffekte aufzutreten, und es zeigt sich eine Abweichung von der
geradlinigen Ausbreitung der Strahlen. Das Phänomen der Beugung läßt sich
nur erklären, wenn man die Wellennatur des Lichtes berücksichtigt und die
Ausbreitung von Wellen mit dem HUYGENSschen Prinzip beschreibt. Trifft
z.B. eine ebene Welle auf eine begrenzende Öffnung, so kann nach dem HUYGENSschen Prinzip jeder Punkt einer Wellenfläche, die in die Öffnung gelangt,
als Ausgangspunkt von kugelförmigen Elementarwellen angesehen werden. Damit ist klar, daß Wellen auch in den geometrischen Schattenraum“ gelangen.
”
Eine ausführliche Darstellung der Beugung ist in Kapitel 8 gegeben.
Wir setzen also im folgenden voraus, daß die räumlichen Abmessungen aller
Objekte, die die Ausbreitung des Lichtes beeinflussen, groß sind im Vergleich
zur Wellenlänge. Die in diesem Kapitel gewonnenen Resultate gelten nicht nur
für Lichtwellen, sondern für beliebige Wellentypen.
7.3
Reflexion und Brechung
Das Phänomen der Reflexion und der Brechung tritt allgemein auf, wenn eine
Welle auf eine ebene Grenzfläche zwischen zwei verschiedenen Medien trifft.
Am einfachsten läßt sich dies bei der Ausbreitung von Licht sichtbar machen,
siehe Abb. 7.2. Trifft ein Lichtstrahl auf eine ebene Grenzfläche zwischen zwei
unterschiedlichen Medien 1 und 2, so wird er aufgespalten in einen reflektierten Strahl, der in das Medium 1 zurückgeht, und einen gebrochenen Strahl,
der durch die Grenzfläche in das Medium 2 eindringt. Dabei spielen Form
und Beschaffenheit der Grenzfläche eine wichtige Rolle. Sind die linearen Abmessungen der Unebenheiten der Grenzfläche größer als die Wellenlänge des
verwendeten Lichtes, so ergibt sich die diffuse Reflexion. Dabei wird ein auf
137
7.3 Reflexion und Brechung
einfallender
Strahl
@
@
R
@
reflektierter
Strahl
θ1 θ1r
n1
n2
A
A
θ2A
A
A
A
AAU
gebrochener
Strahl
Abbildung 7.2: Reflexion und Brechung von Licht an einer ebenen Grenzfläche
die Grenzfläche treffendes Bündel paralleler Lichtstrahlen in viele Richtungen
reflektiert. Aus diesem Grund sind viele Gegenstände aus allen Richtungen
(fast) gleich gut zu sehen. Sind die linearen Abmessungen der Unebenheiten
der Grenzfläche kleiner als die Wellenlänge des verwendeten Lichtes, wie es
z.B. bei ebenen Glasplatten, polierten Metalloberflächen oder ruhigen Flüssigkeitsoberflächen der Fall ist, so zeigt sich die spiegelnde Reflexion. Dabei wird
ein auf die Grenzfläche treffendes Bündel paralleler Lichtstrahlen in nur eine
Richtung reflektiert. Wir befassen uns im folgenden nur mit der spiegelnden
Reflexion, nehmen also an, daß die Grenzfläche hinreichend planar ist.
Die Normale in einem Punkt der Grenzfläche, der von einem Strahl getroffen wird, wird als Einfallslot bezeichnet, siehe Abb. 7.2. Der Winkel θ1
zwischen dem einfallenden Strahl und dem Einfallslot wird als Einfallswinkel
und der Winkel θ1r zwischen dem reflektierten Strahl und dem Einfallslot als
Reflexionswinkel bezeichnet. Für die Richtung des reflektierten Strahls gilt ein
einfaches Gesetz, das Reflexionsgesetz :
Einfallender Strahl, reflektierter Strahl und Einfallslot liegen in einer Ebene. Der Einfallswinkel θ1 und der Reflexionswinkel θ1r sind
gleich, in Zeichen
θ1 = θ1r .
(7.1)
Das Reflexionsgesetz wurde schon 300 v. Chr. von EUKLID gefunden. Der
Winkel θ2 zwischen dem in das Medium 2 eindringenden gebrochenen Strahl
und dem Einfallslot wird als Brechungswinkel bezeichnet. Der Zusammenhang zwischen dem Einfallswinkel und dem Brechungswinkel wurde von dem
138
7 Geometrische Optik
holländischen Mathematiker W. SNELLIUS (1591 - 1626) im Jahr 1620 gefunden. Das SNELLIUSsche Brechungsgesetz lautet:
Einfallender Strahl, gebrochener Strahl und Einfallslot liegen in
einer Ebene. Das Verhältnis zwischen dem Sinus des Einfallswinkels θ1 und dem Sinus des Brechungsswinkels θ2 ist konstant, und
zwar gilt
n2
sin θ1
=
.
(7.2)
sin θ2
n1
Hierbei sind n1 bzw. n2 zwei dimensionslose Konstanten, die eine Materialeigenschaft des Mediums 1 bzw. 2 beschreiben. n wird Brechungsindex genannt und ist eng mit der Lichtgeschwindigkeit c in dem jeweiligen Medium
verknüpft. Die genaue Definition von n ist weiter unten gegeben.
Wir wollen nun das Reflexionsgesetz und das SNELLIUSsche Brechungsgesetz aus dem HUYGENSschen Prinzip herleiten. Wir betrachten dazu eine
ebene Welle, die unter dem Winkel θ1 gegenüber dem Einfallslot auf eine planare Grenzfläche trifft, siehe Abb. 7.3. Die Ausbreitungsgeschwindigkeit der
B
B
B
B
B
B
D
B θ1 θ1r
B
B B BN
A
B
B
θ1
B
B
B
B
B
B
B
B BN
B
B
B
θ1r
B
B
BE
B
B θ1 θ1r
B
B B BN
C
Abbildung 7.3: Zur Herleitung des Reflexionsgesetzes aus dem HUYGENSschen Prinzip
Welle in den beiden aneinandergrenzenden Medien sei unterschiedlich (c1 bzw.
c2 ). Wir gehen von der Wellenfront AE aus, die die Grenzfläche zur Zeit t = 0
in dem Punkt A berühren möge. Den Punkt B der Grenzfläche erreicht die
Wellenfront zur Zeit t = τ und, wenn AB = BC gilt, den Punkt C zur Zeit
139
7.3 Reflexion und Brechung
t = 2τ . Die zu den Zeitpunkten t = 0, t = τ und t = 2τ jeweils von den Punkten A, B und C ausgehenden Elementarwellen breiten sich sowohl in dem
Medium 1 als auch in dem Medium 2 aus, allerdings mit den unterschiedlichen
Geschwindigkeiten c1 bzw. c2 .
Wir betrachten zunächst die Anteile der Elementarwellen, die sich im Medium 1 ausbreiteten, siehe Abb. 7.3. Die zur Zeit t = 0 von A ausgehende
Elementarwelle hat sich im Medium 1 zum Zeitpunkt t = 2τ auf den Radius
c1 2τ ausgedehnt, während die Elementarwelle, die zur Zeit t = τ von B ausging, zur Zeit t = 2τ den Radius c1 τ hat. Die von C zur Zeit t = 2τ ausgehende
Welle hat noch den Radius Null. Alle anderen (nicht eingezeichneten) Elementarwellen, die von den Punkten zwischen A und C ausgehen, haben zur Zeit
t = 2τ als Radien entsprechende Zwischenwerte, und zwar so, daß sich als gemeinsame Einhüllende (Tangente) die Wellenfront DC der reflektierten Welle
ergibt. Der Einfallswinkel θ1 ist der Winkel, den die einfallenden (parallelen)
Strahlen mit dem Einfallslot bilden. Aus Abb. 7.3 folgt, daß der Winkel θ1
identisch ist mit 6 EAC zwischen der Wellenfläche AE und der ebenen Grenzfläche. Die einfallende Welle legt in der Zeit 2τ die Strecke EC = c1 2τ zurück.
Damit läßt sich aus dem rechtwinkligen Dreieck ACE die Beziehung
sin θ1 =
EC
c1 2τ
=
AC
AC
(7.3)
ablesen. Der Reflexionswinkel θ1r ist der Winkel, den die reflektierten (parallelen) Strahlen mit dem Einfallslot bilden. Aus Abb. 7.3 folgt, daß der Winkel θ1r
identisch ist mit 6 ACD zwischen der Wellenfläche DC der reflektierten Welle
und der ebenen Grenzfläche. Da die Strecke AD = c1 2τ als Kugelradius der
von A ausgehenden Elementarwelle senkrecht auf der Einhüllenden DC steht,
ergibt sich aus dem rechtwinkligen Dreieck ACD
sin θ1r =
AD
c1 2τ
=
.
AC
AC
(7.4)
Aus den Gln. (7.3) und (7.4) folgt sin θ1 = sin θ1r , bzw.
θ1 = θ1r .
(7.5)
Dies ist das Reflexionsgesetz, siehe Gl. (7.1).
Als nächstes wollen wir das SNELLIUSsche Brechungsgesetz aus dem HUYGENSschen Prinzip herleiten. Wir betrachten dazu die Anteile der Elementarwellen, die sich in dem Medium 2 ausbreiteten, siehe Abb. 7.4. Die zur Zeit
t = 0 von A ausgehende Elementarwelle hat sich im Medium 2 zum Zeitpunkt
t = 2τ auf den Radius c2 2τ ausgedehnt, während die Elementarwelle, die zur
140
7 Geometrische Optik
A
A
A
A
A
A
A
A
A
A θ1
A
AA
U
AB
A
A
A
A
A
A
A
θ1
B
B
θ2BB
B
FB
B
B
B
BN
A
AAU B
B
B
B
B
AE
A
A
A
θ2
B
B
A
A
A θ1
A
AAU C
B
B
B
B
θ2 B
B
B
B
B
BN
B
B
B
B
B
BN
Abbildung 7.4: Zur Herleitung des SNELLIUSschen Brechungsgesetzes aus
dem HUYGENSschen Prinzip
Zeit t = τ von B ausging, im Medium 2 zur Zeit t = 2τ den Radius c2 τ hat.
Die von C zur Zeit t = 2τ ausgehende Welle hat noch den Radius Null. Alle
anderen (nicht eingezeichneten) Elementarwellen, die von den Punkten zwischen A und C ausgehen, haben zur Zeit t = 2τ als Radien entsprechende
Zwischenwerte, und zwar so, daß sich als gemeinsame Einhüllende (Tangente)
die Wellenfront F C der im Medium 2 fortschreitenden Welle ergibt. Der Brechungswinkel θ2 ist der Winkel, den die gebrochenen (parallelen) Strahlen mit
dem Einfallslot bilden. Aus Abb. 7.4 folgt, daß der Winkel θ2 identisch ist mit
6 ACF zwischen der Wellenfläche F C der gebrochenen Welle und der ebenen
Grenzfläche. Da die Strecke AF = c2 2τ als Kugelradius der von A ausgehenden Elementarwelle senkrecht auf der Einhüllenden F C steht, ergibt sich aus
dem rechtwinkligen Dreieck ACF
sin θ2 =
AF
c2 2τ
=
.
AC
AC
(7.6)
Aus den Gln. (7.3) und (7.6) folgt
sin θ1
c1
=
,
sin θ2
c2
(7.7)
141
7.3 Reflexion und Brechung
das SNELLIUSsche Brechungsgesetz. In der Optik wird üblicherweise statt der
Lichtgeschwindigkeit c der Brechungsindex n des betreffenden Mediums angegeben. Der Brechungsindex n ist definiert als der Quotient aus der Lichtgeschwindigkeit c0 im Vakuum und der Lichtgeschwindigkeit c in dem jeweiligen
Medium, in Zeichen
c0
.
(7.8)
n=
c
Mit Hilfe des Brechungsindex nimmt das SNELLIUSsche Brechungsgesetz die
in der Optik gebräuchliche Form
sin θ1
n2
=
sin θ2
n1
(7.9)
an, siehe Gl. (7.2). Wir haben damit gezeigt, daß sich sowohl das Reflexionsgesetz als auch das SNELLIUSsche Brechungsgesetz aus dem HUYGENSschen
Prinzip herleiten lassen. Im Rahmen dieser einfachen Herleitung können wir
allerdings keine Aussage darüber machen, wie sich die Intensität des einfallenden Strahls auf den reflektierten und den gebrochenen (transmittierten)
Strahl verteilt. Diese Frage läßt sich erst mit Hilfe einer elektromagnetischen
Lichttheorie beantworten.
Ein Material heißt optisch dichter als ein anderes, wenn sein Brechungsindex größer ist als derjenige des anderen Materials. Im anderen Fall heißt es
optisch dünner . In der nachfolgenden Tabelle sind die Brechungsindizes einiger
Stoffe angegeben für gelbes Natrium-Licht (Wellenlänge λ = 589 nm) bei der
Temperatur ϑ = 20 0 C und dem Druck p = 1, 01325 · 105 Pa.
Festkörper
n
Eis
Flußspat
Quarzglas
Kronglas BK 1
Flintglas F 3
Bariumoxid
Diamant
1,310
1,434
1,459
1,510
1,613
1,980
2,417
Flüssigkeiten
und Gase
Luft
Kohlendioxid
Wasser
Ethylalkohol
Benzol
Schwefelkohlenstoff
Methyleniodid
n
1,0003
1,0045
1,333
1,362
1,501
1,628
1,742
In der obigen Betrachtung (siehe Abb. 7.4) haben wir angenommen, daß ein
Lichtstrahl aus einem optisch dünneren auf ein optisch dichteres Medium trifft
(n1 < n2 ). In diesem Fall ergibt sich aus Gl. (7.9) θ2 < θ1 , d.h. der Lichtstrahl
wird zum Einfallslot hin gebrochen. Dasselbe gilt allgemein für Wellen, die aus
einem Medium mit größerer Ausbreitungsgeschwindigkeit auf ein Medium mit
kleinerer Ausbreitungsgeschwindigkeit treffen (c1 > c2 ).
142
7 Geometrische Optik
Trifft dagegen ein Lichtstrahl aus einem optisch dichteren Medium auf ein
optisch dünneres (n1 > n2 ), so folgt aus Gl. (7.9) θ2 > θ1 , d.h. der Lichtstrahl wird vom Einfallslot weg gebrochen. Dies gilt allgemein für Wellen,
die aus einem Medium mit kleinerer Ausbreitungsgeschwindigkeit auf ein Medium mit größerer Ausbreitungsgeschwindigkeit treffen (c1 < c2 ). Mit zunehmendem Einfallswinkel θ1 steigt der Brechungswinkel θ2 verstärkt an, bis bei
dem Einfallswinkel θ1 = θg der Brechungswinkel θ2 = 900 wird. Man nennt θg
den Grenzwinkel der Totalreflexion. Für θ1 > θg gibt es keinen gebrochenen
Strahl mehr, sondern nur noch den reflektierten Strahl. In Abb. 7.5 ist dies
dargestellt anhand von drei Strahlen, die von der punktförmigen Lichtquelle S
ausgehen. Für θ1 < θg geht ein Teil der Intensität des einfallenden Strahls in
Sr
1
θ1
n1
n2
S
S
2
θ1
-
θ1 *
3
2’
S
S
S
S
w 1’
S
Abbildung 7.5: Totalreflexion im Fall n1 > n2 . Strahl 1: θ1 < θg , Strahl 2:
θ1 = θg , Strahl 3: θ1 > θg
den reflektierten Strahl und der Rest in den gebrochenen Strahl, für θ1 > θg
geht die gesamte Intensität des einfallenden Strahls in den reflektierten Strahl.
Da bei dem Einfallswinkel θ1 = θg für den Brechungswinkel θ2 = 900 gilt, folgt
aus Gl. (7.9) für den Grenzwinkel der Totalreflexion θg
sin θg =
n2
.
n1
(7.10)
Ein Beispiel für die technische Anwendung der Totalreflexion ist die Übertragung von Daten mit Lichtwellenleitern (Glasfasern) in der optischen Nachrichtentechnik. Die Stufenindexfaser besteht aus einem Kern mit dem hohen
Brechungsindex nk , umgeben von einem Mantel mit dem niedrigeren Brechungsindex nm . Typische Abmessungen einer solchen Glasfaser sind: 50 µm
143
7.4 Brechung an sphärischen Grenzflächen
Kerndurchmesser, 125 µm Manteldurchmesser. Das an einem Ende der Glasfaser eingekoppelte Licht wird dann durch vielfache Totalreflexion zum anderen
Ende geleitet. Der Eintrittswinkel θ, unter dem ein Lichtstrahl auf die Stirnfläche der Faser trifft, darf allerdings nicht beliebig groß sein, weil sonst im
Innern der Faser die Totalreflexion nicht mehr gewährleistet ist (siehe Übungsaufgabe). Geordnete Bündel solcher Glasfasern leiten ein auf die Stirnfläche der
Fasern projiziertes Bild zum anderen Ende weiter. Die Ummantelung der einzelnen Fasern bewirkt hierbei, daß das Licht zweier sich berührender Fasern
nicht von der einen in die andere übertreten kann.
7.4
Brechung an sphärischen Grenzflächen
Als Vorbereitung für die Behandlung von Linsen wollen wir zunächst die Brechung an einer sphärischen Grenzfläche betrachten, die zwei Medien mit den
Brechnungsindizes n1 und n2 voneinander trennt, siehe Abb. 7.6. Im Abstand g
vor der sphärischen Grenzfläche befinde sich ein punktförmiger Gegenstand G.
Die Gerade durch G und den Mittelpunkt M der Kugelfläche wird als optische
Achse bezeichnet. Der Durchstoßpunkt der optischen Achse durch die Kugelfläche ist der Scheitelpunkt S. Wir betrachten einen beliebigen von dem Ge-
n1
θ1
A
β2
h
β1
n2
θ2
γ
r
G
S A
g
′
r
r
M
B
-
r
-
-
b
Abbildung 7.6: Brechung an einer sphärischen Grenzfläche
genstand G ausgehenden Lichtstrahl. Dieser treffe in dem Punkt A im Abstand
h von der optischen Achse auf die sphärische Grenzfläche. Wir setzen n2 > n1
144
7 Geometrische Optik
voraus, d.h. der einfallende Lichtstrahl wird zum Lot AM hin gebrochen. Hat
der Gegenstand G einen gewissen Mindestabstand von dem Scheitelpunkt S,
so schneidet der gebrochene Strahl die optische Achse in dem Punkt B, siehe
Abb. 7.6. Der Abstand b des Punktes B vom Scheitelpunkt S soll im folgenden
berechnet werden. Nach dem SNELLIUSschen Brechungsgesetz gilt
sin θ1
n2
=
.
sin θ2
n1
(7.11)
An dieser Stelle setzen wir voraus, daß der betrachtete Lichtstrahl nahe der
optischen Achse verläuft. Solche Strahlen werden auch als paraxial bezeichnet.
Das bedeutet, die Winkel β1 und β2 aber auch die Winkel θ1 , θ2 und γ können
als sehr klein angenommen werden. Mit der Näherung sin θ ≈ θ erhalten wir
aus Gl. (7.11)
n1 θ1 = n2 θ2 .
(7.12)
Da der Winkel θ1 Außenwinkel im Dreieck GM A und der Winkel γ Außenwinkel im Dreieck AM B ist, gilt
θ1 = β1 + γ
und
γ = θ2 + β2 .
Einsetzen dieser Beziehungen in Gl. (7.12) ergibt
n1 (β1 + γ) = n2 (γ − β2 ) .
(7.13)
Da die Winkel β1 , β2 und γ sehr klein sind, ist die Länge der Stecke SA′
vernachlässigbar gegenüber g, b und r. Somit gilt
β1 ≈ tan β1 ≈
h
,
g
β2 ≈ tan β2 ≈
h
,
b
γ ≈ tan γ ≈
h
.
r
Einsetzen dieser Beziehungen in Gl. (7.13) liefert
n1
h h
+
g
r
!
= n2
h h
−
r
b
!
.
Durch eine einfache Umformung erhält man
n1 n2
n2 − n1
+
=
.
g
b
r
(7.14)
Diese Gleichung zeigt, daß b unabhängig von h ist. Das bedeutet, alle paraxialen Strahlen, die von dem punktförmigen Gegenstand G ausgehen, werden an
der sphärischen Grenzfläche so gebrochen, daß sie sich in ein und demselben
7.4 Brechung an sphärischen Grenzflächen
145
Punkt B schneiden. Der Punkt B wird als das Bild des Gegenstandes G bezeichnet. Die Gegenstandsweite g und die Bildweite b sind durch die Gl. (7.14)
miteinander verbunden. Gl. (7.14) wird als Abbildungsgleichung für sphärische
Grenzflächen bezeichnet. Es sei noch einmal darauf hingewiesen, daß gemäß
unserer Herleitung ein scharfer Bildpunkt nur entsteht, wenn die Abbildung
durch paraxiale Strahlen erfolgt. Ist dies nicht der Fall, so entsteht eine Bildli”
nie“ auf der optischen Achse, da die weiter außen verlaufenden Strahlen stärker
gebrochen werden als die achsnahen Strahlen.
Liegt der Gegenstand im Unendlichen (g = ∞), so ergibt sich mit Gl. (7.14)
für die Bildweite b = fb
n2
n2 − n1
=
fb
r
bzw.
n2
r.
n2 − n1
Diese spezielle Bildweite fb wird bildseitige Brennweite und die zugehörige
Position Fb des Bildes bildseitiger Brennpunkt genannt. Fällt also ein Bündel
paralleler Lichtstrahlen auf eine sphärische Grenzfläche, so wird es in dem
bildseitigen Brennpunkt fokussiert.
Rückt der Gegenstand aus dem Unendlichen näher an die Grenzfläche heran,
so entfernt sich gemäß Gl. (7.14) der Bildpunkt immer weiter nach rechts.
Bei einer bestimmten Gegenstandsweite g = fg liegt das Bild schließlich im
Unendlichen (b = ∞). Aus Gl. (7.14) ergibt sich
fb =
n1
n2 − n1
=
fg
r
bzw.
n1
r.
n2 − n1
Diese spezielle Gegenstandsweite fg wird gegenstandseitige Brennweite und
die zugehörige Position Fg des Gegenstandes gegenstandseitiger Brennpunkt
genannt. Bringt man also eine punktförmige Lichtquelle in den gegenstandseitigen Brennpunkt, so breitet sich rechts von der sphärischen Grenzfläche ein
Bündel paralleler Lichtstrahlen aus.
Führt man den Gegenstand G auf der optischen Achse noch näher an den
Scheitelpunkt S heran, so reicht die Brechkraft des Mediums 2 nicht mehr aus,
um die einfallenden Lichtstrahlen zur optischen Achse hin zu brechen. Es kann
somit kein (reeller ) Bildpunkt mehr rechts vom Scheitelpunkt entstehen. Es
läßt sich aber zeigen (siehe Übungsaufgabe), daß alle von dem punktförmigen
Gegenstand G ausgehenden Lichtstrahlen an der sphärischen Grenzfläche so
fg =
146
7 Geometrische Optik
gebrochen werden, als kämen sie geradlinig von einem links von G auf der
optischen Achse liegenden Punkt B. Man spricht in diesem Fall von einem
virtuellen Bildpunkt. Die Bildweite b, also der Abstand des virtuellen Bildpunktes B vom Scheitelpunkt S, ist wieder durch Gl. (7.14) gegeben, wenn
man b negativ zählt, d.h. b < 0.
In Abb. 7.6 haben wir eine sphärische Grenzfläche betrachtet, deren Mittelpunkt M sich rechts vom Scheitelpunkt S befindet, also auf der dem einfallenden Licht abgewandten Seite. Liegt der Mittelpunkt M links vom Scheitelpunkt S, also auf derselben Seite wie das einfallende Licht, so kann man zeigen
(siehe Übungsaufgabe), daß Gl. (7.14) auch für die Brechung an einer solchen
Grenzfläche gültig bleibt. Man muß in diesem Fall allerdings den Radius r der
sphärischen Grenzfläche negativ nehmen, d.h. r < 0.
Nicht nur das Bild B, sondern auch der Gegenstand G kann virtuell sein.
Fällt ein Bündel konvergenter Lichtstrahlen von links so auf die sphärische
Grenzfläche, daß sie sich rechts vom Scheitelpunkt S in einem Punkt G schneiden würden, so spricht man von einem virtuellen punktförmigen Gegenstand.
Die Gegenstandsweite g, also der Abstand des Schnittpunktes G vom Scheitelpunkt S, ist in diesem Fall negativ zu nehmen, d.h. g < 0. Zusammenfassend
haben wir bei Gl. (7.14) folgende Vorzeichenkonvention zu berücksichtigen:
1. Die Gegenstandsweite g ist positiv, wenn sich der Gegenstand auf derselben Seite der Grenzfläche befindet wie das einfallende Licht. Andernfalls
ist die Gegenstandsweite negativ. Wenn g positiv ist, nennt man den Gegenstand reell , wenn g negativ ist, nennt man den Gegenstand virtuell .
2. Die Bildweite b ist positiv, wenn sich das Bild auf derselben Seite der
Grenzfläche befindet wie das austretende Licht. Andernfalls ist die Bildweite negativ. Wenn b positiv ist, nennt man das Bild reell , wenn b
negativ ist, nennt man das Bild virtuell .
3. Der Radius r der sphärischen Grenzfläche ist positiv, wenn sich der Mittelpunkt M auf derselben Seite der Grenzfläche befindet wie das austretende Licht. Andernfalls ist der Radius negativ.
7.5
Abbildung durch Linsen
Linsen sind transparente Körper, die von zwei gekrümmten Oberflächen begrenzt werden. Aus fertigungstechnischen Gründen sind die Oberflächen üblicherweise sphärisch. Linsen dienen in der Praxis zur Abbildung von Gegenständen. Die optische Achse einer sphärischen Linse ist die Gerade, die
147
7.5 Abbildung durch Linsen
durch die Mittelpunkte der beiden kugelförmigen Begrenzungsflächen geht.
Der Brechungsindex des Mediums, das die Linse umgibt, sei nm und der Brechungsindex des Linsenmaterials sei nl . Wir gehen von einem punktförmigen
Gegenstand aus, dessen Lichtstrahlen von links auf eine Linse treffen, siehe
Abb. 7.7. Die Strahlen werden dann zuerst an der linken und dann noch ein-
r
B′
r
G M2
S1
r2
g
S2
r
r
M1
B
r1
-
-
b
-
b′
-
d
Abbildung 7.7: Abbildung mit Hilfe einer dünnen sphärischen Linse
mal an der rechten sphärischen Grenzfläche gebrochen. Der Radius der linken
Grenzfläche sei r1 und der Radius der rechten sei r2 . Wir wollen annehmen, daß
die Abbildung nur mit Hilfe paraxialer Strahlen erfolgt, so daß wir Gl. (7.14)
benutzen können. Der Gegenstand G befinde sich in einem Abstand g von
dem Scheitelpunkt S1 der linken Grenzfläche. Bei der Brechung an der linken
Grenzfläche entsteht zunächst der virtuelle Bildpunkt B ′ , d.h. die von dem
Gegenstand G ausgehenden Lichtstrahlen werden an der linken Grenzfläche so
gebrochen, als kämen sie geradlinig von dem links von G auf der optischen
Achse liegenden Punkt B ′ . Für die Bildweite b′ dieses virtuellen Bildpunktes
gilt gemäß Gl. (7.14)
nm nl
nl − nm
+ ′ =
.
(7.15)
g
b
r1
Hierbei gilt b′ < 0, da es sich um einen virtuellen Bildpunkt handelt. Das von
der linken Grenzfläche erzeugte Bild wirkt als Gegenstand für die Brechung
an der rechten Grenzfläche. Bezüglich der rechten Grenzfläche hat der Punkt
B ′ die Gegenstandsweite g ′ = d + |b′ | = d − b′ . Hierbei bezeichnet d die Dicke
der Linse, also den Abstand der Scheitelpunkte S1 und S2 voneinander. Wir
148
7 Geometrische Optik
nehmen nun an, daß die Linse sehr dünn ist, d.h. d ist gegenüber allen anderen
räumlichen Abmessungen vernachlässigbar klein. Dann gilt in guter Näherung
g ′ = −b′ . Bei der Brechung an der rechten Grenzfläche entsteht der reelle Bildpunkt B. Das bedeutet, die scheinbar von dem Punkt B ′ kommenden Lichtstrahlen werden an der rechten Grenzfläche so gebrochen, daß sie sich in dem
rechts von S2 auf der optischen Achse liegenden Punkt B schneiden. Für die
Bildweite b dieses reellen Bildpunktes gilt gemäß Gl. (7.14)
nl
nm − nl
nm
=
+
.
′
−b
b
r2
(7.16)
Addition der Gleichungen (7.15) und (7.16) liefert
1
nm nm
1
+
= (nl − nm )
−
g
b
r1 r2
.
(7.17)
Dividiert man diese Gleichung durch nm und setzt n = nl /nm , womit n der
relative Brechungsindex der Linse in bezug auf ihre Umgebung ist, so erhält
man
1
1
1 1
,
(7.18)
+ = (n − 1)
−
g b
r1 r2
die Abbildungsgleichung für dünne sphärische Linsen. Häufig ist das die Linse
umgebende Medium Luft, so daß nm ≈ 1 und damit n ≈ nl gilt. Für dünne
Linsen (d ≈ 0) vereinigen sich die beiden Scheitelpunkte S1 und S2 , so daß die
Gegenstandsweite g und die Bildweite b statt von den Scheitelpunkten auch
von dem Linsenmittelpunkt aus gemessen werden kann.
Genau wie im Fall einer einzelnen sphärischen Grenzfläche wird die Bildweite zur bildseitigen Brennweite, wenn man den Gegenstand ins Unendliche legt
(g = ∞), und die gegenstandseitige Brennweite ergibt sich, wenn der Bildpunkt im Unendlichen liegt (b = ∞). Aus Gl. (7.18) folgt direkt, daß beide
Brennweiten identisch sind. Für die Brennweite f einer dünnen sphärischen
Linse gilt
1
1
1
.
(7.19)
= (n − 1)
−
f
r1 r2
Diese Gleichung wird Linsenschleiferformel genannt. Mit Hilfe von Gl. (7.19)
läßt sich die Abbildungsgleichung, Gl. (7.18), auch in der Form
1
1 1
+ =
g b
f
(7.20)
schreiben. Da wir bei der Herleitung von Gl. (7.20) zweimal von Gl. (7.14)
für die Brechung an einer sphärischen Grenzfläche Gebrauch gemacht haben,
149
7.5 Abbildung durch Linsen
bleibt für die Abbildung durch eine Linse die im vorigen Abschnitt dargestellte
Vorzeichenkonvention gültig. Die Größe D := 1/f wird als Brechkraft einer
Linse bezeichnet. Die Einheit der Brechkraft wird Dioptrie genannt und hat
das Kurzzeichen dpt, d.h. es gilt [D] = m−1 = dpt.
Der Raum vor der Linse, in dem sich das einfallende Licht ausbreitet, wird
als Gegenstandsraum, der Raum hinter der Linse, in dem sich das austretende Licht ausbreitet, als Bildraum bezeichnet. Nicht nur für die in Abb. 7.7
dargestellte bikonvexe Linse, sondern für alle sphärischen Linsen läßt sich mit
Gl. (7.19) die Brennweite berechnen, siehe Abb. 7.8. Man hat lediglich die Vorzeichenkonvention für die Krümmungsradien der sphärischen Grenzflächen zu
berücksichtigen; der Radius ist positiv zu nehmen, wenn sich der Mittelpunkt
M der Grenzfläche auf derselben Seite befindet wie das austretende Licht,
also im Bildraum. Andernfalls ist der Radius negativ zu nehmen. Die ersten
bikonvex
plankonvex
konkavkonvex
bikonkav
plankonkav
konvexkonkav
r1 > 0
r2 < 0
r1 = ∞
r2 < 0
r1 < r2 < 0
r1 < 0
r2 > 0
r1 = ∞
r2 > 0
r2 < r1 < 0
f >0
f >0
f >0
f <0
f <0
f <0
Abbildung 7.8: Linsenformen
drei Linsentypen haben eine positive Brennweite und werden Sammellinsen genannt. Die positive Brennweite zeigt an, daß sowohl der bildseitige als auch der
gegenstandseitige Brennpunkt reell ist. Fällt ein Bündel paralleler Lichtstrahlen parallel zur optischen Achse auf eine Sammellinse, so werden die Strahlen
hinter der Linse im bildseitigen Brennpunkt Fb fokussiert (gesammelt). Diese
Eigenschaft gibt den Sammellinsen ihren Namen. In Abb. 7.9a ist dies für eine
bikonvexe Linse dargestellt. Umgekehrt werden alle Strahlen, die durch den ge-
150
7 Geometrische Optik
genstandseitigen Brennpunkt Fg gehen, von einer Sammellinse so gebrochen,
daß sie hinter der Linse parallel zur optischen Achse verlaufen. Die letzten
drei Linsentypen haben eine negative Brennweite und werden Zerstreuungslinsen genannt. Die negative Brennweite zeigt an, daß sowohl der bildseitige
als auch der gegenstandseitige Brennpunkt virtuell ist. Fällt ein Bündel paralleler Lichtstrahlen parallel zur optischen Achse auf eine Zerstreuungslinse,
so werden die Strahlen von der Linse so gebrochen, als kämen sie von dem im
Gegenstandsraum liegenden virtuellen Brennpunkt Fb . In Abb. 7.9b ist dies für
eine bikonkave Linse dargestellt. Umgekehrt werden alle Strahlen, die auf den
im Bildraum liegenden virtuellen Brennpunkt Fg zulaufen, von einer Zerstreuungslinse so gebrochen, daß sie hinter der Linse parallel zur optischen Achse
verlaufen. Nur mit Sammellinsen lassen sich reelle Bilder erzeugen, wohingegen
Zerstreuungslinsen lediglich virtuelle Bilder liefern.
(a)
-
Fb
-
Fg
*
(b)
Fb
:
XX X
H
HH
XXz
X
Fg
-
HH
j
H
Abbildung 7.9: Die reellen Brennpunkte einer Sammellinse (a) und die virtuellen Brennpunkte einer Zerstreunugslinse (b)
Eine Linse bildet nun nicht nur Gegenstandspunkte, die auf der optischen
Achse liegen, sondern auch Gegenstandspunkte, die in der Nähe der optischen Achse liegen, auf entsprechende Bildpunkte ab. Auf diese Weise können
mit einer Linse auch ausgedehnte Gegenstände abgebildet werden. Die Ebene
senkrecht zur optische Achse, in der sich der Gegenstand befindet, wird als
151
7.5 Abbildung durch Linsen
Gegenstandsebene und die Ebene, in der sich das Bild befindet als Bildebene bezeichnet. Der Abstand der Gegenstandsebene von der Linsenmitte (die
Gegenstandsweite g) und der Abstand der Bildebene von der Linsenmitte (die
Bildweite b) sind durch die Abbildungsgleichung (7.20) miteinander verknüpft.
Das Bild, das durch eine dünne Linse von einem ausgedehnten Gegenstand
erzeugt wird, kann mit Hilfe von drei ausgezeichneten Strahlen konstruiert
werden. Bereits zwei dieser drei Strahlen legen durch ihren Schnittpunkt das
Bild fest. Ihr Verlauf ist im folgenden beschrieben, siehe auch Abb. 7.10.
Der Strahl 1 verläuft im Gegenstandsraum parallel zur optischen Achse
und wird dann so gebrochen, daß er durch den bildseitigen Brennpunkt Fb
geht. Da wir dünne Linsen vorausgesetzt haben, begeht man praktisch keinen
Fehler, wenn man den Strahl parallel zur optischen Achse bis zur Mittelebene
der Linse durchzieht und dann geradlinig durch den Brennpunkt Fb verlaufen
läßt.
Der Strahl 2 (Hauptstrahl) geht durch den Mittelpunkt O der Linse.
Bei dünnen Linsen erfährt dieser Strahl näherungsweise keine Brechung und
verläuft somit geradlinig durch den Linsenmittelpunkt.
Der Strahl 3 geht durch den gegenstandseitigen Brennpunkt Fg und
verläuft im Bildraum parallel zur optischen Achse. Auch dieser Strahl wird
bis zur Mittelebene der dünnen Linse durchgezogen und dann parallel zur optischen Achse weitergeführt.
1
2
G′
6
Fb
r
G
B
r
Fg
O
3
?
B′
g
-
-
b
Abbildung 7.10: Geometrische Konstruktion des von einer dünnen Sammellinse
erzeugten reellen Bildes
Durch diese drei Strahlen wird nicht nur der Ort, sondern auch die Größe
und die Orientierung (aufrecht oder umgekehrt) des Bildes festgelegt. Die
152
7 Geometrische Optik
Gegenstandsgröße ist durch GG′ und die Bildgröße durch BB ′ gegeben. In
Ergänzung zu unserer weiter oben getroffenen Vorzeichenkonvention setzen
wir hier noch fest, daß Strecken, die senkrecht zur optischen Achse verlaufen,
oberhalb der optischen Achse positiv und unterhalb der optischen Achse negativ gezählt werden. Für die in Abb. 7.10 dargestellte Situation gilt GG′ > 0
und BB ′ < 0. Das Verhältnis der Bildgröße zur Gegenstandsgröße wird als der
Abbildungsmaßstab β definiert, in Zeichen
β=
BB ′
.
GG′
Der Abbildungsmaßstab ist demnach positiv, wenn das Bild dieselbe Orientierung hat wie der Gegenstand, und negativ, wenn ein umgekehrtes Bild entsteht.
Da die Dreiecke GOG′ und BOB ′ ähnlich sind, gilt |BB ′ |/GG′ = b/g. Damit
ergibt sich
b
β=− .
(7.21)
g
Ist |β| > 1, so ist das Bild vergrößert, ist |β| < 1, so ist das Bild verkleinert.
Liegt die Gegenstandsweite g zwischen ∞ und 2f , so liegt die Bildweite b
zwischen f und 2f . Aus Gl. (7.21) folgt, daß die Sammellinse in diesem Fall ein
verkleinertes, umgekehrtes Bild liefert. Liegt die Gegenstandsweite g zwischen
2f und f , so liegt die Bildweite b zwischen 2f und ∞. Aus Gl. (7.21) folgt,
daß die Sammellinse nun ein vergrößertes, umgekehrtes Bild liefert. In beiden
Fällen kann man die Bilder auf einem Schirm sichtbar machen. Solche Bilder
heißen reelle Bilder .
Ist die Gegenstandsweite g kleiner als die Brennweite f , so ergibt sich aus
der Abbildungsgleichung (7.20) eine negative Bildweite b. Das bedeutet, daß
in diesem Fall ein virtuelles Bild entsteht. Auch dieses kann mit Hilfe der oben
beschriebenen Strahlen konstruiert werden, siehe Abb. 7.11. Die Strahlen 1 und
2 schneiden sich allerdings nicht mehr im Bildraum, sondern ihre rückwärtigen
Verlängerungen schneiden sich im Gegenstandsraum. Dort entsteht das virtuelle Bild. Auch der Strahl 3 (in Abb. 7.11 nicht eingezeichnet) kann verwendet
werden. Er ist als Strahl anzusetzen, der von G′ ausgeht und von Fg herzukommen scheint. Verlängert man den entsprechenden gebrochenen Strahl, der
im Bildraum parallel zur optischen Achse verläuft, rückwärts, so schneidet er
sich mit den rückwärtigen Verlängerungen der beiden anderen Strahlen in B ′ .
Die Bedeutung des virtuellen Bildes soll noch einmal deutlich hervorgehoben
werden. Alle von einem Gegenstandspunkt, z.B. G′ , ausgehenden Lichtstrahlen
werden von der Linse so gebrochen, als kämen sie von dem ebenfalls im Gegenstandsraum liegenden Punkt B ′ . Ein Beobachter im Bildraum nimmt das
von G′ ausgehende Licht also so wahr, als käme es von B ′ . Entsprechendes gilt
153
7.5 Abbildung durch Linsen
B′
6
G′ 6
r
B
r
Fg G
O
g
Fb
1
2
-
b
Abbildung 7.11: Geometrische Konstruktion des von einer dünnen Sammellinse
erzeugten virtuellen Bildes
natürlich auch für alle anderen Gegenstandspunkte. Man kann ein virtuelles
Bild demnach mit dem Auge wahrnehmen oder photographieren, nicht aber
auf einem Schirm sichtbar machen.
Zusammenfassend ergeben sich für den Ort, die Größe und die Orientierung
des von einer Sammellinse erzeugten Bildes in Abhängigkeit von der Gegenstandsweite g die in der folgenden Tabelle aufgeführten Werte:
g
∞ . . . 2f
2f . . . f
f . . . +0
b
f . . . 2f
2f . . . ∞
−∞ . . . −0
β
β < 0 , |β| ≤ 1
β < 0 , |β| ≥ 1
β>1
Art des Bildes
reell
reell
virtuell
Aus der Abbildungsgleichung (7.20) folgt, daß Zerstreuungslinsen auf Grund
ihrer negativen Brennweite nur virtuelle Bilder erzeugen können. Diese Bilder
können ebenfalls mit Hilfe der drei ausgezeichneten Strahlen konstruiert werden. Man muß lediglich berücksichtigen, daß bei einer Zerstreuungslinse die
beiden Brennpunkte Fg und Fb virtuell sind. Die drei Strahlen haben dann
folgenden Verlauf, siehe auch Abb. 7.12.
Der Strahl 1 verläuft im Gegenstandsraum parallel zur optischen Achse
und wird dann so gebrochen, als käme er von dem im Gegenstandsraum liegenden virtuellen Brennpunkt Fb . Da wir dünne Linsen vorausgesetzt haben,
kann man den Strahl parallel zur optischen Achse bis zur Mittelebene der
154
7 Geometrische Optik
Linse durchziehen und dann geradlinig so weiterführen, daß seine rückwärtige
Verlängerung durch den Brennpunkt Fb geht.
Der Strahl 2 (Hauptstrahl) geht durch den Mittelpunkt O der Linse.
Bei dünnen Linsen erfährt dieser Strahl näherungsweise keine Brechung und
verläuft somit geradlinig durch den Linsenmittelpunkt.
Der Strahl 3 läuft im Gegenstandsraum geradlinig auf den im Bildraum
liegenden virtuellen Brennpunkt Fg zu und wird dann so gebrochen, daß er im
Bildraum parallel zur optischen Achse verläuft. Auch dieser Strahl wird bis zur
Mittelebene der dünnen Linse durchgezogen und dann parallel zur optischen
Achse weitergeführt.
Der Schittpunkt des Strahls 2 mit den rückwärtigen Verlängerungen der
Strahlen 1 und 3 liefert dann die Spitze B ′ des virtuellen Bildes.
G′
HH
6
G
HH B ′
HH
6HH
r
H
Fb B
>
1
- 3
H
r
HH
Fg
HH
H
Hj
H
2
-
b
g
-
Abbildung 7.12: Geometrische Konstruktion des von einer dünnen Zerstreuungslinse erzeugten virtuellen Bildes
Bei den obigen Betrachtungen haben wir stets vorausgesetzt, daß die Abbildung ausschließlich durch paraxiale Strahlen erfolgt. Ist dies nicht der Fall,
so treten verschiedene Abbildungsfehler auf. Erfolgt die Abbildung mit Licht
verschiedener Wellenlänge (z.B. weißem Licht), so ergibt sich ein weiterer Abbildungsfehler, der daher kommt, daß der Brechungsindex n und damit auch
die Bildweite b von der Wellenlänge λ abhängen. Durch den Einsatz von Linsensystemen lassen sich diese Abbildungsfehler weitgehend korrigieren.
7.6. DAS MENSCHLICHE AUGE
7.6
155
Das menschliche Auge
Viele optische Instrumente dienen als Sehhilfe für das Auge. Da das Auge selbst
wesentlicher Bestandteil des Sehvorgangs ist, wollen wir uns zunächst mit diesem befassen. In Abb. 7.13 ist der Aufbau des menschlichen Auges schematisch
dargestellt. Die lichtdurchlässigen Teile des Auges sind die Hornhaut H, die
mit Kammerwasser gefüllte vordere und hintere Augenkammer K, die Linse Li
sowie der Glaskörper G. Die von Muskelfasern durchzogene, lichtundurchlässige Iris I regelt über ihre kreisrunde Öffnung (Pupille) die Lichtmenge, die in
das Auge fällt. Seine Form erhält das Auge durch die stabile Lederhaut Le.
Abbildung 7.13: Querschnitt durch das menschliche Auge
Auf dieser befindet sich innen die Aderhaut A, die mit ihren Blutgefäßen zur
Versorgung der unmittelbar auf ihr liegenden, hauchdünnen Netzhaut N dient.
In der Netzhaut N befinden sich die lichtempfindlichen Sinneszellen (Photorezeptoren), die Stäbchen und die Zäpfchen. Die extrem lichtempfindlichen
Stäbchen dienen der Wahrnehmung bei geringer Helligkeit, vermitteln aber
nur Helligkeitsstufen. Die weniger empfindlichen Zäpfchen dienen dagegen der
Wahrnehmung bei stärkerer Beleuchtung und vermitteln den Farbeindruck.
In der Mitte der Netzhaut gegenüber der Linse befindet sich die Netzhautgrube NG, auch gelber Fleck genannt. Nur Bilder, die auf die Netzhautgrube fallen,
können scharf gesehen werden. Sie nimmt eine Fläche von wenigen Quadratmillimetern ein und enthält ausschließlich Zäpfchen in großer Dichte. Beim
Betrachten größerer Gegenstände tastet das Auge den Gegenstand ab, und
durch Verrechnung im Gehirn werden die scharfen Teilbilder zu einem scharfen
Gesamtbild zusammengesetzt. Im blinden Fleck B, wo die ableitenden Nervenfasern der Netzhaut in den Sehnerv eintreten, fehlen Sehzellen. Dort können
keine optischen Reize aufgenommen werden.
156
7 Geometrische Optik
Da die Bildweite beim Auge durch den Abstand zwischen Linse und Netzhaut festliegt, muß die Brechkraft der Augenlinse variierbar sein, damit Gegenstände in unterschiedlicher Entfernung scharf gesehen werden können. Dies
wird durch den Ziliarmuskel Z erreicht, der die Krümmung der Linse und
damit ihre Brechkraft verändert. Diese Entfernungsanpassung heißt Akkommodation. Das normalsichtige Auge ist bei entspanntem Ziliarmuskel so eingestellt, daß unendlich ferne Gegenstände scharf gesehen werden. In diesem
Fall hat die Linse ihre maximale Brennweite, und ihr bildseitiger Brennpunkt
liegt auf der Netzhaut. Werden näher gelegene Gegenstände betrachtet, so kontrahiert der Ziliarmuskel und der Zug auf die Linse läßt nach. Dadurch wird
die Krümmung der Linse vergrößert und die Brennweite verkleinert. Der dem
Auge am nächsten gelegene Punkt, der bei stärkster Akkommodation gerade
noch scharf gesehen werden kann, wird Nahpunkt genannt. Sein Abstand vom
Auge beträgt beim Jugendlichen etwa 100 mm und nimmt mit dem Alter wegen der geringer werdenden Akkommodationsfähigkeit zu. Als Bezugssehweite
oder deutliche Sehweite wurde der Abstand s0 = 250 mm festgelegt. Das ist
die kürzeste Enfernung, bei der ein normalsichtiger erwachsener Mensch einen
Gegenstand längere Zeit ohne besondere Anstrengung betrachten kann.
Zwei Punkte werden nur dann vom Auge getrennt wahrgenommen, wenn
ihre Bilder auf verschiedene Zäpfchen fallen. Da die Dichte der Zäpfchen in
der Netzhautgrube am größten ist, ist dort auch das Auflösungsvermögen des
Auges am größten. Der physiologische Grenzwinkel , unter dem Gegenstände
noch getrennt wahrgenommen werden, beträgt etwa eine Bogenminute. In der
Bezugssehweite s0 entspricht diesem Winkel ein Abstand von 0, 07 mm.
Der Punkt, der mit entspanntem Auge scharf gesehen werden kann, wird
Fernpunkt genannt. Beim normalsichtigen Auge liegt er im Unendlichen. Beim
kurzsichtigen Auge ist der Augapfel zu lang, so daß parallel einfallende Strahlen
schon vor der Netzhaut fokussiert werden. Bei entspanntem Auge liegt beim
Kurzsichtigen der bildseitige Brennpunkt also vor der Netzhaut. Der Kurzsichtige kann deshalb weit entfernte Gegenstände ohne Sehhilfe nicht scharf
sehen, sein Fernpunkt liegt im Endlichen. Zur Abhilfe wird eine Brille mit
Zerstreuungslinsen verwendet.
Beim angeboren weitsichtigen Auge ist der Augapfel zu kurz, so daß parallel
einfallende Strahlen erst hinter der Netzhaut fokussiert werden. Bei entspanntem Auge liegt beim Weitsichtigen der bildseitige Brennpunkt also hinter der
Netzhaut. Der Weitsichtige kann zwar durch Akkommodation weit entfernte
Gegenstände scharf sehen, die ständige Anspannung des Ziliarmuskels wirkt
aber ermüdend, und Gegenstände in geringer Entfernung können überhaupt
nicht scharf gesehen werden. Zur Abhilfe wird eine Brille mit Sammellinsen
verwendet.
157
7.7. OPTISCHE INSTRUMENTE
7.7
7.7.1
Optische Instrumente
Vergrößerung durch optische Instrumente
Wenn man einen kleinen Gegenstand genauer betrachten will, führt man ihn
näher an das Auge heran. Man vergrößert auf diese Weise den Sehwinkel , unter
dem man den Gegenstand wahrnimmt. Unter dem Sehwinkel ε versteht man
den Winkel, welchen die beiden Grenzstrahlen vom Gegenstand zum Auge bilden, siehe Abb. 7.14. Alle Gegenstände mit gleich großem Sehwinkel werden
y6
ε
Abbildung 7.14: Zur Definition des Sehwinkels ε
vom Auge als gleich groß wahrgenommen, da sie auf der Netzhaut gleich große
Bilder ergeben. Weil das Auge nur bis zum Nahpunkt akkommodieren kann,
erhält man das größte scharfe Bild, wenn sich der Gegenstand im Nahpunkt
befindet. Eine weitere Vergrößerung des Sehwinkels ist nur möglich, wenn optische Instrumente zur Hilfe genommen werden. Da das Netzhautbild dem
Tangens des Sehwinkels proportional ist, definiert man als Vergrößerung eines
optischen Instruments
tan ε
.
(7.22)
Γ=
tan ε0
Dabei ist ε der Sehwinkel mit und ε0 der Sehwinkel ohne Zuhilfenahme des
optischen Instruments. Die Winkel ε und ε0 sind im allgemeinen sehr klein, so
daß gemäß Gl. (7.22) in guter Näherung Γ ≈ ε/ε0 gilt. Weil die Akkommodation des normalsichtigen Auges auf kleinere Entfernungen als s0 = 250 mm als
anstrengend empfunden wird, wird der Sehwinkel ε0 für Gegenstände, die sich
aus der Nähe betrachten lassen, auf die deutliche Sehweite s0 bezogen. Ist y
die Gegenstandsgröße, so erhält man für den Sehwinkel ε0
tan ε0 =
y
.
s0
(7.23)
158
7.7.2
7 Geometrische Optik
Lupe
Die Lupe ist eine Sammellinse kurzer Brennweite und dient dazu, von dem Gegenstand ein virtuelles, vergrößertes, aufrechtes Bild zu erzeugen. Dazu muß
sich der Gegenstand innerhalb der einfachen Brennweite befinden. Um das Bild
mit entspanntem Auge betrachten zu können, muß das Bild im Unendlichen
liegen. Der Gegenstand ist deshalb in die gegenstandseitige Brennebene zu
bringen, siehe Abb. 7.15. Die unter diesen Bedingungen auftretende Vergrößerung wird als Standardvergrößerung der Lupe bezeichnet. Aus Abb. 7.15 liest
y
6
ε
ε
F
-
f
Abbildung 7.15: Strahlengang bei der Lupe
man für den Sehwinkel, unter dem das virtuelle Bild im Unendlichen gesehen
wird, die Beziehung
y
tan ε =
f
ab, wobei f die Brennweite der Linse ist. Setzt man dies in Gl. (7.22) ein, so
erhält man mit Gl. (7.23) für die Standardvergrößerung der Lupe
Γ=
s0
.
f
(7.24)
Die Standardvergrößerung einer Lupe ist also um so größer, je kleiner ihre
Brennweite f ist. Kleine Brennweiten bedingen kleine Krümmungsradien der
sphärischen Grenzflächen. Da sich mit zunehmender Krümmung der Grenzflächen Abbildungsfehler immer stärker bemerkbar machen, läßt sich mit Lupen maximal eine 25-fache Standardvergrößerung erreichen.
159
7.7 Optische Instrumente
7.7.3
Mikroskop
Für stärkere Vergrößerungen muß man ein Mikroskop zu Hilfe nehmen. Es
besteht im einfachsten Fall aus zwei Sammellinsen, dem Objektiv und dem
Okular . Das Objektiv Ob entwirft von dem Gegenstand der Größe y ein vergrößertes, umgekehrtes, reelles Zwischenbild der Größe y ′ . Dieses Zwischenbild
wird mit Hilfe des Okulars Ok betrachtet. Das Okular wirkt dabei wie eine
Lupe, d.h. es erzeugt von dem reellen Zwischenbild ein vergrößertes virtuelles
Bild. Um Ermüdungen des Auges zu vermeiden, bringt man den Gegenstand
so nah an das Objektiv heran, daß das reelle Zwischenbild in der gegenstandseitigen Brennebene des Okulars entsteht, wodurch das vom Okular erzeugte
virtuelle Bild dann im Unendlichen liegt. Der Strahlengang in einem Mikroskops ist in Abb. 7.16 dargestellt. Für den Sehwinkel ε, unter dem das virtuelle
Okular
Objektiv
F1 ′
y 6
F2
F1
F2 ′
ε
y′
?
-
fOb
-
fOb
-
t
-
fOk
-
fOk
Abbildung 7.16: Strahlengang beim Mikroskop
Bild im Unendlichen gesehen wird, liest man aus Abb. 7.16 die Beziehung
tan ε =
y′
fOk
(7.25)
ab, wobei fOk die Brennweite des Okulars ist. Hierbei ist zu beachten, daß y ′
und ε negativ sind, da y ′ eine Strecke und ε einen Winkel unterhalb der optischen Achse bezeichnet. Der Abstand der Brennpunkte F1′ und F2 voneinander
wird als optische Tubuslänge t bezeichnet und ist zu t = 160 mm normiert worden. Mit Hilfe der optischen Tubuslänge t, der Gegenstandsgröße y und der
Brennweite fOb kann man y ′ aus Gl. (7.25) eliminieren. Aus Abb. 7.16 ergibt
sich die Beziehung y ′ /y = −t/fOb , bzw. y ′ = −(t/fOb )y. Setzt man dies in
Gl. (7.25) ein, so folgt
ty
tan ε = −
.
(7.26)
fOb fOk
160
7 Geometrische Optik
Wird der Sehwinkel ε0 ohne Zuhilfenahme des optischen Instruments wieder
auf die deutliche Sehweite s0 bezogen, so erhält man mit den Gln. (7.22) und
(7.23) für die Standardvergrößerung des Mikroskops
Γ=−
t s0
.
fOb fOk
(7.27)
Das Minuszeichen in dieser Beziehung deutet an, daß das betrachtete Bild
umgekehrt ist. Da s0 und t festliegen, wird Γ um so größer, je kleiner die
Brennweiten von Objektiv und Okular sind. Mit dem Abbildungsmaßstab des
Objektivs
y′
t
βOb =
=−
y
fOb
und der Standardvergrößerung des als Lupe wirkenden Okulars
ΓOk =
s0
fOk
läßt sich die Standardvergrößerung des Mikroskops auch in folgender Form
schreiben
Γ = βOb ΓOk .
(7.28)
Mit den handelsüblichen Objektiven lassen sich Abbildungsmaßstäbe |βOb | zwischen 8 und 100, mit den Okularen Vergrößerungen bis zu ΓOk = 25 erreichen,
so daß die besten Mikroskope Standardvergrößerungen bis |Γ| = 2500 erzielen.
7.7.4
Fernrohr
Ein Fernrohr hat die Aufgabe, den Sehwinkel weit entfernter Gegenstände zu
vergrößern. Das KEPLERsche Fernrohr besteht aus zwei Sammellinsen. Mit
Hilfe der ersten Sammellinse, dem Objektiv, wird von dem weit entfernten Gegenstand in der bildseitigen Brennebene ein verkleinertes, umgekehrtes, reelles
Bild erzeugt. Dieses Zwischenbild der Größe y ′ wird mit der als Lupe wirkenden zweiten Sammellinse, dem Okular, betrachtet. Das vom Okular entworfene
virtuelle Bild sollte wieder im Unendlichen liegen, so daß es mit entspanntem
Auge wahrgenommen werden kann. Zu diesem Zweck müssen der bildseitige
Brennpunkt F1′ des Objektivs und der gegenstandseitige Brennpunkt F2 des
Okulars zusammenfallen. Der Strahlengang in einem KEPLERschen Fernrohr
ist in Abb. 7.17 dargestellt. Da das Fernrohr zur Beobachtung weit entfernter Gegenstände eingesetzt wird, muß in der Beziehung für die Vergrößerung,
Gl. (7.22), für ε0 der Sehwinkel eingesetzt werden, unter dem man den Gegenstand mit bloßem Auge wahrnimmt. Aus Abb. 7.17 liest man für ε0 die
161
7.7 Optische Instrumente
Objektiv
Okular
F1 ′ = F2
ε0
F2 ′
ε
y′
F1
?
-
fOb
-
fOb
-
fOk
-
fOk
Abbildung 7.17: Strahlengang beim KEPLERschen Fernrohr
Beziehung
tan ε0 = −
y′
fOb
(7.29)
ab, wobei fOb die Brennweite des Objektivs ist. Hierbei ist wieder zu beachten,
daß y ′ negativ ist. Für den Sehwinkel ε, unter dem das vom Okular entworfene
virtuelle Bild im Unendlichen gesehen wird, entnimmt man aus Abb. 7.17 die
Beziehung
y′
tan ε =
,
(7.30)
fOk
wobei fOk die Brennweite des Okulars ist. Mit den Gln. (7.29) und (7.30) folgt
für die Vergrößerung des Fernrohrs
Γ=−
fOb
.
fOk
(7.31)
Ein Fernrohr vergrößert demnach um so stärker, je größer die Brennweite des
Objektivs und je kleiner die Brennweite des Okulars ist. Das Minuszeichen
zeigt an, daß das betrachtete Bild umgekehrt ist.
162
7 Geometrische Optik
Kapitel 8
Beugung
8.1
FRAUNHOFERsche und FRESNELsche
Beugung
In einem homogenen, unendlich ausgedehnten Medium breiten sich die Schwingungszustände einer Welle überall geradlinig aus, und zwar längs der Wellennormalen, die auch als Strahlen bezeichnet werden. Sind die Wellen jedoch
räumlich begrenzt, was z.B. durch die endlichen Abmessungen des Senders
oder durch Hindernisse im welleleitenden Medium verursacht werden kann,
so tritt eine Abweichung von der geradlinigen Wellenausbreitung auf. Dieses
Phänomen wird Beugung genannt und läßt sich mit Hilfe des HUYGENSschen
Prinzips erklären. Trifft beispielsweise eine ebene Welle auf eine spaltförmige Öffnung, so kann nach dem HUYGENSschen Prinzip jeder Punkt in dem
Spalt als Ausgangspunkt von kugelförmigen Elementarwellen angesehen werden. Damit müssen auch Wellen in den geometrischen Schattenraum“ ge”
langen. In jedem Punkt hinter der Öffnung ergibt sich die Amplitude der dort
eintreffenden Welle durch die Überlagerung aller von der Öffnung ausgehenden
Elementarwellen. Dabei kann es an bestimmten Stellen zu einer Verstärkung
der einzelnen Elementarwellen kommen, an anderen Stellen jedoch zu einer
vollständigen Auslöschung. Dies läßt sich am einfachsten bei Oberflächenwellen in einer mit Wasser gefüllten Schale demonstrieren. Daß die Beugung von
Licht in unserer Umwelt von uns kaum wahrgenommen wird, liegt daran, daß
sich die Beugungserscheinungen um so stärker bemerkbar machen, je weniger
sich die linearen Abmessungen des beugenden Objekts von der Wellenlänge
unterscheiden. Obwohl wir im folgenden meist von Licht sprechen, soll hier
noch einmal betont werden, daß das Phänomen der Beugung bei allen Wellen
auftritt, egal ob es sich um Licht-, Schall- oder Oberflächenwellen handelt.
163
164
8 Beugung
Bei der Untersuchung von Beugungserscheinungen unterscheidet man zwei
Fälle der experimentellen Ausführung. Bei der FRESNELschen Beugung
(A. J. FRESNEL, 1788 - 1827) liegen die Lichtquelle L und der Beobachtungspunkt P auf dem Schirm in einem endlichen Abstand vor bzw. hinter der
beugenden Öffnung, siehe Abb. 8.1a. Liegt sowohl die Lichtquelle als auch der
Beobachtungsschirm im Unendlichen, so spricht man von FRAUNHOFERscher Beugung (J. FRAUNHOFER, 1787 - 1826), siehe Abb. 8.1b. Auf das
Beugungsobjekt fällt dann ein Bündel paralleler Lichtstrahlen, und die Lichtstrahlen, die von dem Beugungsobjekt zu dem Beobachtungspunkt gelangen,
sind ebenfalls parallel. Experimentell kann man die FRAUNHOFERsche BeuPr
(a)
Lr
(b)
-
*
*
*
*
Pr
(c)
Lr
-
f
-
f
Abbildung 8.1: Beugung an einer Öffnung. FRESNELsche Beugung (a),
FRAUNHOFERsche Beugung (b), experimentelle Realisierung der FRAUNHOFERschen Beugung (c)
gung dadurch realisieren, daß man die Lichtquelle in den vorderen Brennpunkt
einer vor dem beugenden Objekt stehenden Linse und den Schirm in den hinteren Brennpunkt einer hinter dem beugenden Objekt stehenden Linse stellt,
165
8.2 Beugung am Spalt
siehe Abb. 8.1c. Die mathematische Beschreibung der FRAUNHOFERschen
Beugung ist bedeutend einfacher als die der FRESNELschen, weshalb wir uns
im folgenden ausschließlich mit der ersteren befassen wollen.
8.2
Beugung am Spalt
In diesem Abschnitt wollen wir das Beugungsmuster berechnen, welches sich
ergibt, wenn Licht durch einen schmalen Spalt tritt. Wir betrachten FRAUNHOFERsche Beugung, d.h. der Schirm, auf dem das durch den Spalt tretende
Licht aufgefangen wird, möge sich in einem Abstand l vom Spalt befinden, der
sehr groß ist verglichen mit der Spaltbreite b. Der Spalt werde mit linear polarisiertem Licht der Wellenlänge λ beleuchtet. Um die Intensitätsverteilung
des auf den Schirm treffenden Lichtes zu berechnen, teilen wir den Spalt in
unendlich viele elementare Spalte der infinitesimalen Breite dy. Wir addieren
dann für einen beliebigen Punkt des Schirms die elektrischen Feldstärken, die
von den einzelnen elementaren Spalten herrühren, und bekommen so die gesamte elektrische Feldstärke in dem Punkt. Die mittlere Intensität erhalten
wir schließlich durch Quadrieren der Amplitude der elektrischen Feldstärke.
−b/2
θ
0
y
dy
b/2
θ
?
1
1
l
y sin θ
Abbildung 8.2: FRAUNHOFERsche Beugung an einem Spalt. Um einen Ausdruck für die Intensitätsverteilung des gebeugten Lichtes herzuleiten, wird der
Spalt in unendlich viele elementare Spalte der infinitesimalen Breite dy unterteilt.
In Abb. 8.2 ist ein Spalt mit der Unterteilung in die elementaren Spalte dargestellt. Die Koordinate y, die die Position der elementaren Spalte beschreibt,
166
8 Beugung
wird von der Spaltmitte aus gemessen. In der Richtung senkrecht zur Zeichenebene sei der Spalt sehr weit ausgedehnt verglichen mit der Spaltbreite b.
Wegen der linienhaften Form der elementaren Spalte kann man die von diesen
ausgehenden Elementarwellen als Zylinderwellen ansehen. Die Überlagerung
dieser Zylinderwellen in den verschieden Richtungen soll im folgenden berechnet werden. Die Richtungen werden angegeben durch den Winkel θ gegenüber
der positiven x-Achse, welche in Richtung der Spaltnormalen zeigt. Befindet
sich der Schirm in einer großen Entfernung l vom Spalt, d.h. l ≫ b, so hat
die von dem elementaren Spalt an der Stelle y ausgesandte Welle gegenüber
der von dem elementaren Spalt in der Spaltmitte ausgesandten Welle in Richtung θ einen Gangunterschied von y sin θ, siehe Abb. 8.2. Dies entspricht einer
Phasendifferenz φ von
2π
φ=
y sin θ =
λ
!
2π sin θ
y.
λ
(8.1)
In einem Punkt, der unter dem Winkel θ gegenüber der x-Achse auf dem
Schirm liegt, ist die elektrische Feldstärke, hervorgerufen von dem elementaren
Spalt an der Stelle y, damit gegeben durch
!
dy
dE = Ê0
cos(ωt − φ) .
b
(8.2)
Hierbei ist Ê0 (dy/b) die Amplitude der von einem beliebigen elementaren Spalt
ausgehenden Welle im Abstand l vom Entstehungsort. Sie ist proportional zu
dem Bruchteil dy/b, den der elementare Spalt der Breite dy bezogen auf die gesamte Spaltbreite b einnimmt, weil der Spalt durch die auftreffende ebene Welle
gleichmäßig zur Aussendung von Zylinderwellen angeregt wird. Da in Geradeausrichtung (θ = 0) alle Wellen in Phase sind (φ = 0), folgt aus Gl. (8.2) direkt,
daß Ê0 die Amplitude der vom gesamten Spalt herrührenden Welle im Zentrum des Schirms ist. Um die elektrische Feldstärke für einen beliebigen Punkt
auf dem Schirm zu berechnen, müssen wir die von den einzelnen elementaren
Spalten herrührenden Beiträge gemäß Gl. (8.2) aufintegrieren, wobei die Beziehung aus Gl. (8.1) zu berücksichtigen ist. Wir haben also in Gl. (8.2) über y
zu integrieren für einen festen Zeitpunkt t und für einen beliebigen, aber festen
Wert des Winkels θ, der die Lage des betrachteten Punktes auf dem Schirm
angibt. Die Integrationsgrenzen sind −b/2 und b/2. Die Integration vereinfacht sich, wenn wir die von den einzelnen elementaren Spalten herrührenden
Feldstärken zunächst komplex schreiben, dann aufsummieren und schließlich
wieder zum Realteil übergehen. Dies ist erlaubt, da der Realteil einer Summe
von komplexen Zahlen gleich der Summe der Realteile ist. Gl. (8.2) lautet in
167
8.2 Beugung am Spalt
komplexer Form
!
dy j(ωt−φ)
e
.
dE = Ê0
b
(8.3)
Die Integration über y liefert die elektrische Feldstärke E für einen beliebigen
Punkt des Schirms in komplexer Form
Ê0 Z b/2 j(ωt−φ)
e
dy .
b −b/2
E=
(8.4)
Der Phasenwinkel φ hängt gemäß Gl. (8.1) von y ab. Mit Hilfe der Substitutionsregel der Integralrechnung können wir die Integration über y durch eine
Integration über φ ersetzen. Aus Gl. (8.1) folgt die Beziehung
λ
dφ .
2π sin θ
dy =
(8.5)
Aus Gl. (8.1) ergibt sich weiter, daß für y = ±b/2 die Phasendifferenz φ die
Werte φ = ±(πb/λ) sin θ annimmt. Setzt man der Einfachheit halber
πb
sin θ ,
λ
(8.6)
Ê0 Z β j(ωt−φ)
e
dφ .
2β −β
(8.7)
β=
so liefert die Substitutionsregel
E=
Da t bezüglich der Integration über φ konstant ist, folgt
e−jφ
Ê0 jωt
Ê0 jωt Z β −jφ
−
e
e
e
dφ =
E =
2β
2β
j
−β
"
=
Ê0 jωt e
e
β
jβ
−e
2j
−jβ
!
= Ê0
#β
−β
sin β jωt
e .
β
(8.8)
Die elektrische Feldstärke in einem Punkt, der unter dem Winkel θ gegenüber
der x-Achse auf dem Schirm liegt, erhalten wir schließlich, wenn wir in Gl. (8.8)
den Realteil nehmen. Es ergibt sich
E = Ê0
sin β
cos(ωt) .
β
(8.9)
Für die Amplitude der elektrischen Feldstärke gilt offensichtlich
Ê(θ) = Ê0
sin β
β
(8.10)
168
8 Beugung
mit β = (πb/λ) sin θ. Wie wir wissen, ist die mittlere Intensität proportional
zum Quadrat der Amplitude der elektrischen Feldstärke, d.h. S ∼ Ê 2 . Für die
mittlere Intensität S (wir schreiben im folgenden der Kürze halber einfach S)
erhalten wir somit
sin2 β
S(θ) = S0 2 .
(8.11)
β
Die Abhängigkeit der Intensität S vom Winkel θ, der die Lage des Beobachtungspunktes auf dem Schirm beschreibt, ist enthalten in β wegen
β = (πb/λ) sin θ, wobei θ die Werte −π/2 ≤ θ ≤ π/2 annehmen kann. Weiterhin ist S0 die Intensität, die in Richtung θ = 0, also im Zentrum des Schirms zu
finden ist. Das läßt sich auf folgende Weise nachprüfen: Für θ → 0 gilt wegen
Gl. (8.6) β → 0 und damit sin β/β → 1. Aus Gl. (8.11) folgt dann S(0) = S0 .
Die durch Gl. (8.11) gegebene Intensitätsverteilung ist in Abb. 8.3 dargestellt.
S(θ)
S0 6
1
-
-3
-2
-1
0
1
2
3 (b/λ) sin θ
Abbildung 8.3: Intensitätsverteilung für die Beugung an einem Spalt
Wir wollen noch die Lage der Extrema der Intensitätsverteilung bestimmen.
Die Extremwerte der Funktion S(θ) treten für jene Werte von β auf, für die
die Ableitung dS/dβ = 0 ist. Dies liefert
dS
2 sin β(β cos β − sin β)
= S0
=0.
dβ
β3
(8.12)
169
8.2 Beugung am Spalt
Die Ableitung verschwindet zum einen, wenn sin β = 0 ist. Dies ist der Fall für
β = 0, bzw. wegen Gl. (8.6) für θ = 0. In dieser Richtung liegt das sogenannte Hauptmaximum der Intensitätsverteilung, siehe Abb. 8.3. Die Gleichung
sin β = 0 ist aber auch erfüllt für β = ±mπ mit m = 1, 2, 3, . . .. Aus Gl. (8.11)
folgt, daß für diese Werte von β die stets positive Intensität verschwindet, d.h.
S = 0. Mit β = (πb/λ) sin θ erhält man damit für die Winkel, bei denen die
Minima (Nullstellen) der Intensitätsverteilung auftreten, folgende Bedingung:
b sin θmin,m = ±mλ ,
m = 1, 2, 3, . . . ,
(8.13)
siehe auch Abb. 8.3. Die in Gl. (8.13) gewonnene Bedingung läßt sich auch
anschaulich interpretieren. Man denke sich dazu den gesamten Spalt in eine
gerade Zahl von 2m, m = 1, 2, 3, . . ., Teilspalten zerlegt. Befindet sich der Beobachtungspunkt in einer großen Entfernung vom Schirm, so haben in Richtung θ
die am Rand von zwei benachbarten Teilspalten ausgesandten Elementarwelb
len einen Gangunterschied von 2m
sin θ. Ist dieser Gangunterschied gerade λ/2,
so löschen sich in dieser Richtung immer je zwei Elementarwellen zweier benachbarter Teilspalte aus. Diese Bedingung liefert aber genau die Beziehung
in Gl. (8.13).
Die Ableitung in Gl. (8.12) verschwindet zum anderen für die Werte von β,
für die β cos β − sin β = 0 oder tan β = β gilt. Diese transzendente Gleichung
kann nur numerisch gelöst werden. Sie hat unendlich viele Lösungen. Die ersten lauten β = ±1, 43 π, ±2, 46 π, ±3, 47 π, . . .. In guter Näherung gilt die
Beziehung β ≈ ±(m + 1/2)π mit m = 1, 2, 3, . . .. Diese Näherung stimmt um
so besser, je größer die Werte von m sind. Der Leser möge sich dies anhand des
Graphen der Tangensfunktion klarmachen. Jeweils ein solcher Extremwert liegt
zwischen zwei benachbarten Minima, deren Lage ja durch β = ±mπ gegeben
ist. Es kann sich bei den zuletzt berechneten Extremwerten also nur um lokale
Maxima der Intensitätsverteilung handeln. Mit β = (πb/λ) sin θ erhält man für
die Winkel, bei denen die sogenannten Nebenmaxima der Intensitätsverteilung
auftreten, folgende Bedingung:
1
b sin θmax,m ≈ ±(m + )λ ,
2
m = 1, 2, 3, . . . ,
(8.14)
siehe auch Abb. 8.3. Auch die in Gl. (8.14) gewonnene Bedingung kann man
anschaulich interpretieren. Man denke sich dazu den gesamten Spalt in eine
ungerade Zahl von 2m + 1, m = 1, 2, 3, . . ., Teilspalten zerlegt. Befindet sich
der Beobachtungspunkt in einer großen Entfernung vom Schirm, so haben in
Richtung θ die am Rand von zwei benachbarten Teilspalten ausgesandten Eleb
sin θ. Ist dieser Gangunterschied
mentarwellen einen Gangunterschied von 2m+1
gerade λ/2, so löschen sich in dieser Richtung immer je zwei Elementarwellen
170
8 Beugung
zweier benachbarter Teilspalte aus. Da die Anzahl der Teilspalte ungerade ist,
bleibt einer übrig. Dessen Elementarwellen breiten sich ungehindert aus und
rufen so das m-te Nebenmaximum der Intensitätsverteilung hervor. Die oben
beschriebene Bedingung liefert aber genau die Beziehung in Gl. (8.14).
8.3
Beugung an einer kreisförmigen Öffnung
Ein für die Praxis sehr wichtiger Fall ist die FRAUNHOFERsche Beugung an
einer kreisförmigen Öffnung. Der Durchmesser der Öffnung sei d. Aus Symmetriegründen ist klar, daß das Beugungsmuster rotationssymmetrisch sein muß.
Es besteht aus einem hellen, kreisförmigen Fleck in der Mitte, der abwechselnd
von dunklen und hellen konzentrischen Ringen umgeben ist. Die Intensität der
hellen Ringe nimmt mit zunehmendem Abstand vom Zentrum nach außen
hin rasch ab. Der helle Fleck in der Mitte, der das Hauptmaximum der Intensitätsverteilung darstellt, wird als AIRYsches Beugungsscheibchen bezeichnet. Die mathematische Berechung der Intensitätsverteilung wurde erstmals
1835 von G. B. AIRY (1801 - 1892) durchgeführt und beinhaltet die BESSELFunktionen. Der Winkel, unter dem das erste Intensitätsminimum, also der
erste dunkle Ring auftritt, ist gegeben durch
sin θmin,1 = 1, 22
λ
.
d
(8.15)
Alle optischen Instrumente, wie z.B. Fernrohr, Mikroskop und auch das
menschliche Auge, haben ein begrenztes Auflösungsvermögen. Das bedeutet,
daß eng beieinanderliegende Punkte eines Objektes nicht mehr getrennt abgebildet werden. Ursache für das endliche Auflösungsvermögen ist die Beugung
des Lichtes beispielsweise an Blenden oder Linseneinfassungen. Betrachtet man
etwa mit einem Fernrohr einen Fixstern, dann würde man nach den Gesetzen der geometrischen Optik als Bild einen Lichtpunkt erwarten. Tatsächlich
erhält man aber infolge der Beugung an der Objektivöffnung ein AIRYsches
Beugungsscheibchen mit endlichem Durchmesser, umgeben von konzentrischen
Ringen mit rasch abnehmender Intensität. Wenn man zwei benachbarte Fixsterne betrachtet, erhält man zwei Beugungsscheibchen, die selbstverständlich
nur dann getrennt wahrgenommen werden, wenn sie einen bestimmten Mindestabstand voneinander haben. Ist der Abstand zu klein, so verschwimmen
beide Beugungsscheibchen zu einem Fleck, und dem Beobachter erscheinen die
beiden Sterne als lediglich einer.
Die Frage, welchen Abstand die Beugungsscheibchen für eine sichere
Auflösung haben müssen, läßt sich nicht eindeutig beantworten. Meist wird das
171
8.4 Beugung am Gitter
RAYLEIGHsche Kriterium zugrunde gelegt. Nach LORD RAYLEIGH (1842 1912) lassen sich zwei Objekte sicher trennen, wenn das Zentrum des AIRYschen Beugungsscheibchens des einen Objekts in den ersten dunklen Ring des
Beugungsmusters des anderen Objekts fällt. Mit Hilfe von Gl. (8.15) folgt,
daß zwei Objektpunkte dann noch aufgelöst werden, wenn für den Winkelabstand ∆θ, unter dem sie erscheinen,
λ
(8.16)
d
gilt. Hierbei ist d der Objektiv- bzw. Blendendurchmesser des jeweiligen optischen Instruments.
∆θ ≈ sin ∆θ ≥ 1, 22
8.4
Beugung am Gitter
In diesem Abschnitt wollen wir die FRAUNHOFERsche Beugung an einem
Gitter betrachten und das zugehörige Beugungsmuster berechnen. Ein Gitter
besteht aus einer großen Zahl von parallelen Spalten, die sich in einem ansonsten lichtundurchlässigen Material befinden. Alle Spalte mögen den gleichen
Abstand g voneinander haben, der auch als Gitterkonstante bezeichnet wird.
Solche Gitter werden in der Praxis hergestellt, indem man in eine planparallele Glasplatte in gleichen Abständen parallele Furchen ritzt. Die unversehrten,
äußerst schmalen Glasstreifen wirken dann wie lichtdurchlässige Spalte. Die
Gitterkonstante ist üblicherweise klein, z.B. 2 µm, und die Zahl der Gitterspalte ist in der Regel groß, z.B. 10000. Das Gitter werde mit linear polarisiertem
Licht der Wellenlänge λ beleuchtet. In Abb. 8.4 ist ein solches Gitter dargestellt. In der Richtung senkrecht zur Zeichenebene seien die Spalte sehr weit
ausgedehnt verglichen mit ihrer Breite. Der Einfachheit halber wollen wir die
Breite der einzelnen Spalte als vernachlässigbar klein annehmen, so daß wir
Beugungseffekte, die von den einzelnen Spalten herrühren, nicht zu betrachten brauchen. Wir können die von den einzelnen Spalten ausgehenden Wellen
somit als Zylinderwellen ansehen. Die Überlagerung dieser Zylinderwellen in
den verschiedenen Richtungen soll im folgenden berechnet werden. Die Richtungen werden wieder angegeben durch den Winkel θ gegenüber der positiven
x-Achse, welche in Richtung der Gitternormalen zeigt. Das Gitter bestehe aus
N Spalten. Befindet sich der Schirm in einer großen Entfernung l von dem
Gitter, d.h. l ≫ g, so haben die von zwei benachbarten Spalten ausgesandten
Wellen in Richtung θ einen Gangunterschied von g sin θ, siehe Abb. 8.4. Dies
entspricht einer Phasendifferenz φ von
φ=
2π
g sin θ .
λ
(8.17)
172
8 Beugung
?
6
g
?
6
g
?
6
1
θ
θ
g sin θ
1
1
l
g sin θ
Abbildung 8.4: FRAUNHOFERsche Beugung an einem Gitter
In einem Punkt, der unter dem Winkel θ gegenüber der x-Achse auf dem
Schirm liegt, ist die elektrische Feldstärke, hervorgerufen von dem n-ten Spalt,
damit gegeben durch
En = Ê0 cos(ωt − nφ) ,
n = 0, 1, 2, . . . , N − 1 .
(8.18)
Hierbei ist Ê0 die Amplitude der von einem einzelnen Spalt ausgehenden Welle im Abstand l vom Entstehungsort. Diese Amplitude ist für alle Spalte die
gleiche, weil die einzelnen Gitterspalte durch die auftreffende ebene Welle
gleichmäßig zur Aussendung von Zylinderwellen angeregt werden. Da in Geradeausrichtung (θ = 0) alle Wellen in Phase sind (φ = 0), folgt sofort, daß die
Amplitude der von allen Spalten herrührenden Welle im Zentrum des Schirms
N Ê0 ist. Um die elektrische Feldstärke für einen beliebigen Punkt auf dem
Schirm zu berechnen, müssen wir die von den einzelnen Spalten herrührenden Beiträge gemäß Gl. (8.18) aufsummieren. Die Summation vereinfacht sich,
wenn wir die von den einzelnen Spalten herrührenden Feldstärken zunächst
komplex schreiben, dann aufsummieren und schließlich wieder zum Realteil
übergehen. Gl. (8.18) lautet in komplexer Form
En = Ê0 ej(ωt−nφ) ,
n = 0, 1, 2, . . . , N − 1 .
(8.19)
173
8.4 Beugung am Gitter
Die Summation über n ergibt
E=
N
−1
X
Ê0 ej(ωt−nφ) = Ê0 ejωt
N
−1
X
e−jnφ = Ê0 ejωt
e−jφ
n=0
n=0
n=0
N
−1 X
n
.
(8.20)
Mit Hilfe der Beziehung
1 + z + z 2 + · · · + z N −1 =
zN − 1
z−1
folgt weiter
E = Ê0 e
jωt

e−jN φ − 1
e−jφ − 1
= Ê0 ejωt 
= Ê0 e
= Ê0
!
e−jN φ/2 e−jN φ/2 − ejN φ/2
e−jφ/2 (e−jφ/2 − ejφ/2 )
ejN φ/2 − e−jN φ/2
ejφ/2 − e−jφ/2
j(ωt−(N −1)φ/2)
sin N φ2
sin


!
ej(ωt−(N −1)φ/2) .
φ
2
(8.21)
Die elektrische Feldstärke in einem Punkt, der unter dem Winkel θ gegenüber
der x-Achse auf dem Schirm liegt, erhalten wir, wenn wir in Gl. (8.21) zum
Realteil übergehen. Es ergibt sich
E = Ê0
sin N φ2
φ
cos ωt − (N − 1)
2
sin φ
2
!
.
(8.22)
Für die Amplitude der elektrischen Feldstärke gilt offensichtlich
Ê(θ) = Ê0
sin N φ2
sin
φ
2
(8.23)
mit φ = (2π/λ)g sin θ. Die Intensität erhalten wir schließlich durch Quadrieren
von Gl. (8.23). Das liefert
S(θ) = S0
sin2 N φ2
sin2
.
φ
2
(8.24)
174
8 Beugung
Die Abhängigkeit der Intensität vom Winkel θ, der die Lage des Beobachtungspunktes auf dem Schirm beschreibt, ist enthalten in φ wegen φ = (2π/λ)g sin θ,
wobei θ die Werte −π/2 ≤ θ ≤ π/2 annehmen kann. Weiterhin ist S0 die Intensität, die ein einzelner Spalt in Richtung θ = 0, also im Zentrum des Schirms
hervorruft. Die durch Gl. (8.24) gegebene Intensitätsverteilung ist in Abb. 8.5
dargestellt. Eine ausführliche Kurvendiskussion der Funktion S(θ) kann hier
S(θ)
S0 6
N2
-
− 76
−1
− 65
− 64
− 36
− 26
− 61
0
1
6
2
6
3
6
4
6
5
6
1
(g/λ) sin θ
Abbildung 8.5: Intensitätsverteilung für die Beugung an einem Gitter (N = 6)
nicht durchgeführt werden. Es zeigt sich, daß die Intensität maximal wird,
wenn der Nenner in Gl. (8.24) verschwindet. Dies ist der Fall, für φ = ±m2π
mit m = 0, 1, 2, . . .. Für diese Werte von φ nimmt die Intensität S den Wert
N 2 S0 an, denn es gilt sin2 (N φ/2)/ sin2 (φ/2) → N 2 , für φ → ±m2π (Übungsaufgabe). Wegen φ = (2π/λ)g sin θ, erhält man damit für die Winkel, bei denen
die Hauptmaxima der Intensitätsverteilung auftreten, folgende Bedingung:
g sin θmax,m = ±mλ ,
m = 0, 1, 2, . . . ,
(8.25)
siehe auch Abb. 8.5. Die Lage der Hauptmaxima ist offensichtlich unabhängigvon der Zahl N der Gitterspalte. Die in Gl. (8.25) gewonnene Bedingung läßt
sich auch anschaulich interpretieren. Befindet sich der Beobachtungspunkt in
175
8.4 Beugung am Gitter
einer großen Entfernung vom Schirm, so haben in Richtung θ die von zwei
benachbarten Spalten ausgehenden Wellen einen Gangunterschied von g sin θ.
Ist dieser Gangunterschied gerade ein ganzzahliges Vielfaches von λ, so ergibt
sich konstruktive Interferenz für alle von den einzelnen Spalten ausgesandten
Wellen. Diese Bedingung liefert aber genau die Beziehung in Gl. (8.25).
Zwischen je zwei Hauptmaxima liegen N − 1 Nebenminima. Die stets positive Intensität hat dort den Wert Null. Die Nebenminima treten also auf,
wenn in Gl. (8.24) lediglich der Zähler verschwindet. Dies ist der Fall, wenn φ
die Werte φ = ±k2π/N annimmt mit k = 1, . . . , N − 1, N + 1, . . . , 2N − 1,
2N + 1, . . .. Wegen φ = (2π/λ)g sin θ, erhält man für die Winkel, bei denen
die Nebenminima der Intensitätsverteilung auftreten, folgende Bedingung:
g sin θmin,k
k
=± λ,
N


1,


. . . , N − 1,
k =  N + 1, . . . , 2N − 1,
..


.
(8.26)
siehe auch Abb. 8.5. Die N − 1 Nebenminima sind wiederum durch N − 2 Nebenmaxima voneinander getrennt. Mit steigender Spaltanzahl N werden die
Hauptmaxima immer schmaler aber auch immer höher. Die Breite der Hauptmaxima nimmt proportional 1/N ab, die Höhe proportional N 2 zu. Die Höhe
der Nebenmaxima wird im Vergleich zur Höhe der Hauptmaxima mit wachsendem N immer geringer. Da die in der Praxis verwendeten Gitter üblicherweise
ein große Anzahl von Spalten haben, sind die Nebenmaxima auf dem Schirm
meist gar nicht sichtbar, und das Beugungsmuster besteht lediglich aus scharfen Linien, die den Hauptmaxima entsprechen.
Eine wichtige Anwendung von Gittern besteht in der spektralen Zerlegung
von Licht. Wird ein Gitter nicht mit monochromatischem Licht, sondern Licht
verschiedener Wellenlängen durchstrahlt, so treten gemäß Gl. (8.25) die Hauptmaxima für die einzelnen Wellenlängen bei verschiedenen Winkeln auf. Der
entscheidende Punkt dabei ist, welchen Wellenlängenunterschied das Gitter
noch aufzulösen vermag. Als Bedingung für die Auflösung wird wieder das
RAYLEIGHsche Kriterium zugrunde gelegt. Dabei geht man davon aus, daß
die Hauptmaxima von zwei dicht benachbarten Wellenlängen λ und λ + ∆λ in
m-ter Beugungsordnung gerade noch getrennt werden, wenn das m-te Hauptmaximum der Wellenlänge λ + ∆λ auf das direkt neben dem m-ten Hauptmaximum der Wellenlänge λ liegende Nebenminimum fällt. Mit den Gln. (8.25)
und (8.26) liefert das die Beziehung
m(λ + ∆λ) =
mN + 1
λ.
N
(8.27)
176
8 Beugung
Eine einfache Umformung ergibt
λ
= mN .
∆λ
(8.28)
Den Quotienten aus der Wellenlänge λ des untersuchten Lichtes und der kleinsten Wellenlängendifferenz ∆λ, die noch getrennt werden kann, bezeichnet man
allgemein als das spektrale Auflösungsvermögen A eines Spektralapparates, in
Zeichen
λ
.
(8.29)
A=
∆λ
Aus Gl. (8.28) folgt damit für das spektrale Auflösungsvermögen eines Gitters
A = mN .
(8.30)
Wir haben bei der Berechnung der Intensitätsverteilung für die Beugung
an einem Gitter der Einfachheit halber angenommen, daß die Breite der Einzelspalte vernachlässigbar klein ist. Berücksichtigt man die endliche Breite b
der Einzelspalte, so ergibt sich ein ähnliches Beugungsmuster wie das gemäß
Gl. (8.24) bzw. Abb. 8.5. Die Intensität der Hauptmaxima nimmt aber mit
wachsender Beugungsordnung m ab, und zwar um so schneller, je breiter die
Einzelspalte sind. Dies ist bei der spektralen Zerlegung von Licht mit Hilfe eines Gitters zu berücksichtigen. Das spektrale Auflösungsvermögen nimmt mit
wachsender Beugungsordnung zwar zu, die Intensität wird aber geringer. Im
Experiment hat man somit ein Optimum zu suchen.
Anhang A
Aufgaben mit Lösungen
Hinweis: Bei den folgenden Aufgaben wird für die Erdbeschleunigung stets
der Wert g = 9, 81 m s−2 benutzt.
Aufgaben zu Kapitel 1
Aufgabe 1.1: Nach BOHR wird der Kern eines H-Atoms, bestehend aus einem Proton (Ladung: +e), von einem Elektron (Ladung: −e) umkreist. Dieses
hat im Grundzustand vom Kern den Abstand 52, 9 pm.
(a) Mit welcher COULOMB-Kraft ziehen sich das Elektron und das Proton
des Wasserstoffkerns auf Grund ihrer Ladungen an?
(b) Außerdem ziehen sich das Elektron (Masse: me = 0, 911 · 10−30 kg) und das
Proton (Masse: mp = 1, 673 · 10−27 kg) wie alle Massen nach dem NEWTONschen Gravitationsgesetz mit der Kraft
me mp
FG = G
r2
an. Hierbei ist G = 6, 672 · 10−11 N m2 kg−2 die universelle Gravitationskonstante. Wieviel mal so groß ist die COULOMB-Kraft wie die Gravitationskraft? Lösung : (a) 8, 24 · 10−8 N, (b) 2, 27 · 1039 .
Aufgabe 1.2: Es befinden sich im Punkt ~r1 = (x1 , y1 ) = (0 cm, 5 cm) eine Ladung q1 = 1 µC, im Punkt ~r2 = (x2 , y2 ) = (−10 cm, 0 cm) eine Ladung
q2 = 4 µC und im Punkt ~r = (x, y) = (0 cm, 0 cm) eine Ladung q = −2 µC.
Berechnen Sie die resultierende Kraft, welche die Ladungen q1 und q2 auf die
Ladung q ausüben, und zwar
(a) als Vektor,
(b) Betrag und den Winkel, den die Kraft mit der x-Achse einschließt.
Lösung : (a) F~ = (Fx , Fy ) = (−7, 19 N, 7, 19 N), (b) F = 10, 17 N; α = 1350 .
177
178
ANHANG A. AUFGABEN MIT LÖSUNGEN
Aufgabe 1.3: Es befinden sich im Punkt ~r1 = (x1 , y1 ) = (3 cm, 4 cm) eine Ladung q1 = 2 µC, im Punkt ~r2 = (x2 , y2 ) = (−12 cm, 5 cm) eine Ladung
q2 = −3 µC und im Punkt ~r = (x, y) = (0 cm, 0 cm) eine Ladung q = 5 µC.
Berechnen Sie die resultierende Kraft, welche die Ladungen q1 und q2 auf die
Ladung q ausüben, und zwar
(a) als Vektor,
(b) Betrag und den Winkel, den die Kraft mit der x-Achse einschließt.
Lösung : (a) F~ = (Fx , Fy ) = (−28, 9 N, −25, 7 N),
(b) F = 38, 7 N; α = 221, 60 .
Aufgabe 1.4: Berechnen Sie die elektrische Feldstärke, welche die Ladung q1
und q2 im Punkt (x; y) = (0; 0) hervorrufen,
(a) Im Falle der Aufgabe 1.2,
(b) Im Falle der Aufgabe 1.3,
~ = (Ex , Ey ) = (3, 6 MV , −3, 6 MV ); E = 5, 1 MV ; α = 3150 ,
Lösung : (a) E
m
m
m
MV
MV
MV
~
(b) E = (Ex , Ey ) = (−5, 78 m , −5, 14 m ); E = 7, 74 m ; α = 221, 60
Aufgabe 1.5: Unter einem elektrischen Dipol versteht man zwei Ladungen
verschiedenen Vorzeichens, aber gleichen Betrages, die einen Abstand d voneinander haben. Die Ladung q (mit q > 0) liege im Punkt (x1 , y1 ) = ( d2 , 0),
die Ladung −q im Punkt (x2 , y2 ) = (− d2 , 0). Berechnen Sie die elektrische
Feldstärke des Dipols in den Punkten
(a) (x3 , y3 ) = (a, 0) mit a > d2 ,
(b) (x4 , y4 ) = (0, b) mit b ≥ 0,
(c) (x5 , y5 ) = (0, 0),
(d) (x6 , y6 ) = ( d2 , b).
(e) Skizzieren Sie die in a bis d berechneten Feldstärken, in der x, y−Ebene,
ebenso die Feldstärken in den Punkten (−a, 0), (0, −b), (− d2 , b), (− d2 , −b),
( d2 , −b).
Aufgabe 1.6: Berechnen Sie die elektrischen Flüsse durch die Flächen A1 und A2 im
Falle der nebenstehenden Abbildung, wenn
(a) q1 = 3 nC, q2 = −5 nC, q3 = 8 nC
(b) q1 = 3 nC, q2 = −5 nC, q3 = 2 nC
(c) q1 = 3 nC, q2 = −5 nC, q3 = −3 nC
Lösung : (a) 6 nC/ε0 ; 11 nC/ε0 , (b) 0;
5 nC/ε0 , (c) −5 nC/ε0 ; 0.
Aufgabe 1.7: Im Vakuum bewegt sich in einem homogenen elektrischen Feld
vom Betrag 10 kV
ein Elektron vom Nullpunkt (x = 0) zu einem Punkt mit
cm
179
der Koordinate x = 2 cm. Berechnen Sie mit Hilfe des Energieerhaltungssatzes
(a) die kinetische Energie des Elektrons im Punkt x = 2 cm, wenn es im Nullpunkt die Geschwindigkeit 0 gehabt hat. Geben Sie die kinetische Energie
dabei sowohl in Joule als auch in eV an. (1 eV = 1, 602 · 10−19 J)
(b) die Geschwindigkeit des Elektrons im Punkt x = 2 cm.
Lösung : (a) 3, 2 · 10−15 J; 20 keV, (b) 8, 39 · 107 ms
Aufgabe 1.8: Berechnen Sie das Potential, das der Zielort (x = 2 cm) in
Aufgabe 1.7 hat, wenn dem Ausgangsort (x = 0) das Potential 0 zugeordnet
wird, sowie die Spannung des Ausgangsortes (x = 0) gegenüber dem Zielort
(x = 2 cm).
Lösung : 20 kV; −20 kV
Aufgabe 1.9: Welche Spannung muss ein Elektron durchlaufen, um von der
Geschwindigkeit 0 auf die Geschwindigkeit 107 ms beschleunigt zu werden?
Lösung : 284 V
Aufgabe 1.10: Der Punkt B hat gegenüber dem Punkt A eine Spannung
von 1 kV. Welche Geschwindigkeit hat im Punkt B
(a) ein Elektron, das in A die Geschwindigkeit 107 ms hatte,
(b) ein Proton , das in A die Geschwindigkeit 5 · 105 ms hatte,
wenn beide Teilchen von A nach B fliegen?
Lösung : (a) 2, 125 · 107 ms , (b) 2, 418 · 105 ms
Aufgabe 1.11: (a) Berechnen Sie die (punktförmige) Ladung, die in 5 cm
Abstand ein Potential von 2 V erzeugt.
(b) Welche Radien haben dann die Äquipotentialflächen 4 V, 6 V, 8 V, 10 V?
(c) Zeichnen Sie die Äquipotentialflächen 2 V, 4 V, 6 V, 8 V, 10 V.
(d) Welche Spannung hat ein beliebiger Punkt der Äquipotentialfläche 8 V
gegenüber einem beliebigen Punkt der Äquipotentialfläche 6 V?
Lösung : (a) 1, 11 · 10−11 C, (b) 2,5 cm; 1,67 cm; 1,25 cm; 1 cm, (d) 2 V.
Aufgabe 1.12: Berechnen Sie
(a) das elektrische Potential, dass der Wasserstoffkern am Ort des Wasserstoffelektrons im Grundzustand verursacht (r = 52, 9 pm),
(b) die potentielle Energie Ep in eV des Elektrons im Grundzustand,
(c) die Gesamtenergie
E = Ep +
1
me v 2
2
des Elektrons in eV.
Hinweis: Auf der Kreisbahn des Elektrons besteht ein Kräftegleichgewicht zwi-
180
ANHANG A. AUFGABEN MIT LÖSUNGEN
schen der COULOMB-Kraft und der Zentrifugalkraft, in Zeichen
e2
v2
=
m
e
4 π ε0 r 2
r
Lösung : (a) 27, 2 V, (b) −27, 2eV, (c) −13, 6eV.
Aufgabe 1.13: Berechnen Sie die aufzuwendende Arbeit, um zwei gleichartige punktförmige Ladungen von je 10−5 C von einer Entfernung r1 = 1 m auf
r2 = 0, 1m zu nähern.
Lösung : 8, 09 J.
Aufgaben zu Kapitel 2
Aufgabe 2.1: In einem unendlich langen Zylinder vom Radius R ist die
Ladung gleichmäßig über das gesamte Volumen verteilt. ̺ sei die Raumladungsdichte. Zeigen Sie, dass für die elektrische Feldstärke im Abstand r von
der Zylinderachse gilt:
(a)
̺r
E=
, wenn r ≤ R,
2 ε0
(b)
E=
̺ R2
2 ε0 r
, wenn r ≥ R.
Aufgabe 2.2: Die Potentiale zweier Äquipotentialflächen einer geladenen
Ebene unterscheiden sich um 5 V, wenn sie einen Abstand von 1 cm voneinader
haben. Berechnen Sie die Flächenladungsdichte der geladenen Ebene.
nC
Lösung : 8, 85 m
2
Aufgabe 2.3: Zwei isolierte, leitende, weit voneinader entfernte Kugeln mit
den Radien R1 und R2 tragen Ladungen Q1 und Q2 . Es ist zu zeigen, dass die
Neuverteilung (!) der Ladungen, die sich bei einer leitenden Verbindung der
Kugeln ergibt, auf ihnen das Potential
ϕ=
Q1 + Q2
4 π ε0 (R1 + R2 )
erzeugt.
Aufgabe 2.4: Die Hochspannungselektrode eines elektrostatischen Spannungsgenerators ist eine metallische Kugelschale, die auf 9 MV Potential liegt.
181
(a) Elektrischer Durchschlag tritt im Gas dieses Generators bei Feldern von
100 MV
auf. Welche Forderung muss an den Radius R der Kugelschale gestellt
m
werden, damit ein elektrischer Durchschlag vermieden wird?
zur Kugel, um Leckströme
(b) Ein langes Gummiband transportiert 0, 3 mC
s
zu kompensieren. Welche Leistung ist mindestens für diesen Ladungstransport
erforderlich?
Lösung : (a) R > 9 cm, (b) 2, 7 kW
Aufgabe 2.5: (a) Berechnen Sie die Kapazität eines Plattenkondensators,
dessen Platten sich im Vakuum befinden, kreisförmig sind (Durchmesser:
40 cm), sowie den Abstand von 1 cm voneinander haben.
(b) Welche Ladung kann (auf der positiven Platte) im Kondensators gespeichert werden, wenn die Spannung zwischen den Platten 220 V beträgt?
(c) Wie groß ist die elektrische Feldstärke des Kondensators?
(d) Welche Kapazität hat der Kondensator, wenn zwischen seinen Platten ein
Phenolharzpressstoff mit der Dielektrizitätskonstanten (relative Permittivität)
12 gebracht wird?
Lösung : (a) 111 pF, (b) 24, 5 nC, (c) 22 kV
, (d) 1, 34 nF
m
Aufgabe 2.6: Zwei Platten eines Kondensators haben 1, 05 cm Abstand voneinander. Zwischen beiden Platten bringt man parallel eine weitere Platte (aus
Metall), so dass sie von der einen Kondensatorplatte 0, 4 cm entfernt ist. Das
Potential der nächstgelegen Kondensatorplatte habe den Wert 50 V, das der
anderen Platte −60 V. Berechnen sie das Potential der eingeschobenen Metallplatte, deren Dicke 0, 05 cm beträgt.
Lösung : 6 V
Aufgabe 2.7: Zeigen Sie, dass die Kapazität
(a) eines Kugelkondensators (Innenradius ri , Außenradius ra ),
(b) eines Zylinderkondensators (Innenradius ri , Außenradius ra ),
C = ε0 Ad wird, wenn für den Abstand d = ra − ri der Kondensatorflächen
d = ra − ri ≪ ri gilt, und damit beide Elektrodenflächen (näherungsweise) den
selben Wert A haben.
Hinweis zu (b): Es gilt ln(1 + x) = x, für |x| ≪ 1.
Aufgabe 2.8: Ein Wickelkondensator besteht aus zwei 5 cm breiten Bändern
aus Aluminiumfolie, die durch Paraffinpapier (Dicke: 0, 03 mm, Dielektrizitätszahl: 2,4) isoliert sind. Wie lang müssen die Bänder sein, damit die Kapazität
4 µF beträgt?
Lösung : 56, 5 m
Aufgabe 2.9: Der Füllstand x eines Ölbehälters (die Dielektrizitätszahl des
182
ANHANG A. AUFGABEN MIT LÖSUNGEN
Öls ist ε) lässt sich mit Hilfe der Kapazität C eines Plattenkondensators (Plattenhöhe: h, Plattenbreite: b, Plattenabstand: d) bestimmen, der sich in dem
Behälter befindet (siehe Abbildung).
(a) Zeigen Sie, dass die Füllhöhe x gegeben ist durch
x=
Cd
ε0 b
−h
ε−1
(b) Zwischen welchen Werten liegt die Kapzität, wenn ε = 3, 5; h = 0, 8 m;
b = 5 cm; d = 1 cm; 0 ≤ x ≤ 0, 6 m?
Lösung : (b) 35, 4 pF ≤ C ≤ 101, 8 pF
Aufgabe 2.10: Ein Drehkondensator besteht aus einer Anzahl halbkreisförmiger Platten vom Radius r (siehe Abbildung).
(a) Wie viele Platten werden benötigt, wenn der Abstand zwischen zwei benachbarten Platten 1 mm und der Kreisradius 5 cm betragen und bei voll
eingedrehten Platten eine Kapazität von mindestens 250 pF erreicht werden
soll?
(b) Welche Spannung darf an den Kondensator höchstens angelegt werden,
wenn die Feldstärke aus Sicherheitsgründen nicht größer als 50% der Durchschlagsfeldstärke 20 kV
werden soll?
cm
Lösung : (a) 9 Platten, (b) 1 kV
183
Aufgabe 2.11: Zu einer vorhandenen Kapazität C1 soll eine zweite Kapazität
C2 in Reihe geschaltet werden, so dass resultierende Kapazität C auf den Wert
k C1 verkleinert wird.
(a) Berechnen sie C2 als Funktion von C1 und k.
(b) Wie groß ist C2 , wenn k = 0, 6 und C1 = 10 nF?
Lösung : (a) C2 = 1k−C1k , (b) 15 nF
Aufgabe 2.12: Ein Plattenkondensator enthält ein Dielektrikum mit der
Dielektrizitätszahl 3 und hat einen Plattenabstand von 2 mm, sowie Platten
mit 1500 cm2 Fläche (jeweils).
(a) Wie groß ist seine Kapazität?
(b) Welche Energie enthält der Kondensator, wenn er auf 1000 V aufgeladen
ist?
(c) Wie groß ist die Energiedichte im Kondensator?
(d) Mit welcher Kraft ziehen sich die beiden Platten an?
Lösung : (a) 1,99 nF, (b) 0,996 mJ, (c) 3,32 mJ3 , (d) 0,498 N
Aufgaben zu Kapitel 3
Aufgabe 3.1: Ein Chrom-Nickel-Draht mit dem Radius 0, 65 mm hat einen
spezifischen Widerstand von ̺ = 1 · 10−6 Ω m. Wie lang muss der Draht sein,
damit sein Widerstand 2 Ω beträgt?
Lösung : 2, 66 m
Aufgabe 3.2: Kupfer ist ein einwertiges Metall, d.h. pro Atom trägt ein
Elektron zur elektrischen Leitfähigkeit bei. Kupfer hat bei 20 ◦ C die Dichte
8, 9 cmg 3 und den spezifischen Widerstand ̺ = 1, 70 · 10−6 Ω cm. Die Molmasse
g
von Kupfer beträgt Mmol = 63, 55 mol
. Berechnen Sie für die Leitungselektronen:
(a) die Anzahldichte der Leitungselektronen,
(b) deren Beweglichkeit,
(c) deren mittlere freie Flugzeit,
A
(d) deren Driftgeschwindigkeit bei einer Stromdichte von 6 mm
2
2
cm
−14
22
−3
s, (d) 0, 44 mm
Lösung : (a) 8, 43 · 10 cm , (b) 43, 5 Vs , (c) 2, 47 · 10
s
Aufgabe 3.3: Ein 10-kΩ-Kohlewiderstand mit einer spezifizierten Leistung
von 0, 25 W werde in einer elektronischen Schaltung eingesetzt. Wie groß ist
(a) die maximal zulässige Stromstärke,
(b) die maximal zulässige Spannung?
Lösung : (a) 5 mA, (b) 50 V
184
ANHANG A. AUFGABEN MIT LÖSUNGEN
Aufgabe 3.4: Betrachten Sie das in der Abbildung dargestellte Netzwerk.
Die Spannung betrage U = 10 V. Die Widerstände haben die Werte R1 = 1 Ω,
R2 = 2 Ω und R3 = 3 Ω. Berechnen Sie die Ströme I1 , I2 und I3 .
Lösung : I1 = 4, 55 A, I2 = 2, 73 A, I3 = 1, 82 A
Aufgaben zu Kapitel 4
~
Aufgabe 4.1: Messung des Magnetfeldes B
nach Thomas, Driscoll und Hipple.
(a) Eine Spule mit N rechteckigen Windungen befindet sich entsprechend der Abbil~ Im
dung zum Teil in einem Magnetfeld B.
Bereich der unteren, horizontalen Windungsteile der Länge l ist das Magnetfeld homogen.
Die Spule hängt an einer Waagschale. Die
Waage ist in ihrer Nullstellung, wenn durch
die Spule kein Strom fließt. Fließt ein Strom
I in der angegebenen Richtung, muss auf die
rechte Waagschale eine Masse m gelegt werden, damit sich der Waagebalken horizontal
stellt. Wie groß ist demnach B (allgemeine
Formel)?
(b) Welcher Wert ergibt sich für B, wenn
N = 9; I = 0, 1 A; l = 10 cm; m = 4, 5 g?
Lösung : (b) 0, 49 T
185
Aufgabe 4.2: Durch zwei lange, gerade
und parallele Leiter fließt der Strom I in die
gleiche Richtung (siehe Abbildung). Der Abstand der Leiter sei 2 a.
~ in der
(a) Berechnen Sie das Magnetfeld B
Ebene x = 0 als Funktion von y.
(b) Bei welchem y ist das Magnetfeld in der
Ebene x = 0 maximal und welchen Wert hat
es dort?
Iy
~
Lösung : (a) B(y)
= π (yµ02 +a
ex , (b) y = ±a,
2) ~
µ
I
~
B(±a)
= ± 0 ~ex
2πa
Aufgabe 4.3: Berechnen Sie mit Hilfe des BIOT-SAVARTschen Gesetzes das
Magnetfeld einer kreisförmigen Leiterschleife auf deren Symmetrieachse. Der
Strom durch die Leiterschleife sei I und der Radius der Leiterschleife sei R.
Zeigen Sie, dass das Magnetfeld auf der Symmetrieachse gegeben ist durch
B(x) =
R2
µ0 I
.
2 (R2 + x2 )3/2
Hierbei ist x der Abstand vom Mittelpunkt der Leiterschleife.
Aufgabe 4.4: (a) Berechnen Sie das Magnetfeld einer einlagigen, dicht gewickelten Spule auf deren Symmetrieachse. Die Spule habe N Wicklungen, die
Länge l und einen kreisförmigen Querschnitt mit dem Radius R. Zeigen Sie,
dass das Magnetfeld auf der Symmetrieachse der Spule gegeben ist durch


x − 2l
x + 2l
µ0 N I 
 .
q
B(x) =
−q
l 2
l 2
2
2
2l
R + (x + 2 )
R + (x − 2 )
Hierbei bezeichnet x den Abstand vom Mittelpunkt der Spule.
Hinweis: Verwenden Sie das Ergebnis der vorherigen Aufgabe und integrieren
Sie die Anteile zum Magnetfeld auf, die von den einzelnen kreisförmigen Wicklungen der Spule herrühren.
(b) Berechnen Sie das Magnetfeld insbesondere in der Spulenmitte (x = 0) und
an den Spulenenden (x = ±l/2) für verschiedene Werte von l: l = R, l = 4 R,
l = 10 R.
(c) Zeigen Sie außerdem, dass bei fester Wicklungsdichte n = N/l im Limes
l → ∞ für alle x gilt:
B(x) = µ0 n I .
Aufgabe 4.5: Berechnen Sie mit Hilfe des AMPEREschen Gesetzes (Durchflutungsgesetz) das Magnetfeld einer ringförmigen Spule (auch toroidale Spule
186
ANHANG A. AUFGABEN MIT LÖSUNGEN
genannt). Die Spule habe N Windungen und der Strom durch die Spule sei I.
Zeigen Sie, dass das Magnetfeld im Innern der Ringspule gegeben ist durch
B(r) =
µ0 N I
,
2πr
wobei r den radialen Abstand vom Zentrum der Ringspule bezeichnet, und dass
das Magnetfeld außerhalb der Spule verschwindet. Derartige Spulen werden
u.a. bei Fusionsreaktoren eingesetzt.
Aufgabe 4.6: Zwei koaxiale, kreisförmige Leiter haben einen Abstand d,
der ihrem Radius (R = 4, 0 cm) entspricht, und werden vom gleichen Strom
(I = 10 A) gleichsinnig durchflossen (Prinzip der Helmholtz-Spule). Wie groß
ist das magnetische Feld auf der gemeinsamen Achse
(a) in der Mitte zwischen den kreisförmigen Leitern,
(b) im Abstand R/4 von der Mitte entfernt?
(c) im Abstand R/2 von der Mitte entfernt?
Lösung : (a) 0, 225 mT, (b) 0, 224 mT (c) 0, 213 mT
Aufgabe 4.7: Noch eine Betrachtung zu
Helmholtz-Spulen: Sie bestehen aus zwei gleichen, kurzen, dünnlagigen, koaxialen Zylinderspulen (Windungszahl pro Spule: N , Radius: R), durch welche der Strom I gleichsinnig fließt. Die beiden Spulen haben den Abstand d voneinander (siehe Abbildung). Zeigen Sie, dass sowohl dB/dx als auch d2 B/dx2
im gemeinsamen Schwerpunkt (x = 0) der
Spulen verschwinden, wenn d = R ist. Deshalb ist das Magnetfeld von HelmholtzSpulen in der Nähe des Schwerpunktes nahezu homogen und sie werden verwendet, um
lokal homogene Magnetfelder zu erzeugen.
Aufgabe 4.8: Eine Spule mit rechteckigem Querschnitt (a = 5 cm; b = 4 cm)
und N = 100 Windungen befindet sich in einem homogenen Magnetfeld mit
B = 0, 50 T. Die Spule ist um eine zum Feld senkrechte Achse drehbar.
(a) Wie groß ist dem Betrag nach das Drehmoment, das auf die Spule ausgeübt
~ einen Winkel von 60◦
wird, wenn die Spulenebene mit dem Magnetfeld B
bildet, und ein Strom von I = 25 mA durch die Spule fließt?
(b) Wann wirkt auf die Spule das größte Drehmoment und welchen Betrag hat
es?
Lösung : (a) 1, 25 · 10−3 Nm, (b) 2, 50 · 10−3 Nm
187
~ , welches ein magnetischer Dipol mit dem
Aufgabe 4.9: Das Drehmoment M
~ erfährt, ist gegeben durch
magnetischen Moment m
~ in einem Magnetfeld B
~ =m
~ .
M
~ ×B
Zeigen Sie, ausgehend von dieser Gleichung, dass die potentielle Energie Ep
~ gegeben ist durch
eines magnetischen Moments m
~ in einem Magnetfeld B
~ .
Ep = − m
~ B
Die potentielle Energie hat hierbei den Wert Null, wenn das magnetische Mo~ gerichtet ist.
ment m
~ senkrecht zu dem Magnetfeld B
3
Aufgabe 4.10: In einem Kupferband (RH = −0, 5 · 10−10 mC , Dicke: 1, 0 mm)
fließt ein Strom senkrecht zu einem Magnetfeld B = 1, 5 T. Welche HALLSpannung liegt quer über dem Band, wenn die Stromstärke 200 A beträgt?
Lösung : 15 µV
Aufgabe 4.11: An einem n-Halbleiter (Dicke: d = 0, 25 mm) wird bei
I = 0, 1 A eine HALL-Spannung UH = −0, 8 V gemessen. Das Magnetfeld hat
den Wert 1, 0 T.
(a) Berechnen Sie die HALL-Konstante RH des Halbleiters.
(b) Wie groß ist die Anzahldichte der Elektronen?
3
Lösung : (a) RH = −2, 0 · 10−3 mC , (b) 3, 12 · 1015 cm−3
Aufgabe 4.12: (a) Zeigen Sie, dass das Verhältnis der elektrischen HALLFeldstärke EH zur elektrischen Feldstärke E, die den Strom verursacht, durch
EH
B
= |RH |
E
̺
gegeben ist, wenn der Strom senkrecht zum Magnetfeld B fließt.
(b) Berechnen Sie den Ausdruck EH /E für Kupfer (RH = −0, 5 · 10−10
̺ = 1, 7 · 10−6 Ω cm) im Falle B = 1 T.
Lösung : (b) 2, 9 · 10−3
m3
,
C
Aufgabe 4.13: Elektronen werden beim Durchlaufen einer Spannung von
1000 V beschleunigt und dann in ein homogenes Magnetfeld, das senkrecht
zur Bewegungsrichtung der Elektronen steht, eingeschossen. Wie groß ist das
Magnetfeld, wenn die Elektronen Kreisbahnen vom Radius 0, 20 m durchlaufen?
Lösung : 0, 533 mT
188
ANHANG A. AUFGABEN MIT LÖSUNGEN
Aufgabe 4.14: Dempster benutzte zur
Messung von Ionenmassen die in der Abbildung dargestellte Anordnung. Ein Ion der
Masse m und der Ladung q > 0 wird in
einer Gasentladungkammer erzeugt. Das Ion
wird beim Durchlaufen einer Spannung U beschleunigt und tritt dann in ein Magnetfeld
B ein. Dort durchläuft es einen Halbkreis und
trifft im Abstand x vom Eintrittsspalt auf eine Photoplatte. Zeigen sie, dass für die Masse
m gilt:
B2 q 2
m=
x
8U
Aufgabe 4.15: Das magnetische Feld eines Zyklotrons hat den Betrag 1, 4 T.
Die wirksame Spannung zwischen den beiden “D“s ist 0, 1 MV. Im Zyklotron
werden Protonen von kleiner kinetischer Energie auf 24 MeV beschleunigt.
(a) Wie groß ist die Zahl der Umläufe der Protonen bis zum Erreichen dieser
Energie?
(b) Welche Zeit vergeht dabei?
(c) Welchen Radius muss das Zyklotron mindestens haben?
Lösung : (a) 120, (b) 5, 62 µs, (c) 0, 51 m
Aufgaben zu Kapitel 5
Aufgabe 5.1: Eine rechteckige Leiterschleife (Widerstand R, Länge l, Breite a) wird
mit konstanter Geschwindigkeit ~v durch ein
~ gezogen (siehe Abhomogenes Magnetfeld B
bildung). Zeichnen Sie
(a) den magnetischen Fluss durch die
Leiterschleife als Funktion von x, wenn
a = 4 cm, l = 10 cm, d = 15 cm, B = 2 T
und v = 1 m/s,
(b) die induzierte Spannung Uind (x),
(c) die in Wärme umgesetzte Leistung P (x),
wenn R = 16 Ω beträgt.
Aufgabe 5.2: Eine rechteckige Spule mit N Windungen (Länge a, Breite b)
~
rotiert mit einer Frquenz f in einem homogenen Feld B.
189
(a) Zeigen Sie, dass in der Spule die induzierte Spannung
Uind = 2 π f N a b B sin(2πf t) = Û sin(2πf t)
auftritt (Prinzip des Wechselstromgenerators).
(b) Wie groß muss die Windungsfläche (A = a b) einer Spule mit 40 Windungen
sein, damit sie ein Û = 310 V bei einer Umlaufsfrequenz von 50 Hz in einem
Magnetfeld B = 0, 50 T liefert?
Lösung : A = 493 cm2
Aufgabe 5.3: Eine Spule mit der Windungsfläche A und der Windungszahl
~ gleichmäßig mit
N wird in einem homogenen, zeitkonstanten Magnetfeld B
der Drehfrequenz f gedreht. Die Drehachse steht senkrecht zum Feld. Die beiden Enden der Spule werden über einen Ohmschen Widerstand R miteinader
verbunden.
(a) Wie groß ist der Strom I(t) in der Spule?
(b) Man berechne das Drehmoment M (t), mit dem die Spule angetrieben werden muss.
(c) Wie groß ist die Antriebsleistung P (t)?
(d) Man berechne I(t), M (t) und P (t) für A = 10 cm2 , N = 10, f = 50 Hz,
B = 10 mT, R = 10 Ω.
Lösung : (a) I(t) = Iˆ sin(2πf t) mit Iˆ = 2πf N AB/R,
(b) M (t) = M̂ sin2 (2πf t) mit M̂ = 2πf N 2 A2 B 2 /R,
(c) P (t) = P̂ sin2 (2πf t) mit P̂ = (2πf N AB)2 /R,
(d) Iˆ = 3, 14 mA; M̂ = 0, 314 µN m; P̂ = 98, 7 µW
Aufgabe 5.4:
Zur Messung des Erdmagnetfeldes rotiert eine Spule
(N = 1000, A = 20 cm2 ) mit einer Drehfrequenz f = 1500 min−1 , wobei die
Drehachse senkrecht zum Magnetfeld und zur Spulenachse steht. Wie groß ist
die Feldstärke des Erdmagnetfeldes, wenn die Amplitude der in der Spule induzierten Wechselspannung 10, 0 mV beträgt?
Lösung : 3, 18 · 10−5 T
Aufgabe 5.5: Eine Induktionsspule hat 75 Windungen und eine Windungsfläche von 2, 5 cm2 . Wird die Spule aus einem homogenen Magnetfeld schnell
entfernt, wird ein Spannungsstoß von 28 µV s induziert. Die Spulenachse stand
dabei anfangs parallel zur Feldrichtung. Welchen Betrag hat das Magnetfeld?
Lösung : 1, 49 mT
Aufgabe 5.6: (a) Zeigen Sie, dass die Gegeninduktivität zweier koaxialer
Spulen
µ0 N1 N2 A2
M=
l1
190
ANHANG A. AUFGABEN MIT LÖSUNGEN
ist, wenn sich die Spule 2 (Windungszahl N2 , Querschnittsfläche A2 ) in der
Mitte einer sehr langen Spule 1 (Windungszahl N1 , Querschnittsfläche A1 mit
A1 ≥ A2 , Länge l1 ) befindet.
(b) Welche Spannung wird zwischen den Enden der kleinen Spule 2 beobachtet,
wenn die Stromstärke in der langen Spule 1 in 5 s linear von 0 auf 3 A ansteigt?
Daten der Spule 1: Länge 1 m, Durchmesser 5 cm, Windungszahl: 3500
Daten der Spule 2: Durchmesser 2 cm, Windungszahl 80
Lösung : (b) −66, 3 µV
Aufgabe 5.7: Wie groß ist die Gegeninduktivität zwischen einem unendlich langen Draht und einer rechteckigen Leiterschleife (Seitenlängen a und
b), wenn der Draht parallel zu den Seiten der Länge a verläuft und von der
nächstliegenden Seite den Abstand d hat?
Lösung : µ20πa ln(1 + db )
Aufgabe 5.8: Zeigen Sie, dass die Zeitkonstante des LR-Kreises auch als
diejenige Zeit definiert werden kann, die der Strom bis zum Erreichen seines
˙
Endwertes benötigen würde, wenn I˙ konstant bliebe und zwar I(0)
wäre.
Aufgabe 5.9: Eine Spule hat eine Länge von 20 cm und einen Durchmesser von 2 cm. Ihre Wicklung besteht aus 200 Windungen von Kupferdraht
mit einem Querschnitt vom 1 mm2 . Mit Hilfe eines Schalters wird die an
der Spule anliegende Spannung abgeschaltet und die Spule kurzgeschlossen.
Welche Zeit vergeht vom Abschaltzeitpunkt an, bis sich die Stromstärke im
Kreis auf die Hälfte verringert hat? Der spezifische Widerstand von Kupfer ist
̺Cu = 1, 7 · 10−8 Ω m.
Lösung : 0, 256 ms
Aufgabe 5.10: Durch eine Spule (N/l = 20/cm, A = 100 cm2 ) fließt der
Gleichstrom I = 2 A. Wie lang müsste die Spule sein, damit in ihr die magnetische Energie von 1 J gespeichert wird? (In der Rechnung kann die Spule als
sehr lang angenommen werden.)
Lösung : 9, 95 m
Aufgabe 5.11: Zeigen Sie, dass die Induktivität einer Ringspule mit rechteckigem Querschnitt (Höhe h, Innenradius ri , Außenradius ra und N Windungen) gegeben ist durch:
µ0 N 2 h
ra
L=
ln
.
2π
ri
(a) Leiten Sie obige Formel direkt aus der Definition der Induktivität her.
(b) Leiten Sie obige Formel außerdem her mit Hilfe des Zusammenhangs zwischen der Energie des Magnetfeldes und der Induktivität.
191
Aufgaben zu Kapitel 6
Aufgabe 6.1: Eine ebene Welle werde durch folgende Gleichung beschrieben
s(x, t) = (0, 05 cm) sin
1980 s−1 t − 6, 0 m−1 x .
Berechnen Sie
(a) die Frequenz,
(b) die Wellenlänge und
(c) die Ausbreitungsgeschwindigkeit der Welle sowie
(d) die Geschwindigkeitsamplitude und
(e) die Beschleunigungsamplitude der Teilchen in dem welleleitenden Medium!
Lösung : (a) 315 Hz, (b) 1, 05 m, (c) 330 m/s, (d) 0, 99 m/s, (e) 1960 m/s2 .
Aufgabe 6.2: Eine Welle der Frequenz 500 Hz hat eine Phasengeschwindigkeit von 350 m/s.
(a) Wie weit sind zwei Punkte voneinander entfernt, deren Phasenwinkel sich
um 600 unterscheiden?
(b) Wie groß ist die Phasenwinkeldifferenz zwischen zwei Schwingungszuständen am gleichen Ort, wenn sie einen zeitlichen Abstand von 1 ms haben?
Lösung : (a) 0, 117 m, (b) 1800 .
Aufgabe 6.3: Ein Helium-Neon Laser sendet polarisiertes, monochromatisches Licht der Wellenlänge 633 nm aus. Der Strahl habe einen konstanten, kreisförmigen Querschnitt mit dem Radius 1 mm. Die Intensität sei
gleichmäßig über dem Strahlquerschnitt verteilt. Die abgestrahlte Leistung
beträgt 3, 5 mW. Bestimmen Sie
(a) die mittlere Intensität S des Strahls,
(b) die Amplitude Ê der elektrischen Feldstärke,
(c) die Amplitude B̂ der magnetischen Induktion,
(d) die Frequenz f der elektromagnetischen Welle!
Lösung : (a) 1, 11 kW/m2 , (b) 916 V/m, (c) 3, 06 µT, (d) 4, 74 · 1014 Hz.
Aufgaben zu Kapitel 7
Aufgabe 7.1: Gegeben sei ein Glasprisma mit dem Dachwinkel γ = 600 und
dem Brechungsindex n = 1, 60. Ein Lichtstrahl falle auf die eine Seite dieses
Prismas. Für genügend große Einfallswinkel θ1 dringt der Lichtstrahl so in das
Prisma ein, daß er auf der anderen Seite wieder austritt. Geht man zu kleineren
Einfallswinkeln über, so ergibt sich irgendwann die Situation, daß das Licht
nicht mehr aus dem Prisma austritt, siehe Abbildung. Bestimmen Sie
192
ANHANG A. AUFGABEN MIT LÖSUNGEN
(a) den größten Einfallswinkel, bei dem dies der Fall ist,
(b) den Einfallswinkel, bei dem der Lichtstrahl symmetrisch (d.h. parallel zur
Basisfläche) durch das Prisma geht!
Lösung : (a) 35, 60 , (b) 53, 10 .
γ
θ1
A
A
AU
Aufgabe 7.2: Ein Beispiel für die technische Anwendung der Totalreflexion
ist die Übertragung von Daten mit Glasfasern in der optischen Nachrichtentechnik. Eine Stufenindexfaser besteht aus einem Kern (Brechungsindex nk )
und einem Mantel (Brechungsindex nm < nk ), siehe Abbildung. Das Prinzip
dieser Glasfaser beruht darauf, daß Licht, das aus dem Faserinneren auf den
Mantel fällt, dort total reflektiert wird.
nm
θmax
θg
*
nk
(a) Zeigen Sie, daß der maximale Einfallswinkel θmax , unter dem Lichtstrahlen
in die Faser eingekoppelt werden können, so daß im Innern der Faser Totalreflexion gewährleistet ist, gegeben ist durch die Beziehung
sin θmax =
1q 2
nk − n2m .
n
Hierbei bezeichnet n den Brechungsindex des Materials, aus dem die auf die
Glasfaser einfallenden Lichtstrahlen kommen.
193
(b) Welcher Wert ergibt sich für θmax , wenn n = 1, nk = 1, 474 und nm = 1, 453
betragen?
Lösung : (b) 14, 40 .
Aufgabe 7.3: Ein monochromatischer Lichtstrahl erfährt beim Durchgang
durch eine planparallele Platte eine Parallelverschiebung s, siehe Abbildung.
θ1
6
d
?
@
θ1@
@
@
@s
R
@
(a) Zeigen Sie, daß die Verschiebung s gegeben ist durch

s = d sin θ1 1 − q
cos θ1
n2
2
− sin θ1

 .
Hierbei bezeichnet n den Brechungsindex der Platte, d die Plattendicke und
θ1 den Einfallswinkel des Lichtstrahls.
(b) Welche Verschiebungen ergeben sich für rotes und violettes Licht, wenn
das Licht unter 400 auftrifft, die Platte 3 cm dick ist und die Brechungsindizes
für rotes bzw. violettes Licht 1, 6029 bzw. 1, 6542 (Flintglas) betragen?
Lösung : (a) 0, 922 cm, (b) 0, 959 cm.
Aufgabe 7.4: (a) Zeigen Sie, daß die Abbildungsgleichung für sphärische
Grenzflächen
n1 n2
n2 − n1
+
=
(A.1)
g
b
r
auch gültig bleibt, falls ein virtueller Bildpunkt entsteht! Die Bildweite b muß
in diesem Fall negativ gezählt werden.
(b) Zeigen Sie, daß Gl. (A.1) ebenfalls gültig bleibt für sphärische Grenzflächen,
deren Mittelpunkt sich links vom Scheitelpunkt befindet, also auf derselben
194
ANHANG A. AUFGABEN MIT LÖSUNGEN
Seite wie das einfallende Licht! Der Radius r der Grenzfläche muß in diesem
Fall negativ gezählt werden.
Aufgabe 7.5: Eine plankonvexe Linse mit dem Krümmungsradius r1 = 20 cm
bildet einen Gegenstand mit der Gegenstandsweite g = 70 cm in dem Abstand
b = 93, 5 cm hinter der Linse scharf ab. Wie groß ist die Brechkraft D und der
Brechungsindex nl der Linse?
Lösung : D = 2, 5 dpt, nl = 1, 5.
Aufgabe 7.6: Skizzieren Sie die verschiedenen möglichen dünnen Linsen,
die sich ergeben, wenn zwei sphärische Flächen kombiniert werden, deren
Krümmungsradien dem Betrage nach 10 cm und 15 cm sind! Welche der Linsen
sind Sammellinsen, welche Zerstreuungslinsen? Berechenen Sie für jeden Fall
die Brennweite! Der Brechnungsindex des Glases, aus dem die Linse besteht,
sei n = 1, 5.
Lösung : f = 12 cm, f = 60 cm, f = −12 cm, f = −60 cm.
Aufgabe 7.7: Eine Sammellinse der Brennweite 42 cm entwirft von einem Gegenstand ein dreifach vergrößertes, virtuelles Bild. Bestimmen Sie
Gegenstands- und Bildweite!
Lösung : 28 cm, −84 cm.
Aufgabe 7.8: Verschiebt man eine punktförmige Lichtquelle längs der optischen Achse einer Linse von 6 cm Durchmesser und 12 cm Brennweite, so
entsteht auf dem 30 cm entfernten Bildschirm zweimal ein Lichtschein von
Linsengröße. Wie weit ist die Lichtquelle in beiden Fällen von der Linse entfernt, und in welchem Falle ist der Lichtschein heller?
Lösung : 12 cm, 60 cm.
Aufgabe 7.9: Ein einfacher Fotoapparat habe eine symmetrische, dünne, bikonvexe Linse aus Glas (n = 1, 51) mit dem Krümmungsradius 76, 5 mm und
dem Durchmesser 10 mm.
(a) Um welche Strecke muß die Bildebene aus der Einstellung für Unendlich
verschoben werden, wenn ein Gegenstand in der Entfernung 2 m scharf abgebildet werden soll?
(b) Wie groß ist bei dieser Einstellung für den unendlich fernen Achsenpunkt
der Durchmesser des Unschärfekreises (Kreisförmige Fläche an Stelle des idealen Bildpunktes) in der Bildebene?
Lösung : (a) 2, 92 mm, (b) 0, 39 mm.
Aufgabe 7.10: Eine Lichtquelle befinde sich im Abstand l von einem Bildschirm und soll dort mit Hilfe einer dünnen Sammellinse (Brennweite f ) scharf
abgebildet werden.
195
(a) In welcher Entfernung vom Gegenstand muß die Sammellinse angeordnet
werden?
(b) Zeigen Sie, daß im Fall zweier Lösungen die eine aus der anderen hervorgeht, indem man Gegenstands- und Bildweite der ersten Lösung vertauscht!
(c) Welche Werte ergeben sich für die Entfernung der Sammellinse vom Gegenstand für l = 1 m undqf = 0, 21 m?
Lösung : (a) g1,2 = l/2 ± l2 /4 − lf , (c) 0, 3 m und 0, 7 m.
Aufgabe 7.11: Ein Gegenstand befindet sich 20 cm links von einer Linse mit
der Brennweite 10 cm. Eine zweite Linse mit der Brennweite 12, 5 cm befindet
sich 30 cm rechts von der ersten Linse.
(a) Betrachten Sie das von der ersten Linse entworfene Bild als Gegenstand für
die zweite Linse, und bestimmen Sie auf diese Weise Lage und relative Größe
des endgültigen Bildes! Mit relativer Größe ist die Größe des endgültigen Bildes bezogen auf den Originalgegenstand gemeint.
(b) Von welcher Art ist das endgültige Bild?
(c) Stellen Sie den Strahlengang in einer möglichst genauen Skizze dar!
Lösung : (a) Die Lage des endgültigen Bildes fällt mit der des Originalgegenstandes zusammen. Das endgültige Bild ist 5-fach vergrößert. (b) Virtuell und
umgekehrt.
Aufgabe 7.12: Zeigen Sie, daß aus der geometrischen Bildkonstruktion die
Gültigkeit der Abbildungsgleichung 1/g + 1/b = 1/f folgt! Das bedeutet: Konstruiert man das von einer dünnen Linse erzeugte Bild mit Hilfe der geometrischen Bildkonstruktion, so genügen Gegenstandsweite g, Bildweite b und
Brennweite f der Linse gerade der Abbildungsgleichung.
Aufgabe 7.13: Die Gleichung 1/g + 1/b = 1/f wird auch als GAUSSsche
Form der Abbildungsgleichung bezeichnet. Zeigen Sie: Beschreibt man die Lage des Gegenstandes durch den Abstand g ′ = g − f vom gegenstandseitigen
Brennpunkt und die Lage des Bildes durch den Abstand b′ = b − f vom bildseitigen Brennpunkt, so läßt sich die Abbildungsgleichung in der Form
g ′ b′ = f 2
schreiben! Dies ist die NEWTONsche Form der Abbildungsgleichung.
Aufgabe 7.14: Von F. W. BESSEL (1784 - 1846) stammt folgende Methode zur experimentellen Bestimmung der Brennweite f einer Sammellinse: Ein
leuchtender Gegenstand und eine Mattscheibe werden in dem festen Abstand l
(l > 4f ) aufgestellt. Verschiebt man nun die Linse auf der Geraden zwischen
dem Gegenstand und der Mattscheibe, so gibt es zwei Linsenpositionen, bei
denen eine scharfe Abbildung des Gegenstandes möglich ist. Aus dem Abstand
196
ANHANG A. AUFGABEN MIT LÖSUNGEN
d dieser beiden Linsenpositionen läßt sich die Brennweite f der Linse berechnen. Geben Sie die entsprechende Formel an!
Lösung : f = (l2 − d2 )/4l.
Aufgabe 7.15: Eine Lupe bestehe aus einer symmetrischen, bikonvexen Sammellinse. Wie groß muß der Krümmungsradius der Linsenoberflächen sein, damit die Lupe eine Standardvergrößerung von 10 hat? Der Brechungsindex des
Glases, aus dem die Lupe besteht, sei n = 1, 5.
Lösung : 2, 5 cm.
Aufgabe 7.16: Befindet sich der Gegenstand bei einer Lupe genau in der
vorderen Brennweite der Linse, so liegt das virtuelle Bild im Unendlichen. Die
Vergrößerung Γ bei dieser Betrachtungsart wird als Standardvergrößerung bezeichnet, und es gilt Γ = s0 /f . Hierbei ist s0 = 250 mm die Bezugssehweite
und f die Brennweite der Linse. Wird der Gegenstand nun näher an die Lupe
herangeführt, so rückt auch das virtuelle Bild aus dem Unendlichen näher an
die Lupe heran. Bei einer bestimmten Position des Gegenstandes liegt das virtuelle Bild gerade in der Bezugssehweite s0 vor der Linse. Unter der Annahme,
daß sich das beobachtende Auge dicht an der Lupe befindet, zeigen Sie, daß
die Vergrößerung in diesem Fall gegeben ist durch
Γ=1+
s0
.
f
Aufgabe 7.17: Ein Mikroskop hat ein Objektiv mit der Brennweite 10 mm
und ein Okular mit der Brennweite 30 mm. Die optische Tubuslänge beträgt
160 mm.
(a) In welcher Entfernung muß sich ein Gegenstand vom Objektiv befinden,
damit das durch das Okular betrachtete Bild 250 mm vom Auge (Ort des
Okulars) entfernt zu sein scheint?
(b) Wie groß ist die Vergrößerung in diesem Fall?
Lösung : (a) 10, 6 mm, (b) −152.
Aufgabe 7.18: Ein Fernrohr hat ein Objektiv mit einer Brennweite von 1, 5 m
und ein Okular mit einer Brennweite von 10 cm. Unter welchem Sehwinkel kann
man den vollständigen Mond mit diesem Fernrohr sehen, wenn man ihn mit
unbewaffnetem Auge unter einem Winkel von 31′ sieht?
Lösung : (a) 70 42′ .
197
Aufgaben zu Kapitel 8
Aufgabe 8.1: Auf einen Spalt der Breite 2 µm fällt senkrecht ein paralleles
Lichtstrahlenbündel der Wellenlänge 589 nm. Berechnen Sie, unter welchen
Winkeln zur Spaltnormalen man die Intensitätsminima beobachtet?
Lösung : ±17, 10 , ±36, 10 , ±62, 10 .
Aufgabe 8.2: Welchen Winkelabstand müssen zwei Objektpunkte haben,
damit sie mit dem Auge aufgelöst werden können? Der Pupillendurchmesser
sei d = 2 mm. Der Glaskörper des Auges hat den Brechungsindex n = 1, 34. Die
Berechnung soll für Licht der Wellenlänge λ = 550 nm durchgeführt werden.
Vergleichen Sie das Ergebnis mit dem physiologischen Grenzwinkel!
Lösung : 0, 86′ .
Aufgabe 8.3: Welchen Abstand müssen zwei Objekte auf dem Mond haben,
damit Sie mit bloßem Auge aufgelöst werden können. Der Pupillendurchmesser
sei d = 4 mm. Der Glaskörper des Auges hat den Brechungsindex n = 1, 34. Die
Berechnung soll auch hier für Licht der Wellenlänge λ = 550 nm durchgeführt
werden.
Lösung : 48 km.
Aufgabe 8.4: Ein optisches Gitter mit 1200 Strichen/mm wird mit grünem
Licht der Wellenlänge 550 nm durchstrahlt. Welche Beugungsordnungen treten
auf?
Lösung : m = 0, 1.
Aufgabe 8.5: Das Spektrum einer Kohlebogenlampe soll mit Hilfe eines Beugungsgitters auf einem Schirm abgebildet werden. Zu berücksichtigen ist der
sichtbare Bereich von 400 nm (violett) bis 750 nm (rot). Zur Verfügung steht
ein Gitter mit 1000 Strichen pro cm. Welchen Abstand vom Beugungsgitter
muß der Schirm haben, damit das Farbband im Spektrum 1. Ordnung auf eine
Breite von 10 cm auseinandergezogen wird?
Lösung : 2, 84 m.
Aufgabe 8.6: Nehmen Sie für die Wellenlängen des sichtbaren Spektrums den
Bereich von 400 nm bis 750 nm an. Berechnen Sie die Zahl der Striche pro mm,
die ein optisches Gitter haben muß, damit das gesamte sichtbare Spektrum in
erster Beugungsordnung auf einen Winkelbereich von 200 auseinandergezogen
wird!
Lösung : 859 Striche/mm.
Aufgabe 8.7: Ein optisches Gitter habe 8200 Spalte, die gleichmäßig auf insgesamt 25, 4 mm verteilt sind. Es werde senkrecht mit dem Licht einer Queck-
198
ANHANG A. AUFGABEN MIT LÖSUNGEN
silberdampflampe beleuchtet. Bei 31, 920 ist in dritter Beugungsordnung eine
intensive grüne Linie sichtbar.
(a) Welche Wellenlänge hat das grüne Licht?
(b) Welche Wellenlängendifferenz ∆λ kann man mit diesem Gitter in fünfter
Beugungsordnung bei der unter (a) berechneten Wellenlänge noch auflösen?
Lösung : (a) 546 nm, (b) 0, 0133 nm.
Aufgabe 8.8: Die beiden Natrium-D-Linien mit λ1 = 589, 5930 nm und
λ2 = 588, 9963 nm sollen mit einem Gitter getrennt werden, das 50 Striche/mm
hat. Wie breit muß dieses Gitter mindestens sein, wenn in erster Beugungsordnung gemessen werden soll?
Lösung : 20 mm.
Aufgabe 8.9: Ein paralleles Lichtstrahlenbündel fällt senkrecht auf ein optisches Gitter mit der Gitterkonstanten g. Auf einem Schirm, der die Entfernung l vom Gitter hat, findet man im Abstand e seitlich vom direkten Bild ein
Beugungsbild m-ter Ordnung.
(a) Zeigen Sie, daß die Wellenlänge des einfallenden Lichtes gegeben ist durch
λ=
g
e
√
.
m l 2 + e2
(b) Auf ein Gitter mit 540 Strichen/mm fällt Licht einer Quecksilberdampflampe in der oben beschriebenen Weise. Auf dem Schirm (l = 2, 1 m) werden
bei e = 51, 0 cm eine blaue, bei e = 64, 8 cm eine grüne und bei e = 69, 0 cm
eine gelbe Linie erster Ordnung beobachtet. Wie groß sind die Wellenlängen
dieser drei hellsten Quecksilberlinien?
Lösung : 437 nm, 546 nm, 578 nm.
Aufgabe 8.10: Ein Gitter mit 1000 Spalten/mm wird mit gelbem Natriumlicht der Wellenlänge λ = 589 nm durchstrahlt.
(a) Unter welchen Winkeln zur Gitternormalen liegen die Beugungsmaxima
erster Ordnung?
(b) Das Gitter wird nun um β = 100 gedreht, so daß es von dem einfallenden
Licht schräg durchstrahlt wird. Unter welchen Winkeln zur Gitternormalen
liegen jetzt die Beugungsmaxima erster Ordnung?
Lösung : (a) θmax,1 = +36, 10 , θmax,−1 = −36, 10 , (b) θmax,1 = +49, 70 ,
θmax,−1 = −24, 50 .
Anhang B
Lineare Differentialgleichungen
In diesem Abschnitt sind einige Begriffe und Sätze aus dem Gebiet der linearen Differentialgleichungen zusammengestellt, die unter anderem bei der
Beschreibung von Schwingungen immer wieder benötigt werden.
Definition 1 Eine Gleichung, in der eine unbekannte Funktion y(x) und ihre
Ableitungen bis zur n-ten Ordnung auftreten, heißt eine gewöhnliche Differentialgleichung (DGL) n-ter Ordnung.
Ein Beispiel für eine gewöhnliche Differentialgleichung 1. Ordnung ist die
Gleichung
y ′ + y = 2x .
(B.1)
Eine Differentialgleichung kann als Bestimmungsgleichung für eine unbekannte
Funktion aufgefaßt werden. Eine Funktion y(x) ist eine Lösung der Differentialgleichung, wenn sie mitsamt ihren Ableitungen die Differentialgleichung
identisch erfüllt. Für die Gl. (B.1) läßt sich leicht nachprüfen, daß die Funktionen
y(x) = c e−x + 2x − 2
(c ∈ IR)
Lösungen sind.
Bei der mathematischen Beschreibung von Schwingungen ist der folgende
Typ von Differentialgleichungen von großer Bedeutung:
Definition 2 Eine Differentialgleichung vom Typ
y ′′ + ay ′ + by = g(x)
(a, b ∈ IR)
heißt eine lineare Differentialgleichung 2. Ordnung mit konstanten Koeffizienten.
199
200
ANHANG B. LINEARE DIFFERENTIALGLEICHUNGEN
Die Funktion g(x) wird als Störfunktion bezeichnet. Fehlt diese, d.h. ist
g(x) ≡ 0, so heißt die lineare Differentialgleichung homogen, sonst inhomogen. Der folgende Satz macht eine Aussage über die Lösungen von homogenen
Differentialgleichungen 2. Ordnung:
Satz 1 Für die Lösungen einer homogenen linearen Differentialgleichung
2. Ordnung mit konstanten Koeffizienten vom Typ
y ′′ + ay ′ + by = 0
gilt:
1. Ist y1 (x) eine Lösung der Differentialgleichung, so ist auch die mit einer
beliebigen Konstanten c multiplizierte Funktion
y(x) = cy1 (x)
(c ∈ IR)
eine Lösung der Differentialgleichung.
2. Sind y1 (x) und y2 (x) zwei Lösungen der Differentialgleichung, so ist auch
die aus ihnen gebildete Linearkombination
y(x) = c1 y1 (x) + c2 y2 (x)
(c1 , c2 ∈ IR)
eine Lösung der Differentialgleichung .
Um eine Aussage über die Menge aller Lösungen einer homogenen linearen Differentialgleichung 2. Ordnung mit konstanten Koeffizienten machen zu
können, benötigen wir folgende Definition:
Definition 3 Zwei Lösungen y1 (x) und y2 (x) heißen linear unabhängig, wenn
die für alle x gültige Gleichung
c1 y1 (x) + c2 y2 (x) = 0
nur trivial, d.h. für c1 = 0, c2 = 0 lösbar ist.
Ob zwei Lösungen linear unabhängig sind, läßt sich mit Hilfe der sogenannten WRONSKI-Determinate nachprüfen. Sie ist definiert durch
y (x)
W [y1 , y2 ] := 1′
y1 (x)
y2 (x)
y2′ (x)
.
201
Ist die WRONSKI-Determinante an einer Stelle x = x0 von Null verschieden,
so sind die Lösungen y1 (x) und y2 (x) linear unabhängig. Verschwindet sie
dagegen an einer Stelle x = x0 , so sind die Lösungen y1 (x) und y2 (x) linear
abhängig.
Die gesamte Lösungsmenge einer homogenen linearen Differentialgleichung
2. Ordnung mit konstanten Koeffizienten wird nun durch folgenden Satz beschrieben:
Satz 2 Die allgemeine Lösung y(x) einer homogenen linearen Differentialgleichung 2. Ordnung mit konstanten Koeffizienten vom Typ
y ′′ + ay ′ + by = 0
(B.2)
ist als Linearkombination zweier linear unabhängiger Lösungen (Basislösungen) y1 (x) und y2 (x) darstellbar, in Zeichen
y(x) = c1 y1 (x) + c2 y2 (x)
(c1 , c2 ∈ IR) .
Die Aussage dieses Satzes läßt sich auch so formulieren: Die Lösungen der
Gl. (B.2) bilden einen zweidimensionalen Vektorraum. Die der allgemeinen
Lösung zugrunde liegenden Basislösungen y1 (x) und y2 (x) bilden ein Fundamentalsystem der Differentialgleichung. Die Konstanten c1 , c2 lassen sich eindeutig bestimmen aus den Anfangsbedingungen y(x0 ) = y0 und y ′ (x0 ) = y1 .
Die Lösungsmenge einer inhomogenen linearen Differentialgleichung 2. Ordnung mit konstanten Koeffizienten wird durch folgenden Satz beschrieben:
Satz 3 Die allgemeine Lösung y(x) einer inhomogenen linearen Differentialgleichung 2. Ordnung mit konstanten Koeffizienten vom Typ
y ′′ + ay ′ + by = g(x)
ist als Summe aus der allgemeinen Lösung yh (x) der zugehörigen homogenen
linearen Differentialgleichung
y ′′ + ay ′ + by = 0
und einer beliebigen speziellen (partikulären) Lösung yp (x) der inhomogenen
linearen Differentialgleichung darstellbar, in Zeichen
y(x) = yh (x) + yp (x) .
202
ANHANG B. LINEARE DIFFERENTIALGLEICHUNGEN
Anhang C
Literaturverzeichnis
H. Lindner Physik für Ingenieure. Fachbuchverlag, Leipzig Köln.
P. Dobrinski, G. Krakau, A. Vogel Physik für Ingenieure. Teubner Verlag, Stuttgart.
Paul A. Tipler Physik. Spektrum Akademischer Verlag, Heidelberg.
F. J. Keller, W. E. Gettys, M. J. Skove Physics.
York.
McGraw-Hill,
New
C. Gerthsen, H. O. Kneser, H. Vogel Physik. Springer Verlag, Berlin.
F. Kuypers Physik, Band 2, Elektrizität, Optik und Wellen. Wiley-VCH Verlag, Weinheim.
W. Demtröder Experimentalphysik, Band 2, Elektrizität und Optik. Springer Verlag, Berlin.
Edward M. Purcell Berkeley Physik Kurs, Band 2, Elektrizität und Magnetismus. Vieweg Verlag, Braunschweig.
E. Hecht Optik. Addison-Wesley Verlag, Bonn.
H. Kuchling Taschenbuch der Physik. Fachbuchverlag Leipzig Köln.
203
204
ANHANG C. LITERATURVERZEICHNIS
Anhang D
Physikalische Konstanten
Lichtgeschwindigkeit
Gravitationskonstante
BOLTZMANN-Konstante
c
G
k
AVOGADRO-Konstante
Universelle Gaskonstante
Atomare Masseneinheit
Magnetische Feldkonstante
Elektrische Feldkonstante
PLANCK-Konstante
NA
R
u
µ0
ε0
h
Elementarladung
Ruhemasse des Elektrons
Ruhemasse des Protons
Ruhemasse des Neutrons
BOHRscher Radius
BOHRsches Magneton
RYDBERG-Konstante
STEFAN-BOLTZMANN-Konst.
e
me
mp
mn
rB
µB
R∞
σ
299 792 458 m s−1
6, 67259(85) · 10−11 N m2 kg−2
1, 380658(12) · 10−23 J K−1
8, 617385(73) · 10−5 eV K−1
6, 0221367(36) · 1023 mol−1
8, 314510(70) J mol−1 K−1
1, 6605402(10) · 10−27 kg
4π · 10−7 H m−1
8, 854187817 . . . · 10−12 F m−1
6, 6260755(40) · 10−34 J s
4, 1356692(12) · 10−15 eV s
1, 60217733(49) · 10−19 C
9, 1093897(54) · 10−31 kg
1, 6726231(10) · 10−27 kg
1, 6749286(10) · 10−27 kg
0, 529177249(24) · 10−10 m
9, 2740154(31) · 10−24 J T−1
1, 0973731534(13) · 107 m−1
5, 67051(19) · 10−8 W m−2 K−4
Die in den Klammern angegebenen Ziffern bedeuten die Standardabweichung (mittlerer quadratischer Fehler), angegeben in Ziffern der letzten Stelle,
Beispiel: 6, 67259(85) = 6, 67259 ± 0, 00085.
205
206
ANHANG D. PHYSIKALISCHE KONSTANTEN
Anhang E
Das Griechische Alphabet
Für zahlreiche physikalische Größen werden Buchstaben des griechischen Alphabets verwendet. Es ist deshalb nachfolgend aufgeführt.
Name
groß
Alpha
A
Beta
B
Gamma
Γ
Delta
∆
Epsilon
E
Zeta
Z
Eta
H
Theta
Θ
Iota
I
Kappa
K
Lambda
Λ
Mü
M
klein
α
β
γ
δ
ǫ, ε
ζ
η
θ, ϑ
ι
κ
λ
µ
Name
Nü
Xi
Omikron
Pi
Rho
Sigma
Tau
Ypsilon
Phi
Chi
Psi
Omega
207
groß
N
Ξ
O
Π
P
Σ
T
Υ
Φ
X
Ψ
Ω
klein
ν
ξ
o
π
ρ, ̺
σ
τ
υ
φ, ϕ
χ
ψ
ω