Woche 4: Gemeinsame Verteilungen
Werbung
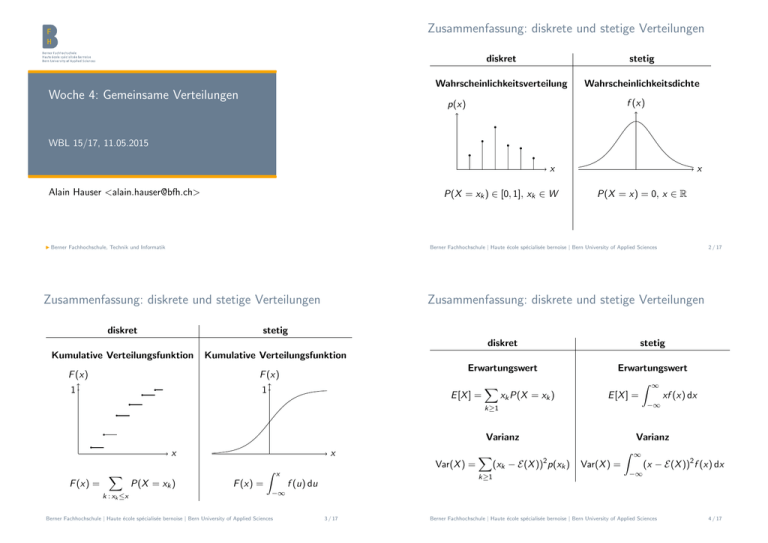
Zusammenfassung: diskrete und stetige Verteilungen Woche 4: Gemeinsame Verteilungen diskret stetig Wahrscheinlichkeitsverteilung Wahrscheinlichkeitsdichte f (x) p(x) WBL 15/17, 11.05.2015 x Alain Hauser <[email protected]> P(X = xk ) ∈ [0, 1], xk ∈ W x P(X = x) = 0, x ∈ R Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences Berner Fachhochschule, Technik und Informatik Zusammenfassung: diskrete und stetige Verteilungen Zusammenfassung: diskrete und stetige Verteilungen diskret stetig Kumulative Verteilungsfunktion Kumulative Verteilungsfunktion F (x) F (x) 1 1 diskret stetig Erwartungswert Erwartungswert Z ∞ E [X ] = xf (x) dx E [X ] = X xk P(X = xk ) −∞ k≥1 Varianz x F (x) = X k : xk ≤x x Z P(X = xk ) x F (x) = 2 / 17 X Var(X ) = (xk − E(X ))2 p(xk ) k≥1 f (u) du Varianz Z ∞ Var(X ) = (x − E(X ))2 f (x) dx −∞ −∞ Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 3 / 17 Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 4 / 17 Lernziele Sie können. . . Teil III Gemeinsame Verteilungen Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 5 / 17 Gemeinsame Verteilung I . . . die gemeinsame Verteilung von zwei Zufallsvariablen angeben. I . . . aus der gemeinsamen Verteilung zweier Zufallsvariablen deren Randverteilungen berechnen. I . . . feststellen, ob zwei Zufallsvariablen unabhängig sind. I . . . die Kovarianz und den Korrelationskoeffizient zweier Zufallsvariablen berechnen und interpretieren. I . . . Erwartungswert und Varianz einer Linearkombination zweier Zufallsvariablen berechnen. Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 6 / 17 Diskrete gemeinsame Verteilungen Situation: I X : diskrete Zufallsvariable mit Werten in WX = {x1 , x2 , x3 , . . .} I Y : diskrete Zufallsvariable mit Werten in WY = {y1 , y2 , y3 , . . .} Bisher haben wir immer die Verteilung einer einzelnen Zufallsvariablen betrachtet. Definition I In der Praxis betrachten wir natürlich oft mehrere Grössen gleichzeitig Die gemeinsame kumulative Verteilungsfunktion von X und Y ist die Funktion I Zwei (oder mehr) Zufallsvariablen lassen sich mit Hilfe ihrer “gemeinsamen Verteilung” beschreiben I FX ,Y (x, y ) := P(X ≤ x, Y ≤ y ) . Die gemeinsame Wahrscheinlichkeitsverteilung von X und Y bezeichnet die Wahrscheinlichkeiten P(X = x, Y = y ), x ∈ WX , y ∈ WY . Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 7 / 17 Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 8 / 17 Beispiel: gemeinsame Wahrscheinlichkeitsverteilung Randverteilungen X und Y seien zwei diskrete Zufallsvariablen mit Wertebereichen WX und WY . I Eine gemeinsame Wahrscheinlichkeitsverteilung zweier Zufallsvariablen kann als Tabelle angegeben werden I Beispiel: parallelisierter Algorithmus läuft auf 2 Prozessorkernen Definition (Randverteilung) I Zufallsvariablen X und Y : diskretisierte Last der beiden Kerne (1 = tiefe Last, 2 = mittlere Last, 3 = hohe Last) Die Verteilung von X allein heisst Randverteilung; sie wird berechnet als X P(X = x) = P(X = x, Y = y ) für beliebige x ∈ WX . X /Y 1 2 3 1 0.31 0.11 0.04 2 0.08 0.18 0.09 3 0.02 0.06 0.11 y ∈WY Definition Wie kann man die Verteilung in Worte fassen? Ist die Auslastung der Kerne z.B. gleichmässig? X und Y sind unabhängig wenn P(X = x, Y = y ) = P(X = x) · P(Y = y ) gilt für alle Werte x und y , die X und Y annehmen können. Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 9 / 17 Bedingte Verteilungen Stetige gemeinsame Verteilungen I I X und Y seien zwei diskrete Zufallsvariablen mit gemeinsamer Verteilung P(X = x, Y = y ). Definition (Bedingte Wahrscheinlichkeitsverteilung) Sind X und Y zwei stetige Zufallsvariablen, besitzen sie eine gemeinsame Wahrscheinlichkeitsdichte fX ,Y (x, y ). Die Wahrscheinlichkeit, dass X in einem Intervall [a, b] und Y in einem Intervall [c, d] liegt, berechnet sich gemäss Z bZ d P(a ≤ X ≤ b, c ≤ Y ≤ d) = fX ,Y (x, y ) dy dx a I Die bedingte Wahrscheinlichkeitsverteilung von X gegeben Y = y ist P(X = x, Y = y ) P(X = x | Y = y ) = P(Y = y ) c Die Randdichte von X erhält man durch Ausintegrieren über Y: Z ∞ fX (x) = fX ,Y (x, y ) dy . −∞ I Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 10 / 17 11 / 17 Wie bei diskreten Verteilungen kann man die bedingte Verteilung von X gegeben Y definieren; sie hat die Dichte fX ,Y (x, y ) fX |Y =y (x) = fY (y ) Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 12 / 17 Kontur-Plot I X und Y seien zwei (diskrete oder stetige) Zufallsvariablen. Eine gemeinsame Dichte lässt sich mit einem Kontur-Plot visualisieren: eine Art “Plot von Höhenkurven” der Dichte “Höhenkurve” hier: Linie aller Punkte, wo die gemeinsame Dichte einen bestimmten Wert hat Definition Die Kovarianz von X und Y ist definiert als h i Cov(X , Y ) := E X − E(X ) Y − E(Y ) . 0.02 2 I Kovarianz und Korrelationskoeffizient Cov(X , Y ) Ihr Korrelationskoeffizient ist ρXY = p . Var(X ) Var(Y ) 1 0.06 0.1 y 0 4 0.1 6 0.1 −1 0.1 Eigenschaften: I Falls X und Y unabhängig sind, ist Cov(X , Y ) = 0 und ρXY = 0 (die andere Richtung ist i.A. falsch!!) I −1 ≤ ρXY ≤ 1 I ρXY = ±1 falls Y deterministisch linear von X abhängt (Beispiel: X = Temperatur in ◦ C , Y = Temperatur in ◦ F ) 2 −2 0.08 0.04 −2 −1 0 x 1 2 Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 13 / 17 Korrelation: Beispiele ρXY = 0 2 3 −3 0. 2 3 8 1 0 Abhängigkeit impliziert Kausalität −2 −3 −1 0 1 2 3 2 3 ρXY = 0.95 15 −3 −1 0.1 15 0. 5 0.0 −2 5 0.0 −2 −2 3 I 2 1 0 1 0 0.1 08 1 2 0.1 0. 0.04 0 1 2 2 0.02 −1 0 ρXY = 0.9 6 0.0 −3 −1 Unkorreliertheit impliziert Unabhängigkeit 0.04 1 1 ρXY = 0.7 I 0 0 0.02 −2 −2 −1 6 0.0 0.0 08 0.04 Verbreitete Fehlvorstellungen: 0.02 2 0. 0.1 0.06 1 0.04 0 0 1 06 −3 ρXY = 0.5 2 2 0. 14 / 17 Unabhängigkeit und Kausalität ρXY = −0.5 0.02 Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 0 1 2 3 −3 −1 0 1 (Quelle: https://xkcd.com/552/) Mehr dazu: Kapitel “deskriptive Statistik”, nächste Vorlesung. Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 15 / 17 Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 16 / 17 Rechenregeln für Erwartungswert und Varianz X und Y seien (diskrete oder stetige) Zufallsvariablen, a ∈ R eine reelle Zahl. I E(X + Y ) = E(X ) + E(Y ) I Falls X und Y unabhängig sind, gilt E(X · Y ) = E(X ) · E(Y ) I E(a · X ) = a · E(X ) I Var(X + Y ) = Var(X ) + Var(Y ) + 2 Cov(X , Y ) I Folge: falls X und Y unabhängig sind, gilt Var(X + Y ) = Var(X ) + Var(Y ) I Var(a · X ) = a2 · Var(X ) Berner Fachhochschule | Haute école spécialisée bernoise | Bern University of Applied Sciences 17 / 17