Übungsblatt 4 (08.06.2012) - Lehrstuhl für Optik, Uni Erlangen

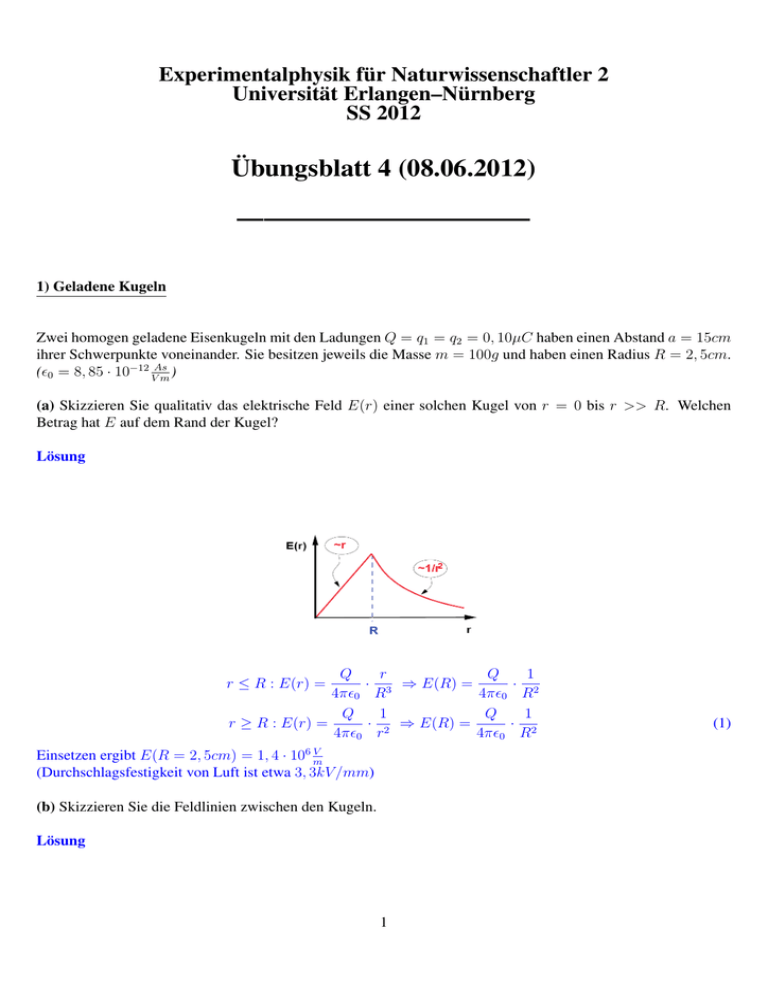
Experimentalphysik für Naturwissenschaftler 2
Universität Erlangen–Nürnberg
SS 2012
Übungsblatt 4 (08.06.2012)
———————————
1) Geladene Kugeln
Zwei homogen geladene Eisenkugeln mit den Ladungen Q = q1 = q2 = 0, 10µC haben einen Abstand a = 15cm
ihrer Schwerpunkte voneinander. Sie besitzen jeweils die Masse m = 100g und haben einen Radius R = 2, 5cm.
(0 = 8, 85 · 10−12 VAsm )
(a) Skizzieren Sie qualitativ das elektrische Feld E(r) einer solchen Kugel von r = 0 bis r >> R. Welchen
Betrag hat E auf dem Rand der Kugel?
Lösung
r
Q
1
Q
· 3 ⇒ E(R) =
· 2
4π0 R
4π0 R
Q
1
1
Q
r ≥ R : E(r) =
· 2 ⇒ E(R) =
· 2
4π0 r
4π0 R
r ≤ R : E(r) =
V
Einsetzen ergibt E(R = 2, 5cm) = 1, 4 · 106 m
(Durchschlagsfestigkeit von Luft ist etwa 3, 3kV /mm)
(b) Skizzieren Sie die Feldlinien zwischen den Kugeln.
Lösung
1
(1)
Jede Ladung erzeugt (jedenfalls außerhalb der geladenen Kugel) ein radialsymmetrisches Feld wie eine Punktladung. Feldstärkevektoren müssen vektoriell addiert werden. Dadurch kann es z.B. auf der Symmetrieachse
zwischen den Ladungen keine horizontale Komponente des elektrischen Feldes geben. Links von der linken
Ladung bzw. rechts von der rechten Ladung ist der Einfluss der zweiten Ladung wegen des großen Abstandes zur
jeweils anderen Ladung sehr gering, so dass dort näherungsweise das Feld einer einzelnen Punktladung entsteht.
(c) Welche Kraft wirkt zwischen den Kugeln und wie ist sie gerichtet?
Lösung
Die Kugeln sind homogen geladen, daher Kraft zwischen zwei Punktladungen:
1
Q2
· 2 = 4, 0mN
4π0 a
Kugeln stoßen sich aufgrund des gleichen Vorzeichens der Ladungen ab.
F =
(2)
(d) Die Kugeln werden nun an masselosen Fäden der Länge l = 1m am gleichen Punkt aufgehängt und stoßen
sich aufgrund der positiven Ladungen ab. Welchen Abstand nehmen die Kugelschwerpunkte zueinander an?
(Benutzen Sie die Kleinwinkelnäherung, also tan x ≈ sin x)
≈
2
Lösung
Die Kugeln können als Punktladungen betrachtet werden, allerdings muss bei folgender Rechnung der Radius
R der Kugeln berücksichtigt werden, um die korrekte Position der effektiv wirkenden Punktladung wiederzugeben.
Auf jede der Kugeln wirkt die Gravitationskraft senkrecht nach unten und die abstoßende Coulomb-Kraft horizontal. Diese Kräfte addieren sich zu einer Gesamtkraft, die längs des gestrafften Fadens wirkt und einen Winkel
α mit der Vertikalen einnimmt.
Der Auslenkungswinkel α stellt sich also so ein, dass der Winkel des Fadens mit der Vertikalen, der vom
Abstand d der Kugeln abhängt, gleich α ist.
d/2
und tan α = FFCg
Es gilt: sin α = l+R
Kleinwinkelnäherung: tan α ≈ sin α
Q2
1
d
· 2
≈
4π0 d mg
2(l + R)
2
1/3
2Q (l + R)
d=
= 5, 7cm
4π0 mg
(3)
(4)
2) Elektrische Feldlinien
Welche der unten gezeigten Feldlinienbilder sind für statische elektrische Felder verboten, welche sind erlaubt?
Aus welchem Grund sind sie verboten bzw. erlaubt?
3
Lösung
(a) Verboten, da es keine geschlossenen elektrischen Feldlinien gibt (im statischen Fall) und die Felder immer
senkrecht auf Metalloberflächen steht.
(b) Erlaubt. Coulombfeld einer Punktladung.
(c) Verboten, da sich Feldlinien nicht kreuzen. Zwei sich kreuzende Feldlinien würden bedeuten, dass es an einer
Stelle zwei unterschiedliche Richtungen des elektrischen Feldes gibt. Das resultierende Feld einer
Ladungsverteilung ergibt sich jedoch als vektorielle Summe der Coulomb-Felder aller Punktladungen und hat
damit eine eindeutige Richtung an jeder Stelle!
(d) Verboten. Feldlinien zeigen nicht auf positive Ladungen, außerdem sind die Feldlinien geschlossen
(e) Erlaubt. Dipol Feld.
(f) Erlaubt. Feld in einem Plattenkondensator
3) Widerstände
Ein Widerstandsnetzwerk besteht aus 12 wie im nebenstehenden Bild angeordneten Widerständen. Der Wert jedes
Widerstandes beträgt 2Ω.
An die Punkte A und B wird eine Spannung von 12V angelegt.
a) Berechnen Sie den Gesamtwiderstand der Anordnung, den Gesamtstrom
sowie die Ströme durch die einzelnen Widerstände. Nutzen Sie hierfür die
Symmetrie der Anordnung (Überlegen Sie qualitativ, welche Ströme am
Punkt C fließen).
b) Welche Leistung wird in den Widerständen umgesetzt?
c) Die Punkte A und C werden nun leitend verbunden. Berechnen Sie den
Gesamtstrom sowie den Strom durch die am Punkt B angrenzenden Widerstände. Würden Widerstände, die eine maximale Leistung von 25W aushalten, hier noch einsetzbar sein?
4
Lösung a) Aus Symmetriegründen fließt durch C von oben nach unten und von
links nach rechts kein Strom, da das Widerstandsnetzwerk auch wie in nebenstehender Abbildung interpretiert werden kann.
Der Widerstand der "inneren" Parallelschaltung eines Zweiges: Ri =
1 −1
1
+ 2R
=R
2R
Also hat ein Zweig Rz = 3 ∗ R und das gesamte Netzwerk
Rz
= 1.5R = 3Ω
2
1
Rges
= 2 ∗ R1z ⇒ Rges =
Es fließt also ein Strom von Iges = 4A.
Durch die beiden Zweige also jeweils 2A und durch die Widerstände der inneren Paralellschaltungen jeweils 1A, da sich der Strom zu jeweils gleichen Teilen
aufteilt.
b) Mit P = I 2 R ergeben sich Leistungen von P (2A) = 8W und P (1A) = 2W .
c) Die Schaltung kann nun wie rechts dargestellt gezeichnet werden. Innerer
Teil eines Zweiges(rot): Ri = R2 + 2R = 5Ω, gesamter Zweig Rz =
−1
1
1
+
+ R = 3, 43Ω und damit der gesamte Widerstand Rges = R2z =
Ri
R
1, 71Ω
Damit ergibt sich jetzt ein Gesamtstrom von Iges = 7, 0A, wovon jeweils die
Hälfte durch die untersten beiden Widerstände fließt, womit sich ein Leistungsabfall
von P = 24, 5W ergibt und der Widerstand damit gerade noch verwendbar ist.
5