Grundeigenschaften neuronaler Netze Neuronen: Aufbau und

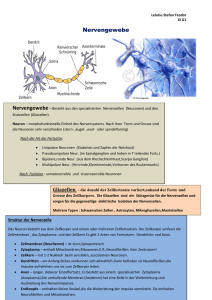
Grundeigenschaften neuronaler Netze § 1
Neuronale Netze
NEURONALE NETZE
Grundeigenschaften neuronaler Netze
Aufgabe neuronaler Netze ist es, in mehr oder weniger grober Form die Eigenschaften realer Nervensysteme
nachzubilden.
Einige elementare Erkenntnisse sollen den Unterschied zwischen realen Nervensystemen und einem
sequentiellen Computer verdeutlichen:
Reale Nervensysteme arbeiten mit relativ langsamen Elementen, den Neuronen. Ihre Verarbeitungszeiten
liegen im Bereich von 1 - 100 ms. Trotzdem sind sie zu unglaublichen Leistungen fähig. Beispielsweise ist das
Auge-Hirn-System des Menschen in der Lage, in Echtzeit (50 - 100 ms) eine Datenreduktion von ca. 1 Gbit/s
(das ist etwa die Eingangs-Datenrate an der Netzhaut des Auges) in einem mehrstufigen Prozess auf einige 10
Bit/s vorzunehmen, die wir mehr oder weniger bewusst wahrnehmen.
Reale Nervensysteme können komplexe, stark gestörte Muster in Echtzeit erkennen und verfügen über eine
erstaunliche Lern- und Adaptionsfähigkeit.
Außerdem ist unser Nervensystem ein hochgradig paralleles System (im Gegensatz zu den meisten heutigen
Computersystemen, die im wesentlichen sequentiell arbeiten) mit einem ungeheuren Vernetzungsgrad. Das
menschliche Gehirn besteht aus etwa 1010 bis 1011 Neuronen. Jedes von ihnen verfügt über bis zu 100
Verbindungen zu anderen Neuronen (Synapsen), sodass daraus eine Gesamtzahl von Verbindungen in der
Größenordnung von bis zu 1015 resultiert. Daraus ergibt sich eine Verarbeitungsleistung, die durch alle
Supercomputer zusammengenommen nicht im entferntesten erreicht werden kann.
Die Daten in den meisten heutigen Computern sind an Stellen abgelegt, deren Adressen in keinerlei Beziehung
zum Inhalt stehen. Bei Abruf eines Datums muß eine exakte Adresse angegeben werden, sonst ist kein
Zugang möglich. Diese Zugriffsart ist von Nachteil, wenn ein Teil des gesuchten Inhalts schon bekannt ist,
der Rest aber vervollständigt werden soll. Besser geeignet für solche Anforderungen wäre die assoziative
Speicherung. Dabei geschieht der Datenabruf auf der Basis der Ähnlichkeit zwischen einer Vorgabe und den
gespeicherten Inhalten. Mit relativ geringem Verarbeitungsaufwand wird dasjenige Datum geliefert, das der
vorliegenden Spezifikation am ähnlichsten ist.
Weiters sind herkömmliche Computer wenig fehlertolerant. Bei fehlenden Daten kann evtl. noch Vorsorge
getroffen werden, ein fehlender Programmteil jedoch hat katastrophale Auswirkungen. Auch sind Programme
i. a. sehr unflexibel, d. h. die Modifikation eines Programmes zur Laufzeit ist unüblich bzw. nur im Rahmen einer
vorhersehbaren Anpassung möglich!
Neuronen: Aufbau und Modellbildung
Ein Nervensystem besteht aus einer Vielzahl von miteinander kommunizierenden Nervenzellen (Neuronen).
Jedes Neuron besteht aus einem Zellkörper (von seiner Umgebung durch die Zellmembran abgetrennt) mit
einem Zellkern und einer großen Zahl von Fortsätzen.
Dabei unterscheidet man zwei Typen: Die vielfach
Neuron
verzweigten Auswüchse heißen Dendriten. Daneben
besitzt jedes Neuron genau eine (bis zu etwa 1m Axon
[Rückenmark[) lange Nervenfaser, die Axon genannt wird
und die Hauptverbindung zu anderen Neuronen darstellt.
Das Axon verzweigt sich an seinem Ende, wobei jede
Verzweigung durch eine Synapse abgeschlossen wird.
Diese ist - nur durch den schmalen synaptischen Spalt
Synapse
getrennt - mit dem Zellkörper oder einem Dendriten eines
anderen Neurons verbunden. So entsteht eine
hochgradige Vernetzung der einzelnen Nervenzellen.
Die Vorgänge innerhalb eines Neurons sind
Dendrit
elektrochemischer Natur. Wird ein Neuron über einen
bestimmten Schwellwert hinaus erregt, ändern sich fast
Robert Salvador
2001
Neuronen: Aufbau und Modellbildung § 2
Neuronale Netze
schlagartig die Potentialverhältnisse an seiner Membran: das Neuron feuert. Dieses sogenannte
Aktivierungspotential hält jedoch nur etwa 1 ms an bevor das Neuron in den Ruhezustand zurückkehrt. Das
Aktivierungspotential wird über das Axon an die mit ihm verbundenen Neuronen weitergeleitet. An den
Synapsen angelangt, regt es diese zur Erzeugung bestimmter chemischer Substanzen (Neurotransmitter) an,
die über den synaptischen Spalt gelangen können und ihrerseits das nachfolgende Neuron beeinflussen
(Anregung oder Hemmung).
Eine ganz wesentliche Eigenschaft biologischer Neuronennetze liegt in der Tatsache, dass sich die
synaptischen Verbindungen mit der Zeit ändern können. Synapsen können wachsen, schrumpfen oder auch
gänzlich verschwinden. Durch Ausbildung neuer Axon-Verzweigungen können neue Verbindungen
hergestellt werden. Diese Änderungen sind die Grundlage der Lernfähigkeit neuronaler Netze.
Von systemtheoretischer Seite her betrachtet können wir also festhalten:
• Ein Neuron besitzt eine Anzahl von Eingängen (die synaptischen Verbindungen) und einen Ausgang (das
Axon)
• Ein Neuron kann im inaktiven oder im aktiven Zustand sein
• Der Ausgang eines Neuron führt i. a. zu vielen Eingängen anderer Neuronen. Der Zustand eines Neurons
ist lediglich von seinen Eingangswerten abhängig - die einzelnen Neuronen arbeiten unabhängig
voneinander
• Ein Neuron wird aktiv, wenn seine Eingänge über ein bestimmtes Maß hinaus angeregt werden
• Die einzelnen Synapsen einer Nervenzelle tragen mit unterschiedlicher Intensität (Synapsenstärke) zur
Erregung bei. Die Eingänge werden also mit bestimmten Gewichten wi versehen; daraus wird dann ein
effektiver Eingangswert ∑„berechnet“ (gewichtete Mittelwertbildung)
• Die Aktivität eines Neurons ergibt sich aus dem effektiven Eingangswert über die sogenannte
Aktivierungsfunktion akt
Die modellmäßige Umsetzung dieser Eigenschaften kann zur folgenden Darstellung eines Neurons führen:
x1
w1
x2
w2
∑
...
xn
akt
y
wn
Für das „Ausgangssignal“ des Neurons ergibt sich damit:
n
y = akt( Σ) = akt( ∑ w k x k ) .
k =1
Die Aktivierungsfunktion ist häufig durch die Einheits-Sprungfunktion oder durch Funktionen mit etwa
folgendem Verlauf gegeben:
1
akt(Σ)
0.5
Σ→
Das bedeutet im wesentlichen, dass
das Neuron bei Überschreiten eines
gewissen Mindestreizes aktiv wird.
Im vorliegenden Mathcad-Dokument wurde eine differenzierbare Aktivierungsfunktion, nämlich
Robert Salvador
2001
Aufbau des verwendeten künstlichen neuronalen Netzes § 3
Neuronale Netze
akt( x ) =
1
1+e
−x
gewählt. Sie hat die für das Training des neuronalen Netzes angenehme Eigenschaft
d
dx
akt( x ) = akt( x) ⋅ (1 − akt( x ))
Aufbau des verwendeten künstlichen neuronalen Netzes
Ein künstliches Neuron kann nach den bisherigen Ausführungen als nichtlineares (Aktivierungsfunktion)
Übertragungssystem interpretiert werden. Dabei ist die Nichtlinearität von entscheidender Bedeutung! Durch
Zusammenschalten solcher Systeme entsteht ein neuronales Netz, das ein komplexes Übertragungssystem mit
Ein- und Ausgängen darstellt. Normalerweise sind alle Neuronen im Netz vom gleichen Typ, sodass sich ihr
Übertragungsverhalten nur durch die speziellen Gewichtungen unterscheidet. Unser Netz ist in drei Schichten
aufgebaut, wobei jede Schicht aus mehreren Neuronen besteht. Man spricht von der Eingangsschicht (input
layer – sie nimmt die Reize der Außenwelt auf), der Ausgangsschicht (output layer – sie liefert die
entsprechende Reaktion) und der dazwischen liegenden versteckten Schicht (hidden layer – sie ist
mitverantwortlich für den notwendigen Vernetzungsgrad ):
z0
w0,0
w0,1
x0
v0,0
z1
v0,1
y0
.
.
.
yp-1
z2
x1
.
.
.
xn-1
.
.
.
zl-1
wn-1,l-1
vl-1,p-1
Ausgangsschich
t
(output layer)
Eingangsschicht
(input layer)
Versteckte Schicht
(hidden layer)
Lernen im neuronalen Netz
Die Aufgabe besteht darin, ein neuronales Netz für die Mustererkennung bzw. –unterscheidung einzusetzen.
Konkret soll das Netz in der Lage sein, Großbuchstaben richtig zu erkennen (auch dann, wenn diese in nicht
ganz idealer Form vorliegen).
Die Muster werden als 7×5-Matrizen mit den Elementen 0 oder 1 definiert, z. B.:
Jedem Matrixelement (Pixel) entspricht ein Eingangsneuron (daher 35 Eingangsneuronen), jedem Buchstaben
ein Ausgangsneuron (→ 26 Ausgangsneuronen). Die versteckte Schicht enthält 30 Neuronen.
Robert Salvador
2001
Lernen im neuronalen Netz § 4
Neuronale Netze
Der Lernprozess (es handelt sich um sogenanntes überwachtes Lernen) in unserem Netz geschieht in zwei
Schritten:
• Netzinitialisierung
Sämtliche Gewichte werden als Zufallszahlen vorgegeben
• Trainingsphase
Dem Netz werden Beispieldaten in Form von Aktivitätsmustern der Eingangsneuronen „vorgelegt“ (die
oben erwähnten 7×5-Matrizen – allerdings durch Stapeln der Matrixspalten umgewandelt in Vektoren).
Die Ausgänge werden mit den aktuellen Netzgewichten berechnet. Die Differenzen zwischen den
tatsächlichen Ausgabesignalen yn (aufgrund der Gewichte wi,k und vn,m ) und der gewünschten
Netzreaktion y_solln werden berechnet, quadriert und über alle Trainingsmuster aufsummiert. Dies ergibt
eine Fehlerfunktion
E=
1
∑ ∑ ( y n − y _ solln )2
⋅
2 Muster n
die von allen Netzgewichten wi,k und vn,m abhängt. Sie soll letzten Endes durch das Training möglichst
minimiert werden. Es geht also um die Berechnung des globalen Minimums einer Funktion von „sehr
vielen“ Variablen.
Dazu werden nun sämtliche Gewichte entsprechend einer geeigneten Lernregel so verändert, daß der
Wert der Fehlerfunktion nach der jeweiligen Trainingsrunde kleiner ist als vorher. Die verwendete
Methode ist jene des „steilsten Abstiegs“ auf der Fehlerfläche in Richtung Minimum. Ihre Realisierung
führt auf den sogenannten Backpropagation-Algorithmus, bei dem die Gewichte Schicht für Schicht vom
Ausgang zum Eingang fortschreitend passend korrigiert werden.
Das Training wird mehr oder weniger oft (mindestens einige tausend Mal) durchgeführt mit der Absicht,
den Fehler letzten Endes zu minimieren.
Das „Wissen“ des neuronalen Netzes liegt weitgehend unstrukturiert und gleichmäßig verteilt in seinen
Gewichten.
Und, wohlgemerkt: Das Erkennen eines Musters geschieht über diese antrainierten Fähigkeiten des Netzes
und nicht etwa dadurch, jedesmal das aktuelle Muster mit allen Soll-Mustern zu vergleichen und aus der
Größe der Differenzen das „richtige“ Muster zu berechnen. Anders ausgedrückt: Das ausreichend trainierte
Netz „kennt“ die möglichen Muster und kann die entsprechende Zuordnung immer sofort treffen.
Einige Teile dieses Dokumentes wurden (geändert)
Jörg Kahlert, Fuzzy Control für Ingenieure, Verlag Vieweg
Spektrum der Wissenschaft, November 1992
entnommen.
Robert Salvador
2001