ln(x + 2) - SOS

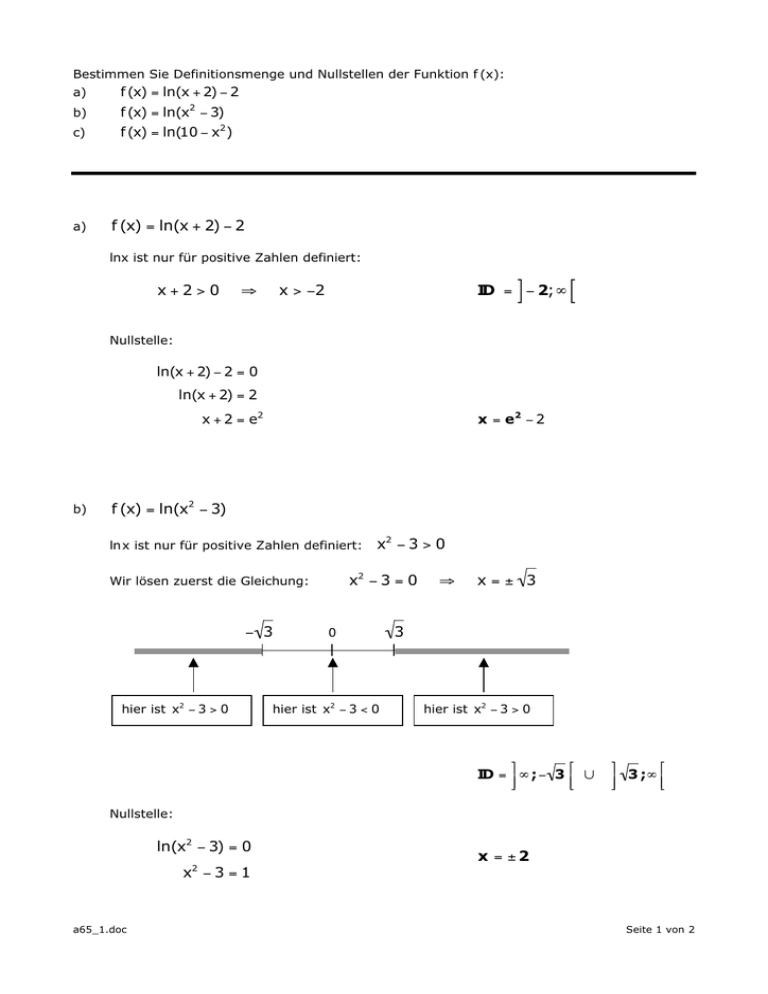
Bestimmen Sie Definitionsmenge und Nullstellen der Funktion f (x):
a)
f (x) = ln(x + 2) − 2
b)
f (x) = ln(x2 − 3)
c)
f (x) = ln(10 − x2 )
a)
f (x) = ln(x + 2) − 2
lnx ist nur für positive Zahlen definiert:
x+2>0
⇒
]
ID = − 2;∞
x > −2
[
Nullstelle:
ln(x + 2) − 2 = 0
ln(x + 2) = 2
x = e2 − 2
x + 2 = e2
b)
f (x) = ln(x2 − 3)
lnx ist nur für positive Zahlen definiert:
x2 − 3 = 0
Wir lösen zuerst die Gleichung:
− 3
hier ist x2 − 3 > 0
x2 − 3 > 0
0
hier ist x2 − 3 < 0
⇒
x=± 3
3
hier ist x2 − 3 > 0
⎤
⎡
ID = ⎥ ∞ ;− 3 ⎢ ∪
⎦
⎣
⎤
⎡
3 ;∞ ⎢
⎦⎥
⎣
Nullstelle:
ln(x2 − 3) = 0
x2 − 3 = 1
a65_1.doc
x = ±2
Seite 1 von 2
c)
f (x) = ln(10 − x2 )
lnx ist nur für positive Zahlen definiert:
Wir lösen zuerst die Gleichung:
− 10
hier ist 10 − x2 < 0
10 − x2 > 0
10 − x2 = 0
0
hier ist 10 − x2 > 0
⇒
x = ± 10
10
hier ist 10 − x2 < 0
⎤
⎡
ID = ⎥ − 10; 10 ⎢
⎦
⎣
Nullstelle:
ln(10 − x2 ) = 0
10 − x = 1
2
a65_1.doc
x = ±3
Seite 2 von 2