Aufgabe 8 – Bit – Darstellung von Zahlen: Mit einer 8 Bit Darstellung

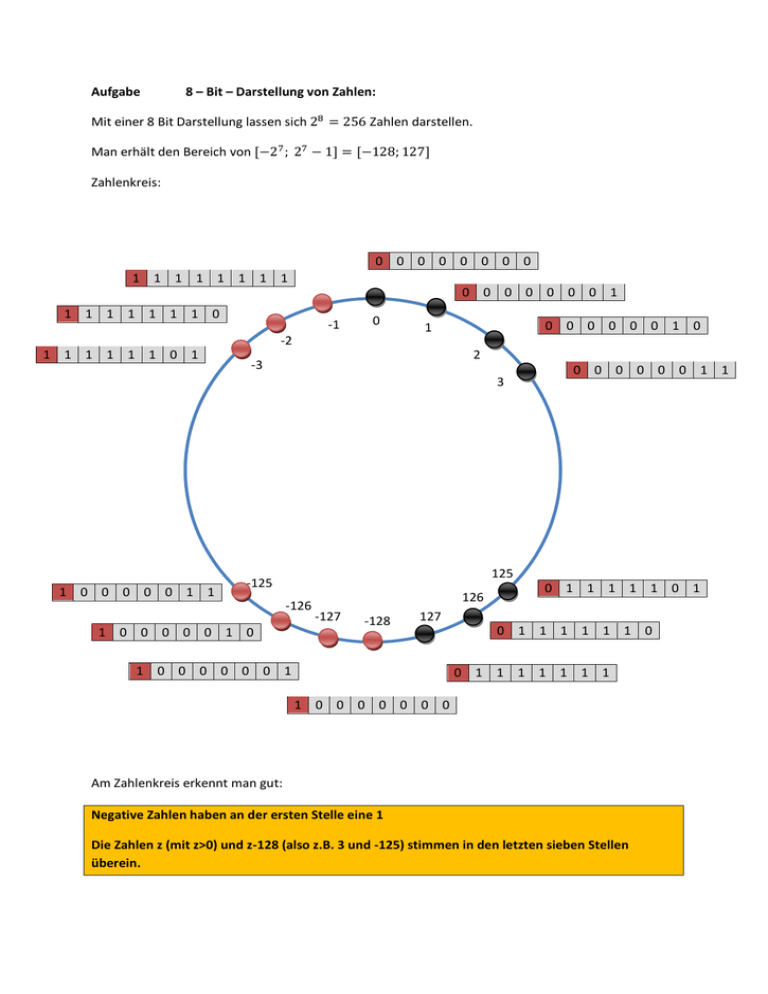
Aufgabe
8 – Bit – Darstellung von Zahlen:
Mit einer 8 Bit Darstellung lassen sich 28 = 256 Zahlen darstellen.
Man erhält den Bereich von [−27 ; 27 − 1] = [−128; 127]
Zahlenkreis:
0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 0
-1
0
-2
1 1 1 1 1 1 0 1
0 0 0 0 0 0 1 0
1
2
-3
3
1 0 0 0 0 0 1 1
0 0 0 0 0 0 1 1
125
-125
-126
1 0 0 0 0 0 1 0
126
-127
-128
0 1 1 1 1 1 0 1
127
1 0 0 0 0 0 0 1
0 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0
Am Zahlenkreis erkennt man gut:
Negative Zahlen haben an der ersten Stelle eine 1
Die Zahlen z (mit z>0) und z-128 (also z.B. 3 und -125) stimmen in den letzten sieben Stellen
überein.
Umrechnung von 125 in das Binärsystem:
125 = 64 + 61 = 64 + 32 + 29 = 64 + 32 + 16 + 13 = 64 + 32 + 16 + 8 + 5 = 64 + 32 + 16 + 8 + 4 +1=
(0 1 1 1 1 1 0 1)2
0 1
64
1
1
1 1 0 1
32
16
8
4
2
1
oder 125 = 127 – 2 am Zahlenkreis ablesen.
Umrechnung von – 2 in das Binärsystem:
Setze in der Zahl 126 das erste Bit auf 1.
1 1 1 1 1 1 1 0
Ergebnis bei einem Überlauf:
127 + 3 = ?
Gehe von 127 um 3 Positionen im Uhrzeigersinn weiter.
Um diese Zahl zu bestimmen, braucht man nur vom arithmetisch korrekten Ergebnis 256 zu
subtrahieren:
130 – 256 = - 126
125 + 10 ergibt somit 135 - 256 = -121
Das Einerkomplement:
Kehrt man jedes Bit einer Zahl um, erhält man das Einerkomplement.
Bsp. (125)10 = (01111101)2
(01111101)2 = (10000010)2 Dies ist die Darstellung der Zahl −126 .
Es gilt:
(𝒛)𝟐 + (𝒛)𝟐 + 𝟏 = 𝟎
Bsp.:
Rechne −𝟏𝟔 in das Binärsystem um:
Weg 1: Rechne 128 − 16 = 112 in das Binärsystem um: 112 = 64 + 32 + 16 = (01110000)2
Setze das erste Bit auf 1: −16 = (11110000)2
Weg 2:
Rechne 16 in das Binärsystem um:
16 = (00010000)2
Bilde das Einerkomplement:
(11101111)2
Addiere 1:
(11110000)2
Weg 3:
Rechne 15 in das Binärsystem um:
15 = (00001111)2
Bilde das Einerkomplement:
(11110000)2