Algorithmen und Datenstrukturen

Was bisher geschah
ADT Menge
Operationen:
I
Suche nach einem Element
I
Einfügen eines Elementes
I
Löschen eines Elementes
Datenstrukturen für ADT Menge
I
lineare Datenstrukturen:
Array, Liste, Hashtabelle
I
hierarchische Datenstrukturen:
Suchbäume, balancierte Suchbäume
144
Priority-Queues
(Vorrang-Warteschlange)
Idee:
I
Modellierung von Prioritäten, z.B. Dringlichkeit
I
Datenstruktur zur Verwaltung von Paaren (Schlüssel, Wert)
I
Schlüssel repräsentieren Priorität
I
kleiner Schlüssel = hohe Priorität
I
Zugriff nur auf ein Element maximaler Priorität (kleinster
Schlüssel)
145
ADT Priority-Queue
I
Sorten: Bool, Element, PQ
I
Signatur:
leer :
PQ →
leerepq :
insert :
PQ × Element →
deletemin :
PQ →
I
Bool
PQ
PQ
PQ × Element
Axiome:
(M(p) bezeichnet die Menge aller in p enthaltenen
Elemente,
min(p) das Element mit geringster Priorität in q)
M(leerepq) = ∅
M(insert(p, e)) = M(p) ∪ {e}
M(deletemin(p)) = (M(p) \ {min(p)}, min(p))
146
Sortieren mit Priority-Queue
Wiederholung: Spezifikation des Sortier-Problemes:
Vorbedingung: Eingabe (x1 , x2 , . . . , xn ) mit
∀i ∈ {1, . . . , n} : xi ∈ natürlicher Zahlen
N
Nachbedingung: Ausgabe (y1 , y2 , . . . , yn ) ist
1. y1 ≤ y2 ≤ · · · ≤ yn+1 (aufsteigend geordnet)
und
2. eine Permutation (Umordnung) der Eingabe
(x1 , x2 , . . . , xn )
Algorithmus zum Sortieren mit Priority-Queue:
1. alle Eingabeelemente x1 , x2 , . . . , xn nacheinander in eine
leere PQ einfügen (insert)
2. alle Elemente nacheinander entfernen und ausgeben
(deletemin)
Laufzeit implementierungsabhängig
147
PQ-Implementierung als Liste
unsortierte Liste:
I
insert: zu Beginn der Liste in O(1)
I
deletemin: Minimum-Suche in O(n)
sortierte Liste:
I
insert: sortiertes Einfügen in O(n)
I
deletemin: O(1)
148
PQ-Implementierung als Baum
Binäre Suchbäume:
Laufzeiten: Tiefe des Baumes
I
insert: sortiertes Einfügen in O(n)
I
deletemin: O(n)
AVL-Bäume:
Laufzeiten: Tiefe des Baumes
I
insert: sortiertes Einfügen in O(log n)
I
deletemin: O(log n)
149
Heaps
Ein Baum t erfüllt die Heap-Eigenschaft:
I
t ist ein vollständig balancierter Binärbaum
d.h. in jedem Knoten Node(x, l, r ) in t gilt:
|size(l) − size(r )| ≤ 1
I
t ist heap-geordnet:
in jedem Knoten Node(x, Node(y , l, r ), Node(z, s, t)) in t
gilt:
x ≤ y und x ≤ z
Beispiele (Tafel)
Auf jedem Pfad eines Heaps sind die Schlüssel sortiert
(aufsteigend von Wurzel zu Blatt)
150
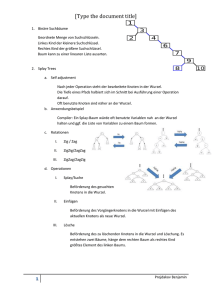
Einfügen eines Schlüssels
Einfügen eines Schlüssels v :
1. Neuen Knoten mit Schlüssel v auf der ersten freien
Position im Heap (Blattebene) einfügen
(ggf. neue Blattebene beginnen)
Heap-Eigenschaft evtl. verletzt
2. benachbarte Knotenwerte entlang des Pfades vom neu
eingefügten Knoten zur Wurzel austauschen, bis Schlüssel
auf dem Pfad sortierte Folge bilden
Warum erhält diese Operation die Heap-Eigenschaft?
Laufzeit: O(log n) (Tiefe des Baumes)
151
Entfernen des Wurzelknotens
Ausgabe und Löschen des Wurzelelementes des Heap:
1. Ausgabe des Wertes in der Wurzel
2. Kopie des Wertes des letzen Blattes in Wurzel, Löschen
des letzten Blattes
Heap-Eigenschaft evtl. verletzt
3. Austausch der Knotenwerte von Vater und dem Sohn mit
kleinstem Knotenwert, beginnend in der Wurzel
Warum erhält diese Operation die Heap-Eigenschaft?
Laufzeit: O(log n) (Tiefe des Baumes)
152
PQ-Implementierung als Heap
Operationen:
I
insert: Einfügen in Heap O(log n)
I
deletemin: Entfernen der Wurzel in O(log n)
153
Heap-Sort
Vorbedingung: Eingabe (x1 , x2 , . . . , xn ) mit
∀i ∈ {1, . . . , n} : xi ∈ natürlicher Zahlen
N
Nachbedingung: Ausgabe (y1 , y2 , . . . , yn ) ist
1. y1 ≤ y2 ≤ · · · ≤ yn+1 (aufsteigend geordnet)
und
2. eine Permutation (Umordnung) der Eingabe
(x1 , x2 , . . . , xn )
Heap-Sort-Algorithmus zum Sortieren:
1. alle Eingabeelemente x1 , x2 , . . . , xn nacheinander in einen
leeren Heap einfügen (insert)
Laufzeit für jedes Element O(log n), gesamt O(n log n)
2. alle Elemente nacheinander entfernen und ausgeben
(deletemin)
Laufzeit für jedes Element O(log n), gesamt O(n log n)
Laufzeit O(n log n)
154