Document

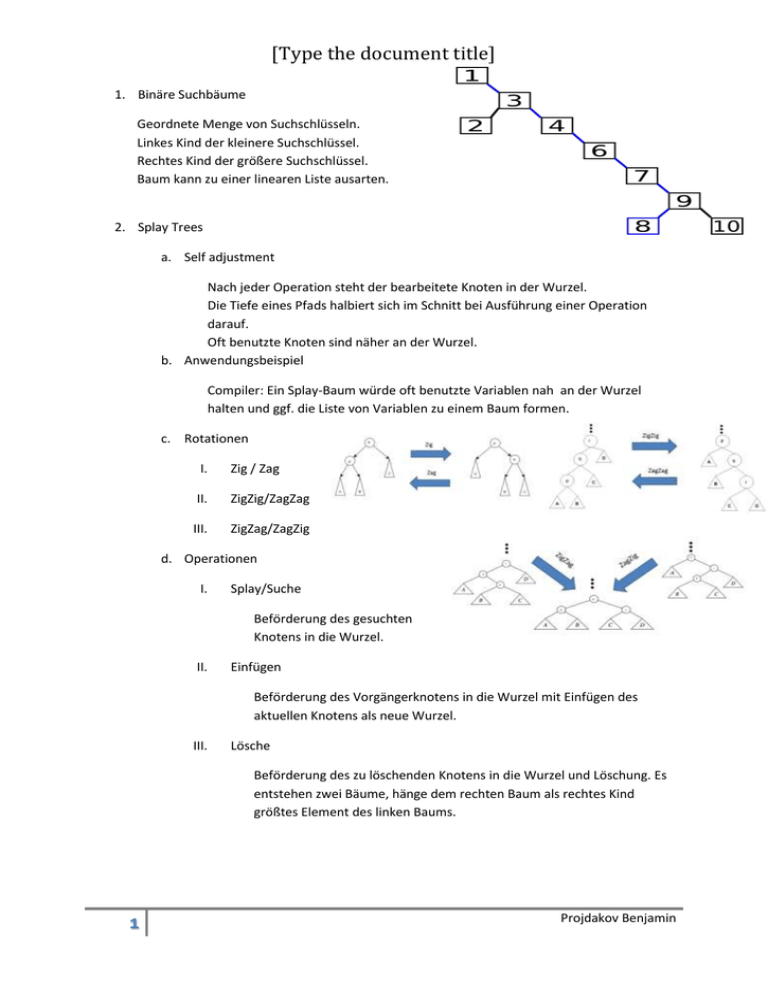
[Type the document title]
1. Binäre Suchbäume
Geordnete Menge von Suchschlüsseln.
Linkes Kind der kleinere Suchschlüssel.
Rechtes Kind der größere Suchschlüssel.
Baum kann zu einer linearen Liste ausarten.
2. Splay Trees
a. Self adjustment
Nach jeder Operation steht der bearbeitete Knoten in der Wurzel.
Die Tiefe eines Pfads halbiert sich im Schnitt bei Ausführung einer Operation
darauf.
Oft benutzte Knoten sind näher an der Wurzel.
b. Anwendungsbeispiel
Compiler: Ein Splay-Baum würde oft benutzte Variablen nah an der Wurzel
halten und ggf. die Liste von Variablen zu einem Baum formen.
c. Rotationen
I.
Zig / Zag
II.
ZigZig/ZagZag
III.
ZigZag/ZagZig
d. Operationen
I.
Splay/Suche
Beförderung des gesuchten
Knotens in die Wurzel.
II.
Einfügen
Beförderung des Vorgängerknotens in die Wurzel mit Einfügen des
aktuellen Knotens als neue Wurzel.
III.
Lösche
Beförderung des zu löschenden Knotens in die Wurzel und Löschung. Es
entstehen zwei Bäume, hänge dem rechten Baum als rechtes Kind
größtes Element des linken Baums.
1
Projdakov Benjamin
[Type the document title]
3. Amortisierte Analyse
a. Einführung/Potenti al-Methode:
Verrechne tatsächliche Kosten mit Strukturveränderung zu Ausgleichskosten.
𝑎𝑜𝑝 = 𝑡𝑜𝑝 + 𝜙𝑛𝑜𝑤 − 𝜙𝑏𝑒𝑓𝑜𝑟𝑒
b. Hilfssatz
Bedingt (𝑎, 𝑏 > 0, 𝑎 + 𝑏 ≤ 𝑐) Abschätzung der Summe zweier Logarithmen.
√𝑎𝑏 ≤
𝑎+𝑏
2
log 2 𝑎 + log 2 𝑏 ≤ 2 log 2 𝑐 − 2
c. Definitionen
Einführung der Komponenten des Modells:
Rang von p: 𝑟(𝑝) = log 2 𝑠(𝑝)
Potential von b: 𝜙(𝑏) = ∑𝑟(𝑝)
Größe von p : 𝑠(𝑝) = ∑𝑤(𝑥)
Gewicht von x : 𝑤(𝑥) > 0
d. Zugriffslemma
Jede Splay-Operation hat als amortisierte Laufzeit maximal:
3(𝑟(𝑏) − 𝑟(𝑥)) + 1
Ableitung von Regeln aus den Zustandsänderungen.
I.
II.
III.
2
Zig/Zag
ZigZag/ZagZig
ZigZig/ZagZag
Projdakov Benjamin
[Type the document title]
IV.
Splay
Treppensumme von :
= 3
( ( ) ( ))
𝑟
𝑏
− 𝑟
𝑥
+ 1
e. Satz 1: Splay-Baum
Amortisiere Laufzeit für Splay-Bäume.
„Für einen anfangs leeren Baum benötigt das Ausführen von m Wörterbuchoperationen mit höchsten N Einfüge-Operationen maximal O(m log N).“
Wörterbuchoperationen brauchen eine konstante Anzahl von Splay-Operationen
+ eine konstante Anzahl Einzeloperationen.
Für diesen Beweis setzen wir alle Gewichte auf 1 .
Laufzeit:
𝑎𝑠𝑝𝑙𝑎𝑦 ∈ 𝑂(log(𝑁))
⇒ 𝑚 𝑂𝑝𝑒𝑟𝑎𝑡𝑖𝑜𝑛𝑒𝑛 ∈ 𝑂(m log(𝑁))
f.
Satz 2: Binärer Baum mit Splay
Laufzeit auf Suchbäumen
„Für einen binären Suchbaum mit N Knoten, haben m Suchoperationen (über
Splay) einen Aufwand von maximal O((N + m) log (N) + m).“
Eine Suchoperation besteht aus einer Splay-Operation und Rückgabe des
neuen Wurzelknotens.
3
Projdakov Benjamin
[Type the document title]
Für diesen Beweis setzen wir alle Gewichte auf 1 .
Wir suchen die tatsächlichen Kosten, über:
𝑡𝑜𝑝 = 𝑎𝑜𝑝 + 𝜙𝑏𝑒𝑓𝑜𝑟𝑒 − 𝜙𝑛𝑜𝑤
Laufzeit: ∈ 𝑂((𝑚 + 𝑁) log 2 𝑁 + 𝑚)
4
Projdakov Benjamin