1 reelle zahlen

Brückenkurs Mathematik
Teil I.1
Rechnen mit reellen Zahlen
Inhalt
1 Reelle Zahlen
1.1 Zahlbereiche
1.2 Grundrechenarten
1.3 Potenz- und Wurzelrechnung
1.4 Logarithmen
Staatliche Studienakademie Leipzig
Studienrichtung Informatik
Dr. Christian Heller
12. September 2011
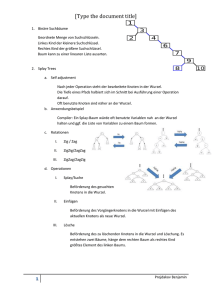
Zahlbereiche
Grundrechenarten: Stufen (Klassen)
X
^
1. Stufe:
Addition, Subtraktion
2. Stufe:
Multiplikation, Division
3. Stufe:
Potenz-, Wurzel- und Logarithmenrechnung
Menge der natürlichen Zahlen 2 { X
Menge der ganzen Zahlen
‚2 { ^
1
Menge der rationalen Zahlen
{ Z
Z
3
\ „ Z Irrationale Zahlen
Ƴ
\
Menge der reellen Zahlen
Ɓ2 { \
Menge der komplexen Zahlen 1Ÿi { Q
Q
Punktrechnung vor Strichrechnung!
Grundrechenarten: Gesetze
Addition
Kommutativgesetze aŸb bŸa
Assoziativgesetze
Klammerausdrücke
Multiplikation
a‚ƎbŸc Ə a‚b‚c
a·b b·a
aƎbŸc Ə abŸac
aŸƎbŸcƏ ƎaŸbƏŸc a·Ǝb·cƏ Ǝa·bƏ·c
a‚Ǝb‚cƏ a‚bŸc
ƎaŸbƏƎcŸdƏ acŸadŸbcŸbd ƎaŸbƏƎc‚d Ə ac‚adŸbc‚bd
Ǝa‚bƏƎcŸdƏ acŸad‚bc‚bd Ǝa‚bƏƎc‚d Ə ac‚ad‚bcŸbd
Distributivgesetz
a·ƎbŸcƏ a·bŸa·c
ſ gilt für beide
a ,b , c { \
Bruch: Rechenregeln
Addition :
a c
adŸbc
Ÿ b d
bd
Subtraktion
ad‚bc
a c
‚ b d
bd
Binomische Formeln (Spezialfälle):
1.
2.
3.
ƎaŸbƏ2 ƎaŸbƏƎaŸbƏƎaŸbƏ a 2Ÿ2abŸb2
2
2
2
Ǝa‚bƏ Ǝa‚bƏƎa‚bƏ a ‚2abŸb
ƎaŸbƏƎa‚bƏ a 2‚b2
Betrag
Als Betrag | r | einer reellen Zahl r wird der Abstand dieser
Zahl r vom Nullpunkt 0 erklärt.
Multiplikation
ac
a c
· b d
bd
Division
a
b
a d ac
+ d
b c bd
c
‹r‹ a ,b , c , d { ^
b,d Ÿ 0
‚rr fürfür rr ¢Ź 00
(d.h. r ist positiv oder gleich 0)
(d.h. r ist negativ)
Partialdivision und Polynomdivision
1 Ordnen von Dividend und Divisor
ì
Das Potenzieren ist wie das Multiplizieren seinem
ordne alphabetisch und dann nach fallenden Potenzen
2 Ausführen der Partialdivision
ì
Potenz: Definition
Ursprung nach eine abkürzende Schreibweise für eine
wiederholte mathematische Rechenoperation.
dividiere ersten Summanden des Dividenden durch den
ersten Summanden des Divisors
Wie beim Multiplizieren ein Summand wiederholt addiert
wird, so wird beim Potenzieren ein Faktor wiederholt
ì
multipliziere Quotienten mit ganzem Divisor
ì
subtrahiere entstehendes Produkt vom Dividenden
ì
(ordne Ausdruck eventuell neu)
ì
rechne weiter mit entstandenem Rest, bis Division
aufgeht oder nicht teilbarer Rest bleibt
Potenz: Beispiele
multipliziert.
mit :
a { \
n ź 1
n { X
a Ŷ
a·a·...·a
n
n Faktoren a
Potenz: Gesetze
a ·a a
m
n
m
0 0 Ǝv nŸ0Ə
a 1 ƎaŸ0Ə
Basen gleich:
a a
1
a n ƎaŸ0Ə
a
Exponenten gleich : an·b n ƎabƏn
n
1
0
‚n
Zusätzlich :
a: Basis
n: Exponent
a
m‚n 1
a n‚m
n
a
a
mŸn
ƎƏ
an a
n
b
b
n
ƎbŸ0Ə
Ǝ am Ə am·n Ǝ an Ə
n
mit ganzzahligen Exponenten :
a ,b { \
a ,b Ÿ 0
m,n { ^
m
mit reellen Exponenten:
a ,b { \
a ,b ź 0
m,n { \
Wurzel: Definition
Wurzel: Beispiele
Die n-te Wurzel für n=1, 2, … aus einer nichtnegativen
reellen Zahl a ist diejenige nichtnegative reelle Zahl b, für
n
n
a a Ɓ11
Ɓ
n
n
00
Ɓ
die bn=a gilt.
1
aa
Ɓ
Das Radizieren bzw. Wurzel Ziehen stellt eine Umkehrung
Durch die beiden folgenden Umwandlungen können die
des Potenzierens dar.
Wurzelgesetze auch als Potenzgesetze für gebrochene
a: Radikant
n: Wurzelexponent
b: Wurzelwert bzw. Radix bzw. n-te Wurzel aus a
Ɓab o ab
n
Exponenten geschrieben werden.
mit :
a ¢ 0
b ¢ 0
n { X
n
Ɓaa
n
Wurzel: Gesetze
Radikant gleich :
Ɓa·Ɓa
m
n
ƁamŸn
n
n
n
a·Ɓb Ɓab
Ɓ
Zusätzlich :
Ɓa
n
m
m
n
Ɓa mnƁam‚n
n
Ɓa
m
a
mit :
a ,b ¢ 0
n { X
m { ^
m
n
Die Potenzgesetze gelten nicht für das Wurzel Ziehen aus
m
negativen Radikanten!
Ɓ
Ɓ
Ɓa n a Ǝbź0Ə 1 n 1
n
n
Ɓb b
Ɓb b
n
a Ǝ Ɓa Ə
n
Ɓa
n
Wurzel: aus negativen Radikanten
mn
Exponent gleich :
1
n
m
Ɓn am npƁamp
Allgemein gilt :
ƁƁa ƁaƁƁa
m n
mn
Ɓa2m
2m
n m
mit :
a ,b { \
a ,b ¢ 0
m,n { X
‹a‹
Für ungeradzahlige Wurzelexponenten n2m‚1 gilt :
2n‚1
2n‚1
Ɓ‚a ‚ Ɓa
Für geradzahlige Wurzelexponenten n2m existiert die
Wurzel für negative Radikanten zwar nicht im Bereich der
reellen Zahlen \ , aber in jenem der komplexen Zahlen Q .
Logarithmus: Definition
Logarithmus: Beispiele
Unter dem Logarithmus einer positiven reellen Zahl b zu
einer positiven, von eins verschiedenen reellen Basis a
versteht man diejenige reelle Zahl c, mit der die Basis a zu
a
log a b
b
loga Ǝa Əb
b
log a 10 loga a1
log 1 a Ǝnicht erklärt Ə
potenzieren ist, um b zu erhalten.
Der Logarithmus stellt die (neben der Wurzel) zweite
Umkehrung der Potenz dar.
mit :
a ,b , c { \
a ź 0
a Ÿ 1
b ź 0
log a bc o bac
Logarithmus: Gesetze
log a a1
log 10
a
log ƎabƏlog aŸlog b log log a‚log b ƎbŸ0Ə
b
log a n·log a
n
1
n
log Ɓa ·log a
n
gültig für Logarithmen
beliebiger Basen
dekadisch: xlg b o b10
y
natürlich : yln b o be
z
dual :
zld b o b2
x