Übungen

Übungen
Lineare Gleichungs– und Ungleichungssysteme 1
1.
Welche Zahlenpaare sind Lösungen der Gleichung 7x–4y = 3?
a) (1/1)
2.
b) (3/4)
4.
b) (?/2)
6.
c) (3/?)
d) (?/–2)
Zeichnen Sie in einem x–y–Koordinatensystem die Geraden, die zu den Gleichungen gehören.
a) y = 0.5x–1
b) 2y–x = 2
c) x–3y = –1
e) 5x–20y+16 = 0
f) 0 = 4x–10y–5
g) 15–4x = 6y
d) 3x = 2–4y
Veranschaulichen Sie die Lösungsmenge der Ungleichungen.
a) y ≤ 2x–1
5.
d) (0/–0.75)
Ergänzen Sie die fehlende Zahl, sodass sich eine Lösung der Gleichung x–0.5y = 1 ergibt.
a) (0/?)
3.
c) (–2/–4)
b) y > –0.75x+2
c) x–3y < 12
d) x+y–1 ≥ 0
Veranschaulichen Sie die Lösungsmenge der Gleichungen in einem x–y–Koordinatensystem.
a) y = 2
b) 3y = 4
c) x = –2
d) 5x = 2
e) 3y < 5
f) 4 ≥ –2y
g) 5x < 3
h) –2x > 1
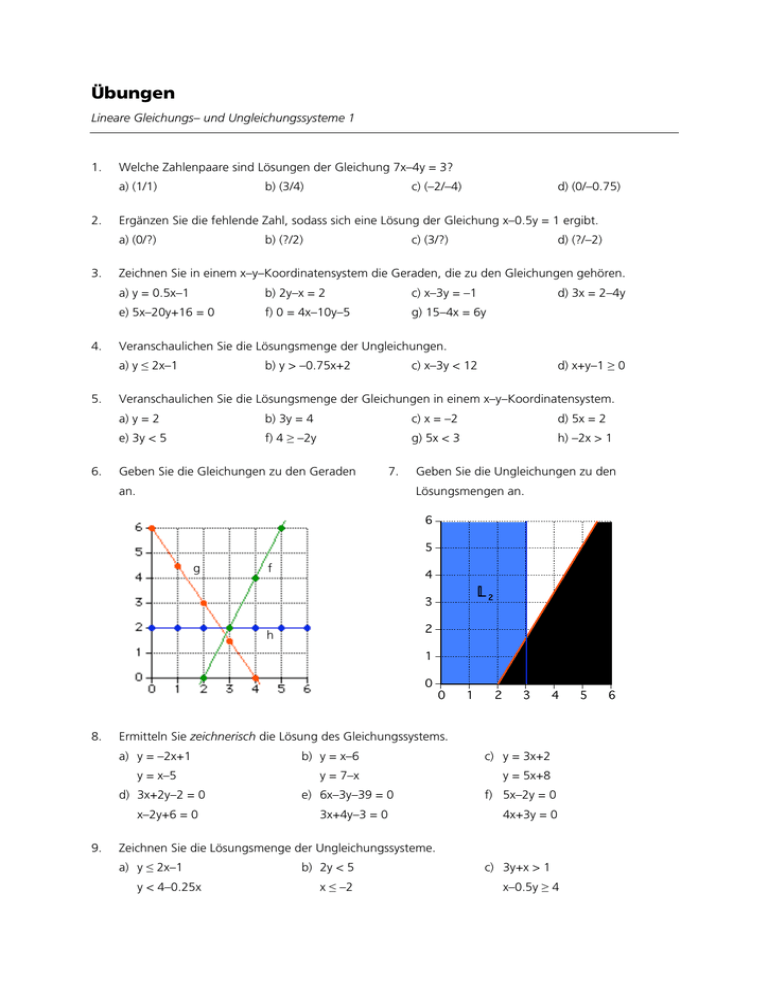
Geben Sie die Gleichungen zu den Geraden
7.
an.
Geben Sie die Ungleichungen zu den
Lösungsmengen an.
6
5
g
f
4
ø2
3
ø1
2
h
1
0
8.
1
2
3
4
Ermitteln Sie zeichnerisch die Lösung des Gleichungssystems.
a) y = –2x+1
y = x–5
d) 3x+2y–2 = 0
x–2y+6 = 0
9.
0
b) y = x–6
c) y = 3x+2
y = 7–x
y = 5x+8
e) 6x–3y–39 = 0
3x+4y–3 = 0
f) 5x–2y = 0
4x+3y = 0
Zeichnen Sie die Lösungsmenge der Ungleichungssysteme.
a) y ≤ 2x–1
y < 4–0.25x
b) 2y < 5
x ≤ –2
c) 3y+x > 1
x–0.5y ≥ 4
5
6
10. Ermitteln Sie zeichnerisch alle Paare ganzer Zahlen, welche Lösungen des Systems sind.
a) y ≥ 3
b) y ≤ x
c) y > 1+x
2y < 16–x
6y > 6+x
3y+x+3 > 0
y ≤ x–4
3y+x < 12
2y = 4+x
11. Bestimmen Sie die Lösungsmenge. Verwenden Sie dazu das Additionsverfahren.
a) x+y = 26
b) –x+5y = 4
x–y = 8
d) 8x–7y = 38
x–2y = 5
e) 9x–2y = 4
3x–7y = 23
g) 8x–7y = 1
c) 4x–7y+34 = 0
2x+7y–4 = 0
f) 4x+9y = 15
11x+y = 29
h) 9x+5y = 2
–2x+3y = 11
2x–7y = 19
i) 9x+7y = 8
12x+7y = 4
j) 28u–23v = 13
k) 11s–75t = 0
21u+8v = –66
9s–100t = 0
15x+11y = 13
l) 2.25x–7y = 1
0.75x–2y = 0.5
12. Bestimmen Sie die Lösungsmenge. Verwenden Sie das Einsetzungsverfahren.
a) x+3y = 3
b) 6x+5y = 65
y = 3x
d) 5x–7y+9 = 0
5x+6 = 56
4x = –5y
e) x–2y = 9
f) 3x–4y = 9
x = 3y+5
2x = 4y+2
x+y = 0
g) 8x+15y = 39
c) 8x+11y = 12
h) 9(x–y)+24x = 100
15y = 2x+9
i) x = 10y–27
3(x–y) = 32
x = 4y+27
13. Bestimmen Sie die Lösungsmenge. Wählen Sie selbst einen Lösungsweg!
a) 4y–19 = y+ 20
b) 20x–50 = 29y
5x+2y = 126
2x+5y = 8y
d) x = 8y–6
e) y = 2x–3y+4
x = 3y+4
x = 2x–3y+4
g)
25x- 3 20y-1
= 2x- y
12
18
x+ 4 y+ 3
=
9
5
c) 3x+50 = 6x+5y
h)
x+ y 4y
+
= 10
2
3
5- y =
2y+10 = 3x+2y
f) 3(2y+3) = 2x+7y
4(x+2) = 5x–3y
i)
x+ y
2
7(x- y) x
+ = 4.8
11
4
7(x- y) 3x
= 2.4
11
4
Lösungen
1a) ja, b) nein, c) nein, d) ja. 2a) –2, b) 2, c) 4, d) 0.
3a) y = 0.5x–1, b) y = 0.5x+1; c) y = 1/3·x+1/3, d) y = –0.75x+0.5, e) y = 0.25x+0.8, f) y = 0.4x–0.5, g) y = –2/3·x+5/2.
4a) y ≤ 2x–1, b) y > –0.75x+2, c) y > 1/3·x–4, d) y ≥ –x+1.
5a) y = 2, b) y = 4/3, c) x = –2, d) x = 2/5, e) y < 5/3, f) y ≥ –2, g) x < 3/5, h) x < –0.5.
6) f: y = 2x–4, g: y = –1.5x+6, h: y = 2. 7) L1 = {(x/y)| y≤5/3·x–10/3}, L2 = {(x/y)| x<3}.
8a) (2/–3), b) (6.5/0.5), c) (–3/–7), d) (–1/2.5), e) (5/–3), f) (0/0). 10a) (7/3)…(9/3), b) (2/2)…(5/2), c) (–2/1), (0/2).
11a) (17/9), b) (11/3), c) (–5/2), d) (3/–2), e) (2/7), f) (6/–1), g) (8/9), h) (–2/4), i) (0.5/0.5), j) (–2/–3), k) (0/0), l) (2/0.5).
12a) (0.3/0.9), b) (10/1), c) (–15/12), d) (–0.75/0.75), e) (17/4), f) (7/3), g) (3/1), h) (1/6 /–10.5), i) (63/9).
13a) (20/13), b) (75/50), c) (10/3 /8), d) (10/2), e) (2/2), f) (5/–1), g) (5/2), h) (–35/15), i) (2.4/–4.2).
Übungen
Lineare Gleichungssysteme 2: Textaufgaben
1.
a) Suchen Sie zwei Zahlen, deren Summe 34 und deren Differenz 16 ist.
b) Eine Zahl ist um 8 grösser als eine andere, aber nur halb so gross wie deren Dreifaches. Um
welche beiden Zahlen handelt es sich?
c) Gibt es zwei natürliche Zahlen mit dem Mittelwert 17, von denen die eine doppelt so gross ist wie
die andere.
2.
Die Summe zweier gesuchter Zahlen ist zehnmal so gross wie ihre Differenz, die Summe ihrer reziproken Werte aber zehnmal so gross wie das Produkt ihrer reziproken Werte.
3.
Zwei Ziffern bilden eine natürliche Zahl, die viermal so gross ist wie ihre Quersumme und um 9 kleiner als ihre Spiegelzahl. Bestimmen Sie die Zahl!
4.
Vor 5 Jahren war der Vater 5mal so alt wie der Sohn. In 3 Jahren wird er 3mal so alt sein wie der
Sohn. Wie alt sind die beiden jetzt?
5.
Marie ist jetzt 24 Jahre alt, doppelt so alt wie Anna war, als Marie so alt war, wie Anna jetzt ist. Wie
alt ist Anna jetzt und wann war Marie gerade so alt?
6.
An einer Tombola kostet ein blaues Los Fr. 3.–, ein rotes, mit der 4fachen Gewinnchance, Fr 10.–.
Am Nachmittag werden für diese Lose Fr 278.– eingenommen. Am abend werden 51 blaue Lose
weniger verkauft, dafür aber 49 mehr von den roten. Damit ergaben sich an diesem Tag aus der
Tombola Einnahmen von Fr 893.–. Wie viele rote und blaue Lose wurden am Nachmittag verkauft?
7.
Ein Kapital wird zu 4% verzinst, ein anderes zu 5%. Dies Summe der beiden Jahreszinsen beträgt
Fr 1410.–. Wird nach einem Jahr jeder Zins zu seinem Kapital geschlagen, so werden die beiden Kapitalien gleich gross. Wie gross waren sie am Anfang?
8.
Ein Kaufmann mischt zwei Kaffeesorten. Nimmt er von der billigeren Sorte doppelt so viel wie von
der teuren, so kommt das Kilo auf Fr 17.10 zu stehen, im umgekehrten Fall auf Fr 18.50. Berechnen
Sie die Kilopreise der beiden Sorten.
9.
Zwei Radfahrer fahren auf einer 400 m langen Rennbahn mit praktisch konstanten Geschwindigkeiten. Der zweite startet 10 Sekunden nach dem ersten, 45 Sekunden später holt er ihn zum ersten
Mal ein und weitere 225 Sekunden später zum zweiten Mal. Wie schnell fahren die beiden?
10. In ein 10 m langes und 5 m breites quaderförmiges Wasserbecken münden zwei Zuleitungen. Sind
beide während einer Stunde geöffnet, so steigt der Wasserspiegel um 1.08 m. ist aber die erste nur
50 min lang geöffnet und die zweite dafür 70 min lang, so steigt er um 1.05 m. Wie viele Liter liefert
jede Leitung pro Minute?
Lösungen
1a) 9, 25, b) 16, 24, c) nein. 2) 4.5, 5.5. 3) 12. 4) 13 J. und 45 J. 5) Anna ist 18 J.
6) mehrere Lösungen z.B. 56 blaue, 11 rote Lose. 7) Fr 15'750.– und Fr 15'600.–. 8) Fr 15.70 und Fr 19.90.
9) 8 m/s und 9.8 m/s. 10) 375 l/min und 525 l/min.
Übungen
Lineare Gleichungssysteme 3: Drei Variablen, Lösbarkeit
1.
Bestimmen Sie die Lösungsmenge.
a) x+y+z = 9
c) x+4y–5z = 21
x–y+z = 3
2x–y+z = 8
2x+3y+4z = –1
x+y–z = 1
3x+2y–z = 20
x–6y–8z = –3
d) 2x+3y+4z = 1.4
e) z = 3x–4y–2
f) x+y+z = 14
3x–2y–z = 1.2
z = 2x+3y–13
2x = 5z
5x+4y+3z = 1.4
z = 5x–9y+2
6y = 7z
g) x+y = 11
h) 2.4x–2.5y = 26
x+z = 12
1.6x+0.9z = –3
4x–(5–6y) = 8z–3
y+z = 13
0.5y–1.2z = 38
9y–(x+2z) = 2
j) 2x+3(y–z) = 2
2.
b) x+y–z = 7
k) 3(x–6)–4(y+z) = –18
i) 2x–(3y+4z) = –1
l) 3r–4s+2t = 10
3(y+x)–2(z+x) = 4
5x–8(z+2y) = 0
5r–3s+4t = 3
5(y–z)–3(x–y) = –42
4(y+z)–5(x–1) = 5
–2r+5s–3t = –7
a) Suchen Sie drei Zahlen, sodass sich die Summen 10 bzw. 11 bzw. 12 ergeben, wenn man je zwei
von ihnen addiert.
b) Bei drei Zahlen x, y und z kann man von jeweils zweien den Mittelwert bilden. Ist es möglich, dass
sich dabei jedesmal der Wert 10 ergibt, obwohl die drei Zahlen x, y und z verschieden sind?
3.
Ermitteln Sie die vierstellige Zahl mit folgenden Eigenschaften:
Die Quersumme beträgt 14.
Die Summe von Tausender- und Einerziffer ist gleich der Summe von Hunderter- und Zehnerziffer.
Die Summe von Tausender- und Hunderterziffer ist gleich der Summe von Zehner- und Einerziffer.
Die Tausenderziffer ist um 1 grösser als die Einerziffer.
4.
a) Bestimmen Sie die Steigung und den y–Achsenabschnitt der Geraden, die durch die Punkte P(1/2)
und Q(5/4) geht.
b) Bestimmen Sie die Parameter a, b und c der Kurve y = ax2 + bx + c, die durch die Punkte P(1/3),
Q(2/4) und R(–1/–5) geht. Zeichnen Sie die Kurve!
5.
Eine Bergbahn verlangt für Berg- und Talfahrt zusammen Fr 30.–, für die Bergfahrt allein Fr 22.50
und für die Talfahrt allein Fr 15.–. An einem Sonntag fuhren im ganzen 680 Zahlende hinauf und
520 hinab. Es wurden Fr 19'650.– eingenommen. Wie viele Billette jeder Art wurden gelöst?
6.
Ein Wasserbehälter kann durch drei Zuleitungen gefüllt werden, und zwar durch A und B zusammen
in 60, durch A und C zusammen in 45 und durch B und C zusammen in 36 Minuten. In wie vielen
Minuten wird der Behälter durch jede Leitung einzeln gefüllt, in wie vielen durch alle drei
gemeinsam?
7.
Ein Radfahrer hat eine Geschwindigkeit von 25 km/h auf ebenem Gelände, von 15 km/h bergaufwärts und von 30 km/h abwärts. Wieviel ebenen, ansteigenden und absteigenden Weg enthält
unter diesen Voraussetzungen eine 100 km lange Strasse, wenn der Radfahrer 4 h 24 min braucht
um sie in der einen Richtung, und 4 h 36 min, um sie in der anderen Richtung zu durchfahren?
8.
Bestimmen Sie die Lösungsmenge.
a) 3y = 2x+3
y+1 =
b) 0.8x+y = 0.6
2x
3
d) 4x–3(1–y) = 2(x–y)
e) 5(4y–3x) = 4x–5y
x y 2
+ =
2 3 3
x y 1
- =
2 3 6
0.2x+0.25y = 0.15
x–(–y–x+1) = 6–4y
9.
c)
f) 1–2(y–2x) = 2(1+x)–(1+2y)
3(2x–y) = 2(x+1)–(2+3y–4x)
4(y+2x) = 3(x–y)+(5x+7y)
Überprüfen Sie anhand einer Zeichnung, ob das System ein, keine oder unendlich viele Lösungen hat.
a) y = x–2
b) x–y+3 = 0
c) x–2y = 5
y = 0.5x – 0.5
2y = 8+x
2x–y = 1
y = –0.5x+2.5
x+2y = 10
0.5x = 2.5+y
10. Bestimmen Sie die Zahl der Lösungen.
a) x+y–z = 1
b) x–y+2z = –2
c) 2x–3y+z = 0
x+3y = 3
3x–y+5z = –5
x–4y–2z = 1
2x+4y–z = 7
2x–4y+5z = –5
3x–2y+4z = 13
11. Lösen Sie die Aufgaben mit dem Taschenrechner.
a) 19x–4y+4z = 5
b) 12x–(5y+8z) = 3
c)
2x + 3x - z = 5
5x–12y–10z = –3
3y = 4x+9z
2x + y + 3z = - 5
–15x+8y+3z = 4
5x+17 = 4y–2z
3x - 5z = 0
d) 123x+234y = 100
e) 5x+2y = 8
245x+467y = –200
10x+4y = 16
f) 12x+16y–8z = 7
7x+12y–16z = 8
3x+4y–2z = 9
Lösungen
1a) (2/3/4), b) (5/3/1), c) (–1/3/–2), d) (0.3/–0.4/0.5), e) (3/2/–1), f) (7.5/3.5/3), g) (5/6/7), h) (15/4/–30),
i) (1/2 / 1/3 / 1/4), j) (10/6/12), k) (0/0/0), l) (2/–3/–4). 2a) 4.5, 5.5, 6.5, b) nein.
3) 4343. 4a) y = 0.5x+1.5, b) y = –x2+4x+0. 5) 460 B&T, 220 B, 60 T. 6) 180 min, 90 min, 60 min, gemeinsam 30 min.
7) 50 km eben, 22 km ansteigend, 28 km abfallend. 8a) L = {}, b) L = {(x/y)| y=–0.8x+0.6}, c) (5/6 / 3/4), d) L = {},
e) {(x/y)| 25y–19x=0}, f) L = {(x/y)| x=0}. 9a) (3/1), b) L = {}, c) (–1/–3). 10a) L = {}, b) unendlich viele Lösungen, c) L = {}.
11a) (–1.6667/–4.4091/4.7576), b) (6.9016/13.6120/1.4700), c) (–1.1478/1.8367/–1.1448), d) (842.34/–442.34),
e) unendlich viele Lösungen, f) keine Lösung.
Übungen
Lineare Gleichungssysteme 4: Zusätzliche Textaufgaben
1.
Eine dreistellige natürliche Zahl hat die Quersumme 18. Vertauscht man die erste Ziffer von links mit
der zweiten, so wächst die Zahl um 180; vertauscht man statt dessen die zweite Ziffer mit der
dritten, so wächst die Zahl um 18.
Wie heisst die Zahl?
2.
Der Mittelwert zweier dreistelliger natürlicher Zahlen, die sich nur in der Reihenfolge der zwei ersten
Ziffern unterschieden, beträgt 555. Teilt man jede der beiden Zahlen durch ihre Quersumme, so
ergibt sich 49 resp. 25.
Um welche beiden Zahlen handelt es sich?
3.
Ein Kapital von Fr 330'740.– ist in drei Posten zu 4%, 5% und 6% angelegt. Schlägt man nach
einem Jahr die Zinsen dazu, so werden alle Posten gleich gross.
Wie gross waren die Posten am Anfang?
4.
Von einem Dreieck sind die Seitenlängen a, b und c gegeben.
In welchen Abständen von den Ecken berührt der Inkreis die Seiten?
5.
Ein Kuind trägt eine Anzahl Fünf-, Zwei- und Einfrankenstücke lose in seiner Hosentasche. Es verliert
von jeder Sorte ein Stück und besitzt dann wertmässig noch so viele Franken, als es am Anfang
Geldstücke in der Tasche hatte.
Wie viele Stücke jeder Sorte hatte es anfangs bei sich?
Lösungen:
1) 468. 2) 735, 375. 3) Fr 111'300, Fr 110'240, Fr 109'200. 4) (–a+b+c)/2, (a–b+c)/2, (a+b–c)/c.
5) 1x Fr 5, 4x Fr 2, mind 1x Fr 1.