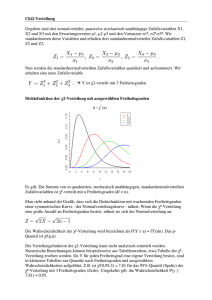
Erklärung zur t
Werbung

t-Verteilung Gegeben sind eine standardnormalverteilte Zufallsvariable (Z1) sowie die F-Verteilung des vorangegangenen Beispiels. Der Quotient ist t-verteilt mit 4 Freiheitsgraden. Der Quotient aus einer standardnormalverteilten Zufallsvariablen und der Wurzel einer χ2verteilten Zufallsvariablen mit n Freiheitsgraden, geteilt durch ihre Freiheitsgrade, ist tverteilt mit n Freiheitsgraden. Die Wahrscheinlichkeit wird bezeichnet als P(t ≤ a) = ft(a|n). Das p-Quantil ist t(p;n). Die Dichtefunktion der t-Verteilung ist, ähnlich wie die der Standardnormalverteilung, symmetrisch bezüglich des Erwartungswertes 0. Es gilt daher für die Berechnung der Verteilungswerte: a∈R Auch die t-Verteilung ist meistens nach Freiheitsgraden und ausgewählten Quantilen tabelliert. Mit zunehmender Anzahl an Freiheitsgraden nähert sich die t-Verteilung an die Normalverteilung an, d.h. für großes df gilt: